超声速欠膨胀喷流噪声数值模拟研究

施方成，王田天

湖南大学，湖南 长沙 410082

战斗机、火箭等空天飞行器发动机射出超声速喷流，其伴随产生的高强度噪声可在飞行器表面产生巨大的声负载[1-3]，引起结构或有效载荷出现声疲劳失效[4]。因此，超声速喷流噪声的机理研究与降噪设计日益受到学术界与工业界的关注[5-8]。而在大空域飞行的情况下，战斗机、火箭等飞行器的发动机喷嘴极易处于非设计状态[9]。因此，针对超声速非理想膨胀喷流噪声的研究具有一定的应用价值。

超声速非理想膨胀喷流噪声可分为湍流噪声和激波相关噪声，前者包括大尺度湍流噪声和小尺度湍流噪声，后者包括宽频激波噪声和啸音[10]。相比湍流噪声，激波相关噪声的声源涉及激波/湍流相互作用，产生机理更为复杂。本文重点关注激波相关噪声中的宽频激波噪声，其最早在D.L.Martlew 的试验中被观测到[11]。M.Harper-Bourne 和M.J.Fisher[12]提出宽频激波噪声是由喷流剪切层中湍流与激波波系相互作用所诱导产生的。之后，美国国家航空航天局（NASA）兰利研究中心J.M.Seiner 等[13-16]针对宽频激波噪声开展了一系列的试验研究，验证了“宽频激波噪声产生于激波和剪切层相互作用处”的观点，并提出宽频激波噪声的多普勒效应由对流输运效应引起[15]，而非Harper-Bourne等主张的声源相位差。此外，J.M.Seiner和J.C.Yu[16]基于试验观察指出大尺度湍流相干结构与激波单元相互作用是产生宽频激波噪声的主导因素。基于此，C.K.M.Tam 和H.K.Tanna[17]建立了新的峰值频率和声强预估模型，该模型在参考文献[18]中得到了进一步发展。

虽然前述模型取得了一定的成功，但通过理论和试验手段研究欠膨胀喷流中激波/湍流相互作用和宽频激波噪声产生机理存在局限性。近年来，数值模拟技术的发展促进了相关的研究工作。D.Rotman[19]根据二维正激波/各向同性湍流相互作用的数值模拟发现激波后湍动能增大现象，之后斯坦福湍流研究中心Lele 课题组和其他团队将其研究推广至三维流动，详细研究了雷诺应力分量[20-21]、湍流涡量[22-23]、热力学脉动量[24]以及湍流尺度[21-25]过激波的变化过程。Shi Fangcheng 等[26]讨论了正激波/各向同性湍流相互作用对激波后湍流辐射噪声能力的影响及其物理机制。为了更合理地反映非理想膨胀喷流中的流动特征，参考文献[27]～文献[31]建立了压缩波/涡混合层、压缩波/湍流混合层等模型问题，研究发现涡混合层或湍流混合层使得压缩波出现非定常运动，诱发压缩波泄漏产生具有类各向同性传播特征的声波。据此，T.Suzuki 和S.K.Lele[32]建立了激波泄漏理论。Shi Fangcheng 等[33]将该理论应用于激波/湍流混合层的声场分析中，提出了产生宽频激波噪声的两种机理。J.Berland等[34]在平面射流的模拟中观测到了激波泄漏现象，但目前尚无对轴对称非理想膨胀喷流中激波泄漏产生噪声过程的研究。

此外，数值模拟技术的发展也推动了超声速非理想膨胀喷流流场与声场的高精度模拟。I.M.A.Al-Qadi和J.N.Scott[35]于2001年实现二维欠膨胀喷流噪声模拟，由近场声场定性识别出不同类型的噪声分量。M.L.Shur 等[36-37]采用RANS-LES与FW-H方程相结合的算法模拟了三维欠膨胀喷流噪声，并讨论了锯齿喷嘴等降噪措施的机制。S.C.Lo 等[38]对比了隐式大涡模拟方法中不同过滤函数对喷流流场与声场结果的影响。冯峰等[39]基于欠膨胀喷流的模拟数据分析了马赫波与宽频激波噪声的辐射特性。此外，参考文献[9]对比了欠膨胀喷流和理想膨胀喷流的模拟数据，初步分析了不同喷流状态的流场特征差异。以上研究工作建立了针对欠膨胀喷流流场与声场的高精度模拟策略，但未详细分析欠膨胀喷流中激波波系对流场和声场的影响。

本文采用LES/FW-H混合算法模拟超声速轴对称欠膨胀喷流的流场与声场，并结合理想膨胀喷流工况的模拟结果开展对比研究。一方面探究欠膨胀喷流中激波波系对喷流流动与噪声的影响规律；另一方面基于模拟数据分析欠膨胀喷流中激波泄漏产生宽频激波噪声的过程。

1 控制方程及数值方法

本文采用混合算法模拟超声速喷流的流场与声场，即采用大涡模拟方法（LES）模拟喷流流场与近场声场，并基于声源面处的声源数据使用FW-H方程计算远场声场。本节将详细介绍上述LES/FW-H混合算法涉及的控制方程与数值方法。

1.1 大涡模拟控制方程组

忽略亚格子压力扩张项、亚格子黏性扩散项等量级较小的亚格子项，基于Favré过滤的大尺度湍流输运方程组在三维笛卡儿坐标系下为[40]

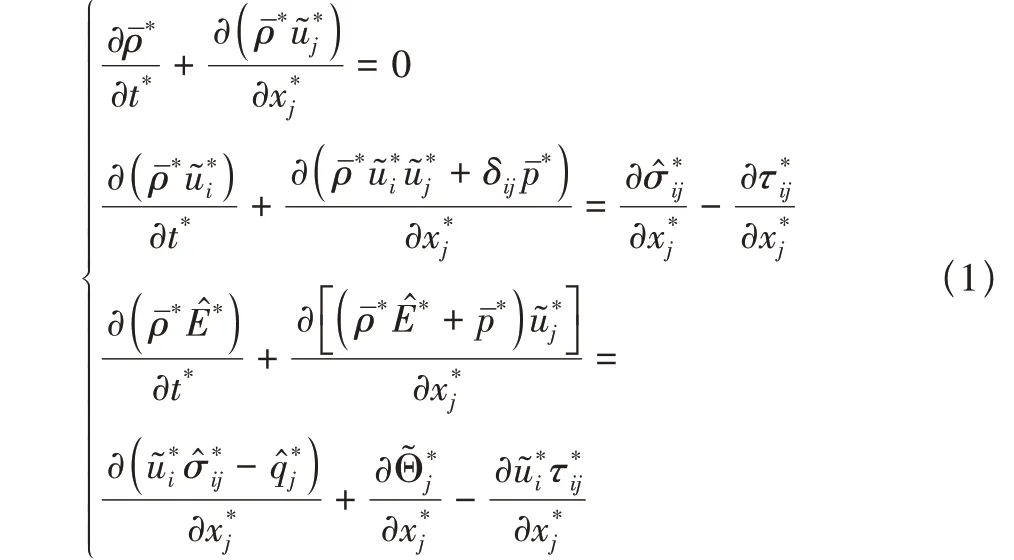
式中：“-”和“～”分别代表直接过滤与Favré过滤，“ ”代表可解尺度变量，“*”代表有量纲量。t和xj分别为时间坐标和笛卡儿空间坐标；ρ，p和uj分别为密度、压力和xj方向的速度分量；E，σij和qj分别为单位体积总能量、黏性应力和热通量；τij和Θj分别为亚格子应力和亚格子热通量。本项研究使用无黏项离散所产生的数值应力与数值耗散模拟亚格子应力和亚格子能量耗散机制，此类隐式亚格子模型已在喷流流动和喷流噪声的模拟中得到广泛应用[37,41-42]。

Favré过滤的状态方程为

式（2）确定了密度、压力和温度之间的关系。为了便于书写，本文后续将省略过滤运算相关的算符“-”“～”“ ”以及表示含量纲量的上标“*”。

1.2 FW-H方程

直接求解方程组模拟远场声传播过程需大量计算资源，而基于声类比方法求解积分方程可快速给出远场声场特征。本文采用基于可穿透声源面的FW-H方程[43-44]计算超声速喷流的远场噪声。忽略声源面外部的四极子声源，远场声观测点的噪声p′分解为厚度噪声和载荷噪声

考虑到选取的声源面处于静止状态，厚度噪声p′T和载荷噪声p′L的积分解简化为

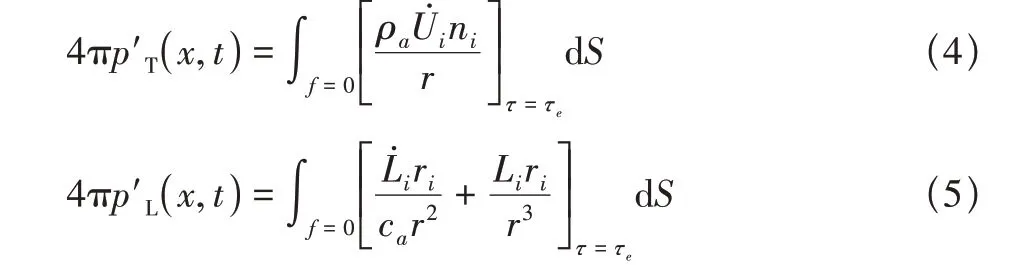
其中，f=0 为声源面坐标y构成的曲面，ρa和ca分别为环境介质的密度与声速，ri为声源指向声观测点矢量的分量，Ui，Li则分别为

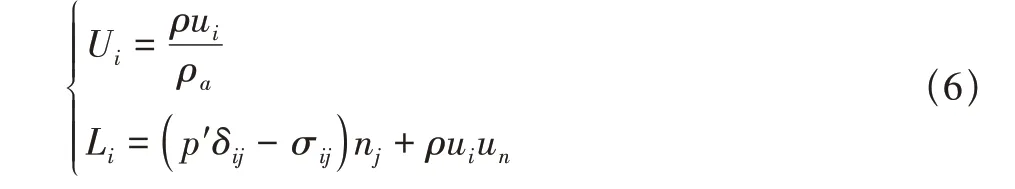
1.3 数值离散格式

采用有限差分方法对控制方程和进行离散求解，在自研软件平台[26,33]上开展数值模拟。时间推进采用具有TVD性质的三步三阶Runge-Kutta 格式[45]，黏性项离散采用4 阶中心差分格式。由于本项研究采用非均匀分布的曲面网格，无黏项离散采用满足几何守恒的7 阶WENO-FP 格式[46]，以减小网格引起的数值误差。

2 算例设计与描述

选取欠膨胀喷流（case1）作为研究对象，并设计两个理想膨胀喷流工况（case2 和case3）开展对比研究。其中，case1的喷口马赫数Maj=1.95，喷流压力比pj/pa=1.477；case2和case3 的喷口马赫数分别为Maj=1.95 和2.2，分别对应case1的喷口马赫数Maj和充分膨胀马赫数Maf。三个算例的喷嘴出口参数见表1。

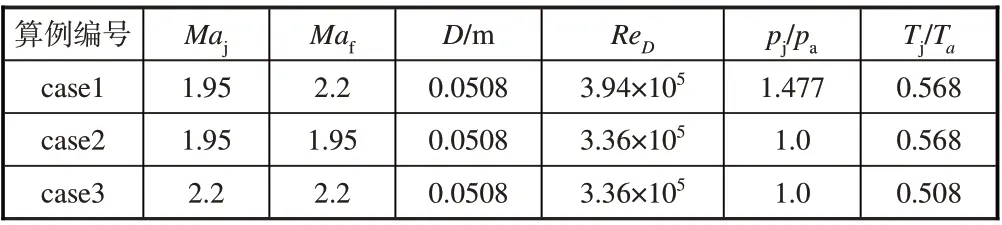
表1 喷嘴出口参数Table 1 Parameters for nozzle exit

图1 给出了喷流模拟的几何示意图。本项研究重点关注激波相关噪声中的宽频激波噪声，故喷嘴唇口厚度设为0，避免构成反馈闭环而产生啸音。此外，本算例未直接模拟喷嘴内部流动，而是采用给定喷口速度型和温度型的方式确定喷口参数。其中，速度型采用参考文献[47]的表达式

图1 喷流模拟几何示意图Fig.1 Schematic diagram of the jet simulation

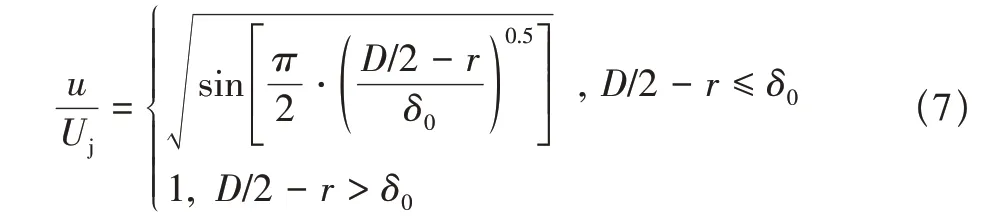
式中：δ0=0.075D。温度型采用Crocco-Busemann关系式[48]

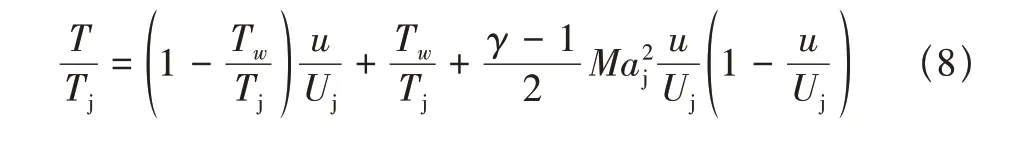
为提高数值的稳定性，将静止环境设为给定马赫数为0.01 的低亚声速流动。于是，上游与侧向边界设置为亚声速入口边界；下游边界则采用以当地马赫数为判据的超、亚声速混合出口边界。在计算域与边界之间布置缓冲区，缓冲区内无黏项离散格式采用WENO-FP 格式与AUSM+格式[49]松弛叠加，半点无黏通量Fi+1/2写成

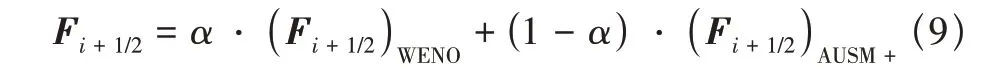
其中，α∈[0,1]为松弛系数。使用上述混合格式增大缓冲区内的数值耗散，结合网格拉伸的处理方法，可有效减小缓冲区内的湍流脉动，抑制扰动在边界处的非物理反射。

图2展示了喷流模拟计算域的网格几何拓扑结构。为避免出现极性轴问题，喷流轴线附近构建了单独的结构网格块，如图2(b)所示。网格在唇口线（r=D/2）附近进行局部加密（见图3），以便捕捉剪切层内的流动特征。同时，剪切层内湍流尺度沿流向逐渐增大，故唇口线处最小网格尺度相应进行调整（见表2）。网格在周向均布360个点，网格单元总数为5270万。

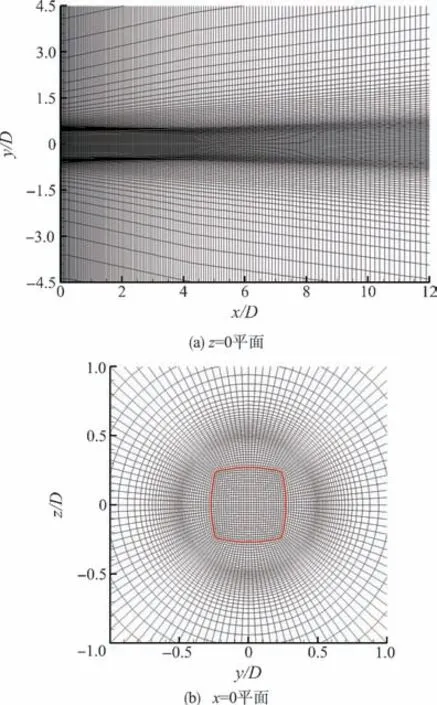
图2 计算网格(间隔三个网格点显示)Fig.2 Computational grid(every third grid is shown)

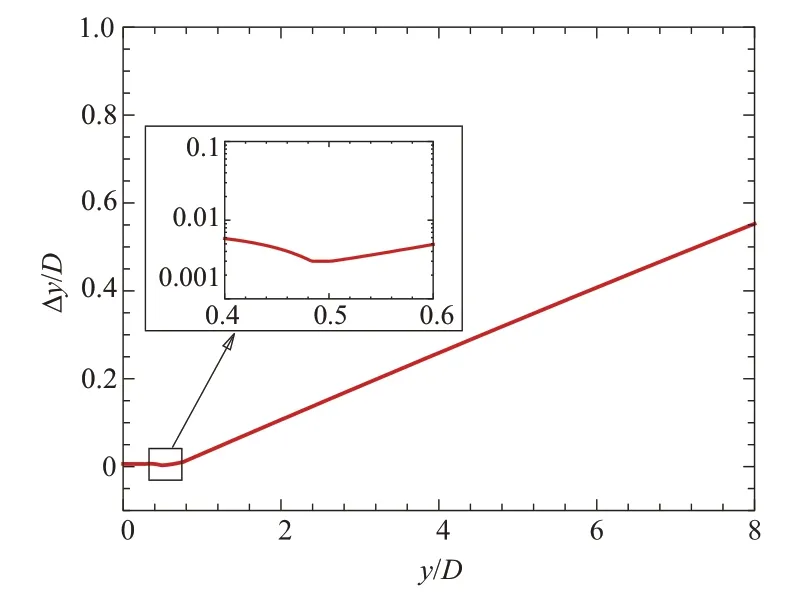
图3 直线(x,z)=(0,0)上网格间距分布Fig.3 Grid spacing distribution along(x,z)=(0,0)

表2 唇口线（r=D/2）径向网格间距Table 2 Radial spacing along the nozzle lip line（r=D/2）

合理选取声源面（FW-H方程和的积分面）是准确计算远场声场的基础，需保证声源面内部区域包含主要声源。本项研究所布置的声源面位置(xs,rs)满足以下关系式

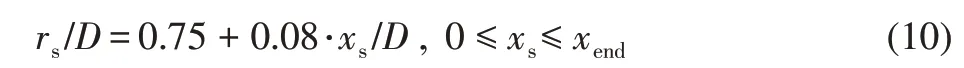
其中，xend取31.25D、32.5D、33.75D、35.0D、36.25D和37.5D。为减小伪声源，对不同xend取值的声源面辐射声场数据进行样本平均[50]。远场声观测点布置在与参考文献[38]和文献[51]相同的位置处，即以喷流出口截面中心点为圆心，半径为72D的圆弧上。

3 流场结果与分析

3.1 瞬时流场结果

图4 显示了case1 由Q判据涡识别方法给出并使用当地马赫数进行染色的喷流瞬时涡结构。喷流剪切层中扰动沿流向逐渐发展并引起流动出现失稳、转捩，进而形成充分发展湍流。在平均流的影响下，喷流下游的湍流涡沿流向方向相应拉伸。

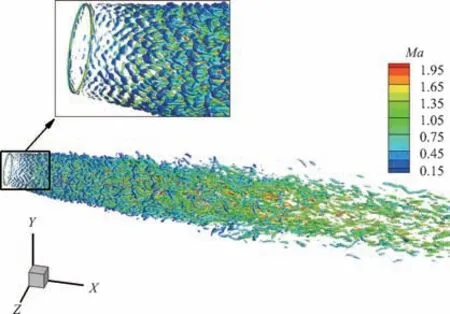
图4 case1瞬时Q判据等值面(Q=10(Uj/D)2)Fig.4 Instantaneous snapshot of eddies extracted by Q criterion(Q=10(Uj/D)2)in case1

以涡量值显示喷流剪切层内的流动结构，图5(a)给出了0≤x/D≤1.6 范围的流场瞬态云图。欠膨胀喷流自喷嘴射出后将继续膨胀，采用Prandtl-Meyer膨胀波理论[52]预测的喷流扩张角为6.74°（见图5(a)中虚线），其与数值模拟的喷流扩张角相近。喷流剪切层在x=0.64D附近开始失稳，随后逐渐演化为湍流剪切层。图5(b)采用速度散度捕捉喷流中的激波波系结构。由图5 可知，本算例中x=2.7D附近出现首次激波波系与喷流剪切层相互作用；激波波系在喷流剪切层之间反射，其强度沿流向逐渐减弱。同时，喷流剪切层厚度沿流向逐渐增大，剪切层内涡量值减小。

图5 喷流瞬态流场云图Fig.5 Instantaneous flowfield contour

3.2 流场平均特性分析

图6展示了采用平均速度散度显示激波波系结构的流场平均马赫数云图。由于欠膨胀喷流沿流向存在“膨胀—压缩—膨胀”的往复过程，剪切层中声速线与喷流轴线的间距呈现“增大—减小—增大”的变化。喷流流向不同站位处的平均马赫数径向分布如图7 所示。膨胀效应增大了x=0.25D截面处剪切层附近（0.35r/D＜0.55D）的速度，而喷流轴线附近的流动尚未受到膨胀波影响。随着喷流沿流向的发展，x=3.25D处剪切层厚度增厚。本算例模拟的平均马赫数径向分布与参考文献[53]和文献[54]中的试验数据以及数值模拟结果相符，且x=3.25D处的平均马赫数分布较参考文献[54]更接近试验数据[53]。

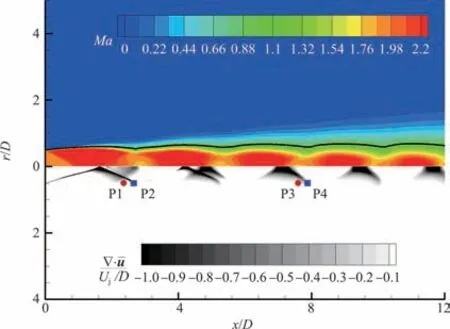
图6 流场平均马赫数与平均速度散度云图Fig.6 Mean Mach number and mean velocity divergence contour

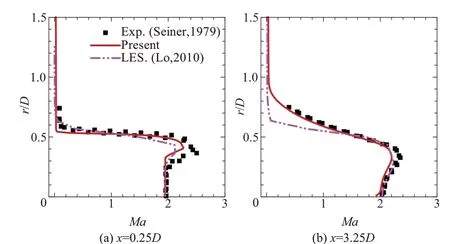
图7 流向不同站位处平均马赫数的径向分布Fig.7 Radial variation of mean Mach number at different streamwise locations

欠膨胀喷流中的激波波系结构改变了喷流轴线上的压强分布，图8(a)对比了喷流轴线上0≤x/D≤5范围内的平均压强分布。由图8 可知，本算例的数值模拟结果相比参考文献[9]、文献[39]和文献[54]更接近于试验数据[51]和理论预测值[55]。图8(b)对比了喷流轴线上0≤x/D≤20范围内的平均压强分布。由于本算例以及参考文献[9]、文献[38]、文献[39]、和[54]中数值模拟工况的雷诺数ReD均小于试验雷诺数，喷流下游（x/D≥7）的剪切层厚度增长更快，导致激波单元长度较试验结果偏短。对比本算例的模拟结果与S.C.Lo 等[38]采用LES的模拟结果，发现两者基本一致。由此可见，本算例所采用的数值方法能够准确捕捉欠膨胀喷流流场中的激波波系结构。

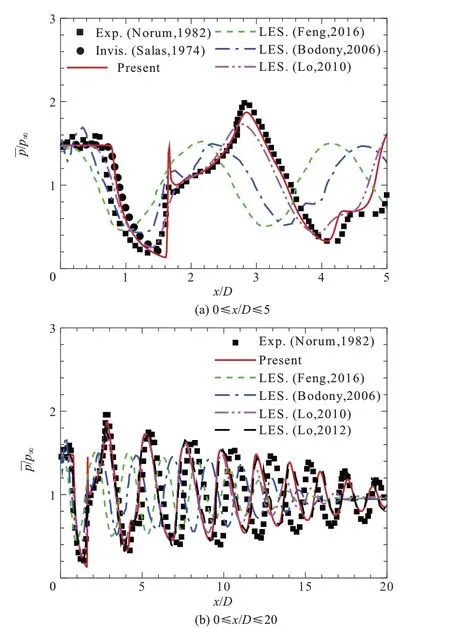
图8 喷流轴线上平均压强沿流向分布Fig.8 Centerline mean pressure in the streamwise direction

采用充分膨胀马赫数Maf对应的速度Uf无量纲（量纲一）化喷流轴线上的平均流向速度，可给出uˉ/Uf沿纵向x的分布，如图9(a)所示。图9中还对case2和case3的结果进行了对比。在两理想膨胀喷流工况中Uf=Uj。对比case2 和case3可见，case3喷口速度增大增强了可压缩效应，进而增长了喷流核心区长度、减小了喷流核心区下游流向平均速度的衰减速率。相比case2 和case3，欠膨胀喷流的核心区长度更长。将x-uˉ变换至x-1/uˉ可以发现，理想膨胀喷流和欠膨胀喷流核心区下游uˉ与x均满足反比关系

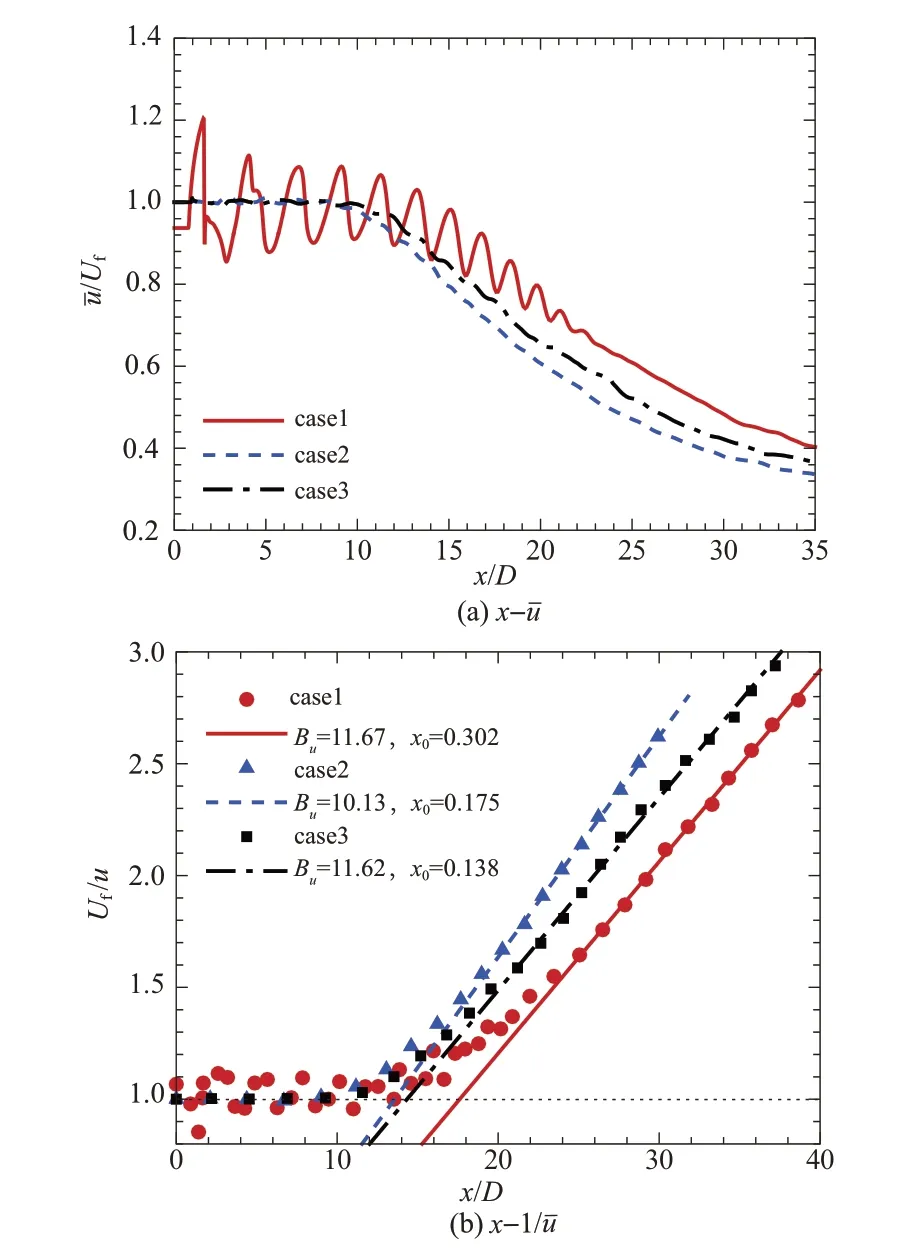
图9 喷流轴线上平均流向速度沿x分布曲线Fig.9 Centerline mean streamwise velocity in x direction

case1～case3 拟合所得的系数Bu分别为11.67、10.13 和11.62，表明case1 核心区下游平均流向速度衰减速率比case2缓慢，但与case3的衰减速率相近。定义拟合线与Uf/uˉ=1 的交点为核心区结束位置，则三个工况的核心区长度分别为xc=17.6D、13.6D和14.3D。

3.3 湍流统计特征分析

湍流脉动量是喷流流场的重要特征。图10 对比了喷流轴线上的速度脉动均方根值分布，图10 中x坐标采用核心区长度xc进行平移。欠膨胀喷流中存在的激波波系导致速度脉动值在激波波系与喷流轴线相交位置显著增大。其原因是激波波系的非定常运动使该位置处速度值呈现强烈的非定常特征。此外，三个不同工况的无量纲速度脉动u′rms/Uf和(u′r)rms/Uf在喷流核心区下游具有相近的值，反映了欠膨胀喷流中的激波波系/喷流剪切层干扰对于喷流核心区下游无量纲速度脉动强度的影响较小。值得注意的是，case1和case3的速度脉动统计量在变换到有量纲量时将显著大于case2的结果，因此欠膨胀喷流核心区下游含量纲的速度脉动值增大主要是由喷流射出喷口后继续膨胀导致平均速度增大所引起的。

图10 喷流轴线上速度脉动均方根沿x分布曲线Fig.10 Centerline root-mean-square of velocity fluctuation in x direction

在欠膨胀喷流的第一个、第三个激波波系与喷流剪切层发生相互作用的位置分别布置P1 和P2、P3 和P4 两对监视点（见图6）以研究激波波系/喷流剪切层干扰对于湍流压强脉动的影响。其中P2 和P4 处于激波作用点处，P1 和P3处于激波作用点上游，4 个监视点的空间坐标(x,r)分别为(2.53D, 0.50D)、(2.66D, 0.50D)、(7.64D, 0.50D)、(7.80D,0.50D)。图11 分别给出了P1 和P2、P3 和P4 位置处的压强脉动频谱结果。由图11可知，喷流中激波波系/喷流剪切层干扰对于中间频率段的压强脉动影响较小，但对激波作用点附近的高频和低频范围的压强脉动有增强作用。参考文献[33]基于激波/湍流混合层的研究发现，激波/湍流混合层相互作用会增强高频湍流压力脉动，但并未发现低频范围的压力脉动变化。分析欠膨胀喷流中激波波系作用引起低频压力脉动出现差异的原因在于：欠膨胀喷流中激波波系整体存在较强的低频运动，而激波/湍流混合层模型问题中只有激波波尖存在非定常运动。

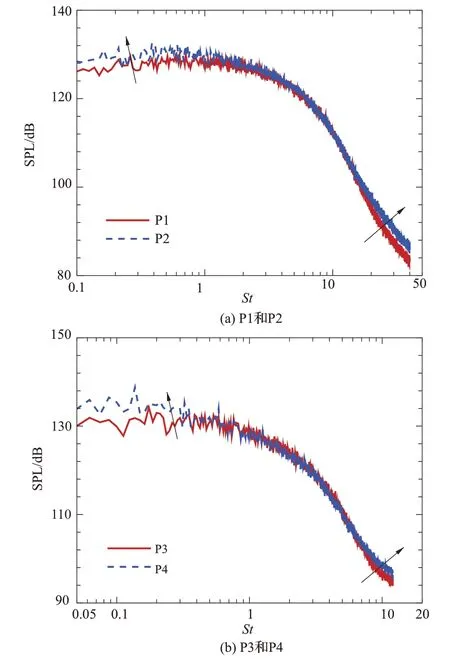
图11 监视点处压力脉动频谱对比Fig.11 Comparisons between pressure spectra at the monitors

4 声场结果与分析

4.1 近、远场声场模拟结果

本项研究采用LES模拟喷流流场与近场声场，图12分别展示了case1和case2的近场压力脉动瞬态云图。在超声速欠膨胀喷流和理想膨胀喷流中均存在以马赫波形式向喷流下游方向传播的大尺度湍流噪声，但欠膨胀喷流中的宽频激波噪声导致其侧向与上游方向压力脉动幅值明显大于理想膨胀喷流。统计近场声场数据并计算总声压级，图13定量对比了三个工况的近场声场，相同位置处case1的近场总声压级值大于case2和case3。此外，以OASPL=153dB的等值线为例，case1和case2的近场声强差大于case1和case3之间的差值，说明欠膨胀喷流射出喷口后继续膨胀所引起的速度效应增强了近场噪声。

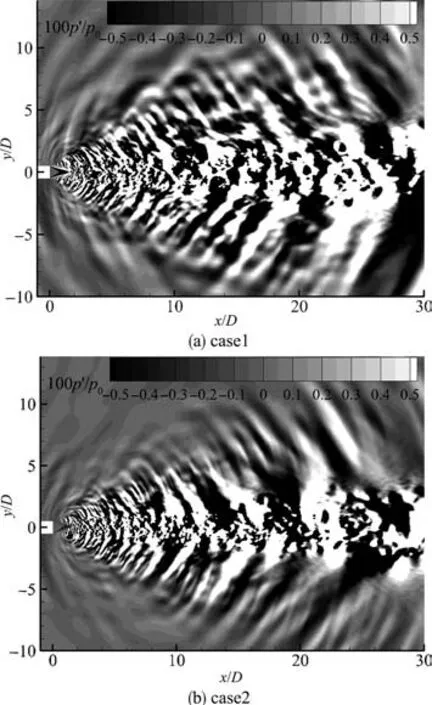
图12 压强脉动瞬态云图Fig.12 Instantaneous pressure fluctuation contours

图13 近场总声压级分布对比(单位：dB)Fig.13 Comparisons between overall sound pressure level in the near-field

基于近场声源数据求解FW-H 方程得到远场声场，图14(a)展示了case1的远场总声压级分布，并与前人的试验和数值模拟进行对比。喷流下游方向的模拟结果与T. D.Norum和J.M.Seiner[51]试验数据的最大偏差约为3dB，与S.C.Lo 等[38,54]的数值模拟结果相近；喷流侧向与上游方向声场的模拟结果与文献结果偏差小于1dB；远场总声压级峰值对应观测角θm与Lo等的峰值观测角一致，但略小于试验测量值。

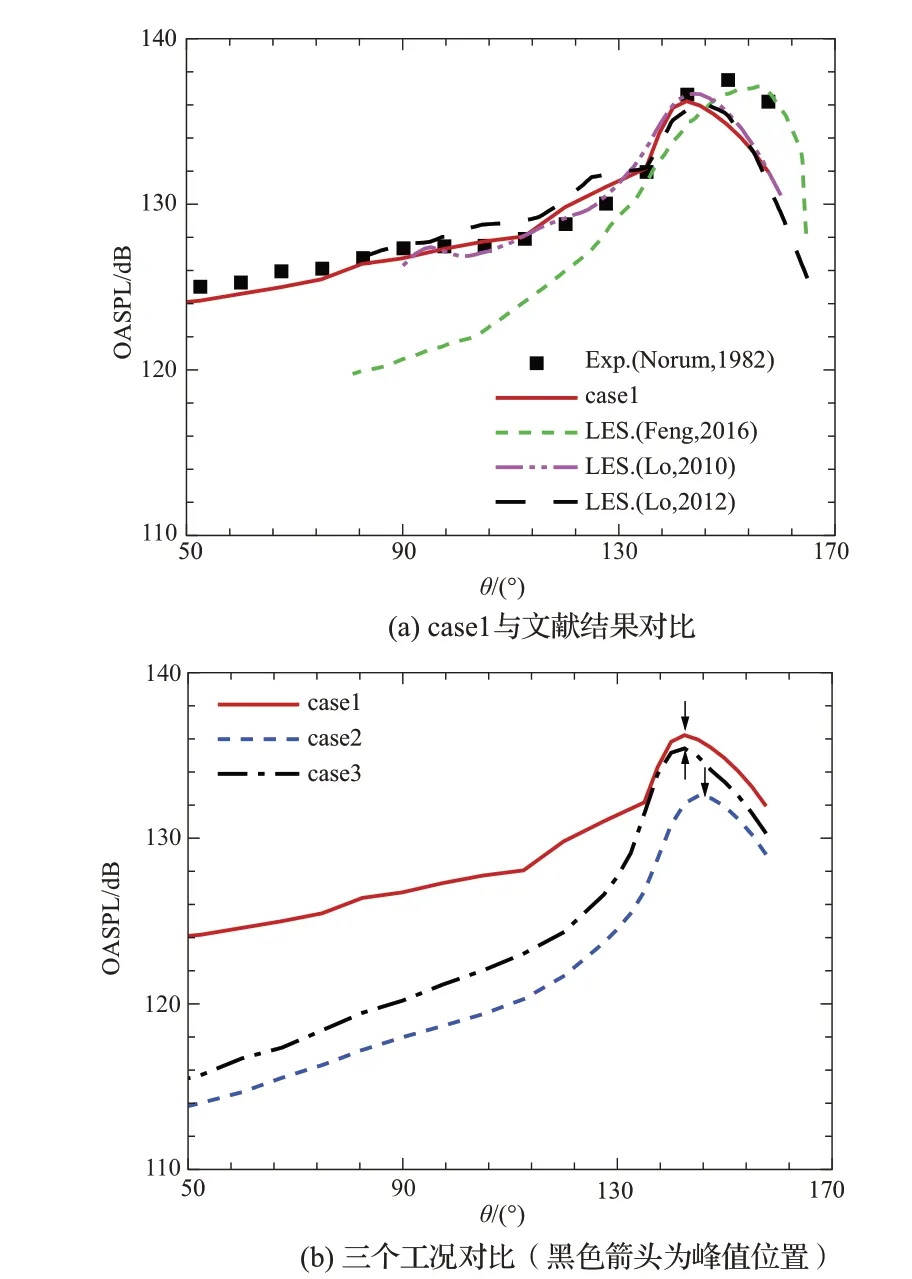
图14 远场总声压级随观测角θ变化Fig.14 OASPL vs observer angle,θ

图14(b)对比了欠膨胀喷流与理想膨胀喷流的远场总声压级值。case1 的远场总声压级峰值观测角θm小于case2，但与case3相同。因此，欠膨胀喷流中θm值主要是由充分膨胀马赫数决定的，激波波系与喷流剪切层相互作用对θm值的影响较小。此外，对比θ＜90°范围内case1～case3的总声压级值可以发现：小尺度湍流噪声主导了理想膨胀喷流的侧向与上游方向声场，故case2 与case3 的总声压级差随观测角变化较小；而欠膨胀喷流产生的宽频激波噪声显著增大了喷流侧向与上游方向的总声压级，case1 和case3的总声压级差值随观测角减小而增大。

4.2 远场声场频谱分析

在4.1节的基础上，本节基于噪声频谱统计数据分析欠膨胀喷流不同频率噪声的特征。首先，通过对比已有文献数据[38,51,56]验证模拟结果的可靠性。图15和图16分别对比了case1、case2 在θ=150°和90°两个观测角处的1/3 倍频程声压级频谱，其中频率采用喷流出口速度Uj和喷流出口直径D无量纲化。case1的模拟结果在0.03≤St≤2范围内与已有试验以及数值模拟相符，准确捕捉到了欠膨胀喷流远场噪声的峰值强度及峰值频率。case2 的喷流下游方向声场模拟结果与T. D. Norum 和J. M. Seiner[51]的试验数据吻合良好；侧向噪声的模拟结果与T.D.Norum和J.M.Seiner[51]的试验数据存在偏差，但与H. K.Tanna[56]的试验结果一致。

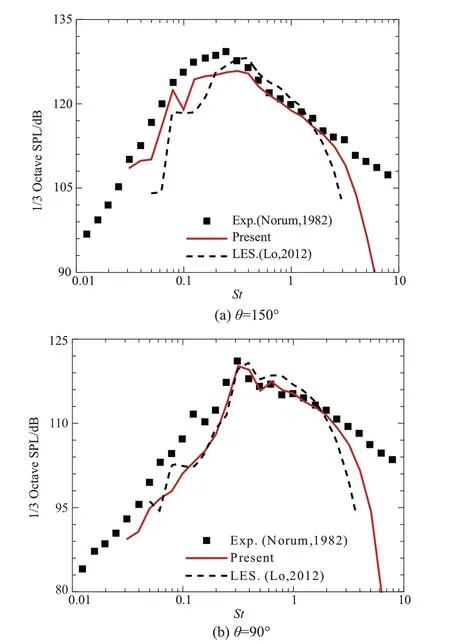
图15 case1远场1/3倍频程声压级频谱Fig.15 Far-field 1/3 octave SPL spectra in case1

图16 case2远场1/3倍频程声压级频谱Fig.16 Far-field 1/3 octave SPL spectra in case2

进一步地，图17 对比了三个工况的声压级频谱，以研究欠膨胀状态对于不同频率噪声的影响。总声压级峰值观测角处（θ=142.5°）的声场由大尺度湍流噪声占据主导，case1声压级值较case2在全频率范围均明显增大，而case1与case3的声压级频谱只在低频范围（St＜0.2）存在差别。在观测角θ=112.5°处，case1的声压级频谱受宽频激波噪声的影响，在St≈0.54附近出现一个“瘦高”的谱峰。宽频激波噪声使case1 的声压级值在St>0.2 范围内大于case2 和case3的结果，而三个工况的低频范围（St＜0.2）声压级差异较小。随着观测角的进一步减小，宽频激波噪声对应的峰值频率随之减小，case1的声压级频谱相比case2、case3在更宽的频谱范围内出现增大。

图17 远场声压级频谱曲线(相邻声压级频谱人工附加20dB以避免重叠)Fig.17 Far-field sound pressure level spectra(spectra are staggered by adding a aumulative shift of 20dB)

4.3 激波泄漏过程分析

Berland 等[34]在平面射流的数值模拟中观察到了激波泄漏现象，以下基于case1 的数值模拟结果，探讨超声速轴对称欠膨胀喷流中激波泄漏产生噪声的过程。

对于超声速欠膨胀喷流，向喷流下游方向辐射的大尺度湍流噪声导致根据z=0平面的压强脉动场无法直接识别出向上游方向传播的宽频激波噪声，如图12(a)所示。因此，需对近场压强脉动按照传播方向进行分解：首先，选取z=0 平面上0≤x/D≤16、1.2≤y/D≤9.0 范围的声场作为研究对象，提取不同时刻的压强脉动组成三维数据p′(x,y,t)；其次，采用时空Fourier 变换将空间-时间域(x，y，t)的压强脉动数据变换至波数-频率域(kx，ky，f)，并将(kx>0，f＜0)或(kx＜0，f>0)的(kx，f)数据过滤删除；最后，将过滤后的压强脉动进行Fourier，变换得到沿物理空间负x方向传播的压强脉动场p-′(x，y，t)。

利用上述压力脉动p-′结合激波波系的模拟结果，图18给出了激波泄漏过程中典型时刻的流场与近场声场云图。需要说明的是，图18 中黑色实线为声速线，红色虚线标识激波泄漏产生的声波。在激波波系从下游向上游运动的过程中，激波波系非定常运动产生了压缩波，如图18(a)和图18(b)中红色箭头标识；压缩波生成后将向低速的环境介质传播，如图18(c)所示；在图18(d)所示的时刻，前述由激波波系非定常运动产生的压缩波和基于压力脉动数据过滤得到的声波重合，验证了此声波确实由激波泄漏所产生；该声波向喷流侧向和上游方向传播，如图18(e)、图18(f)所示，形成宽频激波噪声。进一步地，提取典型空间位置(x/D,y/D)=(2,5)处沿负x和正x方向传播的压强脉动数据p-′(x,y,t)与p+′(x,y,t)，计算并对比声压级频谱，如图19所示。激波泄漏产生沿侧向和上游方向传播的噪声具有明显的声压级频谱峰值，其峰值频率与观测角θ=45°处远场声压级峰值频率（见图17）相近；而p+′声压级频谱未见明显峰值。因此，欠膨胀喷流中宽频激波噪声的高频增强效果应是源于激波泄漏产生的声波。

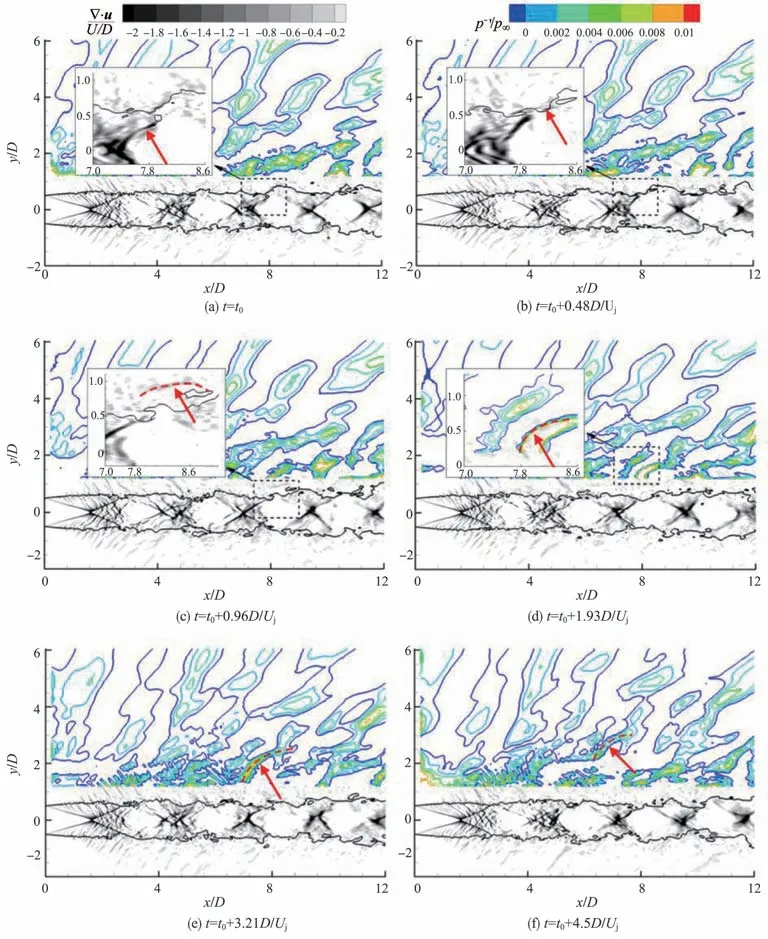
图18 z=0平面,瞬态压强脉动p-′以及激波非定常运动的可视化云图Fig.18 Visualizations of the pressure fluctuation,p-′,and the shock unsteady movement in z=0

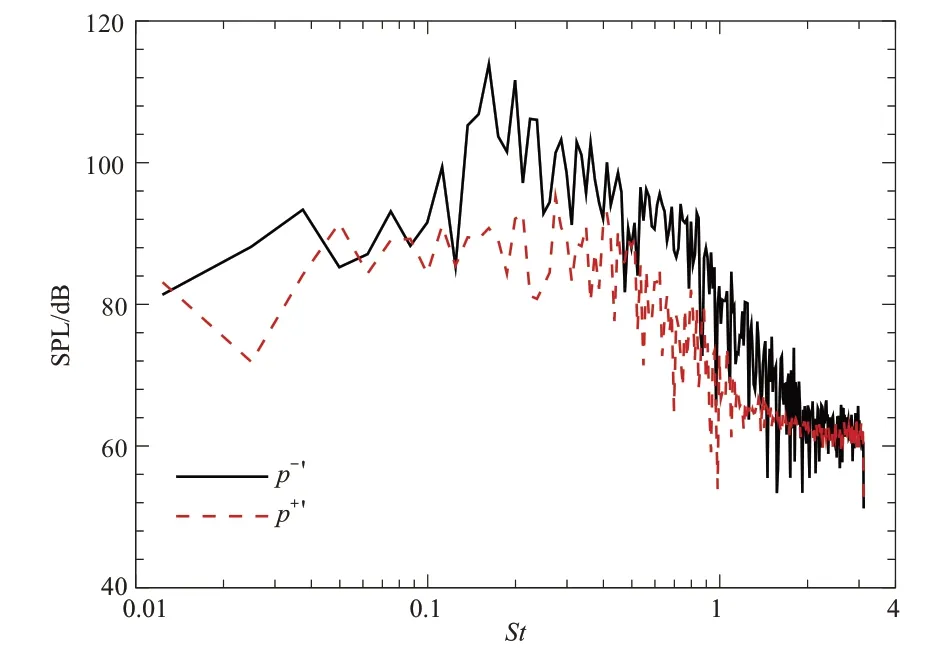
图19 p-′和p+′声压级频谱对比Fig.19 Comparison of sound pressure level spectra between p-′and p+′

数值模拟结果表明，在激波波系从上游向下游运动过程中不会引发激波泄漏而产生声波，其与参考文献[33]对激波/湍流混合层相互作用模型问题的研究结论一致。

5 结论

本文采用LES/FW-H混合算法模拟了超声速欠膨胀喷流噪声，并设计理想膨胀喷流工况开展对比研究，探究了欠膨胀状态下喷流的流场与声场特征，明确了欠膨胀喷流中由激波泄漏产生宽频激波噪声的过程。研究发现：

（1）欠膨胀喷流射出喷口后继续膨胀将增大喷流速度，增强可压缩效应，其减缓了欠膨胀喷流核心区下游平均速度衰减速率，同时增大了核心区下游湍流速度脉动值。

（2）超声速欠膨胀喷流中激波波系/喷流剪切层干扰会增强激波作用点附近的高频和低频压强脉动值，但不改变中间频率段的压强脉动。

（3）欠膨胀喷流远场总声压级峰值及其对应观测角值与充分膨胀马赫数对应的理想膨胀喷流相近。欠膨胀喷流中的宽频激波噪声显著增强了侧向与上游方向声场，其增强效果集中在高频范围。

（4）欠膨胀喷流中激波波系与喷流剪切层相互作用导致激波由下游向上游运动时出现激波泄漏现象，其产生了向喷流上游方向传播的宽频激波噪声。而激波由上游向下游运动过程中不会产生此类声波。