汽轮机低压缸末级长叶片水蚀研究

杨建道

(上海汽轮机厂有限公司， 上海 200240)

在“双碳”的目标指引下，我国将大力推进能源结构的调整和转型升级，能源生产结构由煤炭为主向多元化转变，能源消费结构日趋低碳化，非化石能源占能源消费的比重将越来越高。常规火电机组参与深度调峰，这将导致火电机组汽轮机低压缸一直存在的湿蒸汽流动问题更加凸显[1]。汽轮机级效率会在湿蒸汽工作区显著降低，进而导致叶片做功能力下降；同时，湿蒸汽中的水滴会导致汽轮机低压缸末几级长叶片发生严重的水蚀损坏，影响长叶片的使用寿命。

根据形成机理的不同，可将湿蒸汽级内的水滴分为一次水滴和二次水滴。蒸汽在汽缸流道内膨胀到Wilson线时发生自发凝结，产生大量直径为0.01～1.0 μm的微小水滴，这些水滴被称为一次水滴；大部分一次水滴跟随蒸汽流动，而小部分一次水滴由于惯性和扩散作用沉积到静叶表面形成水膜，在汽流切应力作用下向静叶尾缘移动并逐渐凝聚长大，最后在静叶出汽边撕裂形成直径较大的二次水滴[2]。2种水滴的动力学特性有着显著的不同，具体为：一次水滴与汽流有良好的跟随性，二次水滴则与汽流有较大的速度滑移。二次水滴在运动中偏离汽流方向撞击动叶吸力面，从而产生制动损失。

二次水滴撞击末级动叶时除了会带来制动损失，还会对动叶产生水蚀。当大量直径较大的二次水滴冲击动叶表面时，水滴由球状变成了膜状，并且在动叶接触部分内部产生很大的压力，在这种压力的反复作用下，叶片一旦达到材料的疲劳极限，便开始产生疲劳裂纹。水滴冲击到这种裂纹内部时，水滴内部的压力将使裂纹向更深处发展，致使叶片材料从动叶表面脱落而形成水蚀，严重时还会导致叶片断裂，造成事故[3]。

以某汽轮机低压缸末三级叶片为研究对象，通过数值计算的方法获得了其在不同工况下的流场，并且结合粒子输运模型，探究低压缸末级动叶在不同出口湿度下二次水滴的制动损失和制动力的变化，同时给出各叶高段所受到的气动压力和水锤压力，为其水蚀分析提供参考。

1 计算模型和数值方法

1.1 计算模型及网格划分

图1为汽轮机低压缸末三级叶片带抽汽口的计算模型。为了减少边界对内部流动的影响，对低压缸进出口和抽汽口出口均进行适当延伸。

图1 低压缸末三级叶片的计算模型

采用NUMECA软件中的AutoGrid5模块生成各级动、静叶通道和抽汽口结构的计算网格，所采用的网格为多块结构化网格。各级叶片、轮毂和汽缸壁外第一层网格的间距取0.01～0.02 mm，以保证绝大部分区域y+在0～10。网格的总节点数约为380万。图2为各级叶栅50%叶高截面和抽汽口的网格。

图2 各级叶栅50%叶高截面及抽汽口的网格

1.2 数值方法

采用商业计算流体动力学(CFD)软件中ANSYS CFX软件进行数值求解，使用平衡态凝结和非平衡态凝结2种模型来模拟蒸汽在汽轮机低压缸内的流动。湿蒸汽是蒸汽和大量水滴的混合物，已有比较成熟的模型来描述由自发凝结形成的水滴(一次水滴)。对于由沉积在壁面(叶片、汽缸壁)的水膜被汽流撕裂雾化形成的二次水滴，由于其形成过程极其复杂，还没有完善的模型来模拟该过程，并且二次水滴的运动对流场的影响很小，因此在本文中对此不予考虑。

将水和蒸汽作为工质进行计算时，为使Navier-Stokes控制方程封闭，必须对水和蒸汽的状态参数给出定量的关系，因此对其性质进行精确计算时，不能将其简单地当作理想气体来处理，采用ANSYS CFX软件内置的基于IAPWS-IF 97公式的真实蒸汽性质模型。

使用非平衡态凝结模型对透平级中的凝结流动进行模拟，只能获得湿蒸汽流动中一次水滴的分布情况。为了研究湿蒸汽中二次水滴的运动，还需要采用粒子输运模型。粒子运输模型是一种欧拉-拉格朗日多相流模型，流场在欧拉坐标系中进行求解，而粒子运动轨迹用拉格朗日法追踪。采用单一粒子样本形成一组微分方程，同时采用包括位置、速度、温度和质量组分的方程来追踪粒子。

在粒子输运模型中，通过追踪流场中的一部分粒子(样本)来模拟整体粒子的流动。粒子位移通过在时间步长内粒子速度的向前欧拉积分法获得。粒子位移为：

xi,new=xi,old+vp,i,oldδt

(1)

式中：xi,new、xi,old分别为粒子i位移的新值和旧值；vp,i,old为粒子i的速度；δt为时间步长。

在向前欧拉积分中，假设在时间步长开始计算的粒子速度用于整个时间步长。在时间步长的末尾，新的粒子速度可以由粒子动量方程的解析解获得。具体方程为：

(2)

式中：mp为粒子质量；vp为粒子速度；t为时间；Fall为作用在粒子上力的总和。

粒子动量方程的解析解可以表示为：

vp=vf+(vp0-vf)exp(-δt/τ)+

τFall[1-exp(-δt/τ)]

(3)

式中：vf为流体速度；vp0为初始时刻粒子速度；τ为粒子在流体中的运动时间。

流体属性在时间积分的初始时刻获得。计算湍流中的粒子运动轨迹时，特别是对于直径较小的粒子(如一次水滴和直径很小的二次水滴)，还要考虑湍流扩散效应。湍流扩散是指粒子在湍流脉动作用下，由粒子体积分数较高的区域向粒子体积分数较低的区域扩散的现象。湍流的瞬时速度可分解为时均速度和脉动速度，由于脉动速度具有随机性，受到湍流作用的粒子轨迹也表现出随机性，因此考虑湍流扩散效应时需要计算大量的粒子数。

在ANSYS CFX软件中使用Gosman和Ioannides发展的湍流扩散模型。该模型假定一个粒子总是位于一个湍流旋涡内，每个湍流涡具有脉动速度、生存期和尺度3个特征参数，具体的表达式为：

(4)

(5)

τe=le/(2k/3)1/2

(6)

当粒子位于某个湍流旋涡内时，即粒子在这3个特征参数的作用下运动，直到该旋涡消失或粒子进入下一个旋涡时，粒子才会受到新的特征参数的作用。

1.3 研究方法

为了便于研究二次水滴撞击末级动叶的实际情况，将末级(第6级)静叶和动叶沿叶高划分为11等份(见图3)，并且将静叶和动叶从叶根到叶顶的各段分别命名为S1～S11、R1～R11。然后，在末级静叶出汽边附近沿叶高设置11个等距的二次水滴进入点，考虑静叶尾缘出口“水舌效应”，将二次水滴样本放置于每个叶高段中间叶高静叶尾缘下游3 mm的位置(见图4)。

图3 末级动叶和静叶沿叶高等分示意图

图4 水滴粒子的释放位置

沿叶高释放的二次水滴粒子进入流场后，可以通过ANSYS CFX软件中的粒子输运模型对其进行计算，获得二次水滴粒子在低压缸末级叶片中的流动轨迹，以及二次水滴撞击末级动叶表面的位置和速度。

图5为二次水滴最大直径沿叶高的分布。每个叶高段释放的水滴直径取由临界韦伯数确定的二次水滴最大直径。末级静叶出口二次水滴质量流量为91.950 4 kg/s，出口平均相对湿度为9.271%，对应的液态水滴质量流量为8.524 6 kg/s。由文献[4-7]中的方法确定末级静叶出口二次水滴在水分中的质量占比约为17.87%。因此，末级静叶出口边产生的二次水滴的质量流量约为1.523 3 kg/s，并且确定了沿各叶高段中二次水滴的质量流量分布(见图6)。

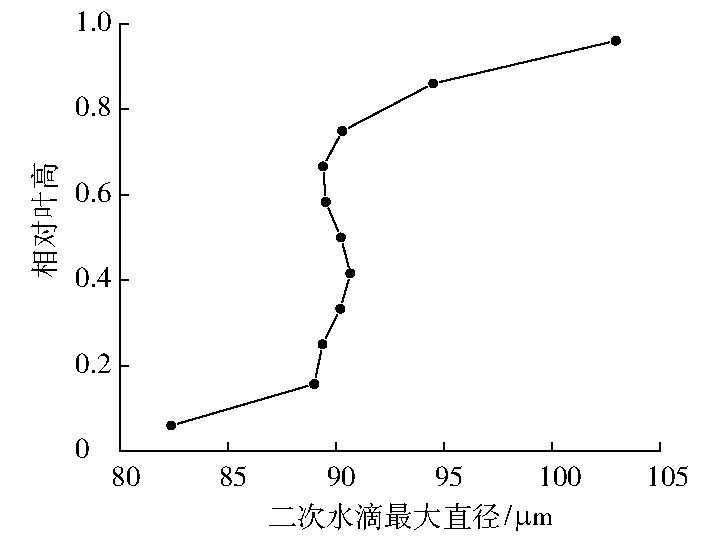
图5 二次水滴最大直径沿叶高的分布

图6 二次水滴质量流量沿叶高的分布

2 结果与分析

2.1 二次水滴的运动轨迹

图7为不同直径的二次水滴在末级静叶和动叶通道内的运动轨迹。由于给出的是相对坐标系下的轨迹，因此动静交界面上的轨迹并不连续。

图7 二次水滴在末级静叶和动叶通道内的运动轨迹

由图7可得：二次水滴的运动轨迹受到汽流力、湍流和惯性的共同作用；二次水滴的直径越大，惯性也越大，同时受到汽流力和湍流的影响相对越小，其运动轨迹偏离汽流方向也越明显。20 μm二次水滴整体上仍能够跟随汽流运动，其运动轨迹与汽流方向的偏离较小，大部分都通过了动叶通道，只有少数沉积在动叶吸力面前部、压力面中后部和汽缸上端壁；70 μm二次水滴的运动轨迹已经与汽流方向发生明显的偏离，一部分流出了动叶通道，另一部分沉积在动叶吸力面前部、压力面后部和汽缸上端壁；100 μm二次水滴受到汽流力的作用已经相对较小，大部分沉积在动叶吸力面前部和汽缸上端壁；120 μm二次水滴则几乎依靠惯性运动，全部沉积在静叶吸力面前部。

图8为二次水滴的撞击区域。

图8 二次水滴的撞击区域

该低压缸末级静叶出口二次水滴平均最大直径约为90.77 μm，并且二次水滴直径沿叶高方向逐渐增大，在动叶顶部附近二次水滴直径达到102.96 μm，可见二次水滴对末级动叶前缘的撞击效应显著，特别是叶顶附近。同时，由粒子输运模型计算可以确定二次水滴撞击动叶前缘的集中区域(见图8(a))。

另外，末级动叶属于长叶片，沿叶高方向受离心力的作用，汽流携带二次水滴向叶顶方向汇聚；大量二次水滴撞击到了汽缸上端壁和动叶顶部，并且部分二次水滴撞击汽缸上端壁后反弹，再一次和动叶顶部发生撞击(见图8(b))。进一步分析发现，二次水滴撞击汽缸上端壁主要集中在两个区域，一个是动叶叶顶正上方汽缸壁，另一个区域位于动叶叶顶尾缘下游约46 mm后，沿轴向的作用宽度达到了约62 mm，撞击效应十分显著(见图8(c))。

2.2 二次水滴的制动损失和制动力

图9为二次水滴对末级动叶的作用力。通过粒子输运模型进行计算，可以获得11个直径的二次水滴样本撞击末级动叶表面的制动位置和制动速度，同时结合对应的动叶截面叶型确定二次水滴的制动长度。分别计算动叶R1～R11各叶高段上的制动损失和制动力。

图9 二次水滴对末级动叶的作用力

二次水滴对动叶表面的撞击效果可用水锤压力来衡量。水锤压力的表达式为：

(7)

式中：p为水锤压力；ρd、vd分别为二次水滴的密度、声速；wd为二次水滴撞击动叶前缘的制动速度；ρM、vM分别为动叶钢材料的密度和声速，ρM取7 850 kg/m3，vM取5 920 m/s。

每个叶高段受到的轴向制动力和周向制动力的表达式为：

Fa=N·p·φ·l·h·sinβ

(8)

Fr=N·p·φ·l·h·cosβ

(9)

式中：Fa为轴向制动力；Fr为周向制动力；N为末级动叶叶片数；h为各叶高段的叶高；φ、l、β分别为各叶高段二次水滴的体积分数、制动长度和制动角。

不同叶高段的制动损失的表达式为：

ΔP=N·ω·p·φ·l·h

(10)

式中：ΔP为制动损失；ω为末级动叶转速。

表1为末级动叶各叶高段二次水滴的制动损失，各叶高段合计的轴向制动力、周向制动力和制动损失分别为238.64 N、1 123.10 N、364.70 kW。由表1可得：末级动叶顶部(R11叶高段)是受二次水滴冲击最严重的区域，其轴向制动力、周向制动力和制动损失在整个末级动叶中的占比分别为17.73%、28.96%、28.26%。结合二次水滴在末级动叶的运动轨迹可知，在径向离心力的作用下，较多的二次水滴向动叶顶部汇聚，不断撞击动叶顶部和汽缸上端壁，部分水滴从汽缸上端壁反弹后对动叶顶部进行二次撞击，加剧了动叶顶部的水蚀。

表1 末级动叶各叶高段二次水滴的制动损失

图10为末级动叶各叶高段所受气动压力和水锤压力的示意图，其中：各叶高段所受水锤压力方向沿二次水滴相对速度方向；气动压力取湿蒸汽流场CFD软件计算结果中的叶片表面平均压力。

图10 末级动叶各叶高段受力的示意图

由图10可得：R11叶高段所受的气动压力和水锤压力均是最大的，说明在相同面积的二次水滴撞击区域上，R11叶高段所受到的汽流力和二次水滴制动力也是最大的。当末级动叶发生水蚀破坏时，其叶顶R11叶高段是最危险的区域。

2.3 不同工况下的水蚀分析

图11为50%热耗率验收(THA)工况末级静叶出口二次水滴最大直径沿叶高的分布。50%THA工况下低压缸的质量流量约为THA工况的一半。50%THA工况下，该低压缸末级静叶出口二次水滴平均最大直径约为116.83 μm，并且二次水滴直径沿叶高方向逐渐增大，在动叶顶部附近，二次水滴最大直径达到144.82 μm。图12为50%THA工况下末级静叶出口二次水滴质量流量沿叶高的分布。与THA工况相比，50%THA工况下末级动叶进口前的二次水滴直径更大。末级静叶出口二次水滴质量流量为46.794 2 kg/s、出口平均相对湿度为6.405 6%，对应的液态水滴质量流量为2.997 4 kg/s，末级静叶出口二次水滴在水分的质量占比约为17.87%。因此，末级静叶出口边二次水滴的质量流量约为0.535 6 kg/s。

图11 50%THA工况末级静叶出口二次水滴最大直径沿叶高的分布

图12 50%THA工况下末级静叶出口二次水滴质量流量沿叶高的分布

图13为50%THA工况下二次水滴在末级静叶和动叶通道内的相对运动轨迹。小容积流量下二次水滴的直径变大，惯性也越大，受到汽流力和湍流的影响较小，运动轨迹明显偏离汽流方向，大部分二次水滴以较大的负攻角撞击末级动叶吸力面前缘。

图13 50%THA工况二次水滴在末级静叶和动叶通道内的相对运动轨迹

此外，与THA工况相比，50%THA工况下二次水滴以更大的制动速度撞击在末级动叶上，产生了更大的水锤压力，导致末级动叶水蚀进一步加剧。末级动叶R11叶高段范围内轴向制动力、周向制动力和制动损失在整个末级动叶中的占比分别为20.75%、32.06%、32.06%，该部位为受二次水滴冲击最严重的区域。

从THA工况到50%THA工况，由于低压缸容积流量的减小，静叶出口汽流速度降低引起的水蚀率的增加量远大于湿度增加引起的水蚀率的减小量，最终表现为水蚀率增大。图14为大容积流量与小容积流量下水蚀机理的对比。造成这种差异的具体原因[9]为：造成动叶水蚀的水分不是全部水分，而是湿蒸汽在静叶表面沉积形成水膜后在静叶出汽边进一步撕裂形成的二次水滴；当容积流量减小后，静叶出口汽流速度降低，水滴的绝对速度也降低，而圆周速度不变，导致水滴与叶片的相对速度增大，从而导致水蚀率增大。

图14 大容积流量与小容积流量下水蚀机理的对比

3 结语

采用数值模拟的方法对THA、50%THA工况的湿蒸汽两相流场进行分析，获得末级静叶出口二次水滴直径和质量流量的分布，结合粒子输运模型获得二次水滴在末级动叶产生水蚀的位置，以及二次水滴撞击动叶产生的制动力和制动损失的分布。得到的主要结论为：

(1) 末级动叶顶部(1/11叶高范围)的轴向制动力、周向制动力和制动损失在整个末级动叶中的占比较大，50%THA工况下分别为20.75%、32.06%、32.06%。该部位为受二次水滴冲击最严重的区域。

(2) 与THA工况相比，50%THA工况下末级静叶出汽边二次水滴的直径显著增大，二次水滴以更大的制动速度撞击在末级动叶上，产生了更大的水锤压力。

综上可知，低压末级长叶片在小容积流量下将承受更严重的水蚀，所以火电机组在参与深度调峰时，如何采取防水蚀措施以延长末级长叶片寿命将十分重要。