微积分中常用经济最优化问题解决方案的分析

□焦 华

在经管类微积分教程中一定包括有微分学和积分学在经济学中的应用，这是和理工类微积分不一样的地方。反映到具体章节上通常有常用经济函数、经济学中的导数(边际与弹性)、数学建模——最优化、积分在经济分析中的应用等。这里常用经济最优化问题是指：已知需求函数或价格函数，就可以确定收入(益)函数。若还已知成本函数，就可以确定利润函数。最优化就是求利润函数的最大值点、最大值。解决问题的工具就是微积分中的导数(一阶及二阶导数)。

一、常用经济最优化问题的一元函数模型

需求函数Q=f(P)刻画的是商品的需求量与价格之间的函数关系，这是一个单调减函数，价格越高需求量越小，价格越低需求量越大，P=0(不要钱)时需求量达到最大。需求函数是一个神奇的函数，知道公司的定价，就能确定它的销量；反过来，知道公司的销量就能推算出它是以什么价格卖出去的。那这个神奇的函数是怎么得到的呢？应该是经验公式或统计数据的拟合——线性回归或非线性回归等……需求函数的反函数是价格函数，它们可以相互推出Q=f(P)⟺P=f-1(Q)，即互为反函数。

由两者之一可推出收入函数R=P·Q=P·f(P)=Q·f-1(Q)，如果已知成本函数C=g(Q)，则可推出利润函数L=R-C=Q·f-1(Q)-g(Q)=P·f(P)-g(f(P))。因此利润函数可以是销量的函数也可以是售价的函数，具体怎样选择视问题的要求而定。利润函数确定后，接下来求最大利润就是求函数的最大值，用微积分的方法，首先由极值的必要条件找到驻点(求一阶导数)，其次由极值的充分条件验证驻点是极大值点(求二阶导数)，最后通常用到“唯一的极值点必是最值点”得到问题所需的结论。下面通过三个实例来说明解决这类问题的方法和步骤。

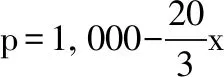
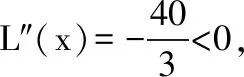
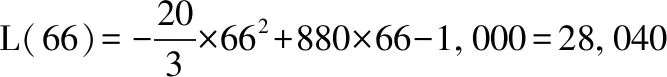
注：该题也可用初等的配方法得到解决。

实例2：某企业生产某种产品的总成本函数为C(x)=60x+2,000，该产品的需求函数为x=1,000-10p(其中x为需求量，p为价格)，求：(1)收入函数R(x)及利润函数L(x)；(2)产量x为多少时，利润达到最大？

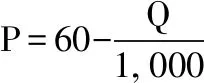
(2)当P=50时的边际利润，并解释其经济意义；

(3)使得利润最大的单价P。

(1)总收入函数R(P)=PQ=1,000P(60-P)=60,000P-1,000P2,

总成本函数C(P)=60,000+20Q=1,260,000-20,000P,

总利润函数L(P)=R(P)-C(P)=-1,000P2+80,000P-1,260,000,

注意到前面两个实例中利润函数是产量的函数，而该实例利润函数是价格的函数，这样做是为了解决第2个和第3个小问，此时边际利润L′(P)=-2,000P+80,000;

(2)当P=50时的边际利润L′(50)=-20,000，其经济意义为在P=50时，价格每提高1元，总利润减少20,000元。

因此L(P)在(0,40)递增，在(40，+∞)递减，由极值的第一充分条件驻点P=40是极大值点。由于唯一的极值点是最值点，所以当P=40时，总利润最大。

通过前面三个实例可看出：x或Q在需求函数或价格函数中代表的是需求量；在收入函数中代表的是销量；在成本函数中代表的是产量；在企业实际经营活动中，这三个量通常是不相等的。因此能够完美利用微积分解决这类问题是作了理想假设的，那就是：需求量=销量=产量。如果没有这样的假设前题，上面的解法将“土崩瓦解”。提出边际与弹性的经济学家阿尔弗雷德-马歇尔曾指出:经济学具有和物理学相类似的科学性。物理学中有理想实验、理想假设，比如匀速直线运动、忽略空气阻力等，将实际问题的模型简化有助于问题的解决，追求的是大致的正确。因此上面的理想假设“需求量=销量=产量”是允许的。再有前面三个实例都应用了“唯一的极值点是最值点”这一结论，这种简略方式并不严谨，该结论可详尽地描述为：函数f(x)在闭区间[a,b]上连续，在开区间(a,b)上可导，而且函数有唯一的极值点(有极大值就没有极小值，有极小值就没有极大值)，那么该极值点就是函数在闭区间[a,b]上的最值点。这个可以当成定理用的重要结论很多微积分或高等数学的教材没有表述清楚，甚至有本全国通用的微积分教材出现了只要求“函数f(x)在闭区间[a,b]上连续”、漏掉了“在开区间(a,b)上可导”这样的错误。

二、常用经济最优化问题的多元函数模型

上面是常用经济最优化问题的一元函数模型，下面讨论它的多元函数模型，以二元函数为例，其余以此类推。此时问题的提出通常是一个企业(公司)的两种产品市场或一种产品的两个独立市场，于是出现了两个需求函数：Q1=f(P1),Q2=g(P2)或Q1=f(P1，P2),Q2=g(P1,P2)，后一种情形表达的是两种产品具有互相关联或可互相替代的属性。当然这类问题也可以用两个价格函数代替两个需求函数。于是收入函数、成本函数、利润函数都变成了二元函数，用多元函数微分学的工具解决问题。实例如下：

实例4：某工厂生产的同一种产品分销两个独立市场，两个市场的价格函数分别为：P1=60-3Q1,P2=20-2Q2,总成本函数为C=12(Q1+Q2)+4,工厂追求最大利润，求此时投放每个市场的产量为多少？

解：由题设两个市场的总收益函数为：

从而工厂的利润函数为：

AC-B2=24>0,A<0,故由极值的充分条件(8，2)是极大值点。

由于唯一的极值点必是最值点，所以当投放每个市场的产量分别为8和2时工厂可获得最大利润。

实例5：设某公司生产甲、乙两种产品，这两种产品的产量已知分别为q1和q2时，销售价格分别为：p1=120-5q1和p2=200-20q2，总成本为C(q1,q2)=35+40(q1+q2)，问甲、乙两种产品产量为多少时，能使该公司获得的总利润达到最大？最大利润又是多少？

解：总收益为R(q1,q2)=p1q1+p2q2=120q1-5q12+200q2-20q22

总利润为：L(q1,q2)=R(q1,q2)-C(q1,q2)

=80q1-5q12+160q2-20q22-35

Lq1=80-10q1,Lq2=160-40q2

令，Lq1=80-10q1=0,Lq2=160-40q2=0得驻点q1=8,q2=4

在q1=8,q2=4处，有

Lq1q1=A=-10,Lq1q2=B=0,Lq2q2=C=-40

AC-B2>0,又A<0

由极值的充分条件(8，4)是极大值点。由于唯一的极值点必是最值点，所以在q1=8,q2=4时，该公司获得最大利润，最大利润是L(8,4)=605。

实例6：设q1为某商品A的需求量，q2为某商品B的需求量，两种商品需求函数分别为

q1=16-2p1+4p2,q2=20+4p1-10p2

总成本函数为C=3q1+2q2,p1,p2为商品的价格，试问价格p1,p2取何值时，企业可使利润达到最大？

解：总收入函数为R=p1q1+p2q2

于是，总利润函数为：L=R-C=(p1-3)q1+(p2-2)q2

=(p1-3)(16-2p1+4p2)+(p2-2)(20+4p1-10p2)

注意：与前面两个实例不同，该实例中需求函数中q1不仅与p1有关，还与p2有关；q2不仅与p2有关，还与p1有关，如何理解？具体教学过程中教师应当讲清楚A与B是关联商品、是可替代商品，比如食盐与酱油、两个不同厂家的腊香肠等，这样学生就能较好地理解该实例中的需求函数。

三、结语

在经管类微积分教程中包含的微积分在经济学中的应用，数学内容并不复杂，关键是要理解其经济学相关的概念的含义。这部分内容是微积分和微观经济学的交叉结合，多数微积分教材讲得不够通透，是因为作者专业背景是数学，对经济学缺乏深入研究，但微积分作为公共基础课，不能期待它解决所有的问题，它能给予学生一个扎实的数学基础就行，剩下的交给后续课程的专业课教师。