基于一致性度量的数字孪生模型实时自修正
徐 麟,何月顺,宋伟宁,许婷婷
(东华理工大学信息工程学院,江西 南昌 330013)
0 引 言
随着科学技术的日益发达,全球各国也相继提出了不同的先进制造技术发展转型战略,如德国的工业4.0,美国的工业互联网以及中国制造2025和互联网+制造等[1-6]。数字孪生是解决工业互联网的信息物理融合难题的关键技术,已经得到了众多国内外学者的广泛关注和研究。数字孪生通过模拟实体对象在数字世界中的活动,并通过对虚拟对象和现实之间的互动反应、数据融合分析以及决策迭代优化,增强实体的能力[7-11]。物理实体和虚拟模型是数字孪生的2种核心要素,以仿真技术为主要基础的虚拟模型的建立是数字孪生的基本保障[12]。数字孪生则充分利用模型、数据和集成多学科技术,将物理世界和数字世界连接起来,从而提供更高效、智能的服务[13]。
目前,数字孪生技术在产品设计、制造和服务中的应用研究已成为世界上许多知名企业和学者的研究课题。PTC公司将数字孪生作为“智能互联产品”的关键环节,在虚拟空间和物理空间构建一条数字纽带,基于数字孪生技术为客户提供高效的产品售后服务与支持[14]。美国国防部根据飞行器的物理结构,结合航天飞行器的运行服务数据,建立了对应的虚拟模型,融合飞行器的历史数据以及传感设备实时监测的数据,在虚拟世界中真实映射了物理对象的全生命周期过程[15-16]。达索公司构建了数字孪生3D体验平台,通过读取数字世界中用户反馈的数据,迭代优化信息空间的孪生模型,完善物理空间的物理对象[17]。德国西门子公司构建了生产系统的数字孪生模型,集成了工业设备制造过程,形成了基于模型的虚拟企业和基于自动化技术的企业镜像,支持企业在整个价值链上的整合和数字化转型,并将该模型应用于西门子工业设备纳米盒PC的生产过程中[18-20]。Schluse等人[21]将数字孪生技术应用于工业机器人研究中,为传统的设计、编程、控制和优化过程带来新的体验,简化开发过程且减少了生命周期中的仿真时间。
近年来,关于数字孪生模型与物理实体之间的研究主要集中于缓慢的交互过程,而对于在线数据的数字孪生实时修正方面的研究仍然鲜有报道。本文结合拉丁超立方全局搜索和贪婪局部搜索,提出实时自修正的数字孪生模型,利用位置的邻近性、形状的相似性和谱密度差异体现度量差异,从而实现物理实体与数字孪生体之间的一致性度量和数字孪生模型的动态修正。
1 问题概述
假设s和r分别表示数字孪生模型和物理实体,Us={us1,us2,…,usn}表示数字孪生的输出,Ur={ur1,ur2,…,urn}表示传感器获取的物理实体的实时输出。用C(Us,Ur)表示Us相对于Ur的一致性程度,且C(Us,Ur)∈(0,1]。当Us与Ur之间没有差异时,则仿真模型完全可信,有C(Us,Ur)=1;当Us与Ur之间差异较大时,则仿真模型不可信,有C(Us,Ur)→0。
假设di(i=1,2,…,m)表示数字孪生模型s的可调参数,其取值范围为λi。实时数据驱动的数字孪生模型的动态修正可转变为以下的优化问题:
maxC(Us,Ur), s.t.di∈λi,i=1,2,…,m
(1)
在数字孪生研究领域,存在q个对应的仿真模型Mi(i=1,2,…,q),也就是存在q组对应的数字孪生模型Usi。当系统存在多个输出时,通过寻求di和C(Us,Ur)两者之间的最佳映射关系,从已获取的可调参数集合di中选取最优参数。但是最佳的映射关系在现实中几乎难以实现,而且可调参数也存在一定的范围,无法一次性地找到最优解,选取的结果过于随机,所以在模型中以差异值代替关系映射来选取参数。
2 一致性度量模型
为实现对物理实体的精准映射,需要建立精准反映数字孪生模型与物理实体差异的一致性度量标准。为此,本文基于数据变化速率,将模型分为渐变模型和快变模型等2类[22],并分别应用位置差异、外形差异以及谱密度差异等差异计算方法构建孪生模型和物理实体的一致性度量模型。
令u=〈u(1),u(2),…,u(N)〉为一个时间序列数据,时间用t(i)表示,u(i)为按时间顺序得到的数据,定义u的数据变化快慢如下所示:
(2)
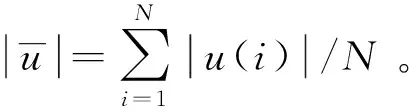
设置f为数据变化快慢的临界值,如果F≤f,可认为u为渐进变化的数据;反之,则认为u为快速变化的数据。
2.1 渐变数据的一致性度量模型
如果物理实体和数字孪生体的输出是渐进变化的数据,定义如下:
H=〈h(1),h(2),…,h(t)〉
=〈us1-ur1,us2-ur2,…,ust-urt〉
(3)
若h(1),h(2),…,h(t)彼此接近,则us和ur的形状类似,尤其当us和ur重合或平行时,有h(1)=h(2)=…=h(t)。
利用位置差异es和外形差异et来刻画渐变数据的差异[19],给出定义如下:
(4)
(5)
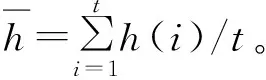
2.2 快变数据的一致性度量模型
如果物理实体和数字孪生的输出是快速变化的数据,分别为Ur={ur1,ur2,…,urn}和Us={us1,us2,…,usn}。
由于快速变化的数据包含反映波动特征的平稳分量和反映变化趋势特征的趋势分量,本文基于经验模态分解算法对其进行分离[23],得到平稳项和趋势项。趋势项利用渐变数据的位置差es和外形差et来刻画。

3 自修正方法构建
如第1章所述,可调整参数di存在一定的取值范围,无法通过求值法得出集合中的最优解,并且通过求解某一方程来直接求得di是不现实的。本文通过采用搜索法代替非求解法来优化参数的求解过程,避免了直接求取C(Us,Ur)和di两者之间数学映射的难题。在搜索求解过程中,选用拉丁超立方抽样试验方法将可调参数进行向量表示,并结合一致性度量模型,寻找全局和局部最优参数解。在参数选择过程中,引入迭代机制,实现参数解的实时动态更新,改善参数范围过于随机性问题,以优化过程替代选取过程,以此确保参数选取的可靠性。
参数快速搜索的流程如图1所示。

图1 参数快速搜索流程图
本章构建一种数字孪生模型的自修正方法,将参数的直接计算问题转化为参数选取问题,并结合拉丁超立方全局搜索和局部贪婪搜索消除参数选取的随机性,采用迭代取值验证参数动态调整的可靠性,最终获取最优的可调控制参数解。方法的具体实现过程和步骤如下:
算法1 自修正方法实现过程
输入:可调参数di∈λi,仿真实体Ur,预设迭代步长S
输出:参数最优解z
初始化:z∈∅
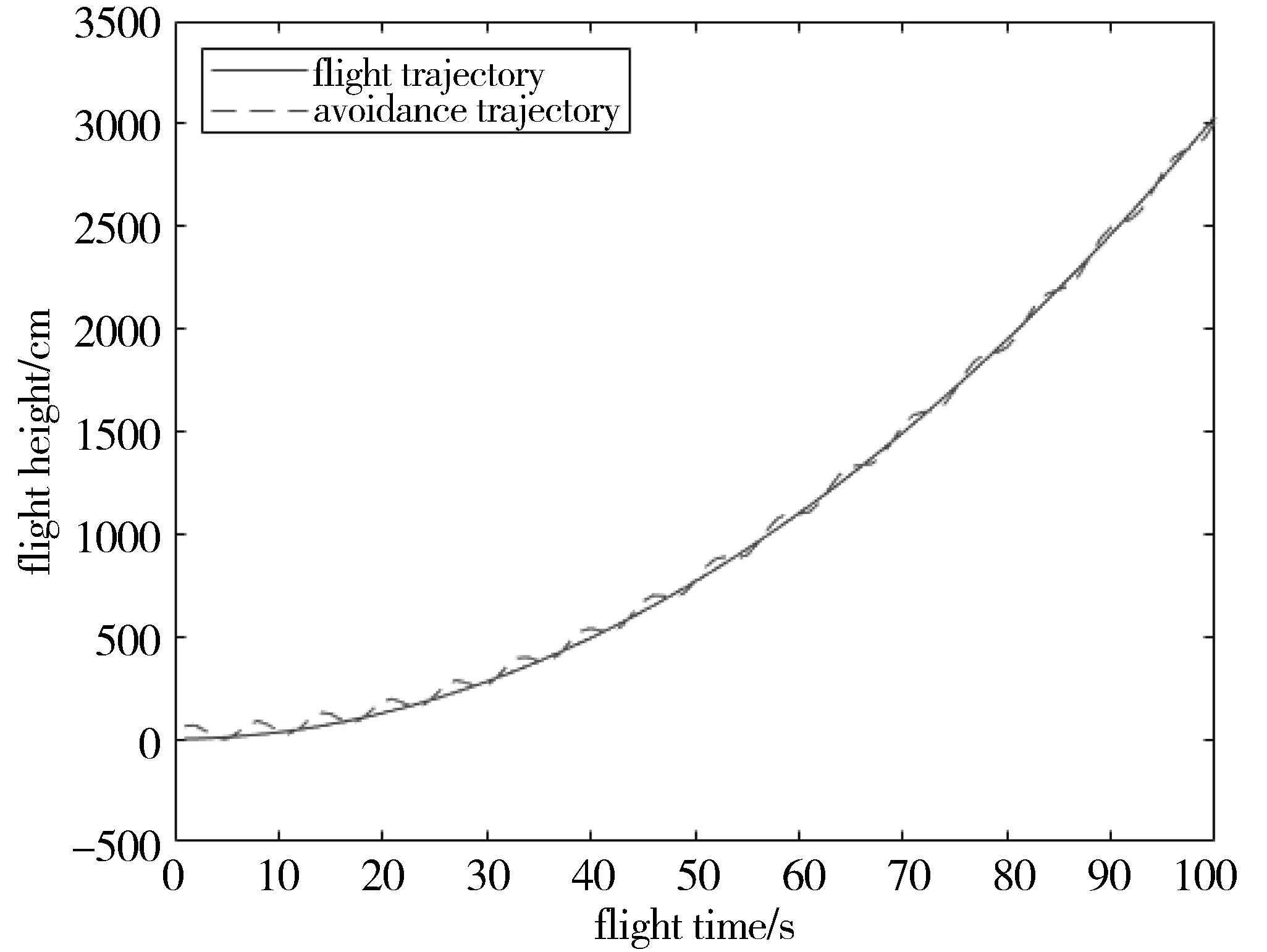
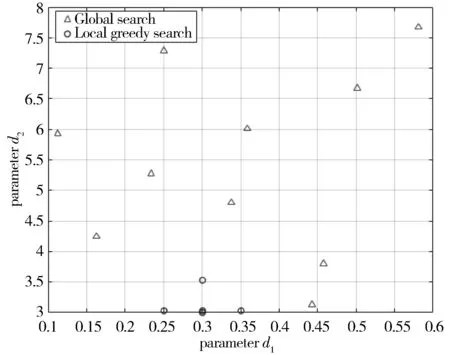
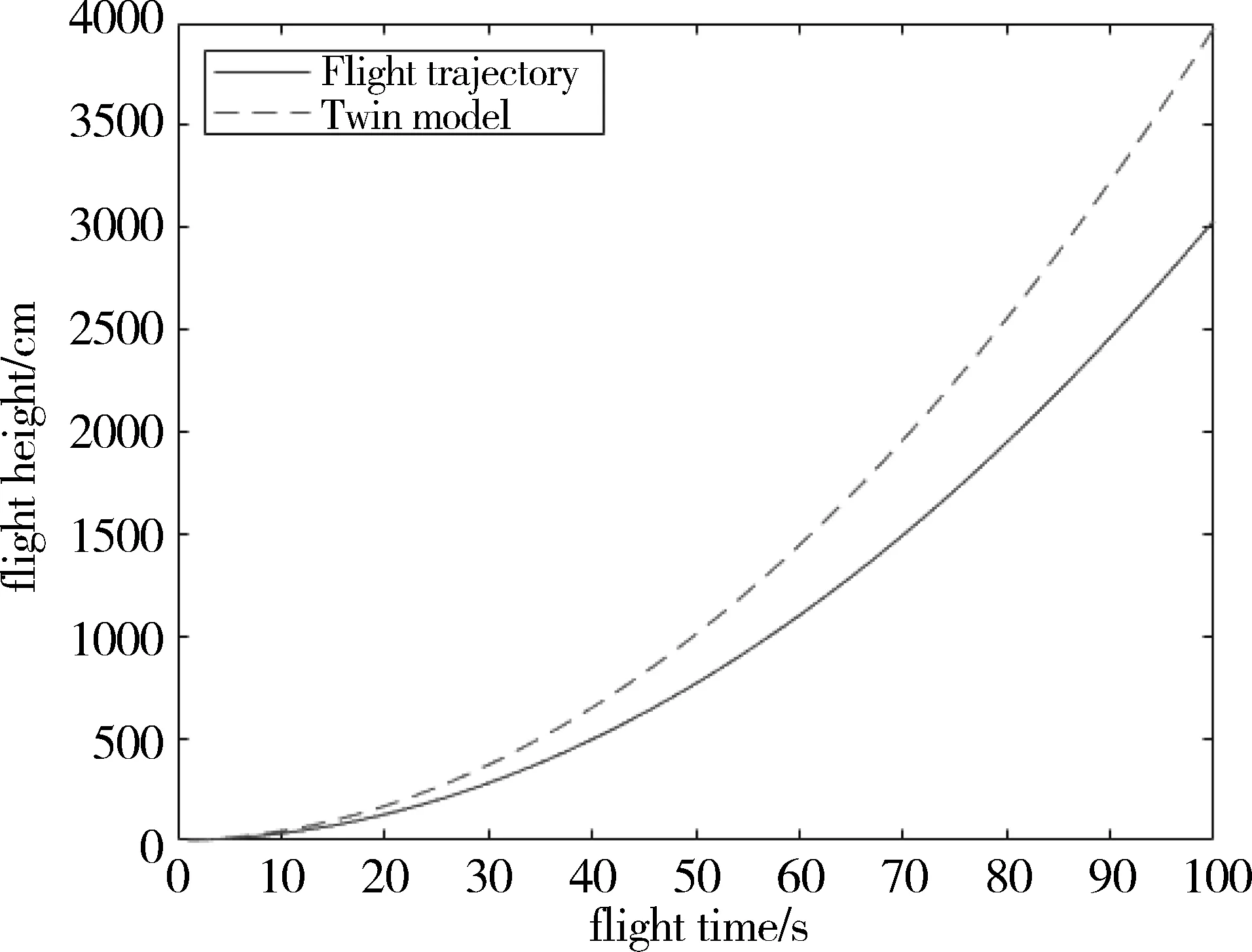
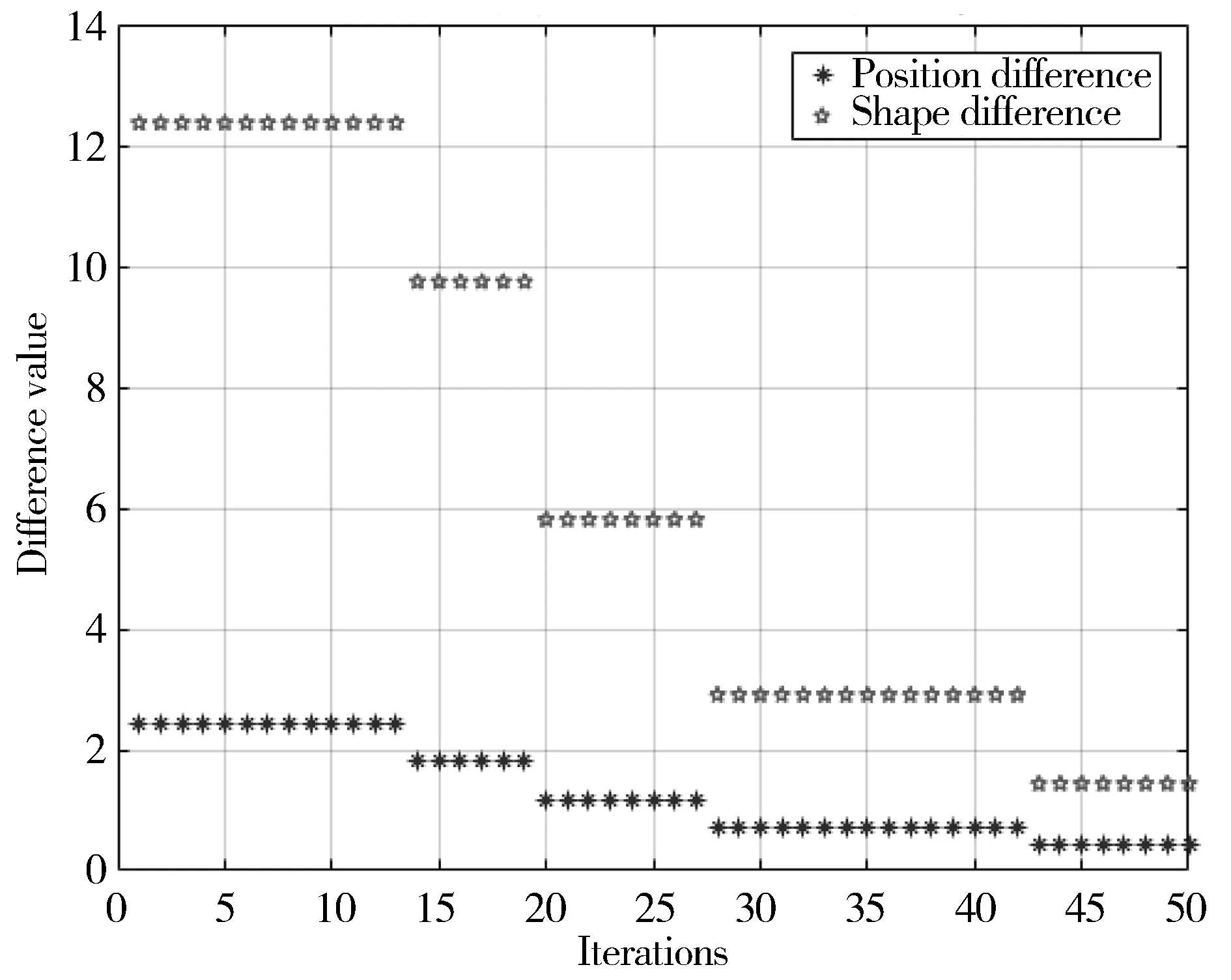
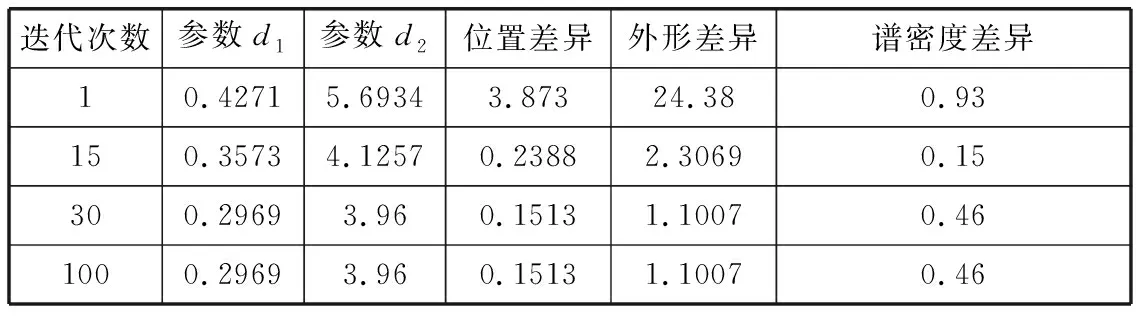
while Iteration 构建LHS矩阵 选取差异值最小的参数di z=z else end end Step1全局搜索。 (6) (7) (8) 式中,P{·}表示事件概率。 根据拉丁超立方抽样[26-28],建立一个拉丁超立方矩阵LHS(n,m),定义如下: (9) Step2一致性度量。 Step3局部贪婪搜索。 Step4参数自修正。 Step5迭代取值。 在预设的迭代次数内,依次循环执行Step1~Step4,循环结束时模型输出最优的参数解。 实验的仿真环境为Windows 10操作系统,处理器为Intel(R) Core(TM) i5-10400f CPU,主频为2.9 GHz,内存16 GB,仿真使用MATLAB2018b。针对某飞行器的实时飞行运动,获取其飞行状态下的实时运动轨迹数据,并将估计得到的飞行器进行规避动作的规避轨迹数据作为物理实体,如图2所示,现采用在线仿真的手段构建一个符合飞行运动轨迹的数字孪生模型。 图2 运动状态轨迹图 已知数字孪生模型中的飞行状态控制可调参数为d1∈[0.1,0.6]、d2∈[3,8],数据变化快慢的预设值为3。根据数据变化快慢,飞行运动轨迹的数据变化频率为2.9382,小于专家预设值3,代表其是渐变数据,飞行规避轨迹的数据变化频率为3.4079,大于专家预设值3,代表其为快变数据。 针对渐变模型,使用第3章的参数快速搜索方法,采用拉丁超立方矩阵表示的样本,得到了10组可调参数,包括5组并行计算量的局部搜索参数,共15组可调参数。样本参数如图3所示。 图3 渐变数据可调样本参数 模型根据预设不同的迭代次数,会得到相对应的参数解集合,由此得出差异如表1所示。 表1 不同迭代次数及参数解的渐变模型差异值 由表1看出,当迭代次数从1次增加至50次时,位置差异和外形差异迅速减小,而当迭代到100次时,不仅2个可调参数的数值保持不变,且孪生模型与仿真实体间的位置差异值及外形差异值均保持不变,这表明模型迭代到50次时,可调参数已取得最优值,此时控制参数的取值更加贴近仿真实体,与仿真实体间的差异降到最低。为了更加直观地显现差异,将模型在最优参数条件下的4次迭代实验结果绘制到曲线图中,具体如图4所示。 (a) Iteration=1 由图4可以看出,随着迭代次数的增加,代表渐变模型选取结果与飞行运动轨迹的2条曲线渐趋一致,这表明模型选取性能在不断优化。由图可知,迭代1次时,渐变模型与物理实体2条曲线存在肉眼可见的差异,这表明此时两者的匹配程度不理想;当迭代到30次时,渐变模型与物理实体的差异值在迅速减小,两者之间的匹配度有了明显提高;当迭代次数提高到50时,2条曲线几乎重合,这说明两者的匹配程度有了进一步的提升。然而,当迭代次数为100时,相较于迭次50的结果,模型的选取结果没有变化,这表明渐变模型在迭代到50次时已经达到最理想的选取效果。因此,本文渐变模型的迭代次数设置为50。其中最优参数的迭代差异值如图5所示。 图5 渐变模型最佳可调参数的迭代差异 由图5可以看出,当迭代次数不断增加,渐变模型和仿真实体的位置差异值和外形差异值呈阶梯下降趋势,两者之间差异值的总值是随着迭代次数在逐渐减少,这说明渐变模型和仿真实体的整体差异是在减少的。通过计算,模型迭代到43次时,渐变模型和物理实体的位置差异和外形差异值的和最小,说明此时两者之间的差异最小,且最优参数解的搜索结果可以被接受,即0.3~0.3005和3.5~3.5312。实验表明本文方法能够通过不断调整渐变模型,找到一个使得差异值最小的控制参数解。 针对快变模型,搜索方法与渐变模型相同,采样参数如图6所示。 图6 快变数据可调样本参数 根据不同的迭代次数,得到不同的最优参数解,分别得出差异如表2所示。 表2 不同迭代次数的快变模型差异值 由表2可看出,当迭代次数逐渐变化为30时,2个可调参数d1、d2取得0.2969和3.96,与规避轨迹对应的位置差异、外形差异和谱密度差异值取得最小,这表明可调参数取值已取得最优值。而当迭代次数超过30时,2个可调参数无任何变化,处于稳定状态,进一步验证迭代到30次取得的2个可调参数为模型最优解。利用已取得的最优解,孪生模型在不同迭代次数条件下的选取结果如图7所示。 (a) Iteration=1 图7显示,参数选取的合理性与模型迭代次数呈正相关变化,最终导致快变模型的选取结果与规避轨迹的相似度也越来越高。从图中可以看出,当迭代次数为1时,快变模型与物理实体之间的差异较大,符合度不高;而当迭代次数调整为15时,快变模型与物理实体的差异值在迅速缩小,符合度较高;最终当迭代次数增长至30时,两者的差异值显著减少,曲线图中代表两者的曲线几乎重合,符合度达到最高。然而,相似度并不是随着迭代次数的增加无限增长,实验中选取的迭代次数为100时验证了这一点,不仅最优参数选取结果不变,快变模型和物理实体的差异值也没有变化,且模型寻找最优参数解的时间复杂度更高。故在本次实验中,快变模型选取30作为迭代次数。其中最优参数的迭代差异值如图8所示。 图8 快变数据最佳可调参数的迭代差异 图8表明,随着迭代次数不断增加,快变模型和仿真实体的外形和位置差异值均在逐渐减小,而谱密度差异值在迭代到23次时虽呈上涨趋势,但是从3个差异角度的总体来考虑,迭代23次之后,单一要素谱密度差异值的变化值远远小于外形和位置差异这2个层面的变化值,以3个层面的差异值的累加值作为参考,快变模型和仿真实体两者之间的整体差异总体还是在减少。从散点图中可以看出,迭代到30次时,位置差异值接近0,位置差异与谱密度差异值也保持稳定,此时3个差异值的和取得最小值,表明快变模型和仿真实体的差异值达到最小,并且最优参数解的搜索结果可以被接受,即0.2969~0.3和3.96~4。 针对数字孪生模型参数选取过于随机问题,考虑飞行状态控制参数存在一定取值范围,本文提出了一种孪生模型可调参数优化方法,构建了孪生系统的一致性度量模型,充分刻画了仿真实体和孪生模型两者之间的度量差异。在基于LHS试验方法中,将直接计算问题转化为参数选择问题,消除参数选取的随机性,并结合迭代取值对孪生模型进行可信性验证,得到最优的控制参数解和数字孪生模型。本文结合了拉丁超立方全局搜索和局部贪婪搜索,使可调参数搜索具备时效性和可靠性。实验结果表明,采用参数快速搜索方法,优化了可调参数求解的过程,实现了孪生模型与仿真实体之间的动态联动融合与优化和模型参数的动态调整,满足数字孪生模型实时动态修正的需求。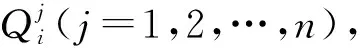
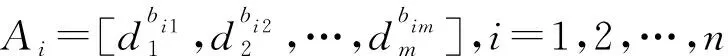



4 仿真实验




5 结束语

