控制棒落棒时间分析软件CRAC的研发与验证

马 超，周 毅，卢嘉川，芦 韡，李 云，赵 波，陈 浩，马 强，秦 勉，郭晓明

(中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610213)

压水堆紧急停堆时，控制棒组件依靠重力下落控制反应性，实现安全停堆。落棒时间计算是反应堆安全分析和燃料组件及相关组件设计的重要部分，关系到导向管及控制棒设计是否满足落棒时间准则。针对落棒开展理论研究，研发落棒时间的分析工具，获得落棒位移-速度-时间关系，对反应堆安全分析及燃料组件设计具有重要意义。

针对压水堆落棒时间分析技术，国内外研究者开展大量研究工作，通过试验与理论分析，认为落棒过程中控制棒驱动线受到的载荷主要为水力阻力和机械阻力。针对机械阻力，研究者利用有限差分或有限元法，求解驱动线各部件的振动方程，通过设置表面接触条件，计算控制棒受到的非线性碰撞力与摩擦力[1-2]。水力阻力具体包括浮力、惯性力、局部形阻力和沿程阻力。针对水力阻力，研究者利用流体力学理论和经验公式相结合的方法计算落棒过程中流体阻力[3]，还有研究者利用CFD软件动网格技术，开展落棒过程中水力缓冲模拟[4-7]。上述研究工作考虑的落棒模型较为简单，仅围绕某一种载荷建模，如控制棒所受水力阻力或机械阻力，忽略或简化考虑其他载荷因素，距离工程应用较远。动网格技术需要耗费大量计算资源，只能构建简单控制棒结构的仿真模型，如单根控制棒和水力缓冲部件，无法开展全尺寸控制棒驱动线模拟。

国内外核电企业采用理论和经验关系式相结合的方式求解落棒过程中的水力阻力和机械阻力[8-10]，在试验数据基础上，形成针对特定堆型的落棒专用程序，开展落棒时间计算。本文介绍适用于华龙一号工程设计的落棒时间分析程序CRAC，满足华龙一号落棒时间分析需求。

1 CRAC功能

CRAC通过合理简化控制棒驱动线结构与载荷形式，建立动力学方程，基于流体力学压降平衡关系、弹簧胡克定律及经验机械阻力关系，求解落棒过程中的流体阻力与机械阻力，获取反应堆正常工况及地震停堆工况，落棒总体时间及随时间变化的控制棒位移、速度信息，适用于华龙一号控制棒驱动线的落棒时间计算。

2 理论模型

2.1 总体理论模型

控制棒驱动线结构如图1所示，导向通道在轴向由下至上分为3部分：堆芯燃料组件部分、导向筒部件部分和控制棒驱动机构部分。反应堆正常运行状态下，上部的驱动机构钩爪提升驱动杆，将控制棒组件大部分停留在堆芯外部，控制棒棒束保持在导向筒部件中；需要停堆时，钩爪部件断电，松开驱动杆，控制棒驱动线依靠重力下落到燃料组件中，实现停堆。驱动杆、控制棒为细长结构(长径比大于100∶1)，控制棒驱动线与通道之间间隙较小，限制了径向运动，因此在分析落棒过程中，近似为一维轴向运动。

图1 反应堆控制棒驱动线结构Fig.1 Structure of reactor control rod drive line

图2示出控制棒驱动线受力示意图，针对控制棒轴向运动建模，所有作用力都作用在重心，建立运动方程如下：

图2 控制棒驱动线受力示意图Fig.2 Force analysis schematic of control rod drive line

(1)

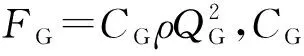
2.2 流体阻力计算模型

控制棒在驱动机构、导向筒及燃料组件3部分通道中运动。由于在导向筒中流场较为宽阔，水力阻力较小，故忽略导向筒内作用在行星架与控制棒上的水力阻力。运动部件所受流体阻力，主要考虑控制棒在燃料组件中及驱动杆在驱动机构中受到的流体阻力。引入如下假设：1) 流体不可压缩；2) 落棒过程中在燃料组件导向管和缓冲段内的水温为常数；3) 在每个计算时间步内，固定壁面摩擦系数与运动壁面摩擦系数为定值(两者选取不同参考速度)。

2.2.1控制棒在燃料组件内所受到的水力阻力 图3示出控制棒插入到导向管和缓冲段示意图，采用集总参数法描述流道速度信息，如表1所列。由于堆芯流量可能在较大范围内变化及控制棒组件机械缓冲回弹现象存在，各流道速度方向可能发生变化。在水力阻力建模前，需定义速度标志位，保证对流体动力学方程求解的正确。

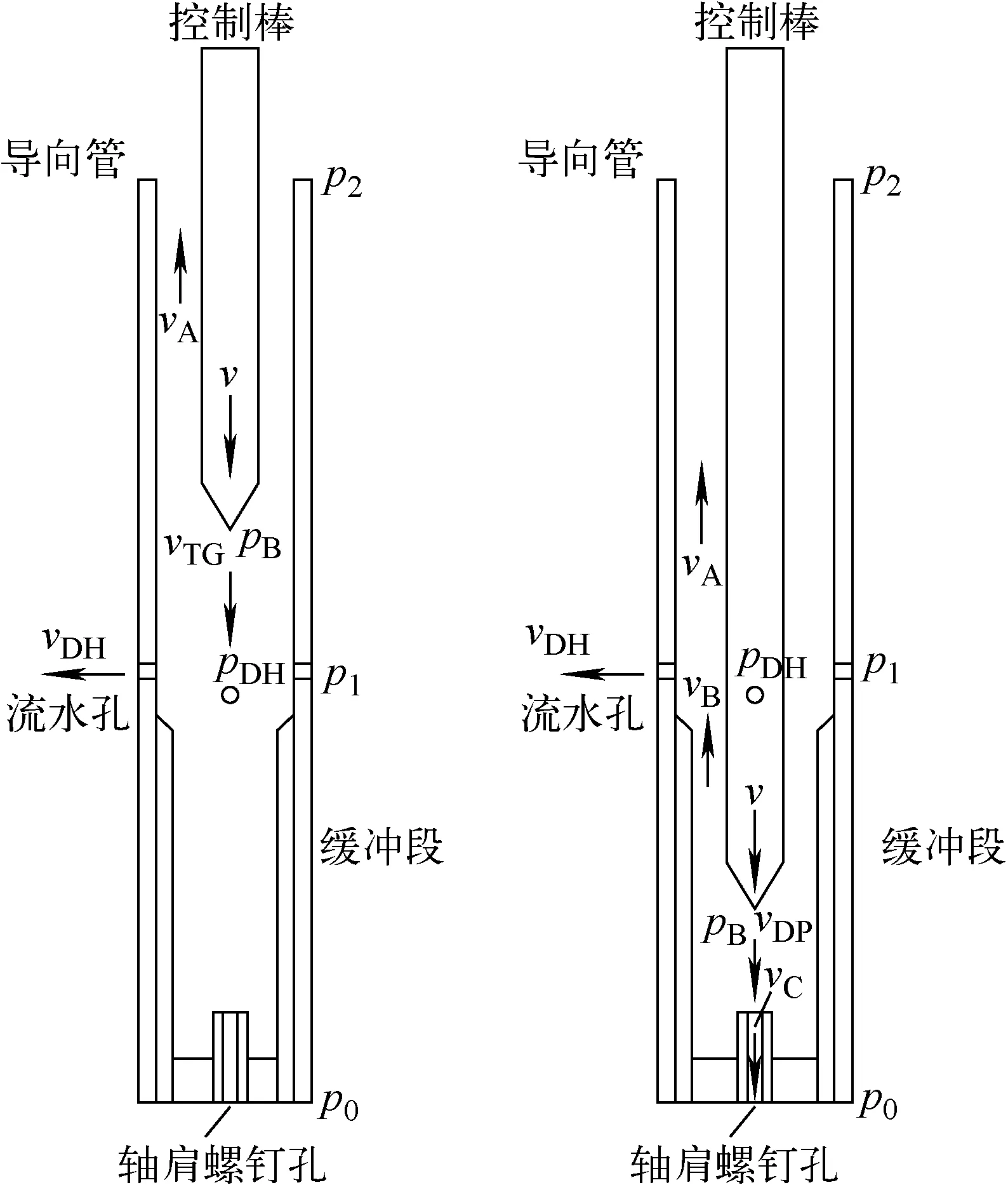
图3 控制棒插入到导向管和缓冲段示意图Fig.3 Schematic of control rod dropin thimble guide and dashpot

表1 各通道流体速度定义Table 1 Definition of fluid velocity direction in different flow channels

1) 控制棒在导向管内运动

在燃料组件中所受水力阻力，由压差引起的作用力和沿程阻力组成：

FFA=NCR(SCR(pB-p2)+lABCRτCR)

(2)

式中：FFA为控制棒组件在燃料组件内受到的水力阻力；NCR为控制棒组件中棒总数；SCR为单根控制棒横截面积；pB为控制棒下端界面处压强；p2为导向管顶端外部压强；lA为控制棒插入导向管轴向长度；BCR为单根控制棒湿润周长；τCR为控制棒在导向管内受到的平均流体切应力。

连续性方程为：

vSCR-vASA-4vDHSDH=0

(3)

4vDHSDH=vTGSTG

(4)

式中：STG为导向管圆形通道过流面积；SA为导向管环形通道过流面积；SDH为单个流水孔过流面积(周向分布共4个)。流水孔外侧和控制棒下端之间的流体压差为：

(5)

式中：p1为流水孔外侧的流体压强；ξDH为流水孔局部阻力系数；λTG为导向管圆形通道的沿程阻力系数；DTG为导向管通道水力直径；lTG为导向管总长度。

在导向管环形通道内，控制棒下端与导向管上端之间压差表示如下：

(6)

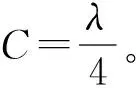
λ按Colebrook公式计算[11]：

(7)

式中：Ks为壁面绝对粗糙度；Re为雷诺数，Re=vrefDρ/η，vref为参考速度，η为流体黏度；D为水力直径。

从流水孔外侧到导向管顶端压降Δp12=p1-p2，由燃料组件特性、进入燃料组件流量及流体温度共同确定，因此Δp12视为已知量，根据压降平衡关系：

Δp12=(p1-pB)+(pB-p2)

(8)

在确定每一时间步v(t)条件下，联立式(3)～(6)及(8)可确定vA(t)，从而确定当前时刻控制棒压差(pB-p2)和切向应力分量：

(9)

根据式(2)获得控制棒受到的水力阻力FFA。

2) 控制棒在缓冲段内运动

当控制棒插入缓冲段时，控制棒组件受到的水力阻力FFA由式(10)计算，此时导向管内环形流道长度为lA=lTG。

(10)

式中：lB为控制棒插入缓冲段内长度；CCRB为缓冲段环形流道中控制棒壁面摩擦系数。此时，连续性方程如下：

4vDHSDH+vASA-vBSB=0

(11)

vSCR+vDPSDP+vBSB=0

(12)

式中：SB为缓冲段环形流道过流面积；SDP为缓冲段圆形流道过流面积。控制棒下端与导向管顶端之间压降分为两段：

(13)

(14)

式中：pDH为流水孔内侧流体压强；CDP为环形流道缓冲段壁面侧摩擦系数；ξ1BS为环形流道截面突然扩张的局部压力损失系数，即从SB突扩至SA的压力损失系数。由导向管缓冲段对应的外部流道压降平衡关系为：

pB-pDH=(pB-p0)+

(p0-p1)+(p1-pDH)

(15)

式中，p0为轴肩螺钉阻尼孔底端压力。

(16)

(17)

式中：lDP为缓冲段总长；λDP为缓冲段圆形通道沿程损失系数；λSH为轴肩螺钉阻尼孔中沿程损失系数；DDP为缓冲段圆形通道水力直径；DSH为轴肩螺钉孔水力直径；lSH为轴肩螺钉孔深；ξSH为轴肩螺钉阻尼孔局部压力损失系数；SSH为轴肩螺钉孔过流面积。因此式(15)可转化为：

(18)

式中，Δp01=p0-p1视为已知。

在已知v(t)情况下，联立式(13)、(14)、(16)和(18)可确定vA(t)、vB(t)，进而确定压差(pTG-pA2)，通过式(10)计算控制棒插入缓冲段时受到的水力阻力FFA。

2.2.2驱动杆在驱动机构内受到的水力阻力 驱动杆在驱动机构中受到的水力阻力建模过程与2.2.1节内容相似，通过求解连续性方程和动力学方程，可得驱动杆受到的水力阻力FCRDM。

2.3 机械阻力计算模型

在控制棒驱动线落棒过程中，驱动杆与控制棒会发生变形，与导向通道发生随机碰撞接触，机械运动行为复杂，直接针对驱动线相关设备结构形式建模，计算模型将非常庞大且求解困难。因此在CRAC研发过程中，考虑基于控制棒驱动线相关试验结果与工程经验，建立机械阻力相对于错对中量及插入深度变化的计算模型：

Ff=F(d,z)+F0

(19)

式中：函数F(d，z)输入变量包括上部导向组件与隔热套之间错对中量d及落棒位移z，F(d，z)是在参考试验数据条件下，考虑工程保守性建立的插值函数；F0为对中条件下的机械摩擦力。

3 CRAC计算流程

图4示出CRAC计算流程，通过输入整个系统初始参数，包括结构尺寸参数、冷却剂物性参数、控制棒初始位置与速度、各通道中流体初始速度和压强，确定控制棒驱动线初始加速度。将时间步长设为Δt，第i时间步对应时刻ti=ti-1+Δt，该时刻所有载荷与流体状态将根据时刻ti-1的特性确定。每一时间步求出控制棒驱动线所受合力，求得加速度及其他下落特性参数。重复上述过程，直至控制棒组件完全插入燃料组件，实现对落棒过程的模拟计算。

图4 CRAC计算流程图Fig.4 Calculation flow chart of CRAC

4 CRAC验证

4.1 落棒试验简介

CF2燃料组件是由中国核动力研究设计院自主设计研发，是第三代核电华龙一号核心部件。为满足第三代核电燃料组件刚度要求，CF2在导向管缓冲结构方面采用管中管新型设计。该燃料组件将应用于华龙一号国外首堆巴基斯坦卡拉奇2号机组的首循环。本次落棒试验中回路参数为：压力15.5 MPa，温度315 ℃，工况列于表2[12]。试验测量得到：控制棒下落至缓冲段入口的落棒时间(T5)；控制棒下落至全插入位置的落棒时间(T5+T6)；控制棒下落速度、位移与时间关系。落棒时间测量误差为±0.01 ms，落棒速度测量系统相对误差为±0.28%。

4.2 计算结果与试验值对比

根据试验条件及控制棒驱动线结构参数，利用CRAC进行表2所列5种工况下的落棒模拟计算。图5示出G1和G5工况下速度-时间和位移-时间曲线。由图5可知：CRAC计算结果与试验结果变化趋势一致，但计算最大速度值要比试验值略低；CRAC计算的位移曲线趋势较为平缓，落棒时间结果要比试验值大。因为CRAC中机械摩擦阻力及水力局部压降系数均为经验函数或经验系数，充分考虑落棒时间计算保守性，保证软件计算值大于真实值。

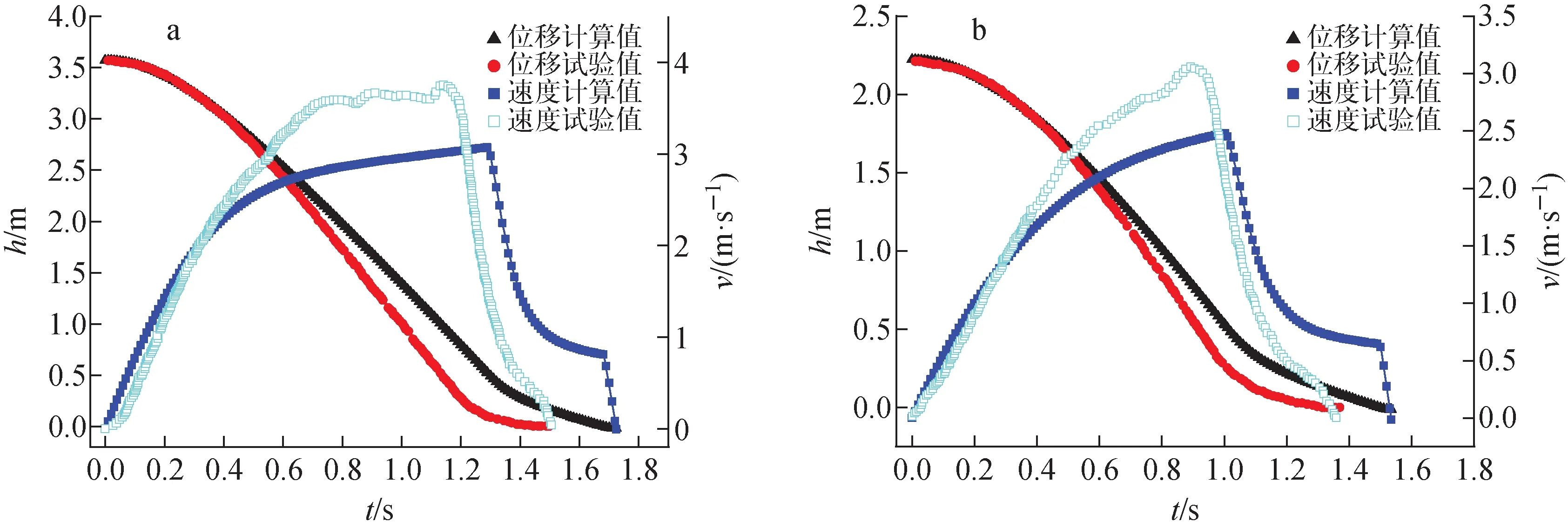
图5 工况G1(a)、G5(b)条件下的落棒结果对比Fig.5 Comparison of control rod drop result for G1 (a), G5 (b) conditions

表2 落棒试验工况Table 2 Condition of drop experiment

落棒试验获得的速度曲线在控制棒进入缓冲段之前达到最大，此时曲线出现明显的突然上升、然后下降过程。产生该现象的可能原因是，控制棒下落的过程中，子弹头部位会产生局部过压，在导向管中运动过程中，距离流水孔较远时，过压产生的水力阻力压差增大较为平缓连续，而在控制棒子弹头接近流水孔时，流水孔处内外压差较大，流水孔起到泄压作用，使得控制棒子弹头部位过压在流水孔附近产生先降低(泄压)再升高(进入缓冲段)的变化，因此速度曲线在此处先迅速升高再迅速下降。由于CRAC采用一维集总参数模型，将控制棒简化为圆柱体，无法考虑子弹头部位的压力场与速度场急剧变化现象，因此获得的速度-时间曲线是逐渐变化，没有突然上升再下降的过程。

表3列出试验数据(T5，T5+T6)与计算结果对比，计算值均大于试验值，实现对试验数据的包络，满足反应堆安全分析保守性要求。落棒时间计算值同试验值符合性较好，最大相对误差为15.45%，证明CRAC对华龙一号堆型落棒时间计算的适用性以及准确性。

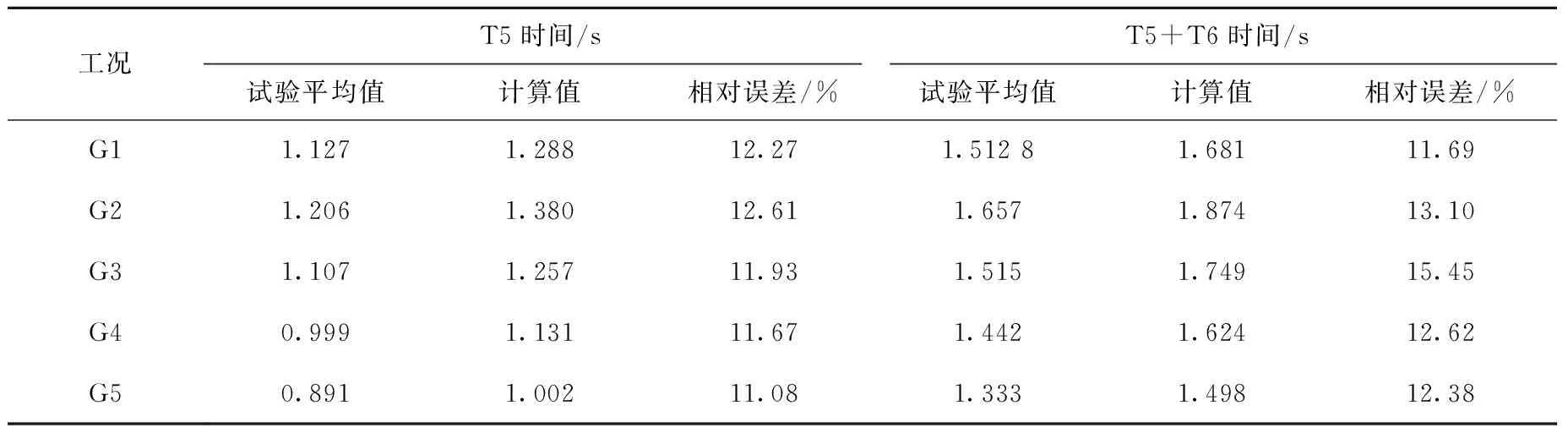
表3 落棒时间计算与试验数据对比Table 3 Comparison of calculated and measured values for control rod drop time

5 结论

本文介绍了CRAC的功能、理论模型、计算流程，并利用试验数据对CRAC的计算准确性进行验证，计算结果与试验数据相对误差在15.45%以内，两者符合较好，且计算结果均大于试验结果，表明软件计算精度与保守性能满足华龙一号堆型安全停堆时间准则分析需求。