高温热管内钠蒸发冷凝特性分子动力学研究

汪泽涛，郭凯伦，王成龙，张大林，田文喜，秋穗正，苏光辉

(西安交通大学 核科学与技术学院，陕西 西安 710049)

热管堆以紧凑性、非能动性、高效性等优势，在未来有广泛的应用场景[1]。热管在堆内热量传输方面发挥着关键作用。热管堆多采用钠、钾、锂等液态金属工质的高温碱金属热管，其工作温度较高，相关热力学参数测量具有一定难度，开展实验对工质相变换热机理进行研究具有一定困难。同时，由于液态金属相变换热等机理现象尚不确定，用CFD方法直接模拟液态金属蒸发过程难度较大。

分子动力学[2]作为一种微观模拟手段，在工质的蒸发冷凝现象的机理研究中已有诸多应用[3-5]，有望成为研究高温热管内工质相变特性的有力工具。本文采用分子动力学软件LAMMPS，结合钠热管启动阶段的运行工况[6-7]，模拟600 K下钠的蒸发过程，对比了两种质量调节系数的统计方法，随后进行非平衡态模拟，求解净蒸发通量、交界换热系数，并探讨影响钠蒸发的有关因素。

1 蒸发理论

蒸发是一种常见的自然现象，被广泛应用于诸多领域。从微观来看，蒸发是气液交界处气液相分子间的净输运过程。130多年来，学术界普遍使用HK模型研究该过程，后基于该模型，进行改进，又提出了Schrage模型、Tsuruta模型等[8]。图1示出气液交界的蒸发与冷凝，内含蒸气温度为Tv、饱和压力为pv的饱和蒸气与液相温度为Tl的液体。分子运动理论认为，气液交界的传质，是凝结通量与蒸发通量之间的竞争过程：前者大于后者，发生凝结；后者大于前者，发生蒸发。二者之差视为净蒸发通量。平衡态下，净蒸发通量理论上为0，但实际中该值为一个接近0的微小值。

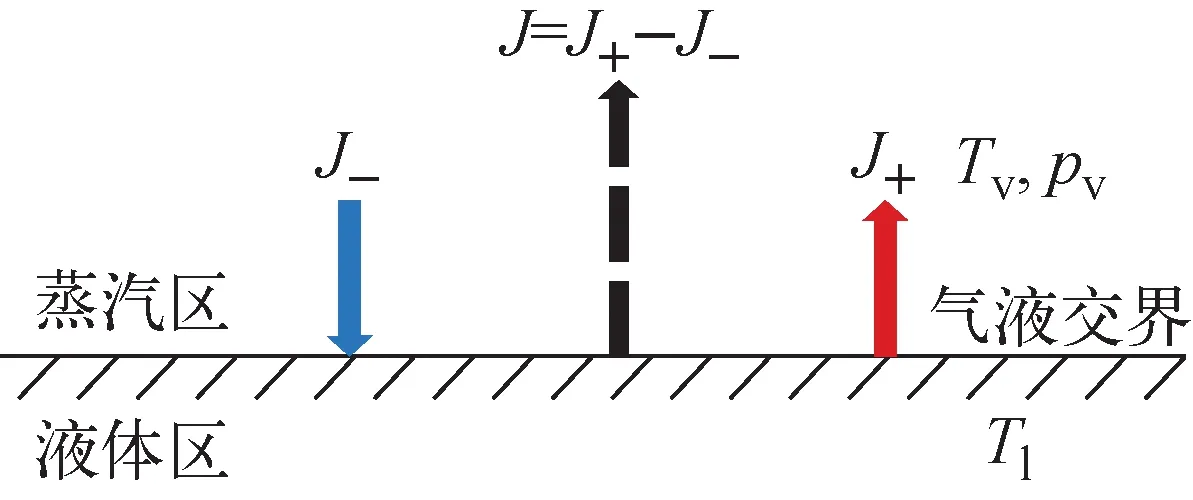
图1 气液交界的蒸发与冷凝Fig.1 Evaporation and condensation at liquid-gas interface

Schrage[9]认为在气液交界的相变过程中，并非所有与交界接触的分子都会被凝结，蒸气的净运动也会对凝结通量产生影响，通过添加修正因子，提出Schrage关系式计算净蒸发通量。在热管模拟中，该式可被用于确定吸液芯孔洞内气液交界的蒸发速率及后续的热阻网络计算：

(1)

式中：R为气体常数，J·mol/K；M为摩尔质量，kg/mol；pl为Tl对应下的蒸气压力，Pa；Γ为修正因子；αc、αe分别为凝结系数和蒸发系数，是指凝结分子通量、蒸发分子通量占总的碰撞交界的分子通量的比例。根据动态情况下并不严格成立的热静平衡的论证[10]，在实际应用中将两个系数视为相等，即α=αc=αe，本研究也采用了这一假设，并使用更为通用的质量调节系数[11](MAC)来命名α。在以往的高温热管模拟研究中，通常按经验，将该系数视为1[7]，该做法可能使热管模拟结果出现误差，进而影响热管的设计制造，对热管堆的正常运行造成不利影响，因此有必要从微观机理角度出发，对该系数进行深入研究。

2 模拟方法

2.1 模型设置

图2为模拟区域示意图。如图2所示，用LAMMPS软件建立尺寸为8.4 nm×8.4 nm×50.4 nm的模拟区域(微观角度出发，不同于传统宏观建模)，上、下侧各铺设9层金原子，最外侧1层为固定壁面，底部、顶部剩余8层分别作热源壁面、冷源壁面。热源壁面、冷源壁面上铺设钠薄膜(初始厚度为4 nm)。原子晶格形式均采用FCC(面心立方)，晶格常数分别为4.08、5.94[4]。x、y向采用周期边界，z向采用固定边界。

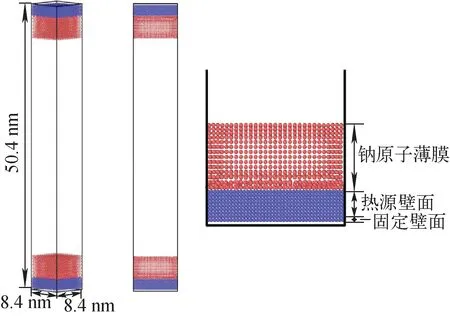
图2 模拟区域示意图Fig.2 Picture of simulation zone

原子间相互作用势选取12-6 Lennard-Jones(LJ)势[2]，分布形式如图3所示。该势的计算公式如下：

图3 12-6 LJ势函数图Fig.3 Picture of 12-6 LJ potential function

(2)

式中：φi,j为两原子间的相互作用势；r为两原子之间的相互距离；ε为势阱深度，指两原子间相互吸引作用的最大值；σ为特征长度，指两原子间不存在相互作用的距离。Na-Na、Au-Au、Na-Au间的势参数[12-14]选取列于表1。

表1 原子势参数Table 1 Atomic potiential parameter

2.2 模拟过程

步长设为1 fs。整个体系先在NVT(正则系综)下运行6 ns，以达到600 K平衡态，随后，为采集平衡态数据来统计质量调节系数，在NVE(微正则系综)下运行1 ns。最后，进行非平衡态模拟，钠原子继续处在NVE下，同时利用NVT将热源壁面、冷源壁面分别变温至720、520 K，运行20 ns。用MATLAB、OVITO进行后处理和可视化演示。

2.3 数据处理方法

当前采用分子动力学方法统计质量调节系数时，主要有Liang等[15]与Yu等[3]提出的两种方法，两方法的示意图如图4所示。Liang方法中，在距气液交界为3.2σNa-Na位置处，设定虚拟面，一定数目的气相原子穿过虚拟面，到达气液交界后会发生3种行为[16]：冷凝、冷凝后又蒸发、被交界面反弹(图5)。设定特征时间Δt(式(5))，规定Δt(约为11.16 ps)内，这些原子中重新穿回虚拟面的被视为反弹原子，通过统计反弹分子比例，继而得到冷凝分子比例，该比例即质量调节系数，如下式。

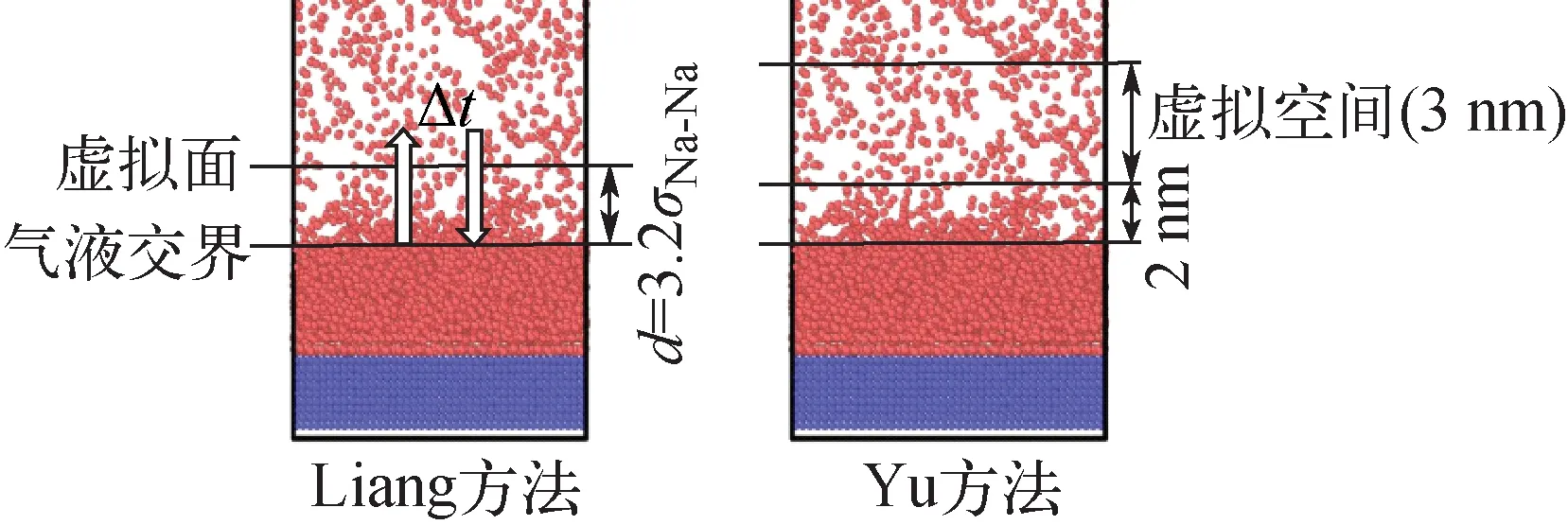
图4 统计方法示意图Fig.4 Picture of statistic method

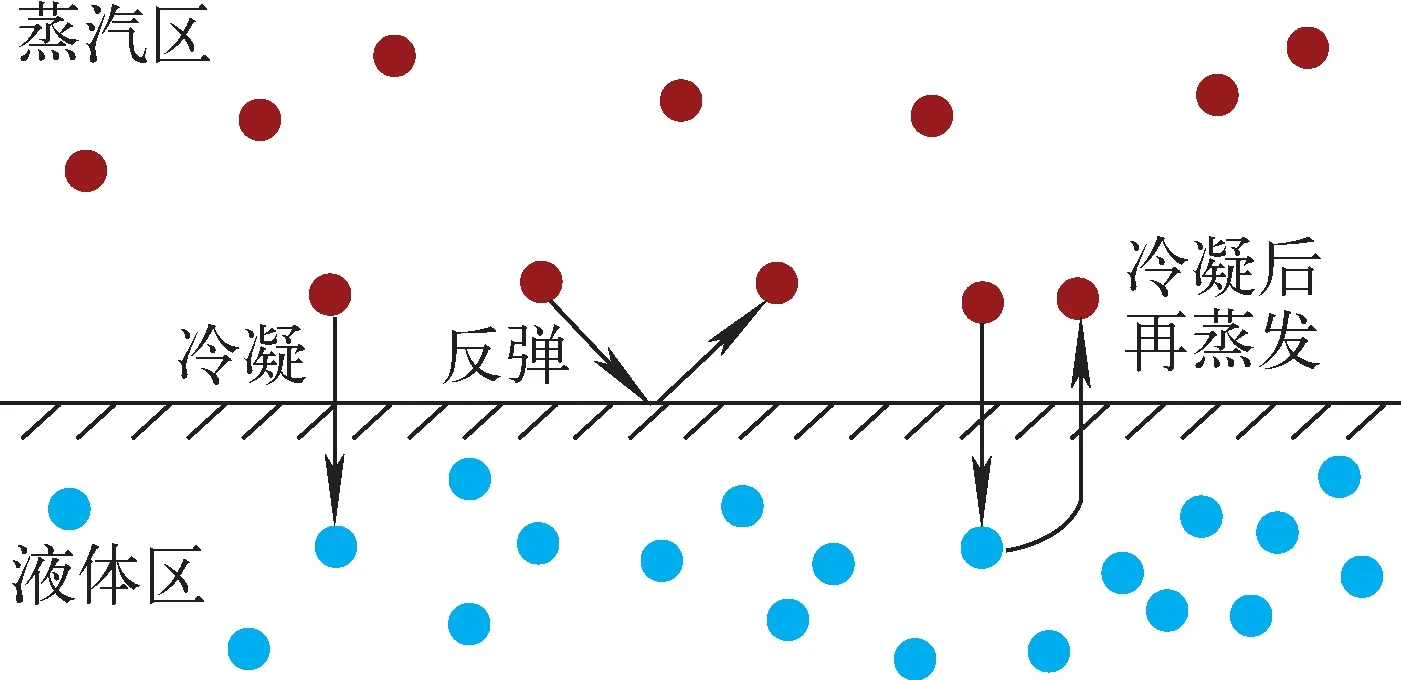
图5 气相原子在气液交界的3种行为Fig.5 Three behaviors of gas atoms at liquid-gas interface d=3.2σNa-Na

(3)

(4)

Δt=2d/um

(5)

α=1-Nref/N

(6)

Yu方法中，在临近气液交界位置(按Yu的设定，取2 nm)，设定高度3 nm的虚拟空间，通过追踪该空间内部原子在一段时间(能使虚拟空间内原子能运动至交界处，且在交界发生上述3种行为即可)内的位置信息，确定出冷凝分子数Ncond，得到质量调节系数α。

(7)

交界换热系数h使用下式[7]计算：

h=q/(Tv-Tl)

(8)

其中，q为热流密度，kW/m2，计算式[7,17]为：

q=Jhfg

(9)

hfg=Δhv(Tv)-Δhl(Tl)

(10)

Δhl(Tl)=-365.77+1.658 2T-

4.239 5×10-4T2+1.478 7×

10-7T3+2 992.6T-1

(11)

Δhv(Tv)=393.37(1-Tv/Tc)+

4 398.6(1-Tv/Tc)0.293 02+Δhl(Tv)

(12)

式中：hfg为汽化潜热，kJ/kg；临界温度Tc=2 503.7 K；Δhl(Tl)、Δhv(Tv)分别为对应温度下相对于298.15 K条件下时固态钠的焓增量，kJ/kg。

求解净蒸发通量采用上述Schrage关系式，中高温条件下，修正因子Γ[7]为：

(13)

(14)

ρv=pvM/RTv

(15)

根据以上3个公式和式(8)、(9)可得：

(16)

3 势参数验证

图6为竖直方向模拟所得密度与参考值的对比。如图6所示，获取平衡态下模拟区域竖直方向上液膜、钠蒸气的密度分布，并与手册中对应温度下液态钠与饱和钠蒸气的密度参考值[17]进行了比较(该手册汇总了液态钠和钠蒸气的密度、饱和压力、焓差、比容等热力学性质)，除蒸气区个别数据误差在15%～19%外，其余数据误差均在10%以内。因此，势函数选取具备有效性。

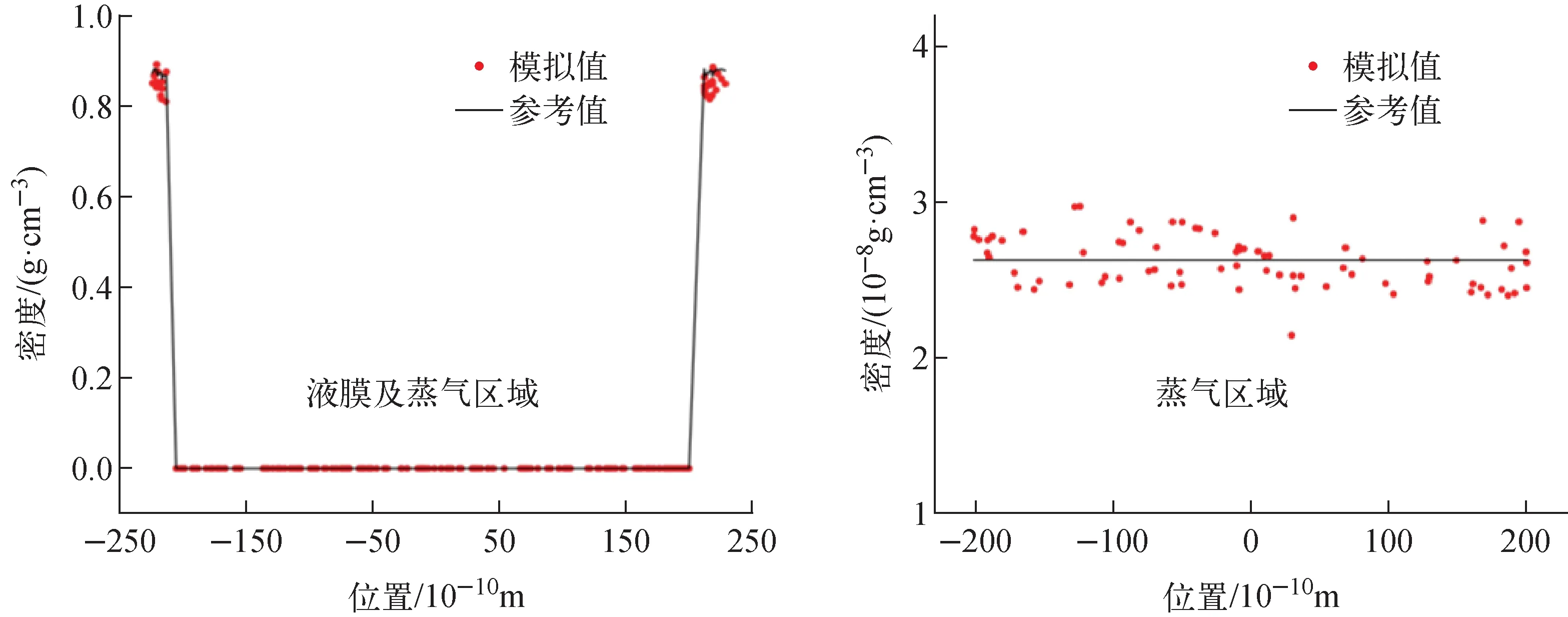
图6 竖直方向模拟所得密度与参考值的对比Fig.6 Comparison of density between simulated values and reference values in vertical direction

4 结果与讨论

4.1 钠工质平衡态蒸发过程

平衡态蒸发，即液膜、蒸气、热源壁面、冷源壁面的整体温度均在600 K左右，无明显温度梯度，气液交界的净热质输运接近于0。

对于Liang和Yu的统计方法，分别通过变更统计时间来改变穿入虚拟面气相原子数和通过改变虚拟空间与气液交界的距离进行多次统计，结果列于表2、3。Liang方法中，穿入虚拟面原子数由2 000增至10 577，质量调节系数变化很小，标准差0.024。Yu方法中，虚拟空间与气液交界距离发生改变，空间内所含原子总数变化不大(213～300)情况下，质量调节系数波动较大，标准差0.116 5，且会随着距离的减小而增大。同时，Yu方法所求值也远大于Liang方法所求值。

表2 不同统计时间下Liang方法所求质量调节系数Table 2 Mass accommodation coefficient obtained from Liang’s method in different statistic time

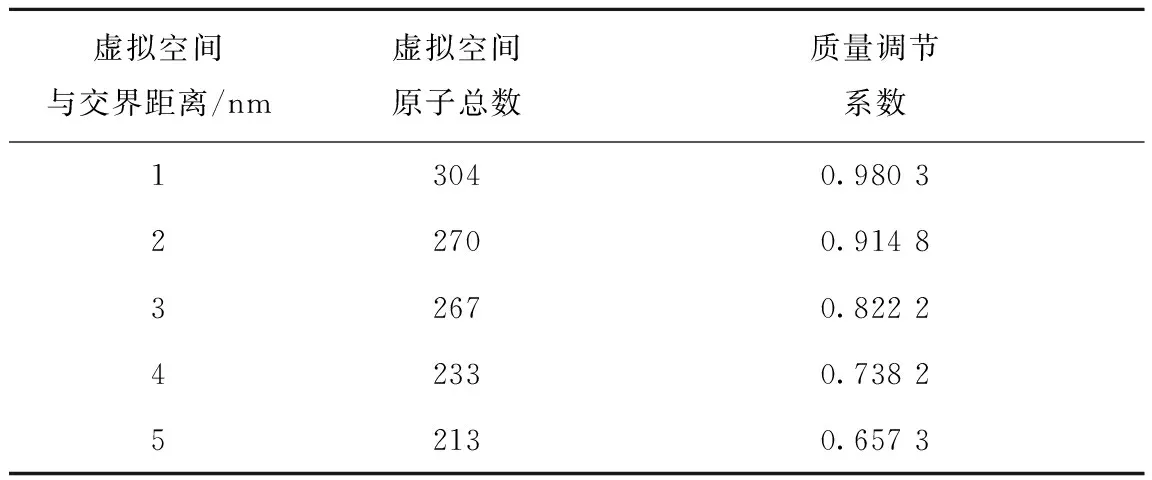
表3 不同虚拟空间与交界距离下Yu方法所求质量调节系数Table 3 Mass accommodation coefficient obtained from Yu’s method in different distances between virtual space and interface

平衡态时下部液膜及邻近蒸气区的温度、势能分布如图7所示，此时液相原子间相互吸引作用比较强烈(-0.3～-0.7 eV)，且作用范围大，即使在气液交界，这种吸引作用也依旧存在(-0.2 eV)。液膜主体区域温度在580～610 K范围内，能量差异小，这些区域内的原子不易摆脱周围原子的束缚成为气相原子。邻近蒸气区，除局部气相原子温度较高(700～800 K)，能量较大外，其余大部分原子温度在520～630 K范围内，在运动至交界后，所剩能量也不足以摆脱交界及液膜区的吸引，更易被冷凝。Yu方法中，当虚拟空间与交界的距离减小，虚拟空间内的气相原子所受吸引作用增强，更易在到达交界后成为冷凝原子，使统计值增大。而且，Yu方法忽视了虚拟空间外部区域的气相原子的运动，使统计样本缺乏整体性。

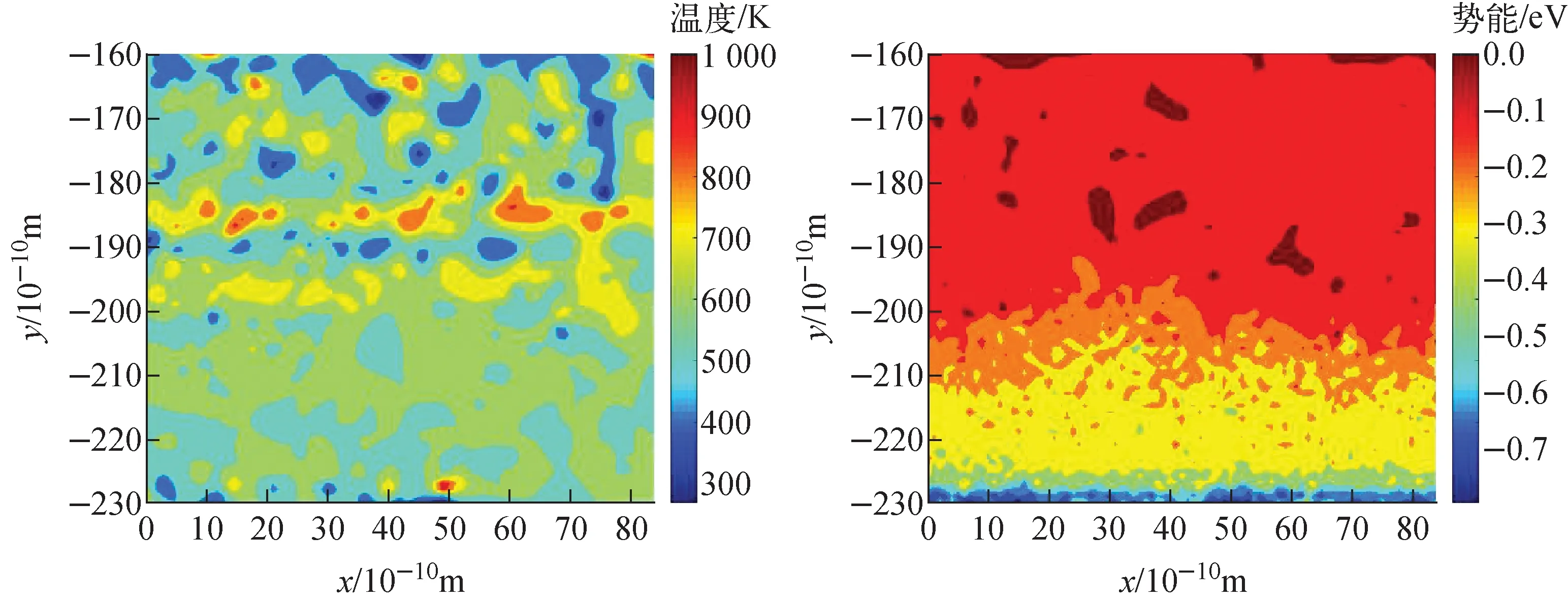
图7 平衡态时下部液膜及邻近蒸气区域温度、势能分布Fig.7 Distributions of temperature and potential in bottom liquid film and near vapor zone under equilibrium condition

Liang方法中，延长统计时间，穿入虚拟面气相原子总数增多，且最终远多于非平衡起始阶段气相原子数目，根据输出的钠原子运动轨迹信息，一方面是由于统计时间延长，模拟区域另一侧的气相原子也会穿入虚拟面，另一方面存在穿出虚拟面后，一段时间后又穿入虚拟面并发生前节所述3种行为的气相原子，这些原子会随着统计时间的延长而被计入样本总体。统计时间变更，所得数据有所变化，但差距在7%以内。综合来看，Liang方法更适用，且50 ps统计时间适中，兼顾前面所述两方面的影响。因此，质量调节系数定为0.388 7。

4.2 钠工质非平衡态蒸发过程

在平衡态模拟基础上，热源壁面设为720 K，冷源壁面设为520 K，使平衡态钠蒸发过程进入非平衡过程。壁面变温使液膜、壁面、蒸气区域之间出现了明显的温度梯度，气液交界的热质输运平衡被打破。此时液膜变化如图8、9所示。壁面升温，下部液膜蒸发加剧，厚度为2.5 nm的液膜开始减薄，11 ns后在0.1～0.52 nm范围内波动。同时，气相原子在上部冷凝，上部液膜厚度由2.87 nm增至6.25 nm。如图10所示，0～3 ns，蒸气区域原子数由3 900增至4 225，随后减少，末期数目为1 429。

图8 非平衡态下液膜演变Fig.8 Change of liquid film under non-equilibrium condition

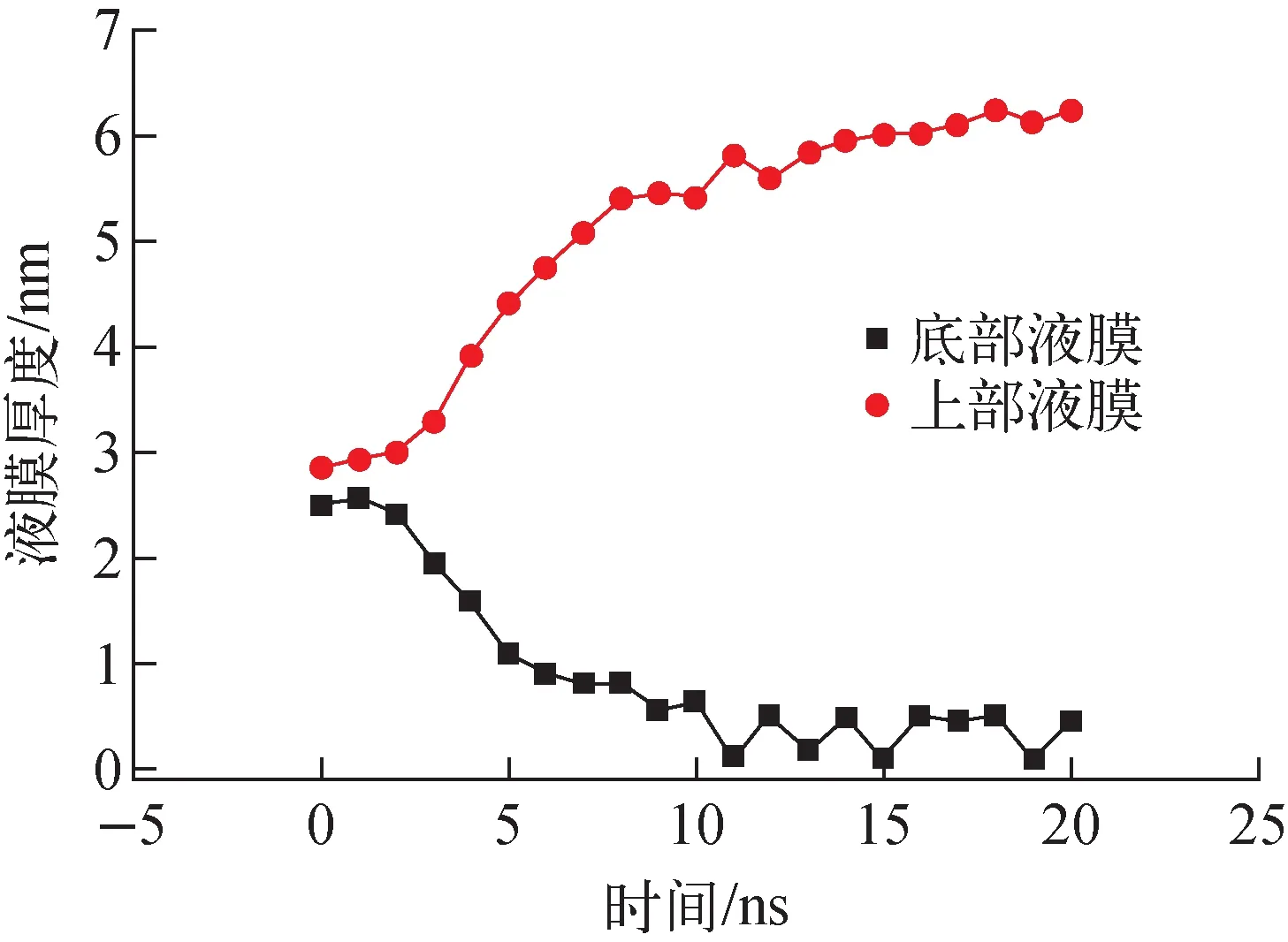
图9 非平衡态下液膜厚度变化Fig.9 Change of liquid film thickness under non-equilibrium condition

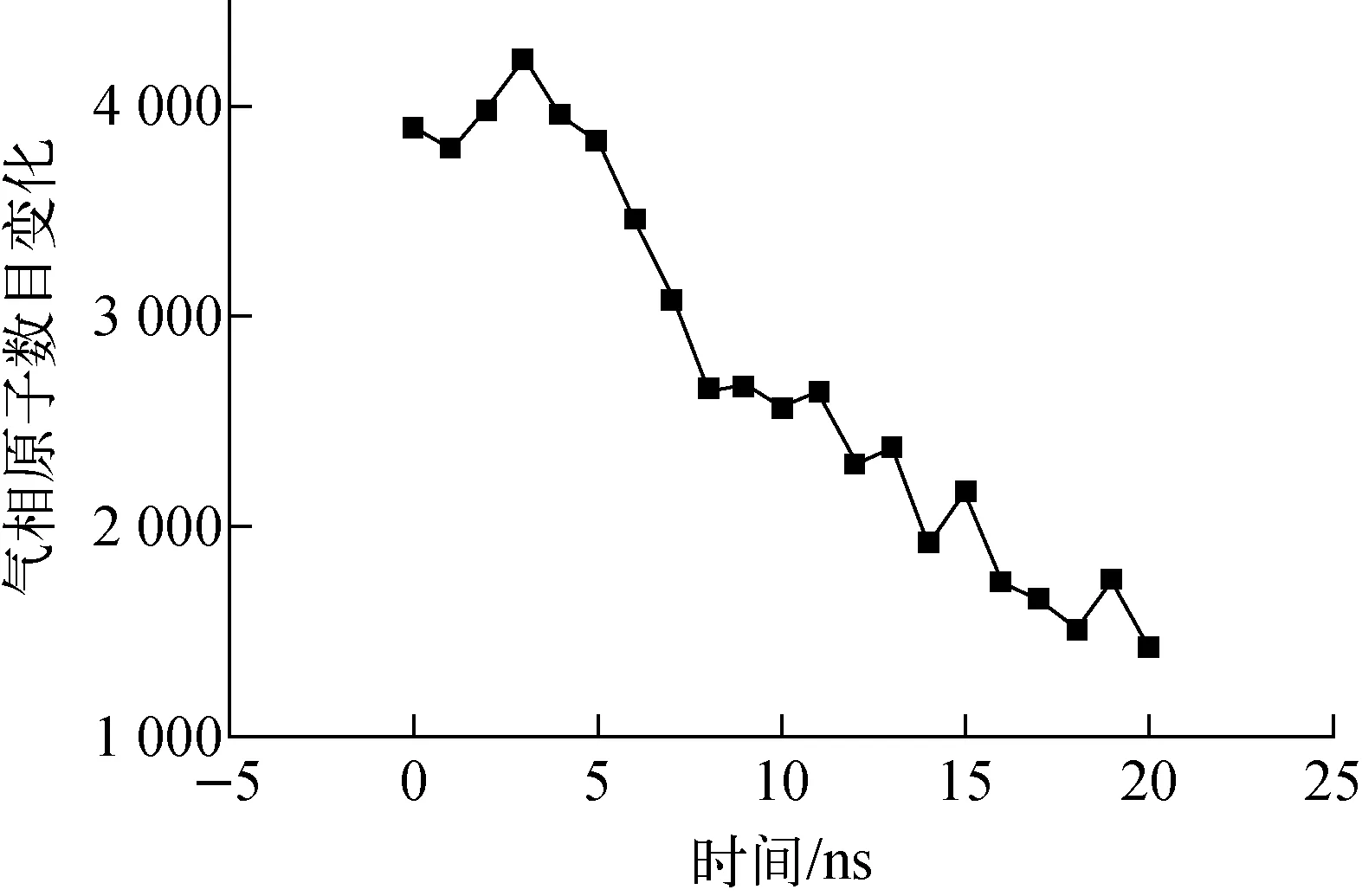
图10 非平衡态下气相原子数目Fig.10 Number of gas atomunder non-equilibrium condition

净蒸发通量如图11所示。0～5 ns，下部交界净蒸发通量在0.002～0.003 kg/(m2·s)范围内，随后增大，15 ns达到0.069 2 kg/(m2·s)后，出现波动，范围在0.03～0.07 kg/(m2·s)内。在上部交界，0～4 ns，净蒸发通量在0.001 9～0.002 6 kg/(m2·s)范围，之后下降，9～20 ns，净蒸发通量在10-4量级，上部交界传质接近平衡。

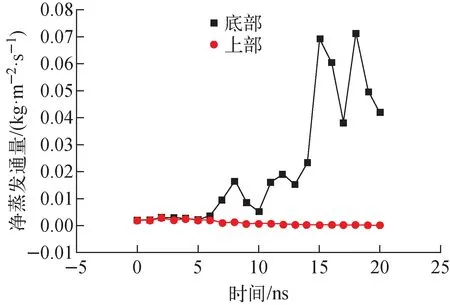
图11 交界面净蒸发通量Fig.11 Net evaporation mass flux at liquid-gas interface

交界换热系数如图12所示。0时刻，壁面变温，造成扰动，使交界换热系数为非零值(下部交界换热系数更明显)。下部交界，0～1 ns交界换热系数由10 kW/(m2·K)降至0.399 kW/(m2·K)，随后增大，3 ns达到14 kW/(m2·K)后开始下降，11 ns后在2.2～3.9 kW/(m2·K)范围内波动。上部交界，4 ns交界换热系数增至3 kW/(m2·K)后，开始下降，11 ns为0.028 kW/(m2·K)，最终降至0.003 5 kW/(m2·K)。

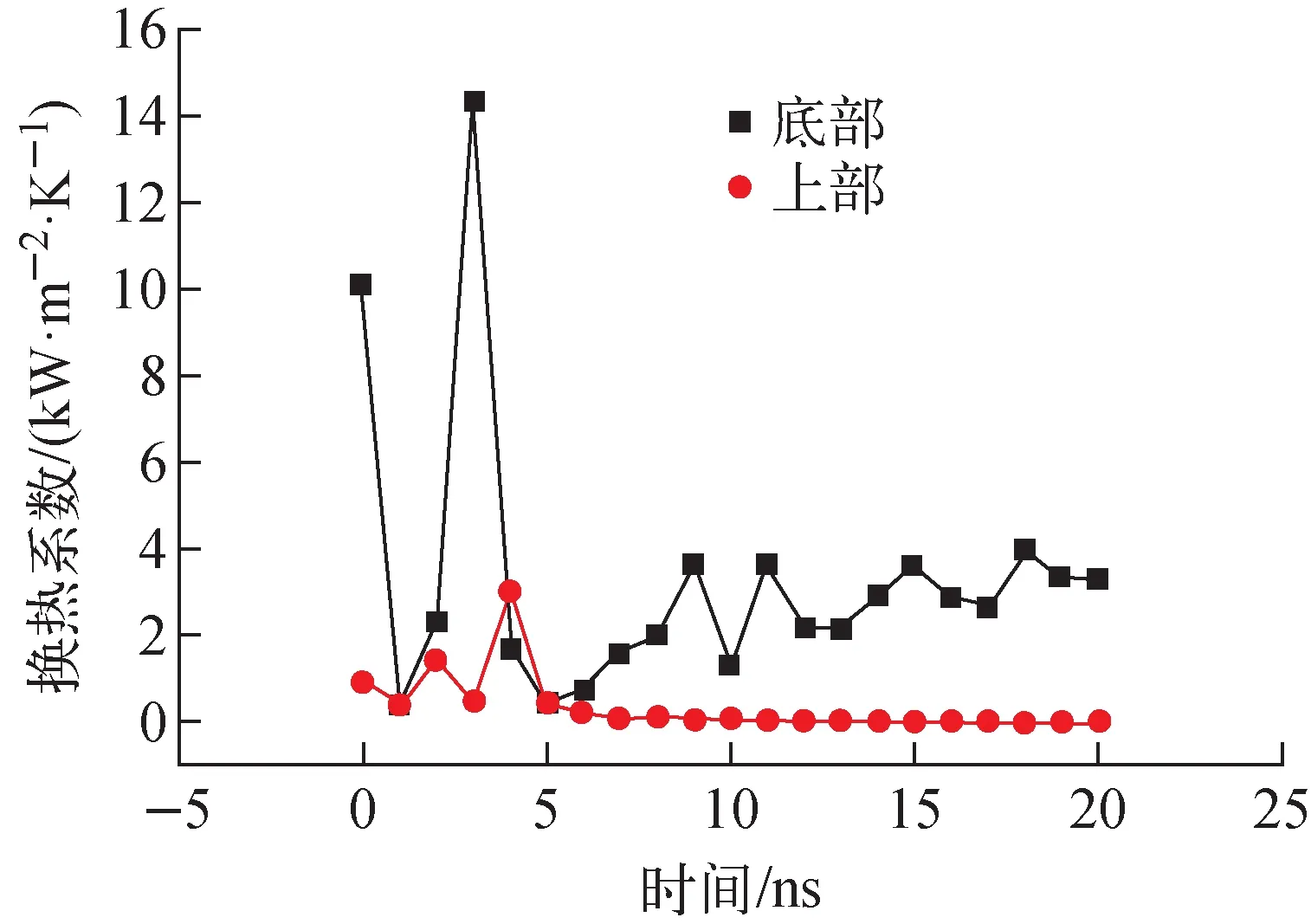
图12 交界面换热系数Fig.12 Heat transfer coefficient at liquid-gas interface

对于下部交界，结合图9、11中液膜变化、净蒸发通量来看，0～1 ns时，壁面升温初始，传递热量不多，只有少量液相原子得到这些热量，并在液膜内的运动中将其快速耗尽，液膜升温还不明显，交界处传热较为微弱。从1 ns开始，壁面进一步升温，传递热量增多，液膜开始变化，此时液膜和蒸气区之间出现明显热量差异，交界传热量开始加大，所以下部交界换热系数在0～3 ns出现了先降后升的趋势。0～3 ns，交界处的传热也使气相原子的温度上升，液膜和蒸气区之间的热量差距开始缩小，使此时交界换热系数开始下降。

对于上部交界，结合0～5 ns净蒸发通量变化，可看出该阶段气相原子到达上部交界后，所剩能量与上部液膜内原子相比，差异不大，传热量较少，使得上部交界换热系数变化幅度不大。9～20 ns时，上部交界的传质接近平衡，表明冷凝释热与蒸发吸热也趋近于平衡。因此9 ns后，交界换热系数进一步降至很低量级。

非平衡态下5、10、15、20 ns时下部液膜及邻近蒸气区域温度、势能分布分别如图13、14所示。可看出，下部液膜减薄，液膜及交界处的原子间吸引作用却依旧强烈(-0.4～-0.7 eV)。同时，在液膜变薄，液相原子较少的情况下，壁面对钠原子(特别是气相原子)的作用开始凸显，并逐渐增强。但在另一方面，非平衡态进行时，下部壁面升温，热量的传递也使钠原子能量大幅增加，挣脱束缚能力增强。三者的综合作用，使11 ns后下部交界换热系数、下部液膜厚度及15 ns后下部交界净蒸发通量的反复波动。

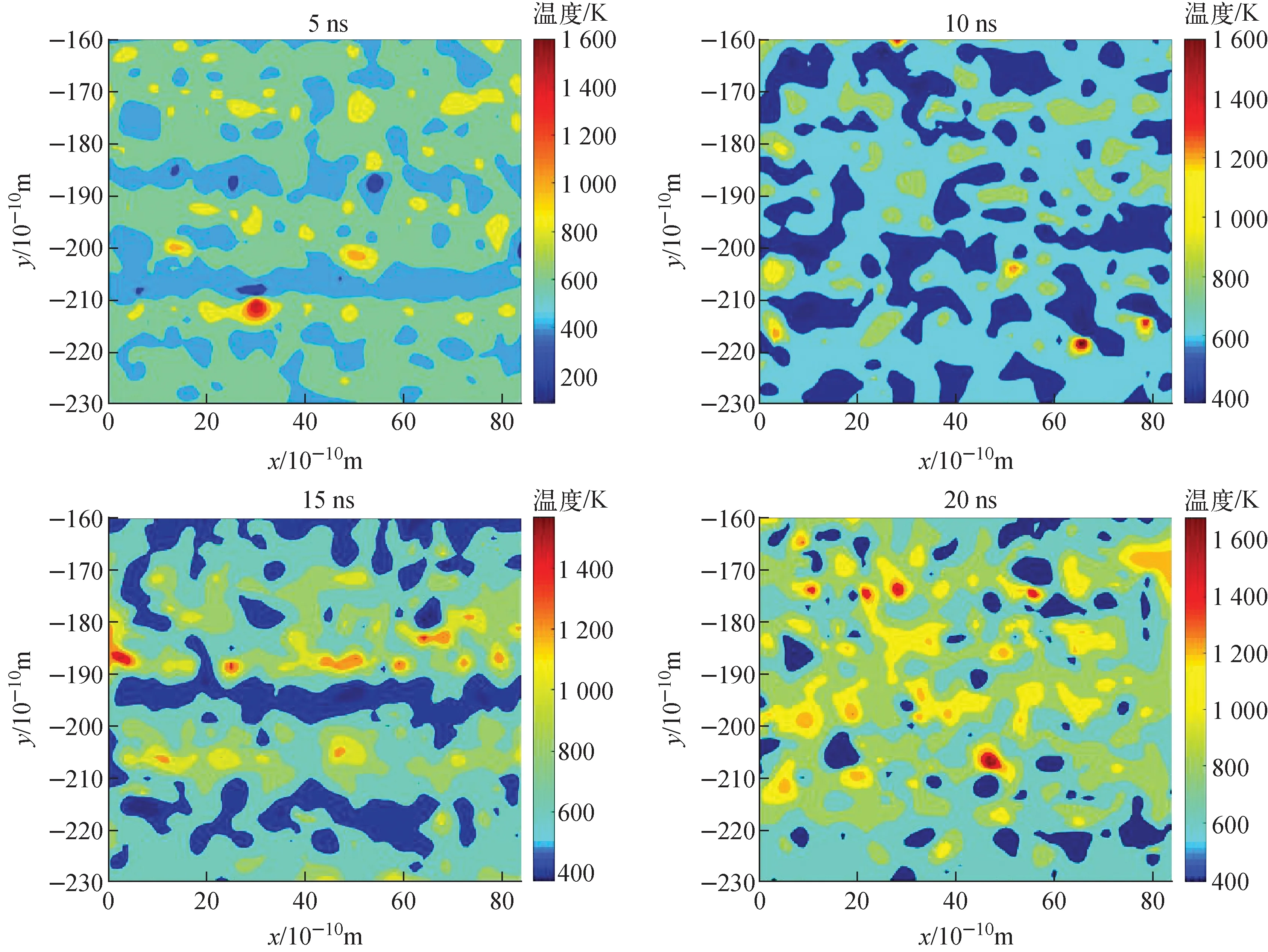
图13 非平衡态下5、10、15、20 ns时下部液膜及邻近蒸气区域温度分布Fig.13 Temperature distributions of bottom liquid film and near vapor zone at 5, 10, 15, and 20 ns under non-equilibrium condition

热管数值模拟中多采取热阻网络法[18]进行传热分析。从液膜厚度和交界换热系数的变化来看，启动阶段，当吸液芯孔洞中液膜厚度达到4～5 nm时，需考虑气液交界处的热阻。因此，可进行一些表面改性工作，制备润湿性更好、毛细力更强的吸液芯材料，用于热管制造中以降低液膜厚度。

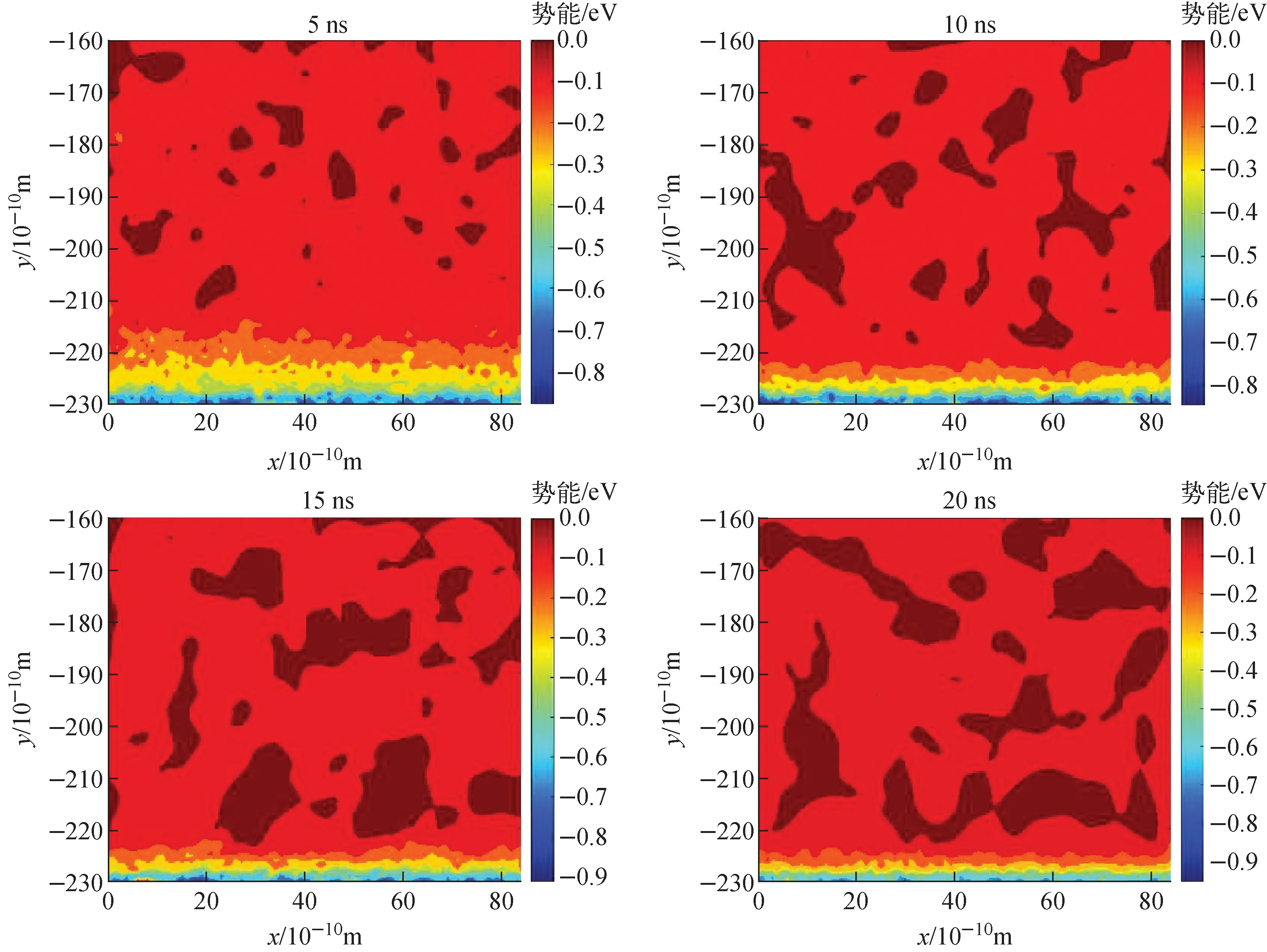
图14 非平衡态下5、10、15、20 ns时下部液膜及邻近蒸气区域势能分布Fig.14 Potential distributions of bottom liquid film and near vapor zone at 5, 10, 15, and 20 ns under non-equilibrium condition

5 结论

本文首次从分子动力学角度出发，对高温热管的启动阶段钠工质蒸发冷凝过程进行机理性研究。用LAMMPS软件模拟了高温钠工质600 K时平衡态与非平衡态蒸发过程，获得了钠工质启动过程中质量调节系数、液膜厚度、净蒸发通量与换热系数等关键参数，为进一步明确碱金属工质的蒸发与冷凝机理奠定了基础，具体结论如下。

1) 600 K时Liang方法更适用于统计质量调节系数，所得值为0.388 7，与高温热管模拟时常假设的α=1存在较大差距，可为钠热管工况数值模拟提供参考。

2) 非平衡态蒸发进行9～11 ns后，下部液膜内原子间作用依旧强烈，壁面对气液两相原子的吸引也逐步增强，同时壁面升温使原子能量增大，三者的综合作用造成底部液膜厚度、气液交界净蒸发通量、换热系数的波动。而此时上部交界传质接近平衡，热量传递不再明显。

3) 液膜厚度、气液交界换热系数的变化表明，钠热管启动阶段的数值模拟中，交界处传热模型需结合吸液芯孔洞液膜厚度变化进行选择。液膜厚度5 nm以上，该处热阻不可忽视，因此可考虑采用润湿性更强、毛细力更大的吸液芯结构以降低液膜厚度。