基于气泡动力学的过冷流动沸腾边界层模型研究

何 雯，赵陈儒，薄涵亮

(清华大学 核能与新能源技术研究院，北京 100084)

在压水堆和一体化小型水堆的热工设计中，不但允许堆芯冷却剂发生过冷沸腾，还允许在少量冷却剂通道中发生饱和沸腾，其目的是在一定的系统压力下，提高压水堆堆芯出口处的冷却剂温度，以及一体化小型水堆的自然循环能力，从而改善整个核电站的热效率。因此，研究过冷流动沸腾中的流动和传热特性对反应堆的安全运行和经济性都具有重要意义[1]。然而，流动沸腾过程非常复杂，涉及到质量、动量和能量的交换，且伴随着大量气泡的产生、生长、脱离、运动和冷凝，以往关于流动沸腾过程的研究主要集中于宏观实验、理论研究和数值模拟。随着气泡动力学研究的发展，揭示流动沸腾微观机理成为可能，而气泡动力学研究成果也为过冷流动沸腾的机理揭示和理论模型发展奠定了宝贵的基础。

工程上通常采用两流体模型来描述反应堆中的沸腾两相流动，能较直观地获得两相的宏观特性。李小畅[2]基于两流体模型对压水堆棒束子通道的两相流动进行了模拟。张小英等[3]采用两流体模型针对核反应堆蒸汽发生器二次侧的单元通道过冷段进行了数值模拟，获得了通道内空泡份额、温度、速度等参数。此外由于两流体模型中封闭子模型较多，如壁面热流密度分割模型、湍流模型、气液之间界面力模型等，很多研究者对其敏感性进行了分析。Cheung等[4]通过改变壁面热流密度模型中的气泡脱离直径、脱离频率和活化核心密度模型，耦合两流体模型对过冷流动沸腾进行了数值模拟。Yeoh等[5]采用群体平衡方法(PBM)根据气泡在主流流场的运动行为建立了气泡密度平衡方程，耦合两流体模型，对实际主流中存在多粒径的气液两相流进行了数值模拟。Mali等[6]对不同相界面模型和湍流模型的准确度进行了评估，然后基于两流体模型对过冷流动沸腾进行了模拟。然而，尽管数值模拟应用广泛，但为了描述两相界面处的质量、能量和动量交换，数值模拟通常需要较多的相界面方程。当应用到大规模工程计算时，这些方程将增加模拟所需的计算量，在计算过程中也容易导致发散。

基于实验得到的经验关系式是预测过冷流动沸腾的另一种方法。如，Cioncolini等[7]基于2 673个实验数据提出一种空泡份额的预测方法；Cai等[8]则基于1 118个垂直圆管的实验数据对现有关系式进行评价，同样提出一种预测空泡份额的经验关系式。然而，这些关系式受限于所采用的实验数据，适用范围有限。因此，基于理论分析获得的机理模型是预测沸腾过程的一种更重要的方法。Levy[9]基于质量含气率和热平衡值的关系，提出一种预测空泡份额的方法；Zeitoun[10]认为当壁面气泡受到的蒸发作用和冷凝作用被打破时，气泡脱离壁面进入主流，提出了一种预测净蒸气产生点(OSV点)的理论模型；Okawa[11]同样提出一种预测OSV点的方法，认为该点的出现与泡状流向弹状流的转变有关。然而，尽管理论模型较经验关系式具有更广的适用范围，但与经验关系式相同，对过冷沸腾的预测都是一维流动，即仅考虑流场在轴向上的质量、能量和动量交换，而忽略了径向上的气泡行为和传热传质，进而降低了这些关系式或模型的精准性。因此，有必要提出一种预测过冷流动沸腾的新方法，该方法与一维模型相比能获得更多的两相参数，又能较数值模型更稳定、精确、计算量更小。

沸腾过程中的传热传质与气泡行为息息相关，对沸腾过程的预测离不开对气泡行为的准确描述。杜静宇[12]基于气泡边界层的概念，将流场划分为主流和边界层两个区域，基于气泡动力学子模型对气泡边界层进行建模，重新建立了沸腾传热机理模型，用于沸腾曲线和临界热流密度的预测，并给出了气泡从边界层进入主流时的速度和尺寸分布，通过数值模拟将该边界条件与主流流体模型进行了初步单向耦合。周毓佳[13]则主要对主流区域内的气泡动力学特性进行建模和分析，建立了泡状流下单气泡在流场中的受力和运动模型，并基于欧拉-拉格朗日框架，将气泡边界层模型单向耦合到主流流场的数值模拟中，对过冷流动沸腾下主流区域的多气泡运动特性进行了分析。何雯等[14-16]基于现有实验数据，对边界层区域内气泡动力学参数的影响因素和概率分布进行了分析，包括脱离直径、活化核心密度和脱离频率，对这些参数的现有经验关系式进行评价，并针对脱离直径和脱离频率提出了新的预测模型。关舜然[17]基于非均匀多尺寸模型，在欧拉-欧拉框架下对绝热两相流动工况中的气泡聚并和破碎进行了研究，在欧拉-拉格朗日框架下，基于气泡动力学微观描述和气泡边界层及气泡运动模型，对过冷沸腾中主流气泡的聚并、破碎对气泡运动和尺寸分布的影响进行分析，建立了综合考虑气泡聚并、破碎、冷凝的离散气泡运动模型，并运用于数值模拟中。可见，目前对于气泡在过冷流动沸腾中的行为已有较成熟的认识，而将流场划分为主流和边界层两个区域的概念不仅能简化流场的计算，还能获得更多径向上的流场信息。然而，两个流场间的传热传质过程目前仅能通过数值模拟进行单向耦合，两个区域内流场的传热传质和气泡行为还有待进一步研究。

因此，本文基于气泡动力学和气泡边界层模型，提出一种预测过冷流动沸腾的新的理论模型，在径向上将流场划分为多个区域，采用气液两相流动的分相模型描述不同区域内的气泡行为和流动传热传质，利用一套准二维质量、能量和动量方程对流场进行数学建模，进而获得不同区域内的流场信息；基于所获得的边界层流场信息，可确定ONB点和OSV点。

1 理论分析

1.1 物理模型

过冷流动沸腾起始于单相过冷液体，沿轴向方向当壁温超过液体的饱和温度时，第1个气泡开始在壁面核化，此时，流场到达沸腾起始点(ONB点)，该点为流场从单相转变为两相的转折点。ONB点之后，流场进入高过冷沸腾段，此时不断有气泡在壁面核化并逐渐长大，但由于过冷度仍较高，这些气泡通常仅附着在壁面，既不滑移也不浮升，空泡份额也较低[8]。随着流场的逐渐升温，当气泡长到足够大时，受曳力的影响将离开核化点，部分沿着壁面滑移，部分直接离开壁面进入主流[18]。通常将气泡离开核化点的位置定义为OSV点，该点之后流场进入低过冷沸腾段，此时主流内开始出现气泡，空泡份额会出现明显上升，直至流场温度达到饱和状态，即Tsat点。由此可见，过冷流动沸腾可划分为高过冷沸腾段和低过冷沸腾段，不同阶段流场情况和气泡行为存在较大的区别，需要进行单独分析。

基于气泡边界层的思想，本文仍将流场划分为主流和边界层两个区域，采用气泡脱离直径作为边界层的厚度[12]。气泡达到该尺寸后开始离开核化点，部分进入主流，而沿着壁面滑移的气泡的尺寸和形状基本不变[18]，因此会形成一个附着在壁面的气泡层。气泡边界层与常采用的温度边界层和速度边界不同，前者定义为流体与壁面的温度差达到主流流体与壁面的温度差的99%处到壁面的距离，主要反映边界层内的对流换热效果，后者定义为沿壁面切向的流动速度达到自由来流速度的99%处到壁面的距离，主要反映边界层内动量和质量的损失情况。三者的相对大小受工况的影响较大，需要后续进行深入研究。本文以恒热流下垂直圆管内过冷流动沸腾为例进行分析，各阶段两个区域内的气泡行为如图1所示。

图1 恒热流下垂直圆管内过冷流动沸腾示意图Fig.1 Schematic diagram of subcooled flow boiling in vertical heated tube under constant heat flux

准确预测ONB点对反应堆运行安全至关重要，因为空泡份额的变化会对反应性造成较大的波动[8]。通常情况下，当壁面附近的流场能满足气泡生长所需要的能量时，ONB点出现，因此，确定ONB点相当于是确定满足气泡生长的流场环境。基于能量平衡，气泡的生长通常受3部分能量的影响，即过热液层的蒸发、微液膜的蒸发和过冷流体的冷凝。Raj等[19]发现，当过冷沸腾气泡在壁面稳定存在时，过热液层通常小于气泡直径，即气泡底端为过热流体，而顶端仍为过冷流体，此时气泡受到的蒸发作用和冷凝作用平衡。考虑到流动沸腾流场非常复杂，尤其是近壁面，且温度分布很难准确确定，因此，本模型假定在ONB点和OSV点处，边界层内温度线性分布，当气泡稳定附着在壁面时，其中心位置温度等于饱和温度。对于ONB点气泡对应的尺寸，受装置测量精度的限制，通常能测到的最小气泡尺寸为0.01 mm，因此假定ONB点处出现的第1个气泡的尺寸为0.01 mm，中心位置温度为TONB，而OSV点对应的气泡尺寸即为脱离直径(Dd)。若气泡边界层的平均温度为Tb，则可通过ONB点气泡中心温度TONB和壁面温度Tw及气泡边界层的平均温度Tb来确定ONB点，具体公式如下：

(1)

这样，对于高过冷沸腾段，边界层平均温度低于饱和温度，处于过冷状态；对于OSV点，边界层平均温度等于饱和温度，处于饱和状态；对于低过冷沸腾段，边界层平均温度大于饱和温度，处于过热状态；而在Tsat点，过热度达到最大值。显然，随着气泡边界层平均温度的逐渐上升，边界层内空泡份额逐渐上升。

1.2 基本假设

为简化计算，假定流场为稳态流场且忽略截面径向压力波动和轴向压力变化对物性的影响。此外，根据前文的分析，对ONB点和OSV点重新定义，认为两个点的位置需要同时满足气泡尺寸分别达到0.01 mm和脱离直径，且气泡周围流场的平均温度等于饱和温度两个条件。若认为过冷流动沸腾段边界层内平均温度和空泡份额均呈线性增加，则确定ONB点和OSV点的空泡份额以及饱和点对应的平均温度和空泡份额就非常重要。对于ONB点，由于气泡数量少且尺寸小，可认为空泡份额为0。而对于OSV点，本文假定边界层空泡份额等于0.3，原因在于Okawa[11]认为OSV点后空泡份额的快速上升与气泡的聚并有关，基于现有的流型转变机理，认为此时边界层内气泡呈四面体晶格排列，对应的空泡份额为0.3。而对于饱和点，目前尚未见有研究对该点气泡在壁面空间排列的分析，在课题组目前的研究中，通过分析不同边界层空泡份额对模型准确性的影响发现，边界层空泡份额取0.5时准确度最高，此时气泡在壁面近似呈均匀的紧密排列，因此本文取该值作为饱和点对应的值。此外，由于此时边界层内气泡沿壁面滑动，对流场进行扰动，此时边界层内温度分布不能再假定为线性分布，而应取对数分布，经过敏感性分析，此时取边界层过热度等于壁面过热度的1/3，准确度更高，具体研究成果将在后续文章中详述。

综上，该模型所有的基本假设如下：1) 流场为稳态流场；2) 截面径向压力波动和轴向压力变化对物性的影响忽略不计；3) 气泡边界层的厚度等于气泡脱离直径，气泡仅在边界层内产生和生长；4) ONB点的气泡尺寸等于0.01 mm，且周围流场的平均温度等于饱和温度；5) OSV点的气泡尺寸等于脱离直径，且周围流场的平均温度等于饱和温度；6) 过冷沸腾边界层内的空泡份额呈线性上升，ONB点空泡份额为0，OSV点空泡份额为0.3，饱和点空泡份额为0.5；7) 过冷流动沸腾边界层内的平均温度呈线性上升，ONB点温度过冷，OSV点温度等于饱和温度，饱和点温度等于壁面过热度的1/3。

2 数学描述

2.1 基本方程

由于低过冷沸腾段的气泡行为更复杂，因此以该段为例展示数学模型的建立过程，单相段和高过冷沸腾段的数学模型可由该模型简化得到。与主流相比，边界层内气液两相的流速较小，两者之间的速度差可忽略，再加上边界层内两相的温度一致，因此该区域可基于均相流模型描述。相反，由于主流内气液两相同时存在温度差和速度差，因此该区域需要基于分相流模型描述，被二次划分为主流液体区域和主流气体区域，具体如图2所示。各区域之间由于气泡或液体的运动会存在质量、能量和动量的交换。

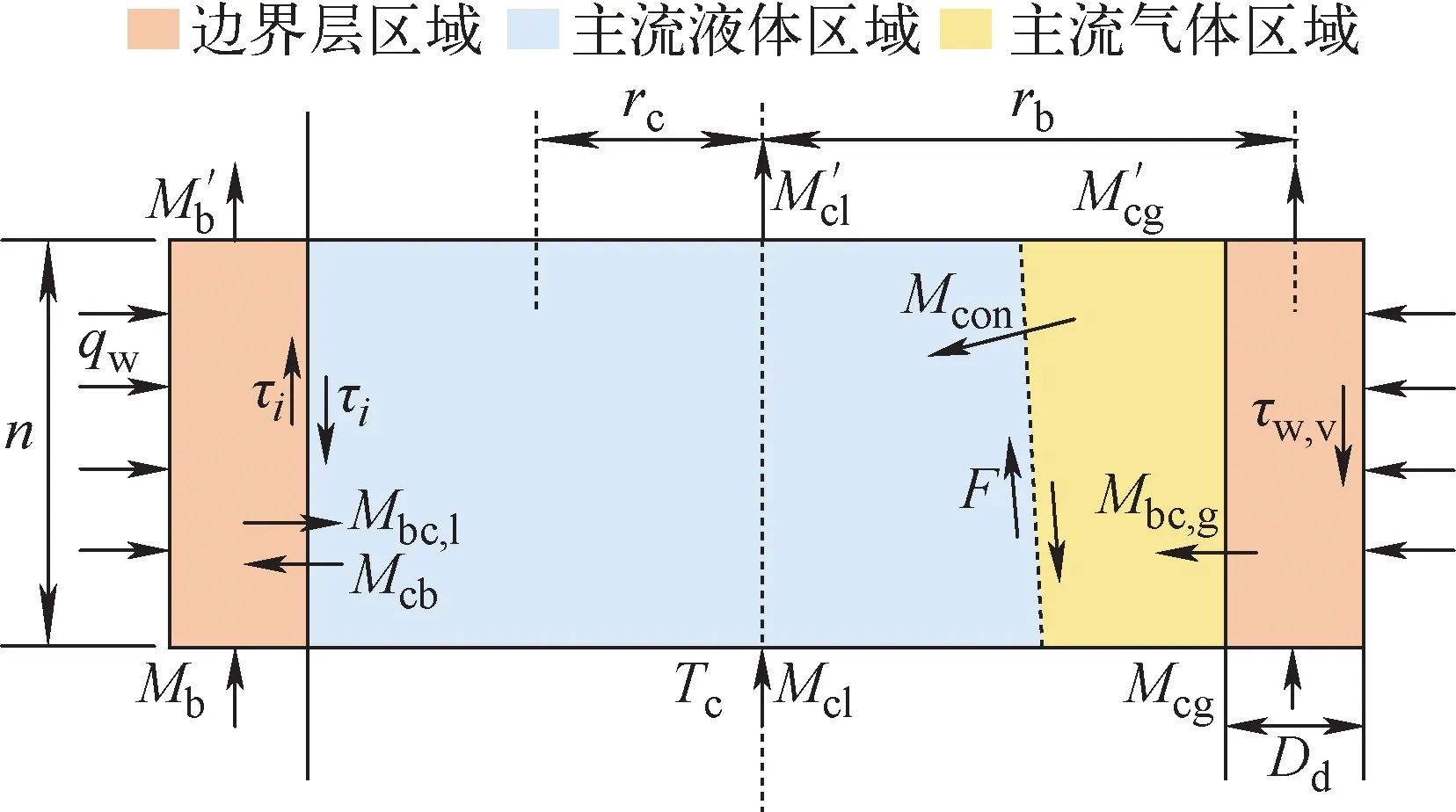
图2 低过冷流动沸腾段数学模型Fig.2 Mathematical model for slightly subcooled flow boiling

对于质量交换，由于气泡在壁面不断产生并携带部分液体进入主流，因此从边界层进入主流的为气液两相，相反，由于气泡进入主流后随流体以更高的流速运动，因此仅考虑液相从主流返回边界层进行下一轮蒸发。基于此，对于边界层区域、主流液体区域和主流气体区域，质量守恒方程分别如下：

M′>b-Mb=Mcb-Mbc

(2)

M′>cl-Mcl=Mbc(1-xb)-Mcb+Mcon

(3)

M′>cg-Mcg=Mbcxb-Mcon

(4)

其中：Mb、Mcl和Mcg分别为边界层、主流液体区域和主流气体区域的质量流量；Mcb和Mbc分别为主流进入边界层的质量流量和边界层进入主流的质量流量；Mcon为冷凝质量流量。

对于能量交换，壁面的热量首先传递给边界层，用于气泡的蒸发，而后再通过与主流的质量交换将能量传递到主流，3个区域的能量方程如下：

qwξwn+McbHcl-MbcHb-Qc=

M′>bHb-MbHb

(5)

Mbc(1-xb)Hbl-McbHcl+HcgMcon+Qc=

M′>clH′>cl-MclHcl

(6)

MbcxbHbg-HcgMcon=M′>cgHcg-McgHcg

(7)

其中：qw为热流密度；ξw为管道周长；xb为边界层区域质量含气率；Hcl和Hbl分别为主流和边界层液体的焓；Hcg和Hbg分别为主流和边界层气体的焓(Hcg=Hbg)；Hb为边界层混合物的焓；Qc为边界层和主流液体之间的导热量。由于两个区域存在温差，以圆管为例，有：

(8)

-Ab(p′-p)+τiζin-ρbgAbn-τw,vζwn+

McbUcl-MbcUb=M′>bU′>b-MbUb

(9)

-Acl(p′-p)-τiζin+F-ρclgAcln+

Mbc(1-xb)Ub+MconUcg-McbUcl=

M′>clU′>cl-MclUcl

(10)

-Acg(p′-p)-F-ρcggAcgn+MbcxbUb-

MconUcg=M′>cgU′>cg-McgUcg

(11)

其中：p为系统压力；ζi为主流与边界层交界面的周长；τi、τw,v分别为主流液体与边界层之间、边界层与壁面之间的应力；F为主流气液两相之间的曳力。

2.2 方程求解

对于低过冷沸腾段，未知数有9个，分别为系统压力(p)、主流空泡份额(αc)、3个区域的流速(Ub、Ucl、Ucg)、主流液体温度(Tcl)、冷凝量(Mcon)以及主流和边界层的径向交换量(Mbc，Mcb)，其中冷凝量通过冷凝方程求得。而对于控制方程，由于Hcg=Hbg，因此方程(4)和(7)一致，即控制方程为8个，因此，在获得3个力的条件下利用Matlab可对应求解。然而，力的求解需要获得交界面处的速度梯度，τi和τw,v可通过壁面速度分布公式获得，而由于主流气体在不断增多且形状变化较大，F的确定非常困难。因此，求解时将主流气液两区域的动量方程合并，消去F，补充滑速比公式用于反映两区域的流速关系，具体求解步骤可参考He等[20]的研究。而对于单相段和高过冷沸腾段，由于主流不存在气体，该区域仍基于均相流，因此控制方程只有6个，未知数减少为7个，分别为主流和边界层区域的流速和温度、压力、径向交换量。因此，通过补充壁面速度分布公式可求解。

2.3 封闭方程

1) 气泡脱离直径

气泡脱离直径Dd直接影响气泡边界层的厚度，目前，利用无量纲数将脱离直径各影响因素综合考虑在内的经验关系式法被广泛采用。杜静宇[12]采用大量实验数据，对现有经验关系式进行评价，然后重新提出一套将力平衡结合在内的经验关系式。但何雯等[14]发现该关系式的准确性随着普朗克数的增大而减小，因此对该关系式进行了修正，得到的新关系式准确度更高、适用范围也更广。因此，本模型采用该关系式计算脱离直径，其数学形式如式(12)所示。该公式的适用范围为：水力直径1～42.4 mm，壁面过热度0.5～50.1 K，液体过冷度2～50.1 K，质量流量67～1 927 kg/(m2·s)，工质包括水、HFE-301和FC-87。

(12)

其中，σ、μl、cp,l、λl和ilg分别为表面张力、液体动力黏度、液体比定压热容、液体导热系数和汽化潜热。

2) 滑速比公式

滑速比(S)定义为气液两相流速之比。滑速比的测定非常困难，原因在于流动沸腾中相变不停发生，且气体形状不断发生变化，因此目前关于滑速比的研究及相应预测模型不多[21]。由于气液两相的流速差通常随着气体含量的增多而变大，因此认为滑速比受质量含气率x的影响较大，其表示单位时间内流过通道某一截面的两相流体总质量中气相所占的比例。基于此，本文提出新的预测模型(式(13))，具体过程将在后续文章中详述。

(13)

得到滑速比后，空泡份额和质量含气率可通过式(14)进行转换，对于边界层，S=1。

(14)

3) 主流和边界层平均流速

与管道尺寸相比，气泡边界层通常很薄，对于垂直管道内的流动沸腾，气泡脱离直径的最可几值为0.162 mm[12]。因此，可假定这个区域内的流体速度呈线性分布，此时边界层区域的平均流速(Ub)为两区域交界面处流速(Ul)的1/2[20]，即：

Ub=Ul/2

(15)

而交界面处的流速可采用适用于单相湍流的对数分布公式计算：

(16)

(17)

其中：Ac和A分别为主流区域和管道截面的面积；G为质量流速；f为摩擦系数，是雷诺数(Re)的函数。

(18)

一旦Ub确定，则主流液体区域的平均流速可由下式计算：

Ucl=(GA-UbρbAb)/(ρclAcl+SρcgAcg)

(19)

而主流气体区域的流速则通过滑速比公式得到。对于单相段和高过冷段，主流没有气体，则主流区域的平均流速为：

Uc=(GA-UbρbAb)/ρcAc

(20)

4) 冷凝公式

对于低过冷沸腾段，气泡进入主流后由于温差会被冷凝，冷凝换热量计算公式如下：

dQcon(z)=kcon(Tcg-Tcl)dz

(21)

其中：Tcg和Tcl分别为主流气液两相的温度；kcon为冷凝系数，受多个参数影响，如流速、水力直径、热流密度等，采用Rouhani关系式[22]计算，适用范围为1.9～23.8 MPa下的水，热流密度为18～1 200 kW/m2。

(22)

其中：Cs为加热周长；α(z)为不同轴向位置处的截面空泡份额。一旦冷凝换热量确定，冷凝的质量流量Mcon可通过下式确定：

(23)

5) 黏性力

不同区域间由于速度差会产生黏性力，该力与流体黏性和界面处速度梯度有关，其中边界层的速度梯度可通过壁面速度分布公式获得：

(24)

3 模型验证和应用

3.1 模型验证

空泡份额是流动沸腾中的一个重要两相参数，对换热量、压降和流动不稳定性等均有影响。因此，本文采用垂直圆管内截面平均空泡份额的实验数据对模型进行验证，工质为水，由于低过冷沸腾段空泡份额更明显且呈快速增长，因此主要对这一阶段的空泡份额进行对比。Cai等[8]曾对预测过冷流动沸腾的现有经验关系式进行了对比和评价，包括OSV点的确定、质量含气率的计算以及质量含气率与空泡份额的转换关系等，基于大量实验数据得到一套用于预测垂直圆管内过冷流动沸腾的经验关系式的组合，因此，该模型也作为本模型的对比之一。为定量反映模型的准确性，定义绝对误差(MAE)如下：

(25)

图3为模型与Ferrell[23]和Rouhani[24]实验数据的对比，其中横坐标为热平衡干度(xth=(h-hl,sat)/ilg)，也称为热平衡含气率。可发现，本模型能对大多数工况下的空泡份额进行准确预测，MAE分别为29.1%和17.7%。与Cai模型[8]相比，本模型与实验数据的增长趋势更相近，且准确度更高。原因在于，Cai模型假定OSV点处空泡份额为0，即忽略此时边界层包含的气泡数量，因此会造成模型在起始段与实验数据存在差异，此外，Cai模型采用经验关系式确定OSV点的具体位置，该关系式的误差同样会对模型的预测结果造成较大的影响。图4为模型预测与Mali等[6]实验中空泡份额和流体温度的准确性对比。图4显示，模型对流体温度预测的准确度高，MAE为0.3%，对空泡份额预测的准确性虽不如Cai模型，但仍与实验数据相差不大，MAE为15.8%。

图3 低过冷流动沸腾段空泡份额预测值与实验数据的对比Fig.3 Comparisons of predicted void fraction with experimental data in slightly subcooled flow boiling

图4 低过冷流动沸腾段空泡份额和液体温度预测值与实验数据的对比Fig.4 Comparisons of predicted void fraction and temperature with experimental data in slightly subcooled flow boiling

综上，通过与垂直圆管内空泡份额和流体温度实验数据的对比，可证明本模型在预测过冷流动沸腾中具有较高的准确性，空泡份额整体误差为22.3%。由于实验数据有限，本文验证的工况如下：压力为0.827～4.5 MPa的水、质量流速为520～1 440 kg/(m2·s)、热流密度为243～888 kW/m2、水力直径为6.1～15.4 mm。尽管验证范围有限，但本模型主要依靠机理分析，普适性很广，本模型的适用性主要受封闭方程中经验关系式的适用范围影响，但影响有限，因此可认为本模型有应用到更大工况范围的潜力。后续基于更多的实验数据可对这些经验关系式以及本模型的适用性进行进一步确定和评价。

3.2 模型应用

为展现模型在工程应用上的意义，本文以某一体化自然循环小型水堆燃料元件加热通道工质为例，将其应用到反应堆堆芯出口温度恰好等于饱和温度的一种微沸腾工况，预测其过冷流动沸腾的状态，其棒束结构如图5所示，水自下向上流动，流速为0.5 m/s，系统压力为6.5 MPa，对应流体的饱和温度为554 K，流体入口过冷度为35 K，热流密度为189 kW/m2，管道长度为2.1 m，由于流场对称，因此选择其中1/4栅格进行计算。图6为两相参数沿通道方向的变化，需要说明的是，对于该工况，在低过冷沸腾开始阶段，由冷凝公式计算得到的冷凝量大于边界层进入主流的气体含量，造成起始阶段主流空泡份额为负，而出现该现象的原因可能来自冷凝公式的误差。为避免该现象的出现，计算该工况时对冷凝公式乘以0.3进行修正，而在不同工况下的修正情况将在后续文章中进一步讨论。结果显示，整个过冷沸腾段的长度占总长度的52.6%，ONB点和OSV点的位置分别距离通道出口1 764 mm和1 300 mm，这两个点的确定对燃料元件通道内流场的分析，如不同运行工况的影响、反应性的影响、自然循环能力的增强等都非常重要，对反应堆微沸腾工况安全运行和经济性也具有重要意义。此外，3个区域的空泡份额、流速以及系统压力的变化也分别示于图6b～d。值得说明的是，边界层流速在OSV点前后出现明显变化，原因在于OSV点前模型采用壁面速度分布公式获得边界层流速，并假定此时边界层内速度呈线性分布，而OSV点后由于控制方程的增多，模型不再采用该公式和假设。

图5 燃料元件通道内的管束结构及流道Fig.5 Tube bundle structure and flow passage in fuel element channel

图6 燃料元件通道内过冷流动沸腾两相参数的变化Fig.6 Variations of two-phase flow parameter in subcooled flow boiling in fuel element channel

4 结论

本文基于气泡动力学理论提出了一套用于预测过冷流动沸腾的边界层模型，该模型在径向上将流场划分为多个区域，通过一组准二维质量、能量和动量方程，将不同区域内的气泡行为和区域间的传热传质考虑在内，其中主流区域主要基于分相流模型，边界层基于均相流模型。利用获得的边界层流场信息，本文提出了一种确定ONB点和OSV点的新方法，与垂直管道内的空泡份额和流体温度的实验数据进行了验证对比，绝对误差分别为22.3%和0.3%，并成功应用于某一体化自然循环小型水堆燃料元件通道流体的计算。

随着研究的进一步深入，本模型将考虑更多的气泡动力学过程，并将推广至饱和沸腾，获得更大范围流动沸腾的计算分析，可为压水堆和一体化小型水堆的热工设计和安全分析提供有效的计算分析工具。