压水堆堆芯pin-by-pin计算环境效应处理模型研究

张 斌，李云召，吴宏春

(1.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610041；2.西安交通大学 核科学与技术学院，陕西 西安 710049)

受限于计算条件和计算方法的水平，基于确定论或蒙特卡罗方法的压水堆三维全堆芯非均匀一步法计算在反应堆中子学计算中尚无法得到广泛应用。因此，近代反应堆中子学计算从中子输运方程的空间、能量、角度3个方面进行合理近似得到了具有较高精度的两步法计算方案。该计算方案因内存需求量小、计算效率高、计算精度满足商用压水堆设计计算需求等优点而被广泛应用。

20世纪70年代以后，得益于粗网节块法[1-2]的迅速发展，以组件均匀化方法[3-4]和粗网节块法为理论框架的两步法计算方案逐渐成为压水堆工程计算中普遍采用的燃料管理数值计算方法。两步法计算方案通常先以全反射边界条件下的各类型二维燃料组件为对象进行中子输运和组件均匀化计算，给出组件均匀化少群常数和形状因子；然后将堆芯划分成几千个粗网节块，基于少群常数库进行中子扩散方程的求解；最后通过节块内精细功率重构方法获得堆芯中子通量密度分布和棒功率分布。两步法计算方案误差引入的主要因素之一是组件均匀化少群常数计算中采用的全反射边界条件与该组件在堆芯中实际所处环境的差异。对于商用压水堆，因其普遍具有径向及轴向材料布置非均匀性不强、堆芯中子泄漏小等特点，以尺寸较大的组件作为均匀化区域、采用全反射边界条件进行栅格计算得到的组件均匀化常数精度较高，满足堆芯核设计计算精度要求。

随着科学研究的不断深入、计算条件和对核设计计算精度要求的不断提高，全堆芯pin-by-pin计算成为下一代堆芯数值计算方法的研究热点[5-6]。相比于组件均匀化两步法计算方案，pin-by-pin计算方案只对组件中各栅元进行均匀化计算，保留了组件内不同栅元的非均匀性。全堆芯pin-by-pin计算减少了堆芯计算过程中的近似与假设，能更加精细地考虑堆芯布置的非均匀性，直接求出精度更高的棒功率分布，有利于堆芯燃料管理计算和相应堆芯安全分析。

随着栅元均匀化技术的发展[7-8]，全反射边界条件成为栅元均匀化常数误差的主要来源之一。基于广义等效均匀化理论，在边界条件一致的情况下利用栅元均匀化截面、扩散系数和不连续因子能保证均匀化前后反应率及中子泄漏率守恒。然而，燃料组件在真实堆芯中所处的实际环境在两步法计算中是无法提前获知的，目前全堆芯pin-by-pin计算中，栅格计算依旧采用全反射边界条件。全堆芯pin-by-pin计算的均匀化区域大小与平均中子自由程相当，这使得栅元均匀化常数对环境更为敏感，尤其是处于组件外围的栅元。

为进一步提高全堆芯计算精度，国内外学者探讨了大量的嵌入式计算方法(on-the-fly)、Color-set均匀化方法等改进型均匀化方法在复杂堆芯计算中的可行性及其计算精度。嵌入式计算方法[9-11]的主要思想是在堆芯计算中迭代进行非均匀组件计算用以在线更新均匀化群常数，该方法的优点在于能有效考虑燃料组件在堆芯中的真实环境情况，可计算得到更精确的均匀化常数，但迭代进行非均匀组件计算将增加计算代价，降低计算效率。Color-set均匀化方法[12-13]可提前制作少群常数库，避免嵌入式计算中堆芯计算效率降低等问题。该方法以4个组件交界点为Color-set问题几何中心，围绕该点的4个1/4燃料组件构成Color-set问题。Color-set均匀化方法能很好地考虑各不同组件之间的射流效应及能谱干涉效应，极大提升了等效均匀化少群常数的计算精度。但Color-set计算在实际应用中需针对堆芯中所有燃料组件的组合堆芯实际运行时，堆芯内所有位置的组合都将不同，提前制表的复杂性大幅增加，且这种复杂性会随燃耗、堆芯瞬态、物理热工耦合效应的考虑变得更突出。近年来，基于参数化技术提升群常数精度的研究逐渐增多，普渡大学于2004年提出了基于神经网络算法拟合pin-by-pin少群常数的计算方法[14]，但其只在用来拟合的状态点上可恢复出精度较高的少群常数；2017年，韩国KAIST大学研究了基于神经网络算法拟合群常数的算法，此类方法在pin-by-pin均匀化常数中取得了很好的计算效果。然而受限于神经网络算法输入参量的选择，此方法只适用于两群等效均匀化常数拟合计算，适用于更多能群的边界条件修正方法有待进一步研究[15]。

为处理栅元均匀化环境效应，本文拟分析栅元均匀化群常数相对误差及各群栅元不连续因子相对重要性，建立基于最小二乘法的热群栅元不连续因子和堆芯中子学特征量之间的多项式函数关系，并基于C5G7基准题[16]和KAIST基准题[17]进行数值验证。

1 栅元等效均匀化常数分析

1.1 栅元均匀化常数分析

基于棋盘式多组件问题进行栅元均匀化群常数相对误差及各群栅元不连续因子相对重要性分析。棋盘式多组件问题如图1所示，其燃料组件来自于KAIST基准题。

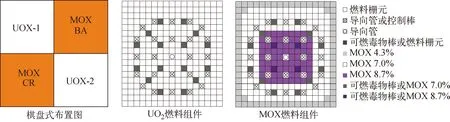
图1 棋盘式多组件问题Fig.1 Color-set problem

对棋盘式多组件问题进行了两类7群少群常数的计算：1) 参考解来自于棋盘式问题一步法计算，功率分布及7群栅元均匀化群常数考虑了不同类型燃料组件之间的干涉效应；2) 按全堆芯pin-by-pin两步法计算方案进行计算，首先进行全反射边界条件下的各类型单燃料组件计算，得到7群栅元均匀化截面，然后进行全堆芯计算获得功率分布。

图2为堆芯7群pin-by-pin计算的棒功率相对误差分布。可发现，最大棒功率相对误差出现在组件与组件交界面附近，这是由第2类计算方案中全反射边界条件与堆芯真实环境的差异导致的，交界面附近最大棒功率相对误差为4.03%，其余燃料棒相对误差在1%左右。

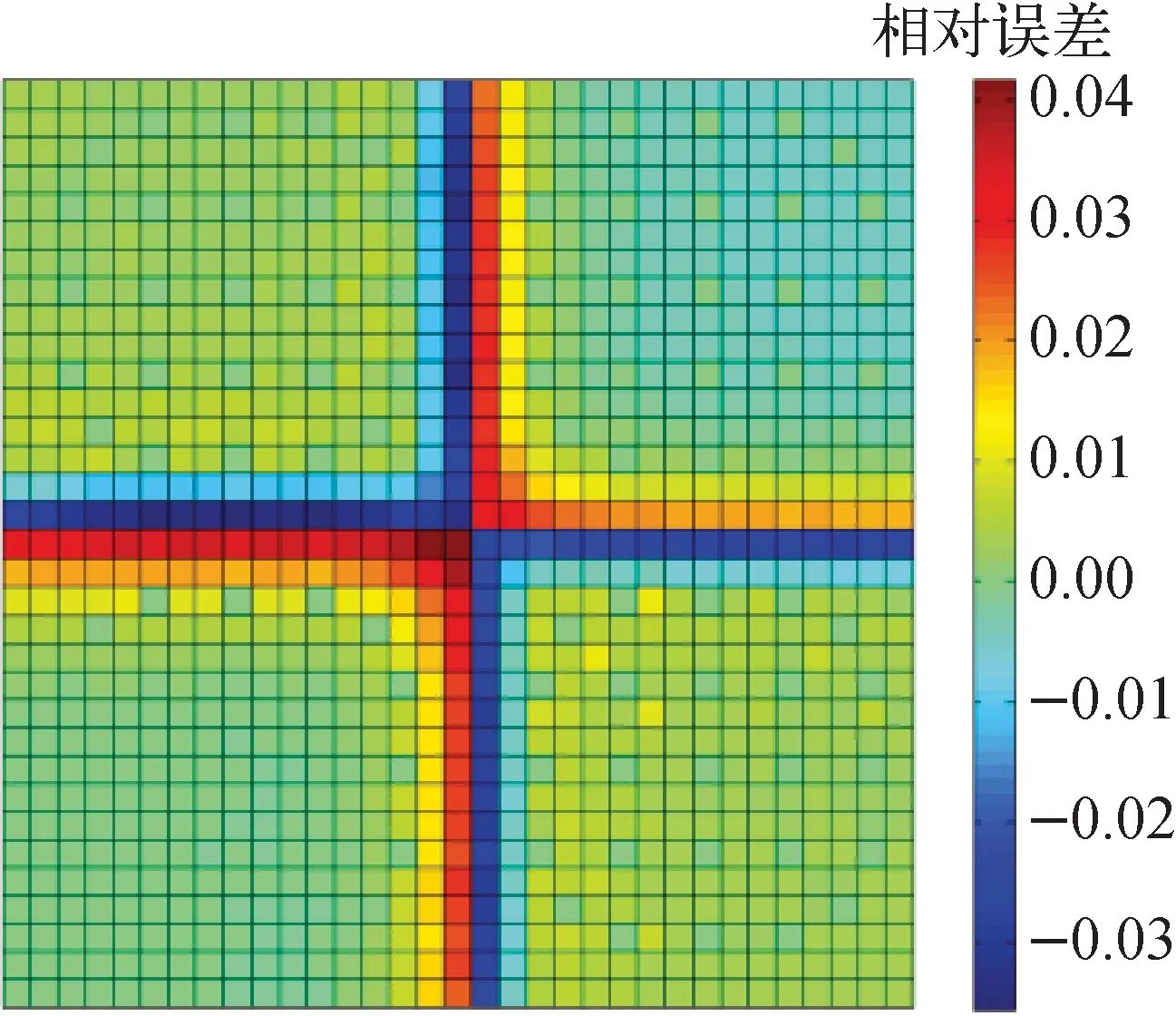
图2 棒功率相对误差分布Fig.2 Distribution of pin-power relative error

UO2和MOX燃料组件交界面附近各栅元编号及对应编号栅元归一化通量分布分别示于图3和4。可发现，热群(5～7群)通量之间的能谱干涉效应非常强烈，而快群(1～4群)中子能谱干涉效应相对较弱。

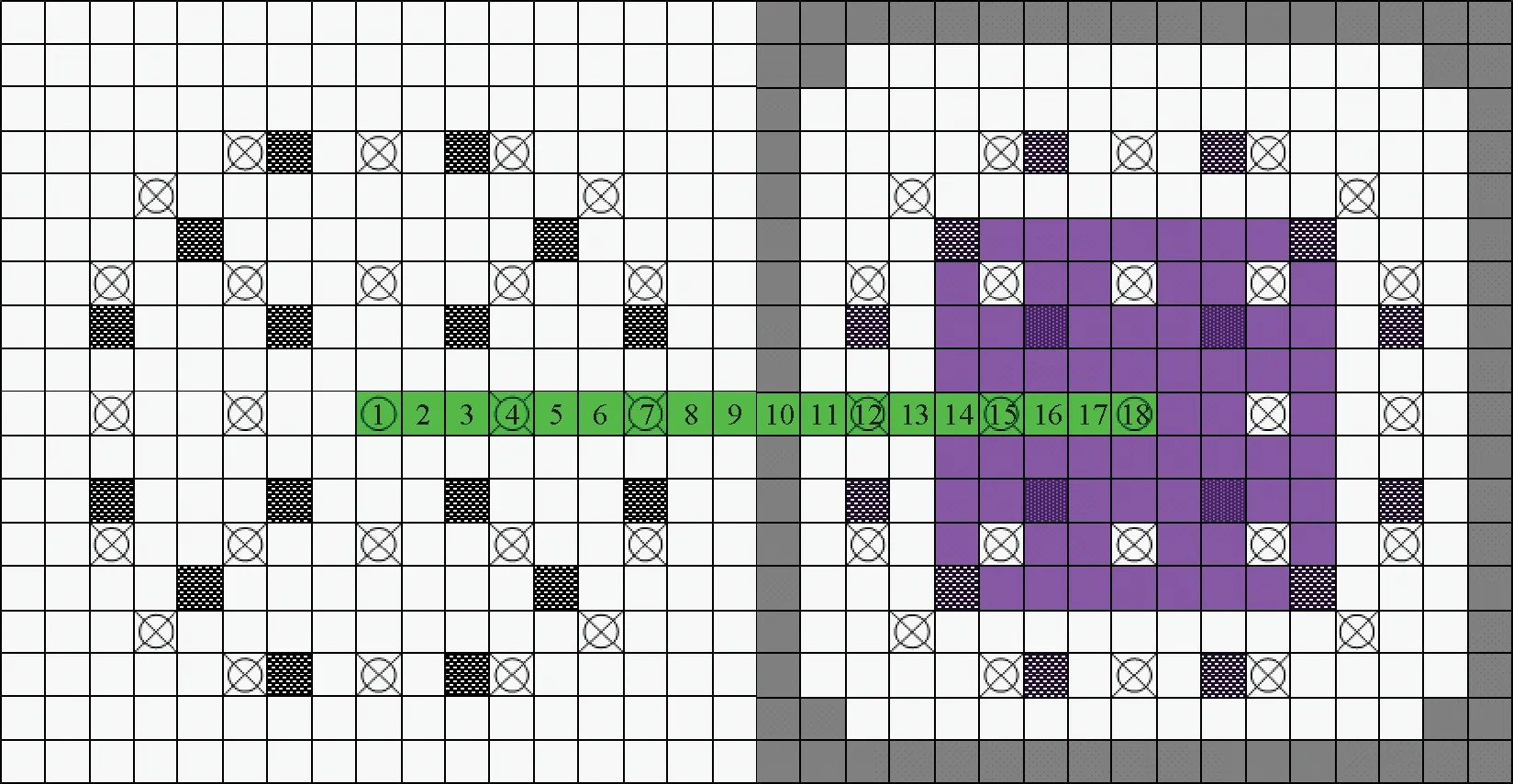
图3 不同位置处栅元编号Fig.3 Pin-cell number in different positions

部分均匀化截面及扩散系数与参考解的相对误差分布示于图5。可见，最大相对误差同样出现在组件与组件交界面上。尽管强烈的热群能谱干涉效应会导致边界上中子通量密度误差增大，但由于栅元均匀化截面是通过通量体积权重方法得到的，因此会减少均匀化截面的相对误差。对各能群各类型截面进行分析后可发现，均匀化截面的最大相对误差不超过1%。

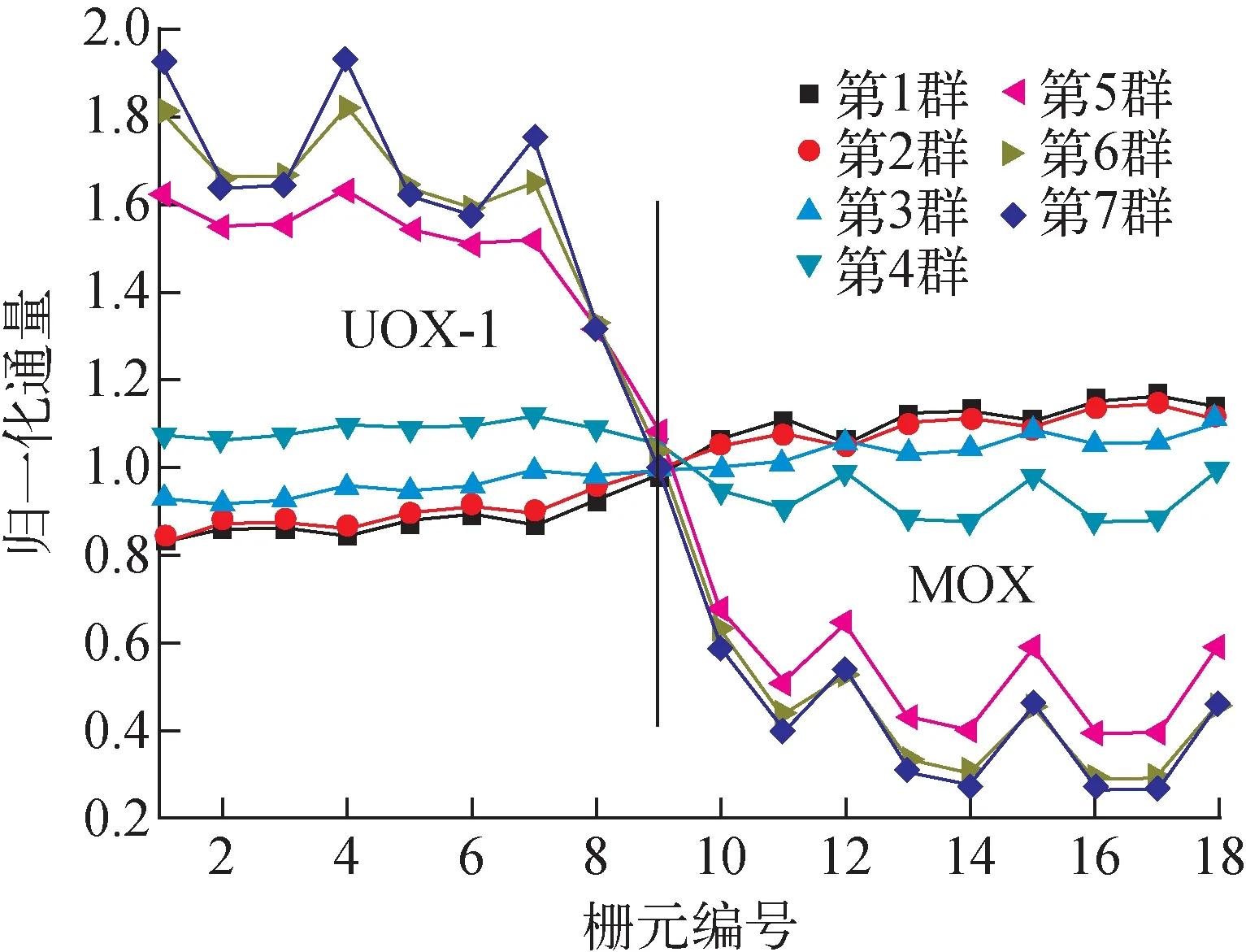
图4 编号栅元归一化通量分布Fig.4 Distribution of pin-cell flux

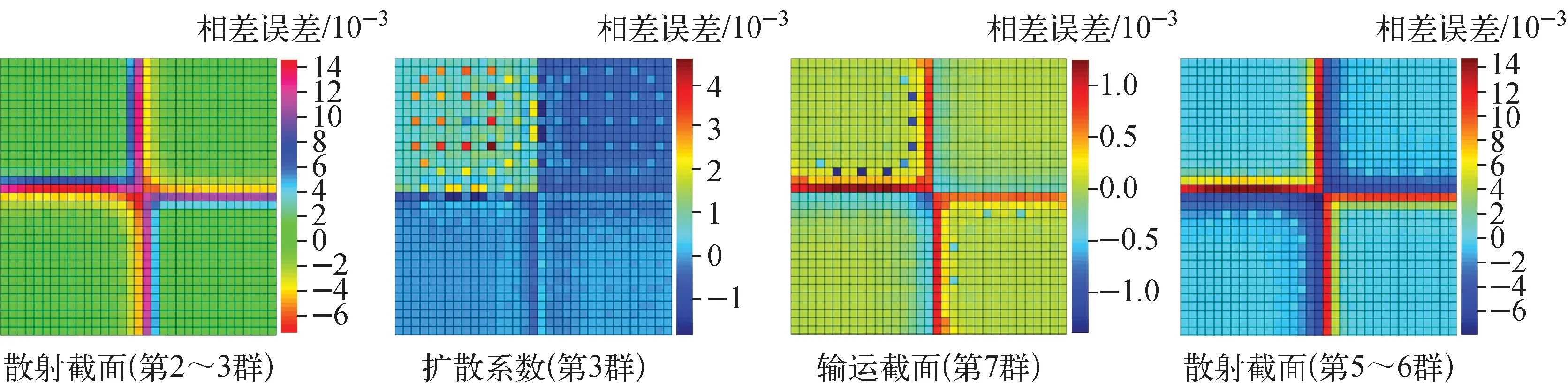
图5 部分均匀化常数相对误差分布Fig.5 Distribution of homogenized group constant relative error

组件内各栅元左侧面与右侧面不连续因子比值的相对误差如图6所示，图6中第1群与第7群分别代表快群中子与热群中子，不连续因子的参考解来自于全规模一步法计算。可发现，高能中子由于中子自由程长、干涉效应弱，全反射边界条件下快群中子的不连续因子误差很小，最大相对偏差小于1%；而热能中子由于中子自由程短、干涉效应强烈，全反射边界条件下热群不连续因子(PDF)最大相对误差为10.7%。

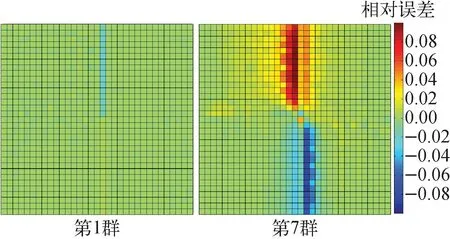
图6 栅元不连续因子相对误差分布Fig.6 Distribution of PDF relative error

根据均匀化截面、扩散系数和不连续因子分析结果可发现，pin-by-pin等效均匀化少群常数计算中，全反射边界条件对热群不连续因子带来的误差最大，处于组件外围的栅元热群不连续因子最大相对误差为10.7%，其余少群常数的相对误差低于1%。

1.2 栅元不连续因子重要性分析

为分析各群栅元不连续因子在压水堆堆芯计算中的相对重要性，对前文棋盘式问题中各单组件进行如下pin-by-pin计算：1) 不使用PDF(W/O)；2) 只使用热群PDF，快群PDF设为1.0(WT)；3) 只使用快群PDF，热群PDF为1.0(WF)。

栅元不连续因子的重要性分析计算结果列于表 1。表1结果表明：1) 任意能群的PDF都能提高pin-by-pin计算精度；2) 单独使用热群PDF的特征值误差和棒功率均方根误差均较单独使用快群PDF的误差小，且快群PDF提高的精度有限，因此热群PDF的相对重要性高于快群；3) 所有能群都不使用PDF的计算误差近似等于单独使用热群PDF和快群PDF的计算结果误差之和，这表明PDF在各能群间相互独立、效果叠加。

表1 栅元不连续因子重要性分析计算结果Table 1 Result of PDF importance analysis

2 热群常数堆芯在线计算方法

由前文可知，由于热群不连续因子相对误差较大且相对重要，因此热群不连续因子的计算准确性直接影响堆芯pin-by-pin计算的精度。本文基于最小二乘法建立热群栅元不连续因子和堆芯中子学特征量之间的多项式函数关系，利用参数化技术提出热群常数堆芯在线计算方法，其中堆芯中子学特征量包括扩散系数、移出截面、中子源项、归一化中子通量密度等。

热群不连续因子多项式函数形式如式(1)所示。

(1)

式中：f为热群不连续因子的函数形式；x为堆芯中子学特征量；a为展开系数；下标i、j、k为堆芯中子学特征量。

堆芯中子学特征量从中子泄漏、中子转移和中子产生这3种中子行为方式出发选取，本文堆芯中子学特征量选取如下：

(2)

式中：D为扩散系数；Σr，i，g为移出截面；Q为中子源项；E、W、S、N为栅元各边界。

压水堆堆芯中子行为在燃料组件和反射层组件中存在较大差异，热群不连续因子和本方法选定的堆芯中子学特征量同样存在很大差别。根据组件类型对热群常数堆芯在线计算所用的多项式函数进行分类可有效提升多项式函数的计算适用性，从而提高堆芯pin-by-pin计算精度。本文采用燃料组件和反射层组件两类热群不连续因子多项式函数进行热群常数堆芯在线计算。对于燃料组件，采用不同形式的各类型(1×1、1×2和2×2)燃料组件形成多项式拟合函数展开系数的计算数据集；对于反射层组件，采用不同形式的围板反射层组件形成多项式拟合函数展开系数的计算数据集，主要包括一维平板状围板、二维楔形围板。

3 数值计算与分析

本文采用C5G7基准题及KAIST基准题对热群常数堆芯在线计算方法的计算效果进行分析。

3.1 C5G7基准题

C5G7基准题堆芯布置如图7所示。以多群蒙特卡罗计算结果作为参考解，堆芯pin-by-pin计算结果列于表2，堆芯棒功率相对误差分布示于图8，其中LSM表示热群常数堆芯在线计算方法，SA表示单组件均匀化计算方法。

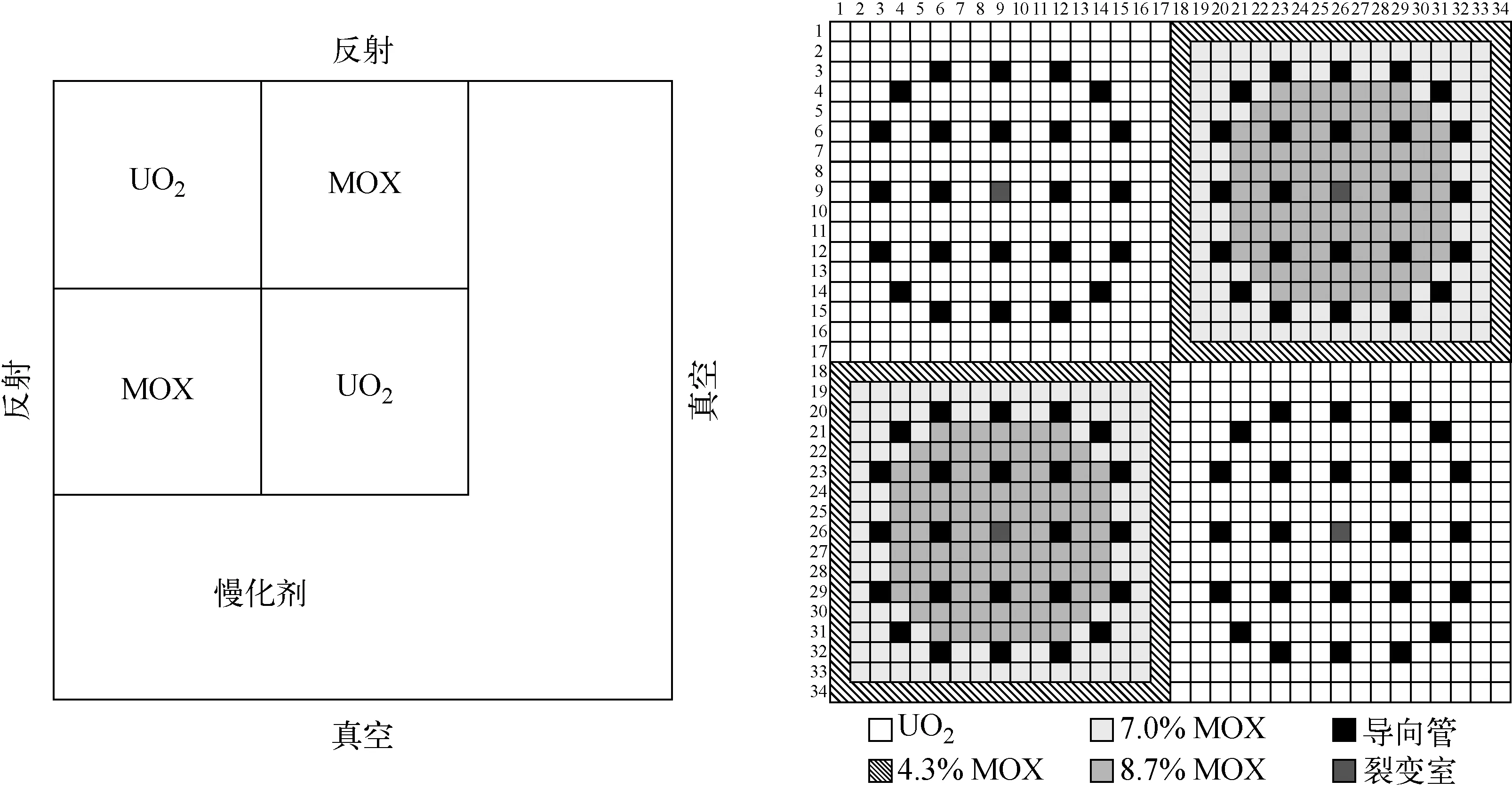
图7 C5G7基准题堆芯布置Fig.7 Core layout of C5G7 benchmark

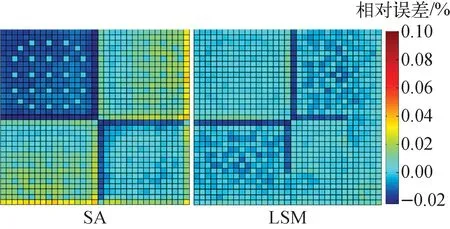
图8 C5G7基准题棒功率相对误差分布Fig.8 Distribution of pin-power relative error of C5G7 benchmark

表2 C5G7基准题计算结果Table 2 Result of C5G7 benchmark

3.2 KAIST基准题

KAIST基准题堆芯布置如图9所示，以MOC一步法计算结果作为参考解，堆芯pin-by-pin计算结果列于表3，堆芯棒功率相对误差分布示于图10。可见，热群常数堆芯在线计算方法在保持高精度特征值计算结果的同时，提高了棒功率计算精度，最大棒功率相对误差由3.29%降低为-2.13%，组件与组件交界面附近的棒功率计算精度明显提高。

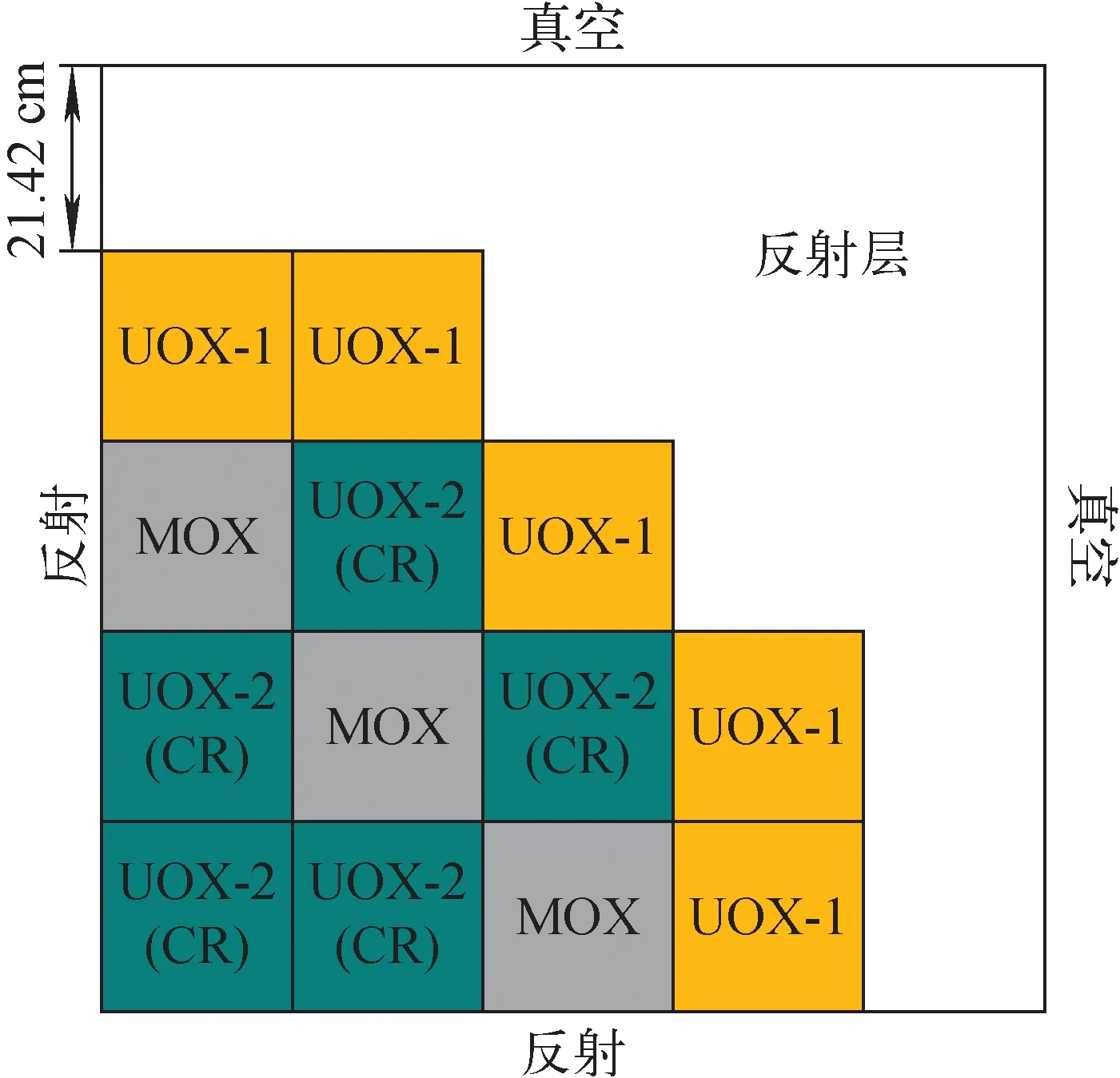
图9 KAIST基准题堆芯布置Fig.9 Core layout of KAIST benchmark

表3 KAIST基准题计算结果Table 3 Result of KAIST Benchmark

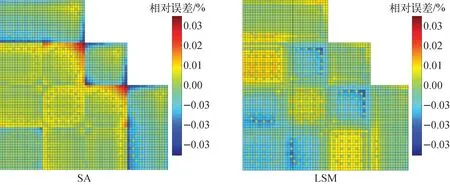
图10 KAIST基准题棒功率相对误差分布Fig.10 Distribution of pin-power relative error of KAIST benchmark

4 结论

本文基于棋盘式多组件问题分析了pin-by-pin均匀化中群常数误差及不同能群不连续因子的相对重要性。利用二维C5G7基准题和KAIST基准题，验证分析了热群常数堆芯在线计算方法的修正效果和计算精度。计算结果表明，热群常数堆芯在线计算方法有效降低了堆芯pin-by-pin计算误差，提高了堆芯计算精度。