基于三力汇交原理分析均质杆的平衡问题

慎晨乐 沈 卫

(湖州市菱湖中学 浙江 湖州 313018)

在高中阶段对于均质直杆的受力平衡问题往往采用力矩平衡结合共点力平衡的关系进行定量解析.但是考虑到高中阶段大多数的同学并不熟悉力矩平衡的概念及其规律，因此,在解决杆平衡的问题时不妨采用共点力平衡下的三力汇交原理来进行分析.如果均质直杆受到3个非平行力的作用而处于平衡状态，则这3个力必为共点力[1]，力的延长线必然相交于同一点.因此,对于两端受力的均质直杆而言，当3个力汇交于同一点后，可以对力所构成的平行四边形进行几何关系的定量分析.

1 共点力作用下分析直杆受力的几何方法呈现

当均质直杆两端受到互不平行力的作用而处于平衡状态时，依据三力汇交原理可以构建力的平行四边形.若平行四边形中存在直角三角形，则可从三角函数的关系着手列方程；若平行四边形中无直角三角形，则可从正弦定理着手列方程；当直杆的两端存在未知大小的力时(如杆的一端与铰链连接或者与粗糙地面接触等)，可以依据相似三角形边长的相似比相等列方程求解. 下面通过一个具体的问题实例来加以探讨.

【例1】如图1所示，质量分布均匀的直杆AB置于水平地面上，现在A端施加外力F，缓慢抬起直杆至竖直，B端始终和地面保持相对静止，F的方向始终和直杆垂直，要确保直杆B端始终和地面保持相对静止，则直杆和地面间的动摩擦因数至少为多少？

图1 外力F作用下的直杆AB

1.1 运用正弦定理列方程求解

直杆AB被缓慢地提起且B端静止不动，显然处于动态平衡状态，对其受力分析发现受重力mg和外力F以及地面的支持力与摩擦力(可合成为一个力F′)，且这些力的方向并不平行，因此力的延长线必然汇交于同一点，故可作受力分析图如图2所示.

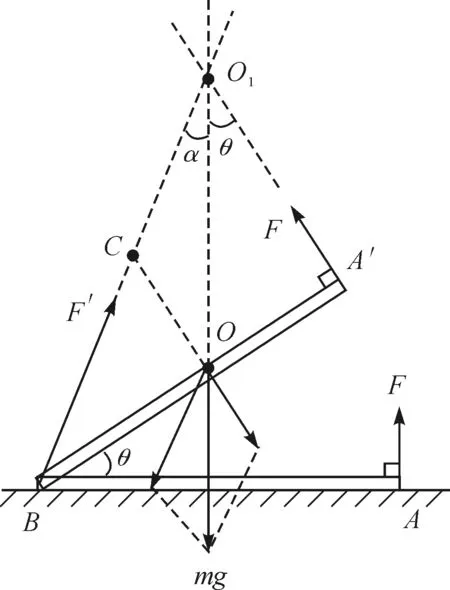
图2 直杆AB的受力分析图

根据图2，若B端始终与地面保持相对静止，则角α不能大于B端的摩擦角，即角α的正切值满足：tanα≤μ.

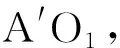
根据正弦定理，在△OCO1存在

(1)

其中OO1边和OC边的边长满足

(2)

联立表达式(1)、(2)，消去L可得

cosθsin(α+θ)=2sinα

对该式进行整理可将之转化为关于tanα的表达式

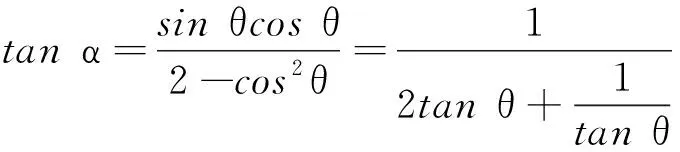
1.2 从相似三角形相似比的角度构建力的关系

既然△OCO1与直杆平衡状态下三力所构成的闭合三角形为相似三角形，则由边长的相似比可知

(3)

根据图2，在△A′BO1中存在

(4)

联立表达式(3)、(4)可得

因此，地面对直杆B端的支持力FN与摩擦力f满足

即

同样可得到动摩擦因数应满足的最小值.

可见要解决均质直杆在共点力作用下的平衡问题，如果要避开对力矩平衡关系的应用，则要充分渗透对三角形几何关系的运用.不仅要依靠正弦定理把握非直角三角形3力之间的定量关系，还要根据边角的相似特征(如杆的长度、杆与水平面的夹角等)找寻相似三角形，依据相似比建立方程，实现对力大小与方向的解析.

2 基于相似三角形关系深化方法的运用

利用三力汇交原理构建力矢量三角形的相似三角形，将对力大小的求解依托于相似三角形相似比的讨论中，并依据重力已知的条件，实现对直杆两端受力大小的求解.下面再通过一个问题的求解进一步对该方法的运用进行展示与深化.

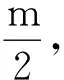
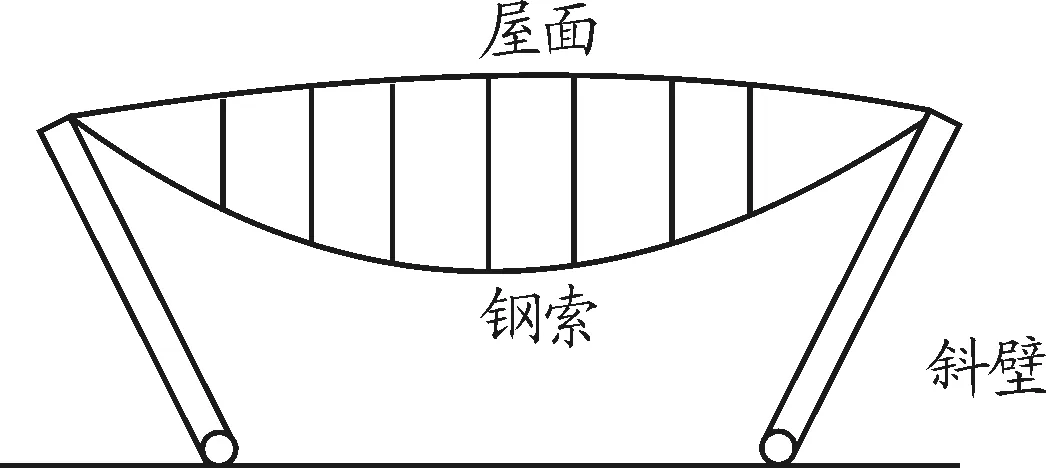
图3 机场候机楼的结构简图

分析：由对称性可对一侧的斜壁进行受力分析，其受力分析图如图4所示;将钢索与屋面看成整体，其受力分析图如图5所示.

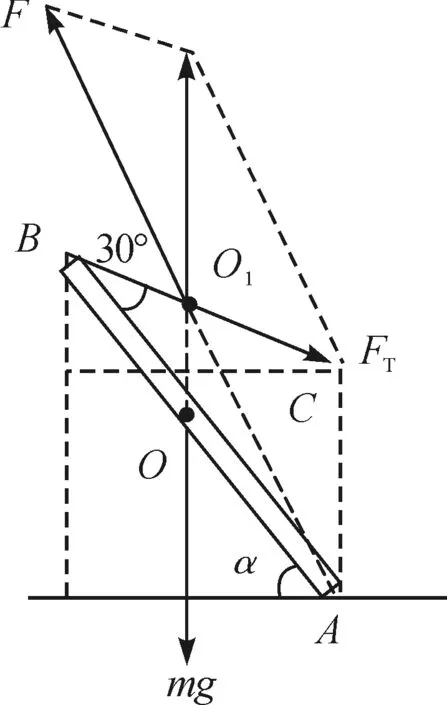
图4 斜壁的受力分析图

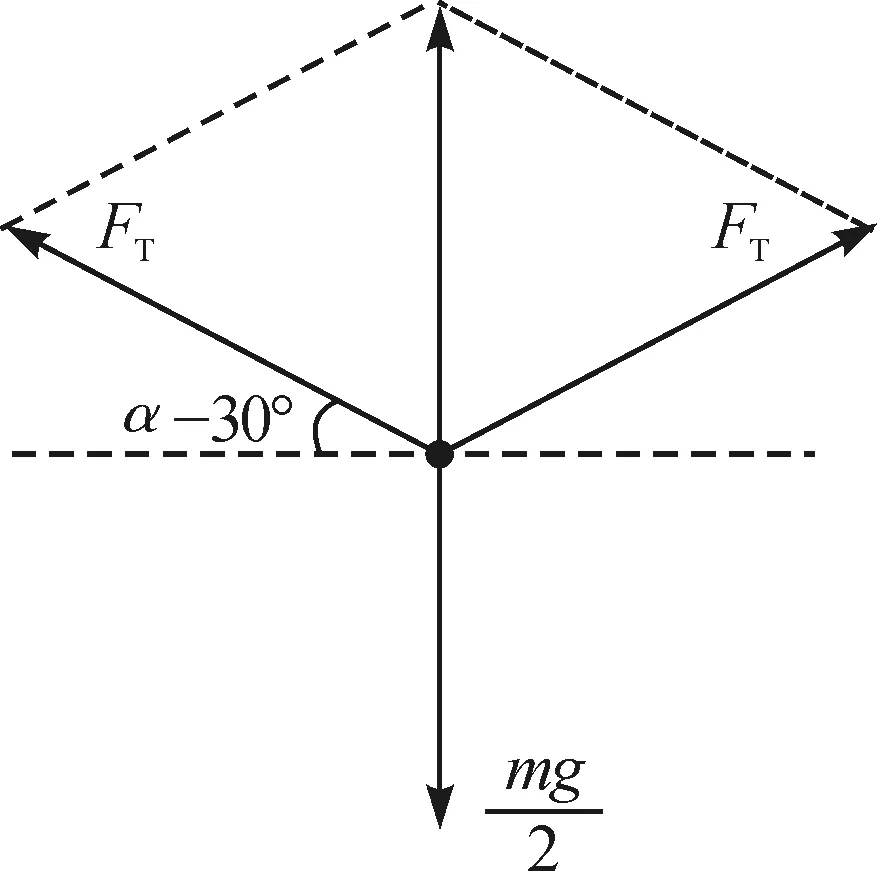
图5 钢索与屋面整体的受力分析图

取斜壁与地面的夹角为α，由图5可知斜壁对钢索的拉力FT满足

(5)

由图4中力的平行四边形定则可知，存在力的矢量三角形与△ACO1为相似三角形，因此,根据边长与力的相似比关系，可构建拉力FT与斜壁重力mg之间的关系为

(6)

取斜壁AB的长度为L，由边角的几何关系可知O1C边与CA边的边长满足

|CA|=Lsinα-Lcosαtan(α-30°)

(7)

联立表达式(5)～(7)并消去表达式中的L与mg整理得

3tan(α-30°)=tanα

由此可知斜壁与地面的夹角α=60°，斜壁对钢索的拉力为

依据三力汇交原理分析均质直杆的受力平衡问题所关联的还是高中阶段共点力平衡的力学知识，只是在问题解决中对知识与方法的运用有更高的要求，主要体现在：

(1)只有清晰、规范地展现物体的受力情况，才能从中发掘共性、形成关联，构建出问题解决所需要的等式与方程.因此,要引导同学们正确认识受力分析在解决力学问题中的功能与作用，使同学们明白受力分析不仅要会画受力分析图，还要画好受力分析图(包括作图习惯的养成、作图规范的生成、作图工具的运用等).

(2)对三角几何知识的运用有更高的要求，不仅体现在使同学们能够处理与直角三角形有关的力平衡问题，更多的情况下是对非直角三角形平衡关系的定量分析.这就需要同学们在平时的学习中注重学科间知识的迁移与结合，拓宽方法运用的“临界点”，使中学数学知识更好地、更有效地用于对物理问题的分析与解决.