含电动汽车虚拟电厂的区间 主从博弈优化调度

华远鹏，王圆圆，白宏坤，韩 丁，卜飞飞，王 涵，贾一博

（国网河南省电力公司经济技术研究院，河南 郑州 450000）

我国力争于2030年前实现二氧化碳排放达峰，单位国内生产总值二氧化碳排放将比2005年下降65%以上，在2060年前实现碳中和。“双碳”背景下，电动汽车数量将大幅增加[1-3]。电动汽车充电负荷具有较强的随机性，大规模电动汽车无序充电必将加剧局部电网供需不平衡。将规模化电动汽车进行聚合和有序调度，以发挥其储能潜力，是当前能源利用研究的热点。以虚拟电厂（virtual power plant，VPP）为例，通过对电动汽车充放电的合理调度，可为电网安全、经济运行提供重要保障[4-5]。

众多学者已对电动汽车参与需求侧响应开展了相关研究。文献[6]为解决电动汽车用户基于电价响应所致的峰谷倒置现象以及多次充电造成的电池损耗等问题，建立了在上层考虑电网收益、在下层考虑电池损耗的主从博弈模型，以兼顾双方利益减少负荷峰谷差。为解决电动汽车和空调的规模化接入使得配电网尖峰负荷持续增大的问题，文献[7]建立考虑电网公司与电动汽车代理商、储能运营商的主从博弈模型，上层构建运营收益最大与峰谷差最小的多目标函数，下层以用户收益最大为目标。文献[8]为实现代理商与电动汽车主间的双赢，提出一种智能小区代理商的定价及购电策略。文献[9]建立了以用户需求偏好的并网电动汽车控制模型，在时间、空间、功率3个维度构造多面体不确定集合，采用交替方向乘子法实现了模型的分布式迭代求解。文献[10]利用电动汽车的时空分布特性，用户温度负荷的柔性特点，建立多种规划模型，通过对模型的分析，有效减少了消纳可再生能源所需的实体储能配置容量。文献[11]提出了一种基于Stackelberg博弈的电动汽车光伏充电站动态定价方案，该模型还引入了反映电动汽车充电连续性引起的功耗波动的约束，通过分析约束的概率性质，将不确定性博弈模型等价转化为凸博弈，所提定价方案能够较好地降低充电站的销售价格，提高充电站的利润。文献[12]提出了一种利用Stackelberg博弈来模拟服务提供者和服务请求者之间交互的最优定价策略。文献[13]利用Stackelberg差分博弈来模拟智能电网中电动汽车的充电控制问题；在所建差分博弈模型中，集合体作为领导者，根据均衡方案确定最佳电力交易价格，电动汽车作为追随者，控制其充电功率，最小化能源交易成本。文献[14]建立了微网与用户间的Stackelberg博弈模型，将电动汽车用作分布式储能，参与电力交易。将保持供需平衡和最大利润作为上层微网目标，将最高的电力消费满意度和最低的能源成本作为下层用户目标。上述研究已将博弈思想引入电动汽车的充放电问题，但是，在虚拟电厂中，各分布式电源出力、负荷均具有较强的不确定性，如何简单有效描述这些不确定性因素，并在优化调度过程中予以充分考虑，是亟需解决的问题。

基于此，本文引入区间数方法描述虚拟电厂、源、荷的不确定性，并与博弈论相融合，提出一种含电动汽车的虚拟电厂区间主从博弈双层优化模型。在上层，建立以虚拟电厂运营商成本最低的优化模型；在下层，考虑电动汽车的随机性，建立以电动汽车用户充电费用最小的优化模型，从而基于区间主从博弈求得最优调度方案。所得调度方案能够兼顾电厂运营商与电动汽车主的双边利益，具有较好的鲁棒性，能够较好地克服源、荷不确定性因素对调度过程的影响。

1 含电动汽车的区间主从博弈架构

本文考虑虚拟电厂运营商与电动汽车车主间的博弈关系，提出一种基于区间数的双层优化模型：上层考虑光伏发电出力、风力发电出力、刚性负荷与电动汽车负荷的不确定性，利用区间数描述其随机波动性，建立以虚拟电厂运营商运营成本最小的优化模型；下层利用蒙特卡罗法模拟电动汽车出行规律的随机性，建立以电动汽车车主充放电成本最小的下层优化模型，双边反复博弈以求得纳什均衡解。所建立区间主从博弈模型架构如图1所示。

2 不确定因素描述

2.1 区间优化理论

式中：x为决策变量；Ω为决策空间；c为区间向量，有c=(c1,c2,…,cL)T，对于，其中、分别为ci的下限与上限；gj(x,c)≥aj为区间不等式的约束条件；hk(x,c)=bk为区间等式约束条件。从决策空间到目标空间的映射由M个目标函数组成，fI(x,c)为目标函数，因含有区间向量c，其取值亦为一区间数。

因此，区间多目标优化问题本质上为一个2层优化问题，外层优化问题决策变量为x，内层优化问题决策变量为y。

2.2 区间变量设置

区间可信度具有如下性质：

1）P(a≥b) +P(b≥a)=1；

2）P(a≥b) ≥ 0.5，当且仅当，或者等价于m(a) ≥m(b)。

对于区间不等式约束gj(x,c)≥aj，记个体x满足该约束条件的可信度为：

相应地，记个体x不满足该约束条件的可信度（个体x对该约束的违背度）为：

本文将个体x满足每一约束条件的可信度与设置的可信度阈值δ*j比较，从而判断其是否为可行解，即若对于任一约束条件gj(x,c)≥aj，均有，则称x为可行解；否则，称x为非可行解。

由上述区间可信度分别建立区间[PPV]、[PWT]、[Pload]、[PEV,sum]（式(8)—式(11)）分别表示光伏发电功率、风力发电功率、刚性负荷与电动汽车负荷等不确定因素的随机波动范围，构成区间向量c=([PPV], [PWT], [Pload], [PEV,sum])T。从概率角度分析，可认为上述不确定因素均围绕其预测值随机波动，并具有对称性。

式中：PPV0(t)、PWT0(t)、Pload0(t)、PEV,sum0(t)分别为t时段光伏发电功率、风力发电功率、刚性负荷以及电动汽车充电功率的日前预测结果；ΔPPV(t)、ΔPWT(t)、ΔPload(t)、ΔPEV,sum(t)分别为各预测结果不确定的波动幅度。

3 博弈模型建立

图2为所建立含电动汽车的区间主从博弈模型结构。

由图2可见，模型考虑虚拟电厂运营商与电动汽车主间的博弈关系，基于文献[13-15]并结合区间优化思想建立区间双层博弈模型，上层虚拟电厂运营商通过制定相应的电价政策引导电动汽车进行合理充放电以使自身收益最大，在上层制定的电价策略基础上，下层通过改变电动汽车的充放电行为，实现自身充电费用最小，并将所求得的充电用电行为曲线返回至上层模型，上层模型在考虑其充电行为的随机波动与源荷预测偏差的情况下，重新制定相应的电价策略，如此反复，直至求得最终的博弈均衡解。

3.1 上层虚拟电厂运行商优化模型

3.1.1 上层目标函数

上层虚拟电厂运营商作为枢纽连接上级电网与下层电动汽车负荷用户，运营商考虑源荷不确定性建立以运营商运行成本最低的上层优化模型，其目标函数为：

式中：f1为上层虚拟电厂运行成本；CGrid+(t)、CGrid-(t)分别为与上级电网交互电价；cbuy(t)为电动汽车充放电费用；[Pgrid(t)]、[PEV,sum(t)]为考虑不确定因素与上级电网交互功率及电动汽车聚合功率。

3.1.2 功率平衡条件

3.1.3 储能设备约束

储能系统具有响应快速性的特点，在保证供电可靠性的同时，可通过合理安排充放电时间使得运行目标最优，其模型如下：

式中：Psi,max、Psi,min分别为储能系统充放电功率上、下限；ηc、ηdisc分别为储能系统充、放电效率；SSOC,max、SSOC,min分别为储能系统荷电量上、下限。

3.2 下层电动汽车主体优化模型

3.2.1 下层目标函数

3.2.2 电动汽车聚合模型

电动汽车聚合时考虑出行规律的随机性，利用蒙特卡罗抽样依次对出行时间、返回时间、行驶里程等3个函数进行抽样以模拟电动汽车随机出行规律，下面针对第i辆电动汽车建立如下模型：

式中：SSOCEV(t)为t时段第i辆车的电池电量约束；SSOCEV,last,i(t)为第i辆车出行时刻电量；Ci为第i辆车的电池容量。式(18)—式(21)为第i辆电动汽车约束；式(22)为聚合电动汽车功率；式(23)为电动汽车聚合功率区间波动范围，波动系数取0.1，为最大波动幅度除以该时刻对应的荷侧出力。

为更好地模拟电动汽车出行规律的随机性特点，利用蒙特卡罗法对居民区的电动汽车出行分布函数进行抽样，其分布函数为：

式中：th为住宅区用户返程时间；μt为期望值，取17.6；σt为标准差，取3.4。

4 模型求解方法

粒子群算法因其算法原理简单、收敛速度快、需调整参数较少，且具有一定的记忆性和进步性，能完整保存迭代过程中粒子的全局与局部最优解，对分析博弈互动过程具有一定帮助[15-17]。通过引入区间可信度，将上层区间优化不确定性模型转化为确定性模型，所建立的博弈上下层模型利用Yalmip工具箱中的Cplex求解器以实现对上下层适应度函数的快速准确求解，博弈模型求解流程如图3所示。具体步骤为：

1）建立考虑源荷不确定性的各层主体能量管理模型，并设置粒子数量迭代次数以及相应的博弈收敛误差；

2）随机初始化粒子群算法参数，生成电价信息初始粒子；

3）下层电动汽车用户根据电价利用Cplex求解下层模型，求得最优用电行为；

4）上层虚拟电厂运营商依据下层用户用电行为在考虑预测不确定性的基础上，将聚合电动汽车区间与电价信息代入上层优化模型，通过合理调控储能系统实现其虚拟电厂运行成本最低；

5）以上层虚拟电厂运营商成本最小作为粒子适应度函数目标值，基于所设置参数更新粒子的速度和位置；

6）判断是否达到最大迭代次数，或比较与前一轮迭代的最优结果值，其差值若小于精度则为博弈均衡解；

7）若未达到博弈次数，则重复上述步骤3)—步骤6)。

5 算例分析

选取某实际典型虚拟电厂为研究对象，进行算例分析。该虚拟电厂光伏发电装机容量1 800 kW，风力发电装机容量为2 500 kW，储能系统额定容量为750 kVA，包括电动汽车200辆。基于区间数描述源荷随机波动如图4—图7所示。

各设备具体参数以及相应的源荷波动区间见表1。源侧不确定性利用波动系数进行描述，指最大波动幅度除以该时刻对应的源侧出力。在荷侧电动汽车基于典型住宅区出行规律曲线，利用蒙特卡罗法模拟该园区各区域200辆电动汽车随机出行规律，并求得聚合后电动汽车功率利用区间送至上层模型。

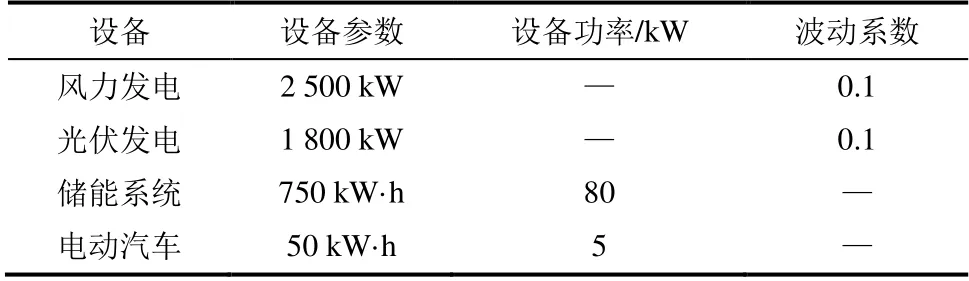
表1 设备参数 Tab.1 Equipment parameters

基于第4节结合粒子群的Cplex求解方法，对所建立的虚拟电厂运营商与电动汽车用户主体间的区间双层博弈模型进行求解，设置粒子种群数为30，迭代上限为60，区间可信度设为0.9，上层、下层模型的适应度函数收敛结果如图8所示。由 图8可见，以目标函数区间中点作为上、下层目标函数值，通过两方的博弈，上下层函数均呈收敛趋势，即虚拟电厂运营商层运行成本逐渐降低，下层电动汽车负荷用电成本呈下降趋势。在迭代50次左右，上下层函数趋于稳定，说明得到博弈均衡解，从而证明所建立博弈模型的有效性。

上层区间优化模型的目标函数随迭代次数的收敛变化区间如图9所示。由图9可见，其趋势与上层迭代收敛次数趋势相同，在目标函数趋于稳定时，其目标函数上边界维持在7 253元，下边界维持在-5 000元。

在迭代达到纳什均衡解时，所求得博弈电价如图10所示。图10虚线为所设电动汽车充放电电价上下限，实线为所求得的博弈电价曲线。由图10可见，因所建立模型考虑源荷的不确定性，所求得调度方案具有较高的鲁棒性。为应对源荷波动，时间在00:00—08:00时，博弈电价位于中偏上；在05:00时风力发电达到上限，可再生能源出力远大于负荷，此时并网售电价格较低，引导电动汽车充电以消纳过剩的可再生能源，取所设置电价下限；其余时刻为减小自身成本，同时克服源荷的随机波动，博弈电价均取电价上下限之间。

图11为电网交互功率区间。由图11可见，电网交互功率趋势、可再生能源发电以及刚性负荷与图7电网电价相关。即在06:00及12:00可再生能源出力较多，同时电网电价较高，高于博弈价格上限，此时博弈电价取电价上边界附近以减少电动汽车消纳，过剩可再生能源多送至电网消纳；在00:00—05:00时段与21:00—23:00时段电网电价较低，此时以向电网购电为主，在考虑区间波动后所求得联络线曲线可为台区变压器容量设置提供相应指导。

图12为储能系统充放电功率。由图12可见，为应对源荷不确定性，提高系统运行可靠性，储能系统充放电功率与上级电网交互功率价格曲线趋势相同。即在电价较高时段放电，在电价较低时段充电，以降低虚拟电厂运营商的运营成本。

图13为聚合电动汽车充放电功率曲线后加随机波动所得电动汽车充电区间。算例设置抽样函数为住宅区电动汽车分布函数，故其返回时刻集中在16:00—19:00时段，离开时刻集中在08:00—10:00时段，以满足住宅区居民生活习惯；其余时刻无电动汽车可进行调度，故其曲线在11:00—15:00时段聚合功率为0。在可调度时段电动汽车充放电行为与图10博弈电价曲线趋势相同，即在电价较高时进行放电或不进行充电，在电价较低时进行充电以实现下层电动汽车用户用电成本最小。由图13可见：23:00—05:00时段，此时充电价格设置较低，故多数电动汽车主选择此时进行充电；在17:00—21:00时段博弈电价较高，住宅区抽样电动汽车陆续返回，电动汽车车主为减少自身充放电成本可进行放电。不同电价时段各设备性能对比见表2。

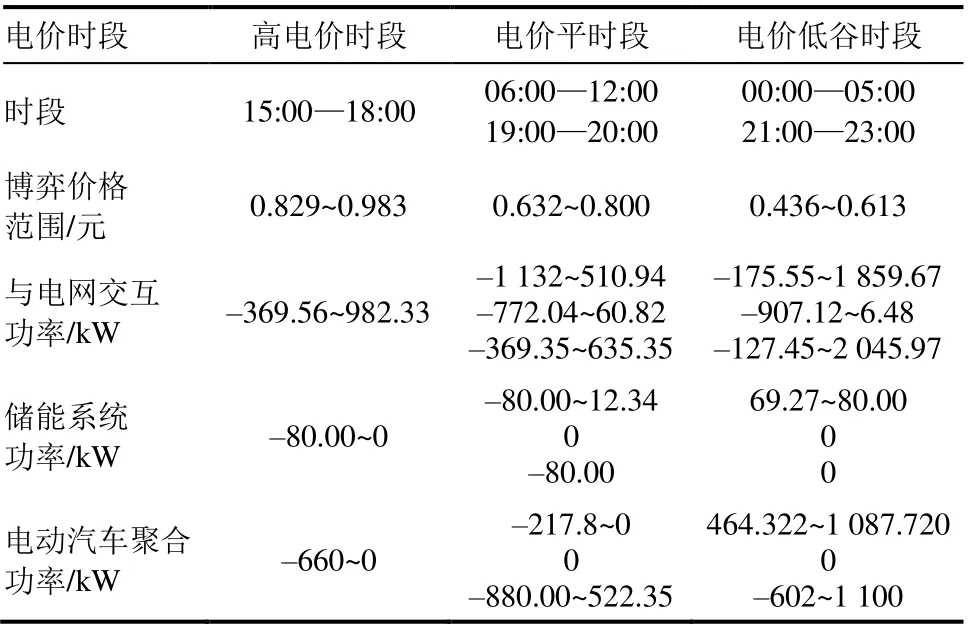
表2 不同电价时段各设备性能对比 Tab.2 Comparasion of device performance in different electricity price time segments

6 结 论

1）提出了一种含电动汽车虚拟电厂的区间主从博弈双层优化模型，以虚拟电厂运营商运行成本最低为上层优化模型，以电动汽车主充电费用最低为下层模型，为更好地模拟博弈过程，采用结合粒子群与Cplex的求解方法求解博弈模型。通过对电价以及电动汽车充电功率反复调整，即经过多次博弈，求得纳什均衡解，可实现虚拟电厂运营商与电动汽车主的利益均衡。

2）在源荷建模上更贴近实际，引入区间数描述源荷的随机波动，使所求调度方案更具鲁棒性。在求解方法上，利用结合粒子群与Cplex的求解方法，可以快速有效地获取纳什均衡解。

3）通过求解所建立区间主从博弈模型，可得出电网交互功率区间受博弈电价与可再生能源出力影响，蓄电池出力受上级电网交互功率电价曲线趋势影响，电动汽车聚合功率曲线则受所求得博弈电价影响；算例结果可为虚拟电厂提供更具鲁棒性的电价制定策略。