基于非支配排序遗传算法和多目标粒子群 算法的脱硫系统运行策略优化

李兆北，王印松，苏 杰

（华北电力大学自动化系，河北 保定 071003）

电力在国民生产生活中发挥着重要作用，根据国家能源局发布的《2020年全国电力工业统计》数据显示，我国2020年火电装机容量约占总装机容量的56.58%[1]，以煤炭为能源的火电在我国电力结构里仍将占据主导地位。石灰石-石膏湿法烟气脱硫（wet flue gas desulfurization，WFGD）是目前使用最为广泛的烟气脱硫方法，随着工艺水平的提升，当前污染物脱除装置的脱除效率已达到较高水平，WFGD的脱硫效率已达97%[2]。为了满足超低排放要求，烟气脱硫过程中人工操作会过量投入物料或加大设备运行功率，致使运行成本过高。如何使烟气污染物排放稳定达标的同时，实现污染物脱除装置的经济运行成为当前研究的重要课题。

脱硫系统运行优化已经得到研究者的普遍重视。不少学者从反应机理和运行特性入手，建立脱硫系统的机理模型并实现系统优化[3-5]。但机理建模过程通常以理想状态为标准，对模型进行了假设与简化，无法准确描述复杂过程，在实际应用中会受到一定的限制。采用数据驱动的方法建模能有效解决这些问题，厂级监控信息系统(supervisory infor-mation system，SIS)中海量的历史数据也为数据建模提供了便利[6-8]。顾慧等[9]提出信息熵理论结合K均值和模糊c均值的EKFCM算法，并将其应用于脱硫运行目标工况库的建立。徐哲炜等[10]提出一种改进型关联规则算法，并应用于燃煤电厂脱硫系统的工况参数优化，实现污染物出口浓度达标的前提下降低能耗物耗。上述2种方法只能在稳态负荷下分析出最佳工况参数，在变负荷条件下无法给出指导。Guo等人[11]采用机理与数据混合方法建立出口SO2浓度预测模型，并与运行成本模型组成混合模型，采用粒子群（PSO）算法实现对WFGD系统操纵量参数的优化。但该优化算法容易陷入局部最优而无法找到全局最优解。黄悦琪[12]采用动态罚函数的方法描述环境成本，将双目标受约束问题转换为单目标问题，再利用改进变异PSO算法寻优得到操纵量参数的最优设定值。但是该方法鲁棒性差，处理复杂特性问题效果较差，在实际运用中效果不佳[13]。

针对运行成本和环境成本相互制约以及寻优过程容易陷入局部最优的问题，本文提出一种结合非支配排序遗传算法-II（non-dominated sorting genetic algorithm II，NSGA II）和多目标粒子群（multi-objective particle swarm optimization，MOPSO）算法的混合NSGA II-MOPSO算法。相较于传统方法，该混合算法结合了2种算法的优点，得到的Pareto最优解集能够呈现给决策者尽可能多更具有代表性的非劣解，避免陷入局部最优。将该算法与运行成本模型和出口污染物质量浓度预测模型结合建立混合优化模型，最终在可行域内的Pareto最优解集中得到变工况下的最优可变操纵量参数设定值，可为运行人员提供必要的指导。

1 脱硫系统优化模型

建立脱硫系统的精确模型是脱硫过程得到控制与优化的前提。脱硫系统在日常运行中以降低运行成本和污染物排放达标为目标。针对这2个目标，通过优化脱硫系统运行策略使其尽可能贴近理 想状态。

1.1 目标函数数学模型的建立

1.1.1 混合优化模型

以某660 MW燃煤机组脱硫系统历史数据为研究对象，原脱硫控制系统通过人工操纵pH值设定值和浆液循环泵开启台数确保日常运行中出口SO2质量浓度不超限。其中吸收塔浆液pH值的调节通过对吸收塔测量pH值与设定值进行比较，经系数修正后（高值时乘以0.9，低值时乘以1.1，在±10%范围内调整），对石灰石浆液流量进行修正调整。

为了能够根据变化的工况条件给出相应的可变操纵量设定值，本文结合现有脱硫控制系统设计了一种混合优化模型，模型结构如图1所示。

由图1可见，该模型在分散控制系统（DCS）中采集脱硫系统的实时工况条件（负荷、入口SO2质量浓度等）和各设备的电流电压，并与自变量数据（可变操纵量pH值和浆液循环泵开启台数）一起传入模型。通过出口质量浓度预测模型和运行成本模型计算对应的出口预测质量浓度和系统运行成本，再通过优化算法计算当前工况条件下最佳的可变操纵量参数设定值代替人工设定，实现脱硫系统经济高效的运行。

1.1.2 运行成本模型

脱硫系统运行成本以电耗与物耗为主，为了更全面地评价脱硫系统的经济成本，建立脱硫系统度电成本评价指标，即机组脱硫系统每度电产生的运行成本，同时根据脱硫系统脱除流程建立电耗和物耗成本计算模型。

电耗成本主要由脱硫系统的电机设备产生，包括氧化风机电耗、增压风机电耗、浆液循环泵电耗等。氧化风机、增压风机日常运行中是以主备组合、定期切换的方式运行，运行成本不受可变操纵量影响。脱硫系统电耗成本计算模型[14]为：

式中：Cscp、Cbf、Cfa分别为浆液循环泵、增压风机、氧化风机的电耗，下标scp、bf、fa分别表示浆液循环泵、增压风机、氧化风机；q为锅炉实时负荷，MW；Np为浆液循环泵的运行台数；Ui、Ii分别为第i台设备的电压与电流，kV、A；cosϕ为功率因数，一般取0.8；PE为电价。

物耗成本主要为脱硫吸收剂即纯度较高的CaCO3，通过与水混合形成石灰石浆液。根据物料平衡，其单位发电量成本为：

式中：C(CaCO3)为石灰石单价，价格受品质和市场影响；Q(CaCO3)为石灰石消耗量，t/h，其中石灰石消耗量和吸收塔浆液pH值有极高的相关性，采用Curve Fitting工具箱拟合建立两者的函数关系；除石灰石消耗外，物耗还包括水耗，脱硫系统水耗主要包括制浆的工艺水和设备冲洗水，水耗在整体成本中仅占1%～2%，影响很小，可以忽略不计。

综上所述，石灰石-石膏湿法脱硫的总体运行成本可表示为：

该成本函数通过当前的实时工况和可变操纵量参数，可以计算出脱硫系统当前运行策略的度电成本。

1.1.3 SO2质量浓度预测模型

本文使用SIS存储的脱硫系统历史数据建立出口污染物质量浓度预测模型。选取660 MW燃煤机组48 h数据，每20 s取一组共8 589组数据，通过数据预处理去掉异常点219组，最终数据8 370组。选取前6 000组数据作为训练集，后2 370组数据作为验证集。

SO2脱除过程具有不确定性、非线性以及变量间的关联性等特性，采用径向基函数（RBF）神经网络建立出口SO2质量浓度预测模型，就是要利用RBF神经网络的拓扑结构简单、学习速率快和克服局部收敛等特点，找出输入与输出的映射关系。

通过Pearson相关性分析选取入口SO2质量浓度、入口烟气流量、入口烟气温度、脱硫塔pH值、脱硫塔浆液循环泵开启台数和烟气氧量作为预测模型的特征变量。采用newrb构建有效的径向基函数网络，分布密度初设为1，训练精度设为0.001。图2为在验证集上预测值与实际值对比，图3为在验证集上预测值与实际值的对应关系。

该预测模型在变负荷条件下取得了较高的预测精度，其中均方根误差δRMSE为0.812；决定系数R2为0.920 2，说明该SO2质量浓度预测模型在变工况条件下误差较小、精度较高，在验证集上表现出令人满意的预测性能，可以作为脱硫系统出口SO2排放的预测模型。

综上所述，脱硫系统优化模型的数学表达式为：

式中：X=(pH,Np)为可变操纵量集合；f1(X)为系统运行成本模型，评价系统经济性；f2(X)为污染物排放模型，评价系统环保性。

1.2 约束条件

可变操纵量会受到现场实际情况的约束。脱硫塔内pH值过低会造成反应效率的下降，而过高的pH值会抑制副产物CaSO3的氧化和石灰石的溶解，导致副产品中出现大量难以脱水的CaSO3和石灰石颗粒，降低石灰石利用率。所以根据现场经验，实际运行中pH值的范围在5.0～6.2[9]。

浆液循环泵台数Np必须符合机组实际情况，在参数优化过程中只能取整数1、2、3。

2 混合NSGA II-MOPSO算法

NSGA II算法针对NSGA的不足主要提出了 3点改进：1）快速非支配排序策略；2）精英保留策略；3）拥挤度比较算子取代共享参数[15]。该算法具有鲁棒性能好、搜索能力强等优点；MOPSO算法主要任务包括线性调整惯性权重、外部档案维护、个体最优位置更新等[16]，具有收敛速度快，收敛精度高、搜索效率高等优点。本文将2种算法的优点结合起来，采用一种混合NSGA II-MOPSO算法，混合算法中的NSGA II算法部分沿用文献[15]方法，MOPSO算法部分为解决易陷入局部最优的问题而对极值选取和变异策略进行改进。

2.1 粒子个体和全局极值的选取

个体极值的选取前期采取“不支配则不更新”的原则，即仅在出现新的支配当前个体极值的粒子时更新个体极值，否则一直不变。

全局极值的选取采用自适应网格法[17]，将m维的外部档案划分成网格，一维上网格的个数为nGRID。则每个网格的第i维目标宽度di表达式为：

记录每个粒子所在网格的索引，通过比较计算出每个网格内粒子的个数ni，网格中粒子的分散程度Q表达式为：

选择分散程度最大的网格，并在其中随机选取一个粒子作为极值GBEST。这样，在粒子密度低的网格中选取全局极值GBEST去引导的下一轮迭代，能够有效避免陷入局部最优。

2.2 粒子位置变异操作

多目标粒子群算法与粒子群算法一样，在运行的早期收敛速度较快，但在后期容易陷入局部最优，出现“早熟收敛”现象。算法早期应保持种群多样性，增强算法的全局搜索能力；后期应减弱种群多样性，保证局部搜索能力。为此，本文在寻优过程中采用了递减变异因子执行变异操作，变异概率μ由Sigmoid函数决定，随着迭代次数的增加变异概率μ逐渐减小。

2.3 混合NSGA II-MOPSO算法介绍

NSGA II算法与MOPSO算法的信息共享机制是不同的，NSGA II算法采用遗传算子传递信息；MOPSO算法使用极值GBEST来引导其他粒子，粒子通过更新速度和惯性权重来搜索空间。为了充分利用2种算法的优势，种群在经过随机初始化、非支配排序后，将整个种群分成两半。Pareto等级较好的上半部分种群利用NSGA II算法搜索能力强的特点探索可行域中可能的Pareto解集，并寻找出非支配解储存在外部档案F1中；为避免粒子跟随较高等级GBEST而造成“早熟收敛”，较差的下半部分种群采用MOPSO算法，使Pareto等级较低的粒子收敛到Pareto前沿。2种算法的相互融合使得算法能够更加快速准确地寻找出多目标问题的Pareto最优解集。算法主要流程如下：

步骤1：确定NSGA II算法的相关参数，如种群规模、最大迭代次数、交叉百分比、突变百分比、突变率等。

步骤2：确定MOPSO算法的相关参数，存储库规模、惯性权重因子、个体学习因子和全局学习因子、每个维度的网格数、变异率等。

步骤3：根据预设的变量最大值和最小值对种群进行随机初始化。

步骤4：根据运行成本模型和SO2质量浓度预测模型计算出的初始种群个体适应度进行非支配排序，将种群划分成不同Pareto等级的集合，并根据拥挤距离对同等级集合内部进行排序。

步骤5：将划分好后的种群分为两部分，较好的上半部分种群采用NSGA II算法，较差的下半部分种群采用MOPSO算法。

步骤6：开始NSGA II算法。

1）对上半部分种群执行交叉变异操作，产生子代种群Qt，将父代种群Pt、子代种群Qt合并。

2）将合并后的种群执行快速非支配排序并计算其拥挤距离。根据Pareto等级和拥挤距离对种群排序，列入父代种群Pt+1中。

3）将Pareto等级为1的非支配解储存在外部档案F1中。

步骤7：开始MOPSO算法。

1)根据个体极值选取原则更新个体极值PBEST。

2)将目标空间根据网格划分，记录迄今为止粒子所探索过的位置坐标，使用这些坐标系定位粒子，并采用自适应网格法确定全局极值GBEST。

3)使用式(9)更新每个粒子的速度和位置：

式中：ω(i)为线性调整惯性权重因子；c1为个人学习系数；c2为全局学习系数；K为最大迭代次数；i为当前迭代次数；ωmax、ωmin分别为初始（最大）惯性权重和终止（最小）惯性权重。

4）对粒子的位置执行变异操作。

5）计算种群内每个粒子的适应度并更新外部存储库。

步骤8：将外部档案F1和外部储存库结合，通过快速非支配排序和拥挤距离计算对新种群排序，并将非支配解储存在F1中。

步骤9：判断是否满足终止标准，是则结束迭代，输出结果，否则转步骤5。

步骤10：迭代结束后将外部档案F1数据导出，即得出该问题的Pareto最优解集。

3 仿真研究

3.1 研究对象

本文混合NSGA II-MOPSO算法参数设置见表1。

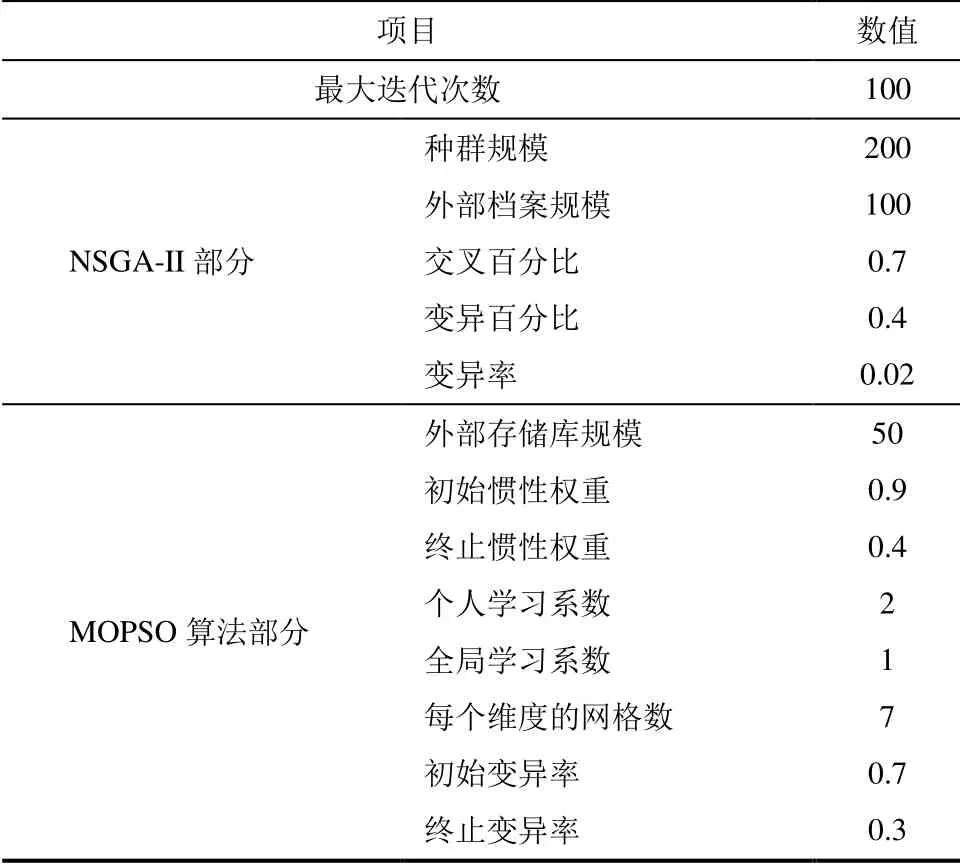
表1 混合NSGA II-MOPSO算法参数设置 Tab.1 Parameter settings for the hybrid NSGA II-MOPSO algorithm

以某660 MW燃煤机组脱硫系统历史数据为研究对象，该系统主要设备有增压风机2台（1主1备）、浆液循环泵3台（A、B、C）、氧化风机3台（2主1备），其中3台浆液循环泵均为功率800 kW的工频泵；石灰石单价选取近期市场平均价格，价格为250元/t。该机组长期承担调峰任务，负荷在50%～100%范围内变动。

3.2 结果与讨论

本文采用混合NSGA II-MOPSO算法作为优化算法，寻找脱硫系统的最佳运行策略，并利用本文算法、MOPSO算法与NSGA II算法进行对比实验。经过50次迭代后，外部档案产生100个Pareto最优解。

根据国家环保标准，燃煤机组出口SO2质量浓度要低于35 mg/m3，为避免因负荷、煤质等的变化、设备控制策略的不稳定性以及运行故障等其他不可控因素造成的污染物出口质量浓度大范围波动甚至超标，在优化过程中将SO2质量浓度限值在国家标准上进一步控制，设为25 mg/m3。根据前文分析，出口污染物质量浓度越低，则脱硫系统运行成本越高；反之，出口污染物质量浓度越高，即在可行域范围之内越接近污染物排放质量浓度限值，则脱硫系统运行成本越小，由此可得，通过优化算法求得的最优解应在污染物排放质量浓度限值附近。

为验证混合优化模型在不同工况下的优化效果，本文选取燃煤机组48 h内的4个典型工况历史数据（表2）。将工况数据输入混合优化模型，可以得到不同工况下的Pareto最优解集。将3种算法得到的Pareto前沿对比，图4为NSGA II、MOPSO和混合NSGA II-MOPSO算法在工况4条件下得到的Pareto前沿。

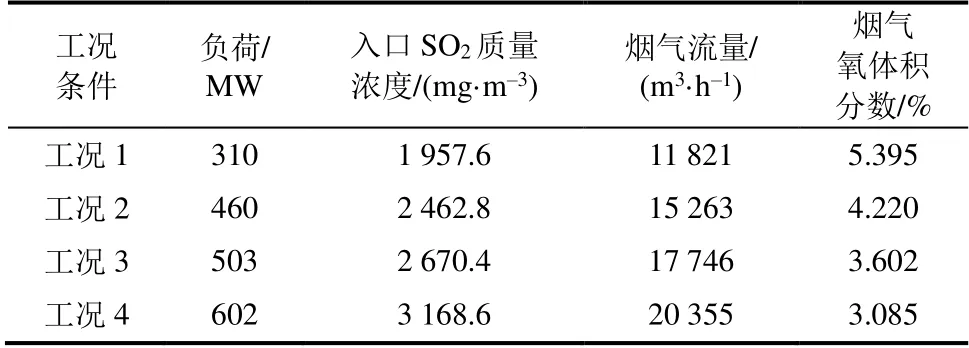
表2 典型工况条件数据 Tab.2 Data of typical operating conditions

由图4可见，运行成本与环境成本总体呈负相关性。混合NSGA II-MOPSO算法得到的Pareto前沿相比于其他算法更加光滑均匀，在可行域内具有更佳的扩散性。根据Pareto最优解集在出口污染物质量浓度限值附近得到的最佳运行成本以及对应的最佳可变操纵量参数，优化前后脱硫系统度电运行成本对比见表3；优化前后各工况条件下WFGD主要操纵量见表4。

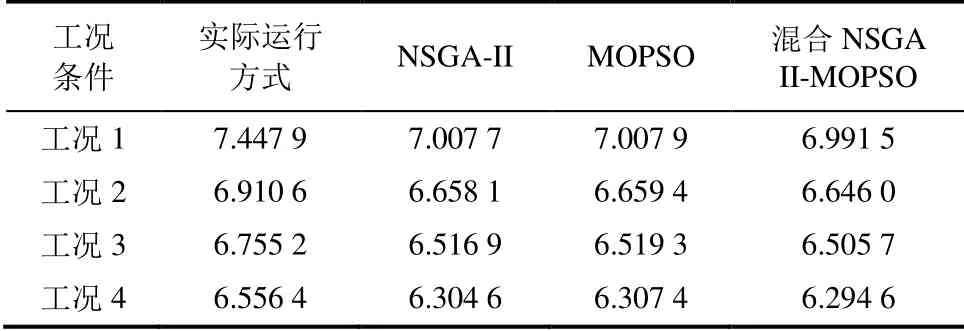
表3 优化前后脱硫系统度电运行成本对比 单位：×10-3元/(kW·h) Tab.3 Comparison of cost per kW·h of the desulfurization system before and after optimization

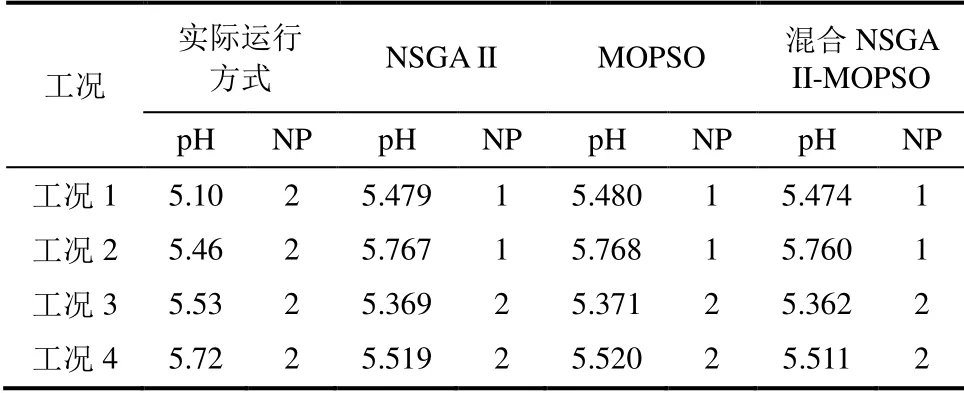
表4 优化前后各工况条件下WFGD主要操纵量 Tab.4 Main operation amount of the WFGD before and after optmization under various operating conditions

由表3可知，相比于实际运行方式，优化后运行策略的度电成本有明显下降。不同算法优化效果有所不同，NSGA II算法和MOPSO算法的优化结果十分接近，混合算法相较于其他2种算法度电成本得到更进一步的优化，4个工况条件下混合算法得到的度电成本相较于其他算法分别下降了0.23%、0.18%、0.17%、0.16%。混合算法优化度电成本与实际运行度电成本相比，工况1、工况2时降低比例较大，分别达到了9.38%和6.01%，工 况3、工况4时成本下降幅度有所减小，分别达到3.69%和3.99%。这是由于循环泵在运行成本中占比较大，当循环泵台数发生变化时优化效果较为明显。使用该优化模型能够有效降低脱硫系统运行成本，而混合NSGA II-MOPSO算法得到度电成本更低，能够使机组以更经济的方式运行。

由表4可知，优化后最佳可变操纵量参数与 实际可变操纵量参数相比有明显调整，工况3、工况4时在浆液循环泵台数不变的情况下，pH值得到明显降低。工况1、工况2时浆液循环泵少开启1台，而pH值只是稍微增加，使得优化后的总度电成本降低。该优化模型为脱硫系统提供了物耗能耗较低的可变操纵量设定值，从而实现对烟气污染物脱除低成本高效率的控制。

4 结 论

1）本文针对运行成本和环境成本相互制约的问题，建立了一种燃煤机组脱硫系统混合优化模型实现对运行策略的优化。该模型以运行成本和出口污染物质量浓度为优化目标，采用混合NSGA IIMOPSO算法得到Pareto最优解集，在出口污染物质量浓度限值附近，得到脱硫系统最佳运行策略。

2）选取脱硫系统历史数据中4个典型工况验证该模型优化效果，结果显示，使用该优化模型对脱硫系统进行优化能有效降低系统运行成本。通过对可变操纵量参数的优化，可以保证脱硫系统在出口污染物质量浓度不超限的情况下运行成本最低，在实际生产中可为运行人员提供指导，实现系统经济高效的运行。