圆盘通孔叶轮的能量转换特性

王桃,向茹*,严敬,周敏

(1. 西华大学能源与动力工程学院，四川 成都 610039; 2. 流体及动力机械教育部重点实验室(西华大学)，四川 成都 610039)

为适应一些特殊的工作环境，工业中常要求某种泵类产品的叶轮具有特殊的结构形式，如叶轮内的流道采用径向布置，水流流过叶轮的相对运动轨迹与叶轮半径重合.带有径向孔的圆盘通孔叶轮就有类似的结构特点[1-3].

目前常规离心泵叶轮研究广泛，而国内外关于具有圆盘通孔叶轮的超低比转数离心泵的研究鲜见文献报道.由于结构不同，常规离心泵的设计理论无法完全应用于圆盘通孔泵.目前国内外学者主要针对圆盘通孔泵径向孔布置形式及工作性能等方面进行研究.王者文等[4]设计了1种圆盘通孔叶轮，研究表明，带有该特殊叶轮的泵水力效率明显提高，同时证明了圆盘通孔叶轮可用于超低比转数离心泵.郑辉等[5]设计了具有3种不同形式的圆盘通孔叶轮的泵,并基于多工况对其进行数值计算.赖喜德等[6]提出了适合圆盘通孔叶轮流道设计及优化方法，并预测了泵性能.张飞等[7]针对某抽水蓄能电站首台机组调试阶段机组推力轴承圆盘通孔泵不能建压的问题及其可能产生的原因，预测了圆盘通孔泵在中高转速下存在的压力和流量不稳定区.雷霆等[8]评估了银盘水电站推力轴承支撑性能对机组运行的稳定性以及验证圆盘通孔泵外循环技术在设计工况下的冷却效果,证明了圆盘通孔泵外循环系统能够在设计工况点附近工作且冷却效果较好.卢珍等[9]研究了集油槽喉部面积对圆盘通孔泵性能影响，为优化圆盘通孔泵性能提供了一定依据.

综上所述，对圆盘通孔泵的研究主要集中在圆盘通孔泵泵孔设计及其冷却循环性能方面，而关于圆盘通孔泵叶轮做功原理及外特性分析的研究较少.文中以定量的数学分析为基础，通过对圆盘通孔叶轮的连续介质运动规律及受力分析，推导圆盘通孔叶轮的能量转换特性及运行性能，从而为分析圆盘通孔叶轮内的流动及叶轮做功特性提供一定的理论依据.

1 圆盘通孔叶轮对水流的做功原理

图1为某一典型的圆盘通孔叶轮，可以看出，该叶轮结构较简单，其流道为由8～16个钻头形成的等截面圆孔，这些均匀分布的孔沿径向直通叶轮出口.水流由叶轮入口分别进入各通孔内，在旋转叶轮中获得能量后再沿径向方向流出叶轮.

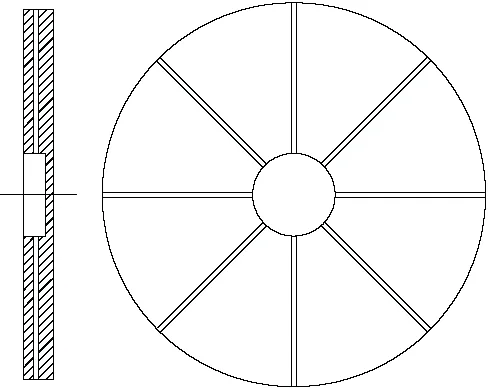
图1 圆盘通孔叶轮结构

在工作过程中，泵通过叶轮对水流做功，将原动机的机械能转化为流体的机械能.一般而言，要求旋转叶轮的叶片两侧必须有阻止叶轮旋转的压力差，原动机克服这一压力差维持叶轮正向旋转从而对水流做功.

在常见的离心叶轮中，叶轮旋转时，离心叶轮内两相邻叶片之间的宽敞流道内有条件形成一特殊相对流动，即轴向旋涡.因此，叶轮内水流的相对运动被看作2个特殊相对流动的叠加，即均匀流与轴向旋涡流.在叶片背面，这2个相对流动的流向一致，而在工作面则相反.因此，在同一半径上，水流在叶片背面的相对速度将大于工作面的对应值，相对运动伯努利方程决定了流体压力与其相对速度负相关，导致叶片工作面压力较大，这就形成了叶片两侧的压力差[10-13].但是，文献[2-3]证明，在圆盘通孔泵的叶轮狭小流道中没有产生轴向旋涡的条件，这是因为在这一狭小管状流道中，黏性力将阻止水流双向流动.通过对沿径向流道的流体质点的受力分析，可定量证明叶轮作用于水质点而产生质点哥氏加速度的外力所做的功是水质点机械能增加的原因，且叶轮做功等于水质点机械能的增量.显然，圆盘通孔叶轮对水流的做功原理与一般叶片泵不同.

2 径向运动孤立质点功能原理分析

图2为一圆盘通孔叶轮绕其中心点O以均匀角速度ω逆时针旋转示意图.

图2 圆盘通孔叶轮中的流体质点加速度

固态质点的绝对加速度为其相对加速度ar、牵连加速度ae和哥氏加速度ak三者的矢量和.在任意时刻对单位质量的流体质点，根据牛顿第二定律有

ar+ae+ak=F，

(1)

式中：F为固态壁面对固态质点的作用力.

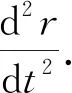
因此，将式(1)等号两端的矢量投影到相对径向坐标轴r上[14]，式(1)则变为

(2)

该微分方程的通解[15]为

r=c1eωt+c2e-ωt，

(3)

且有

(4)

将c1，c2代回式(3)和式(4)后，得到质点的位移及相对速度随时间t的变化规律为

(5)

(6)

(7)

(8)

在任意时刻，质点的哥氏加速度大小为2ωvr,其方向与质点所在半径垂直且与叶轮旋转方向一致.这一加速度显然是运动叶轮对质点施加的同向压力产生的.质点在单位时间内的位移可以分解为径向和圆周方向2个相互垂直的分量.由于径向分量与质点所受叶轮压力垂直，质点所受外力在此方向不做功.此外，如果此时质点在相对坐标轴上距中心距离为r，质点在圆周方向上位移为rω，由于质点的哥氏加速度与位移方向一致，叶轮对单位质量质点做功功率为2ωvrrω.进一步可得到从初始时刻到时刻T叶轮对质点做功为

(9)

式(8)和式(9)分别表示在同一时间段内质点机械能的增加量和叶轮通过产生质点哥氏加速度的作用力对质点所做的功，它们有完全不同的物理内容，导出方法也不相同，但结果表达式完全一样.这就从理论上定量证明了在圆盘通孔叶轮中，孤立固态质点机械能的增加与质点在叶轮中的哥氏加速度相关，而且这一增量正是叶轮作用于质点上产生质点哥氏加速度的外力对固体质点做功的结果.实际上，这一现象是具有普遍意义的动能定理在圆盘通孔叶轮中的体现.

3 径向运动连续介质机械能增量分析

上述分析与计算揭示了圆盘通孔泵径向流道中运动质点的机械能增量与质点所受哥氏力做功之间的关系，提供了圆盘通孔泵不同于离心泵叶轮中运动质点的能量转换原理.但是，由此得到的结论并不适合圆盘通孔泵中的连续介质，原因在于，上述研究对象为圆孔孔道中运动的孤立固态质点，而泵处理的是连续介质.虽然上述的分析及结论并不能直接用于连续介质，但为推导圆盘通孔泵的基本方程提供了借鉴与启发.下面将利用能量转换原理，推导连续介质在流通圆盘通孔泵后机械能增长的表达式，并分析其成因.

定义叶轮产生的动扬程Hv为单位重量的水通过叶轮后动能的增量.在圆孔流道中任一点处，水流的相对速度矢量与半径重合，牵连速度矢量则与半径正交，它们按矢量合成原则确定的绝对速度将与2个其他速度构成一直角速度三角形，如图3所示.

图3 流动质点的直角速度三角形

泵的理论扬程HT为泵的势扬程Hp和动扬程Hv之和，即

(10)

式(10)即以运动学物理量表示动力学物理量的圆盘通孔泵的理论扬程表达式，这一表达式也可称为圆盘通孔泵的基本方程.

圆盘通孔泵的理论扬程表达式(10)与离心泵的基本方程在形式上完全一致.离心泵的基本方程为

HT=(u2vu2-u0vu0)/g,

(11)

式中：vu2，vu0分别为离心泵叶片出口与入口处绝对速度在圆周方向的投影.

深入分析式(10)，可以得到一些有意义的结果.在圆盘通孔泵中，在圆孔流道出口与进口处，由于速度三角形都是直角三角形，绝对速度的圆周投影与牵连速度重合，因而vu2=u2,vu0=u0,于是圆盘通孔泵的基本方程可以写成式(10),也可以写为式(11).这里应指出，尽管离心叶轮和圆盘通孔叶轮的基本方程在形式上一样，但2种叶轮对水流做功的原理并不相同.在现有文献中，离心泵的基本方程都以质点系的动量矩定理导出，2种叶轮产生的理论扬程的推导原理与方法也不相同.

在叶轮结构与转速一定时，由于叶片进出口处离心泵的绝对速度的圆周分量与通过流量有关，由式(11)可知，叶轮产生的理论扬程将随泵的流量变化而变化[16].但是，通过圆盘通孔泵圆孔流道流量的变化只改变进出口三角形的高，并不改变绝对速度的圆周分量，因而圆盘通孔泵产生的理论扬程不随流量变化而变化.

水流在叶轮中的水力损失与叶轮中的相对速度正相关，因而也与叶轮流量正相关，泵的扬程将随流量增大缓慢下降.圆盘通孔泵产生的理论扬程HT和H随流量变化的特性曲线应当是一条水平线和一条缓慢下降的曲线，如图4所示.

图4 圆盘通孔泵的扬程-流量曲线

圆盘通孔泵这种完全不同于离心泵的特性曲线形态已被试验所证实.适当增大叶轮圆孔直径有利于降低水流相对速度和水力损失，扬程曲线会更平坦一点.在一些生产线上，有时要求在恒扬程下改变系统流量.圆盘通孔泵的这一优秀性能是离心泵所不具备的.

离心叶轮两叶片之间的流道是扩散的，而圆盘通孔泵的流道为等截面圆形通道，因而避免了泵中的扩散损失.此外，在流道断面面积一定的条件下，圆形断面有更小的湿周和摩擦面积，这就减少了沿程水力损失.以上2个原因决定了圆盘通孔泵有更高的水力效率，这一点已被试验所证实.

质点机械能的增加是外力对质点做功的结果，与孤立质点相类似，连续介质机械能的增加也是产生水流哥氏加速度的叶轮作用力做功的结果.圆盘通孔泵的圆孔流道内各水质点的哥氏加速度实际是一沿圆周方向常量2ωvr，微柱体受到叶轮作用的相同方向的外力应为微柱水体质量与哥氏加速度的乘积2ωvrρSdr.单位时间内，水体在圆周方向位移为ωr.如前文所述，尽管水质点的径向位移与产生质点哥氏加速度的外力垂直，外力不做功，但是，由于水体的受力方向与水质点圆周位移方向一致，在单位时间内，叶轮对微水体做功应为两者之积，即2ωvrρSdrωr=2ρSω2rvrdr.从孔道入口到出口对上式进行积分，有

(12)

4 结 论

以相关力学定律为依据，通过数学分析以理论方法证明了圆盘通孔泵不同于一般叶片泵的性能特征，得到结论如下：

1) 在圆盘通孔泵中，流体机械能的增量来源于产生流体哥氏加速度的叶轮作用力对流体所做的功，而不同于叶片泵叶轮克服叶片两侧压力差而完成能量转换.

2) 圆盘通孔泵转速一定时，叶轮产生的理论扬程不随流量变化而变化.

3) 叶轮直径和转速都相同时，圆盘通孔叶轮将产生更高的扬程.