SU(3)协变手征有效理论与八重态重子质量修正

刘 舟, 杨继锋

（华东师范大学 物理与电子科学学院, 上海 200241）

0 引 言

尽管量子色动力学(Quantum Chromodynamics, QCD)被公认为是描述强相互作用的基本理论,但夸克禁闭使人们很难直接使用该理论进行中低能区的解析计算. 为此, 人们发展了数值的格点QCD 来进行非微扰计算[1]. 但目前在数值计算时需采用大于物理值的夸克质量, 计算的结果需要进一步外推至物理值区域, 因此仍需系统自洽地解析结果进行比对. 为了可以解析地计算中低能强子物理过程, 有效场理论(Effective Field Theory, EFT)被引入并应用于QCD 的中低能区. 要构造手征有效拉氏量, 需要借助QCD 的手征对称性及存在的其他对称性, 拉氏量的基本自由度被各种强子取代. 这样的场理论被称为手征微扰理论(Chiral Perturbation Theory, ChPT). ChPT 作为QCD 的低能有效场论, 最初被应用于介子系统, 并取得了巨大成功[2-4].

但当这个理论被运用到重子系统时, 由于重子质量标度很大, 会破坏手征幂律规则. 为此, 学术界尝试了多种方法来恢复手征幂律规则, 比如重重子展开[5]; 但随后发现该展开在某些情况下不能给出收敛的结果. 之后, 人们尝试在协变框架下引进了更多复杂的正规化来保证手征幂律规则, 比如红外正规化[6]和扩展的在壳减除(Extended On-Mass Shell, EOMS)[7]方案. 红外正规化直接处理圈图积分, 将圈图积分分为红外奇异部分与正规部分; 该方案将符合手征幂律规则的项保留在红外奇异部分,其余的项都归为正规部分; 但在该方案下, 一些形式上压低的修正项得不到保留. EOMS 方案在积分前对外动量做泰勒展开, 然后进行费曼积分, 计算出不满足手征幂律规则的贡献并减除; 该方案虽然能够使所得的结果符合手征幂律规则, 但同样会造成对结果的过度减除. 本文小组之前的研究: 直接在协变形式下, 细致分析单核子结构、矢量介子, 以及核子-核子散射一圈图、两圈图后, 发现破坏手征幂律规则的项都是定域的, 可直接减除, 从而指向一个协变框架下的简单解决方案—扩展的极小减除( EMS )[8-12]方案. 相较于其他处理方式,方案更为简洁, 并且不引入任何新的理论操作或额外的修改, 既保持了圈图的解析性质, 也不会造成过度减除. 在此基础上, 本文在协变框架下, 计算了虚的八重态、十重态重子对八重态重子质量的一圈图修正, 探讨了方案在SU(3)系统的适用性.

本文后续的主要内容为: 第1 章介绍拉氏量及相应的理论框架; 第2 章计算费曼图并分析其解析结构; 第3 章是结论.

1 理论框架

本文采用的手征微扰理论框架下赝标量介子与八重态、十重态重子系统的最低阶协变有效拉氏量[13-15]为

m是夸克质量矩阵, 记作m=diag(mu,md,ms),mu、md和ms分别为上夸克、下夸克以及奇异夸克的质量, 在本文的计算中, 只考虑质量较大的奇异夸克的贡献; 用 3×3 的幺正矩阵φ描述赝标量介子,将重子八重态整合在无迹的 3×3 矩阵B中, 即

从拉氏量可以得出协变的相互作用顶角与传播子.

2 费曼图计算与分析

计算八重态介子质量与八重态重子质量的树图可以近似得到

公式(14)中的αB,B=N,Σ,Λ,Ξ,对应有

由于忽略了上夸克、下夸克的质量, 所以在树图近似下 π 介子质量为0. 本文的计算暂不考虑 π 介子的贡献.

2.1 八重态重子的贡献

本小节主要讨论八重态重子对八重态重子质量的一圈图修正. 费曼图见图1.

图1 八重态重子对八重态重子质量修正一圈图Fig. 1 One-loop correction to octet baryon masses by octet baryons

图1 中, 实线为八重态重子线, 虚线为赝标量介子线, 实心三角形和实心菱形表示源自拉氏量L1的相互作用顶角, 实心圆是源自拉氏量L0的介子与八重态重子相互作用三顶角. 图1(a)—图1(e)直接给出了重子质量的部分修正, 图1(f)、图1(g)考虑的是波函数重整化对重子质量的贡献. 更为详细的圈图积分结果可参考附录A, 结果中出现的符号有定义(φ=K,η;B=N,Σ,Λ,Ξ)

图1(a)、图1(b)结构简单, 费曼振幅经过维数正规化和参数积分后, 结果分别为

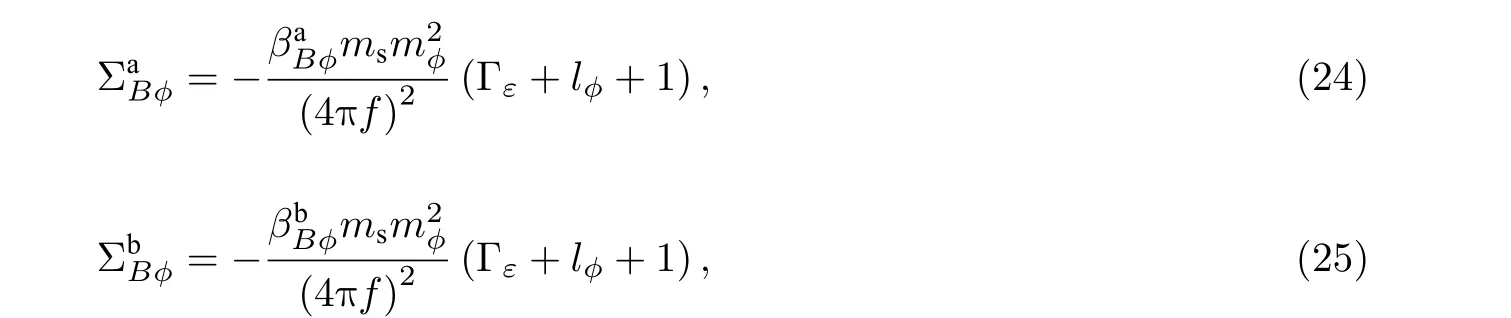
其中,µ为重整化能量标度;是对应不同重子和介子的系数, 详见表1 和表2.

表1 系数Tab. 1 Coefficients of

表1 系数Tab. 1 Coefficients of

βBa φ K η N Σ Λ Ξ 2(b1 +2b2)2(b1 +b2)10(b1 +b2)/3 2(2b1 +b2)8b2/3 0 16(b1 +b2)/9 8b1/3

表2 系数Tab. 2 Coefficients of β

表2 系数Tab. 2 Coefficients of β

βBb φ K η N Σ 8σ 8σ/3 Λ Ξ

图1(c)、图1(d)是考虑虚的八重态重子对重子质量贡献的自能图, 费曼振幅分别为

表4 系数Tab. 4 Coefficients of

表4 系数Tab. 4 Coefficients of

βBd φ K η N −2(D+3F)2(b1 +b2)/9−(D −3F)2b2/3 Σ Λ−2(D+F)2b1 −2(D −F)2b2−2(D −3F)2b1/3 −2(D+3F)2b2/3 0−8D2(b1 +b2)/9 Ξ−2(D −3F)2(b1 +b2)/9−(D+3F)2b1/3

经过积分, 得到的解析结果分别是

结果仍可归为3 类, 图1(e)与图1(d)圈图结构相同.

对图1(c)—图1 (e), 采用 E MS 方案, 减除费曼振幅中的手征发散项及破坏手征幂律规则的定域项, 得到的结果分别是

减除后的结果中除了满足手征幂律规则的定域项, 还包括相对论修正项, 即δBφ对应部分, 在ρφ →∞的极限下, 该部分趋于0.

减除后的结果为

此质量公式中, 除了手征贡献, 本文还保留了形式上压低的修正项.

2.2 十重态重子的贡献

本小节讨论虚的十重态重子对八重态重子质量的一圈图修正. 费曼图见图2.

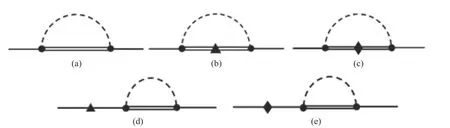
图2 十重态重子对八重态重子质量修正一圈图Fig. 2 One-loop correction to octet baryon masses by decuplet baryons

图2 中, 双实线代表十重态重子线, 实心圆是源自拉氏量L0的介子与八重态、十重态重子相互作用三顶角. 图2(a)—图2 (c)直接给出了重子质量的部分修正, 图2(d)、图2(e)考虑了波函数重整化对八重态重子质量的贡献. 结果中出现的符号定义为(T=)

表5 系数Tab. 5 Coefficients of

表5 系数Tab. 5 Coefficients of

γ˜BφKη N C2/2 0 Σ Λ 5C2/3 C2 C2/2 0 Ξ 3C2/2 C2/2

表6 系数Tab. 6 Coefficients of

表6 系数Tab. 6 Coefficients of

β˜Bb φ K η N cC2/3 0 Σ Λ 4cC2/9 4cC2/3 cC2/3 0 Ξ 7cC2/3 2cC2/3

图2(a)的积分结果是

在2.3 节, 将对以上圈图结果进行讨论和分析.

2.3 计算结果总结及比较

结合树图近似及八重态、十重态重子的贡献, 八重态重子的质量为

其中, 系数ωB、ξB详见附录C. 以上结果与文献[11]在重重子手征微扰理论下的计算结果相符.

3 结 论

本文在SU(3)协变手征有效理论框架下, 主要计算了虚的八重态、十重态重子对八重态重子质量的一圈图修正; 发现结果中破坏手征幂律规则的项都是定域的, 可以通过定域抵消项减除, 这与我们在核子系统得到的结论一致, EMS 方案仍然可行. 尤其是在考虑十重态重子的贡献时, 出现了一些看似“反常”的结果, 但是通过进一步展开这些“反常”项, 发现它们仍属于有限的相对论修正项. 除了手征贡献, 本文的计算还保留了形式上压低的修正项, 这些项在非手征极限下并不为0, 它们对精确计算重子质量有意义, 并且对解析外推有重要贡献. 接下来的工作中, 将进一步考虑十重态重子质量修正,并关注除质量以外, 诸如磁矩这一类重要的物理量, 更深入地分析SU(3)系统中圈图的解析结构及探索方案的适用性.

附录B Xn

附录C 系数 ωB 、ξB