小波包变换和数学形态滤波器在局部放电信号去噪中的应用
王珊珊,孟 阳,何晓会,谢 明,赵忠锋
(1.哈尔滨电站科技开发有限公司,哈尔滨 150046;2.国网黑龙江省电力有限公司物资公司,哈尔滨 150001;3.国网黑龙江省电力有限公司电力科学研究院,哈尔滨 150030)
0 引 言
局部放电会导致变压器绝缘劣化,影响变压器的使用寿命,甚至危及电力系统的安全运行。为实时监测变压器的绝缘状态,需要在设备运维过程中,对变压器局部放电进行在线监测,以及时发现设备绝缘缺陷,并及时检修,防止事故发生,保证电力系统的安全运行。
变压器在发生局部放电时,监测信号中含有各种复杂的噪声干扰。为提取准确的局部放电信号,必须抑制或者消除这些干扰信号。变压器局部放电监测中信号去噪技术按原理分为干扰源去噪、干扰途径去噪和信号后处理去噪等,目前比较常用的去噪技术有自适应形态滤波法、经验模态分解法、快速傅里叶变换(fast fourier transform,FFT)阈值滤波法和小波阈值法等[1-3]。但是,这些方法或计算量大,或阈值选择难度大,影响去噪效果。
因此,设计一种基于小波包和数学形态学原理的去噪方法,采用数学形态学原理提取局部放电形态特征,并编制相应的程序,最后进行理论分析和仿真验证。
1 小波包与数学形态滤波器变换融合去噪
1.1 数学形态学运算
数学形态学的基本运算有4个:膨胀、腐蚀、开运算、闭运算[4-6]。
设待处理信号f(n)是一维离散函数,定义域为Df={0,1,2,…,N};g(n)为一维结构元素序列,定义域为Dg={0,1,2,…,P};其中N∈Z,P∈Z,N≥P。则f(n)关于g(n)的腐蚀(fΘg)(n)和膨胀(f⊕g)(n)分别为
(fΘg)(n)=min[f(n+x)-g(x)]
(n+x)∈Df且x∈Dg
(1)
(f⊕g)(n)=max[f(n-x)+g(x)]
(n-x)∈Df且x∈Dg
(2)
由式(1)、式(2)可得,f(n)关于g(n)的开运算f∘g和闭运算f·g分别为
f∘g=fΘg⊕g
(3)
f·g=f⊕gΘg
(4)
数学形态学通过移动结构元素提取信号来进行特征分析。实际应用中,一般采用开运算和闭运算的组合来构建形态学滤波器的算法。
1.2 去噪流程
采用小波包变换融合数学形态学进行局部放电信号去噪,因为采用阈值法,小波包变换系数值可能与局部放电信号中的部分小波包变换系数值近似或低于阈值,而被误认为噪声过滤掉[7]。为了使原始局部放电信号有效保留,先选择合适的小波函数进行小波分解,并提取小波包分解系数,应用广义形态滤波器进行滤波,然后设置阈值,乘以系数,得到相对较小的新的阈值,以最大限度保留原始信号,最后重构小波包分解系数,得到消噪后的信号,小波包变换与数学形态滤波器融合去噪流程如图1所示。
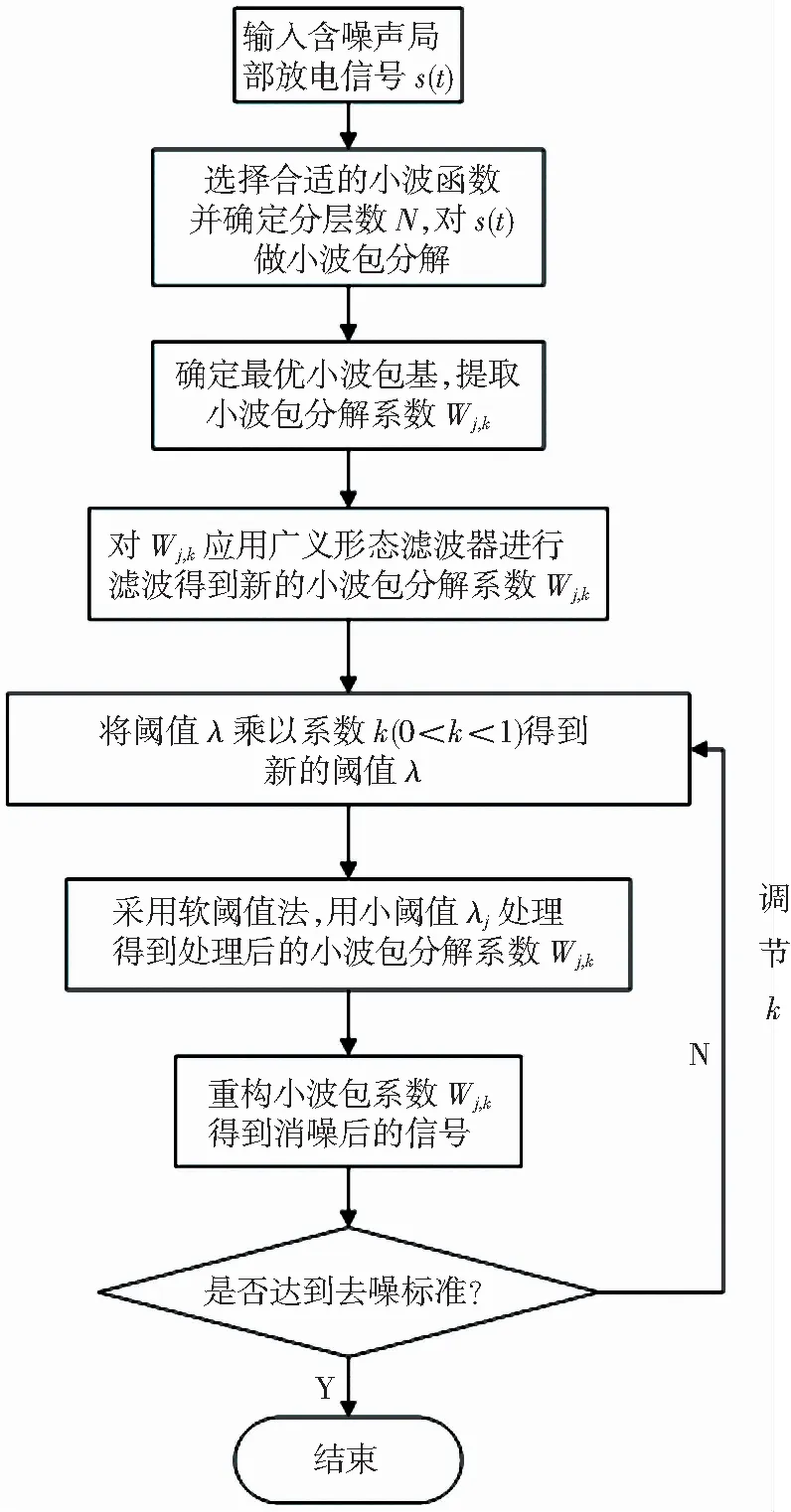
图1 小波包变换与数学形态滤波器融合去噪流程图Fig.1 Flow chart of wavelet packet transform and mathematical morphological filter fusion denoising
1.3 评价参数
为了验证小波包变换与数学形态滤波器融合去噪方法的有效性,引入均方误差eMES,来表示波形的失真率,并对波形相关性进行定量描述,引入波形相关性系数kNCC,分别定义如下。
(5)
(6)
式中:x(n)为原始参考信号;x′(n)为去噪后的信号;M为信号长度。
2 仿真去噪效果
常用的局部放电去噪方法有EMD多分辨率方法、小波阈值法等。EMD多分辨率方法是利用EMD分解对含有噪声的局部放电信号进行剔除处理,通过对固有模态函数(intrinsic mode function,IMF)分量进行阈值处理,重构IMF分量,从而得到高信噪比的数据形态[8-9]。小波阈值法基于小波分析方法,先对带噪信号进行小波分解变换,得到分解系数,再设置一个临界阈值,将局部放电信号进行分解和阈值处理,最后进行小波重构,重构原始放电信号。
采用EMD方法、小波阈值法和所提方法分别对混有噪声的局部放电信号进行去噪处理,得到的局部放电信号放电效果如图2所示。
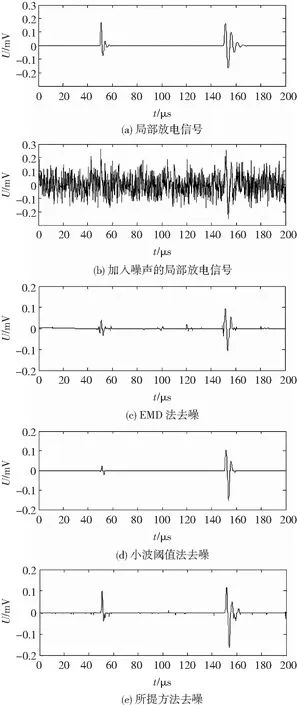
图2 局部放电信号去噪结果Fig.2 Partial discharge signal denoising result
由图2可以看出,图2(e)所示小波包与广义形态滤波器融合法去噪方法的局部放电信号波形与图2(a)所示的原局部放电信号仿真波形最为接近,因此所提方法的去噪效果优于EMD法和小波阈值法。
将原始参考信号和去噪后的信号代入式(3)、式(4),得到均方误差eMES和波形相关性系数kNCC,结果见表1。
由表1可见,所提方法的均方误差小于EMD法和小波阈值法,波形相关性系数大于EMD法和小波阈值法,表明该方法波形失真率最低,去噪后的波形最接近原波形。
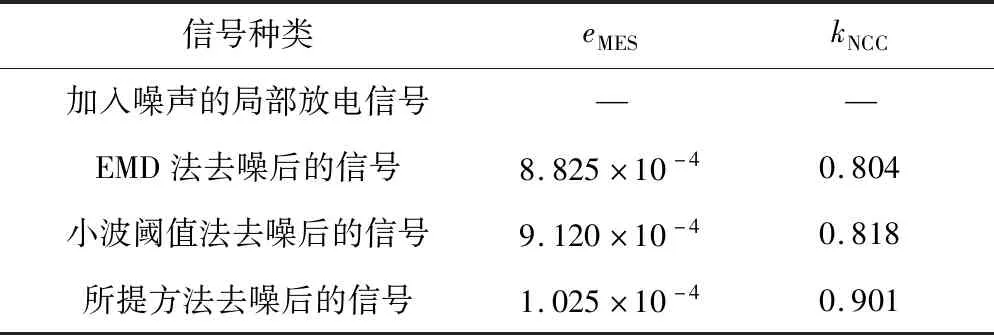
表1 评价参数Table 1 Evaluation parameter
3 实测信号去噪效果
通过对某电厂的主变局部放电信号进行现场实测,验证所提方法的去噪效果。图3为某电厂现场实际测量的主变局部放电信号,图4为采用小波包与广义形态滤波器融合法去噪后的局部放电信号。
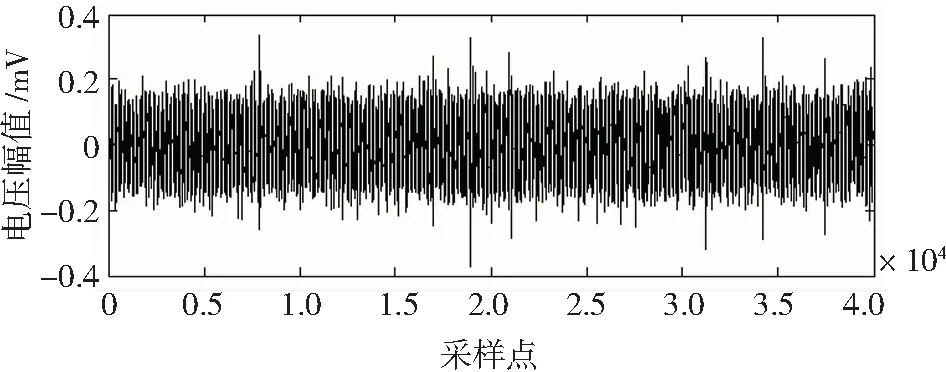
图3 实测局部放电信号Fig.3 Measured partial discharge signal
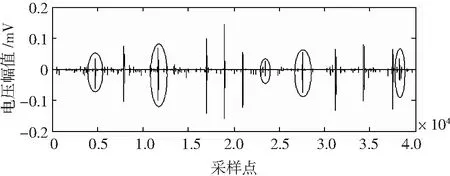
图4 小波包与广义形态滤波器融合法去噪后的局部放电信号Fig.4 Partial discharge signal denoised by wavelet packet and generalized morphological filter
通过图3、图4对比分析,可见采用小波包与广义形态滤波器融合的去噪方法有良好的去噪效果。
4 结 语
分析了小波包变换和广义形态滤波器融合消噪的基本原理,通过仿真分析,对比小波阈值法、EMD方法及所提方法的去噪效果,得出所提方法的去噪效果较好,减小了信号的失真率。
通过现场实测,验证了该方法在现场局部放电信号去噪中的有效性,表明了该方法在局部放电在线监测中具有较好的现场应用前景。

