基于CF与SVM的小样本斜坡地质灾害敏感性评价研究

薛永安，王玉洁，朱婧聪，李昊辰，张明媚

(1.太原理工大学 矿业工程学院，太原 030024；2.山西能源学院 地质与测绘工程系，山西 晋中 030600；3.中国科学院地理科学与资源研究所 中国科学院陆地表层格局与模拟重点实验室，北京 100101)

地质灾害敏感性评价(也称易发性评价)是利用数学语言评估在一定地质环境条件下灾害空间概率的敏感性[1]，评价方法主要分为定性评价与定量评价[2]，目前常用的定量评价模型主要包括：层次分析法[3]、逻辑回归模型[4]、神经网络法[5]、证据权重法[6]、信息量法(information value，I)[7]、确定性系数法(certainty factor，CF)[8]、随机森林(random forest，RF)[9]和支持向量机(support vector machine，SVM)[10]等。然而，采用这些模型存在评价因子分级量化主观性较强，以及评价因子组合权重客观性不足的影响，因此，组合评价模型逐渐成为研究热点[11-12]，如基于CF与SVM的耦合易发性评估模型[8]、信息量与Logistic回归的耦合模型[13]、确定性系数与层次分析法、逻辑回归方法和神经网络多层感知器方法组合的区域滑坡敏感性评价[14]、CF与Logistic回归模型耦合[15]，为敏感性评价模型组合研究提供了丰富的参考。同时有学者采用不同的模型进行对比研究[16]，以及组合与对比同时进行的研究工作，如杨强等[12]采用信息量法、确定性系数法、证据权法分别与逻辑回归组合，对3种组合模型进行对比选取最佳评价模型。这些研究工作，为地质灾害敏感性评价奠定了坚实的基础，也为后续研究提供了丰富的成果参考。

山西省五寨县地质灾害防治“十三五”规划(2016-2020年)表明，2017年全县初步确定地质灾害隐患点53处，隐患类型主要为崩塌和不稳定斜坡两种(以下统称斜坡地质灾害)，直接威胁人口588人，房屋594间，财产603万元，给当地经济发展带来极大影响。开展斜坡地质灾害敏感性评价可以为危险范围预测及重点防治区域区划等方面提供理论依据与技术支撑[15]，也是国土空间规划中城乡公共安全与地质灾害防治规划的主要工作内容之一，对保障五寨县国土空间规划顺利开展、人民群众生命财产安全和社会经济可持续发展具有重要的现实意义。李远远等[8]以CF模型和SVM模型构建了CF-SVM易发性评估模型，CF方法作为SVM分类数据的获取方法，以云南省怒江州泸水县381个地质灾害隐患点进行了CF-SVM与SVM的易发性评价对比研究，结果表明，CF-SVM模型优于SVM模型。然而该文未对比CF模型评价结果，且地质灾害样本数量较多，上述结论对于小样本的区域性斜坡地质灾害敏感性评价是否适用尚未可知，但这些研究工作的展开，为区域斜坡地质灾害敏感性评价工作提供了基础参考。

历史编录地质灾害数据是目前敏感性评价中主要采用的数据源，但该数据集与具体年份的基础地理数据之间存在失相关，而与基础地理数据保持相近时相的地质灾害发育数量一般较历史编录数据集要少。针对小样本情况下地质灾害敏感性评价模型的适用性及成果的可靠性问题，本文选择高程、坡度、坡向、地势起伏度、地质构造、地层岩组、道路工程扰动、河流水系和表征植被覆盖的归一化植被指数(normalized difference vegetation index，NDVI)为斜坡地质灾害敏感性评价因子，选择基于统计思想的CF模型和基于机器学习的SVM模型作为评价模型，同时进行模型组合(CF-SVM模型)，分别以CF模型、SVM模型和CF-SVM模型开展了山西省五寨县斜坡地质灾害敏感性评价对比，并以受试者特征曲线(receiver operating characteristic，ROC)下面积(area under the ROC curve，AUC)检验了模型精度，综合频率比、AUC值和敏感性分区图对比得到最佳评价模型及评价结果，最后采用I模型与SVM模型的组合(I-SVM模型)结果进行了对比分析，以期为小样本情况下地质灾害敏感性评价提供更可靠的模型选择参考与最佳结果，同时为五寨县城乡公共安全与地质灾害防治规划提供科学支撑。

1 研究区概况及数据源

1.1 研究区概况

五寨县(图1)位于山西省西北部黄土高原丘陵区，管涔山北麓，地理范围：E111°28′～E113°00′，N38°44′～N39°17′，总面积1 391 km2.

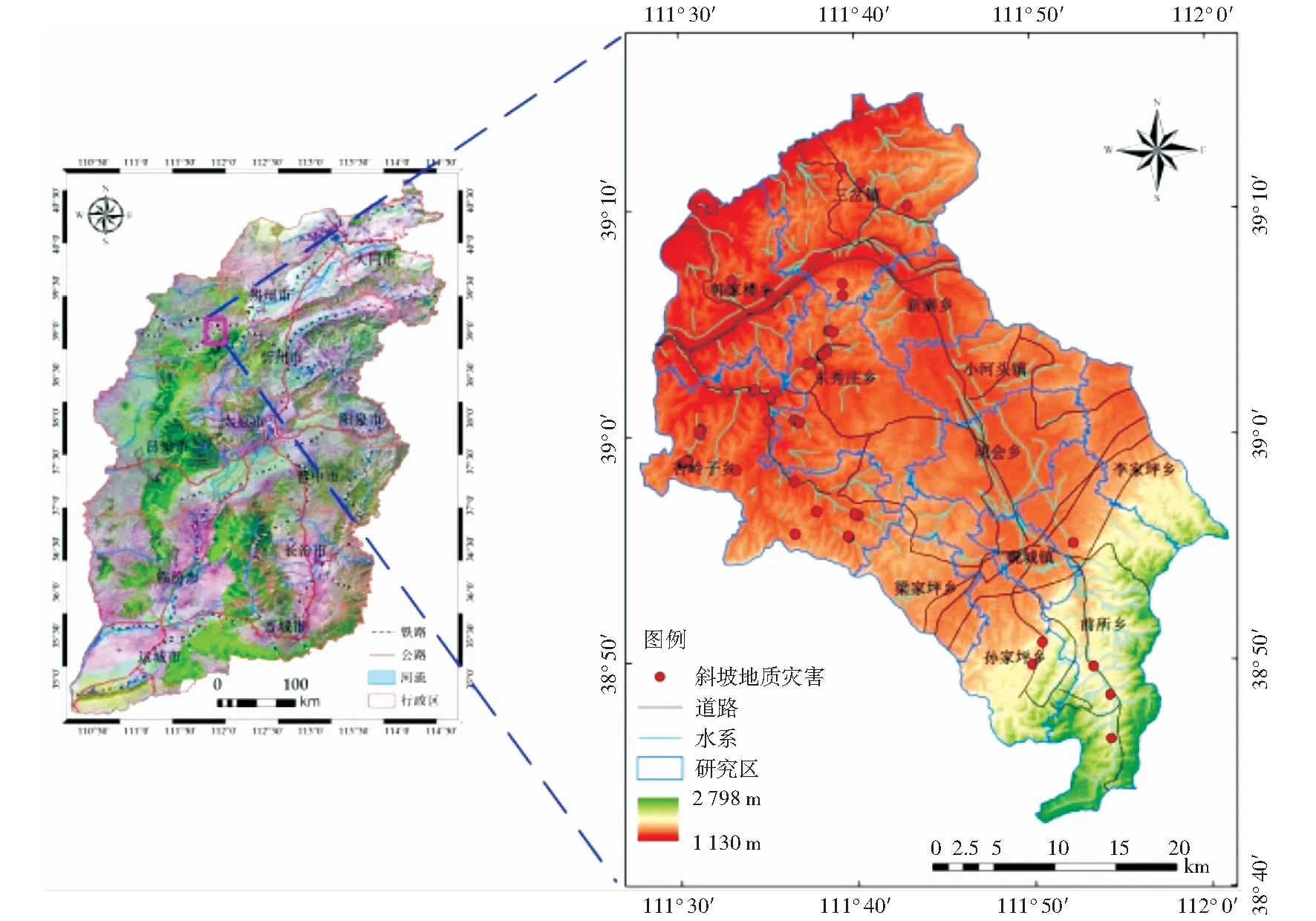
图1 研究区地理位置图Fig.1 Geographical map of the study area

地形地貌表现为：地势东南高，为变质岩森林山区；西北低，属于典型的晋西北黄土高原黄土地貌形态；中部地势平坦，为黄土盆地平川区。

区内分布有横山断裂、安塘-五寨隐伏断层和青阳岭及小口村断层，地表水均属黄河水系，主要有朱家川河、县川河、岚漪河三大水系。

1.2 数据源

1.2.1基础数据

基于2017年五寨县地质灾害分布及易发程度分区图(1∶50 000)矢量化成果，提取了研究区斜坡地质灾害点53处，其中，崩塌49处，主要为黄土崩塌，不稳定斜坡4处，按规模划分为中型19处，小型34处。同时提取了研究区地层岩组、地质构造、基础地理信息等数据。研究区内的地层岩组由老到新依次为：

1.2.2DEM数据

DEM数据主要用于数字地形因子提取，本文基于地理空间数据云(http://www.gscloud.cn/)下载ASTER GDEM V2数据作为DEM数据，并完成了预处理与裁剪。该数据空间分辨率约为30 m，垂直分辨率为20 m，空间参考为WGS84/EGM96.

1.2.3遥感影像数据

遥感影像主要用于植被覆盖(NDVI)提取，本文基于地理空间数据云(http://www.gscloud.cn/)下载2017年8月11日Landsat8数据，完成了影像预处理与裁剪。该数据空间分辨率约为30 m，波段8为15 m分辨率的全色波段。

本文的空间分析、结果统计与制图等工作基于Arc GIS软件进行，而敏感性评价基于SPSS Modeler软件进行。

2 敏感性评价方法

2.1 CF模型

CF模型是一个概率函数，由Shortliffe E H和Buchanan B G于1975年提出。1986 年，HECKERMAN[17]对该模型进一步改进，用来分析研究影响某一事件发生的各因子的敏感性。根据待评价区域内已知的地质灾害隐患点，假设地质环境变化可以忽略，已发生灾害与将来可能发生的灾害具有发育地质环境强相似性，通过CF方法对影响地质灾害发生的各个因子的不同区间进行敏感性计算，获取不同分级区间的CF值，利用CF值判断地质灾害发生的可能性。

CF值的取值范围为[-1，1]，当 CF>0时，值越大发生灾害的可能性越大；当CF<0时，值越小发生灾害的可能性越小；而当 CF=0时则无法确定是否会发生灾害[15]。

CF值计算公式如下[8]：

(1)

式中：Pa为某一特征a的条件概率；Ps为研究区域的灾害点数量与面积之比；CF为地质灾害发生的确定性系数。

2.2 SVM模型

支持向量机基于机器学习理论，最早由VAPNIK在20世纪60年代用于研究小样本情况下提出的[18]，被认为是目前针对小样本估计和预测学习的最佳理论，在灾害敏感性评价中应用较多[11,19]。

yi(wTxi+b)≥1，i=1,…,n.

(2)

(3)

SVM利用核函数使非线性分类问题得到解决，目前，SVM常用核函数主要有线性核函数、多项式核函数、径向基核函数和Sigmoid核函数。灾害敏感性评价中径向基核函数应用较多[11]，但针对不同的研究目的，应对比4种核函数预测精度，选择最优核函数建立SVM预测模型。

2.3 I模型

为了评价CF模型、SVM模型与CF-SVM模型的精度和敏感性分区效果，本文采用I模型与SVM模型的组合(I-SVM模型)作为对比模型。

I模型利用信息量描述影响因子的数量和质量，从而决定地质灾害的发生概率，在地质灾害敏感性评价中有大量应用[7]，信息量计算公式为：

(4)

式中：xi代表评价单元内所取的因子等级；I(Xi,H)为因子xi对地质灾害所贡献的信息量；S为研究区面积；Si为研究区内含有因子xi的面积；N为研究区内地质灾害总数；Ni为发生地质灾害区域中含有因子xi的数量；I为评价单元中的综合信息量；n为影响因子数量。

3 斜坡地质灾害敏感性评价

斜坡地质灾害的发生与孕灾环境及诱发因素密切相关，合理选择评价因子是保障敏感性评价结果可靠性的关键，而准确掌握斜坡地质灾害空间分布特征是开展基于统计思想的灾害敏感性评价的重要前提。目前，地质灾害空间分布特征研究众多[20-23]，同时，文献[24]认为岩性、坡度、坡向、起伏度、与河流距离和与主要道路距离是影响云南镇雄县滑坡发育的主要因子。文献[25]则对滇东北滑坡孕灾环境的高程、坡度、坡向、降雨量、岩石硬度、距道路距离、距河流距离和距断裂距离8个因子进行了敏感性分析，为合理选择评价因子进行了探索。这些研究工作的展开，为斜坡地质灾害敏感性评价因子选择及可靠获取[26]提供了参考。

3.1 评价因子

地形地貌与地质因素是地质灾害发育的控制性因素，人类工程活动则引起斜坡体稳定性减弱，诱发崩塌与滑坡灾害，河流冲刷进一步降低了斜坡坡脚的稳定性，而植被覆盖则具有保持水土的作用，对保障坡体稳定性具有积极作用。

针对评价因子分级标准，有研究者采用定量计算选取阈值划分等级[12]，也有研究者根据以往经验与灾害点分布规律进行因子状态分级[7，11]。

本文在前期研究基础[22，26]上参考现有研究[7,11,24-25]，从地形地貌(高程、坡度、坡向、地势起伏度)、地质因素(地质构造、地层岩组)、人为动力(道路工程扰动)和自然因素(河流水系、NDVI)四个方面选取9个因子构建敏感性评价因子(表1)，综合考虑进行了评价因子分级。

表1 研究区斜坡地质灾害评价因子及分级表Table 1 Classification of evaluation factors of slope geological hazard sensitivity in the study area

3.2 评价因子分级CF值

以表1中9个评价因子的分级指标进行分级统计，并以公式(1)、(4)分别计算得到各评价因子不同分级的CF值和I值(表2).

表2 各因子分类等级CF值计算结果表Table 2 Calculation results of CF of classification level of each evaluation factor

3.3 多模型敏感性评价

现有研究中通常采用已知灾害点的70%或80%作为训练点建立预测模型，剩余的30%或20%作为验证点评价预测模型精度[8,11,19]。本文随机选取总灾害点的70%和相同数量的非地质灾害点作为模型建立训练样本，非灾害点在Arc GIS中随机生成，灾害点与非灾害点之间的点间距不小于500 m，剩余30%的灾害点和相同数量的非灾害点作为模型预测精度评价样本，非灾害点同样在Arc GIS中随机生成且点间距不小于500 m.

3.3.1CF模型与I模型评价

CF模型和I模型均需要考虑评价因子之间的相关性，如果因子之间高度相关，则会影响模型的预测精度，甚至出现错误的结果。本次采用相关系数R来衡量评价因子之间的相关度，R的取值范围为[-1,1]，|R|越接近1，因子之间的相关性越高，反之则越低。

利用SPSS软件进行了各评价因子相关性分析，结果表明：

1) CF模型中，高程与道路工程扰动(R=0.867)，坡向与地势起伏度(R=0.714)之间有较强相关性，综合考虑后剔除高程因子与坡向因子，以剩余7个影响因子构建敏感性评价因子集，采用CF模型进行研究区斜坡地质灾害敏感性评价。

2) I模型中，高程与地层岩组(R=0.683)之间有较强相关性，综合考虑后剔除高程因子，以剩余8个影响因子构建信息量评价因子集，采用I模型进行研究区斜坡地质灾害敏感性评价。

3.3.2SVM模型评价

在SVM样本训练中利用4种核函数分别训练，对比4种核函数SVM模型预测准确率，径向基核函数SVM模型预测精度明显较其他三种核函数SVM模型预测正确率高。因此，本文采用径向基核函数SVM模型进行研究区斜坡地质灾害敏感性评价。

3.3.3CF-SVM模型评价

该模型是对CF模型和SVM模型的组合，利用CF方法计算得到各个影响因子的分级CF值，以CF值替代分级统计结果作为SVM模型的分类数据，并将其作为训练样本数据，采用径向基核函数SVM模型进行样本训练，进而对研究区栅格数据进行预测，得到研究区斜坡地质灾害敏感性评价结果。

3.3.4I-SVM模型评价

该模型构建方法与CF-SVM模型相同，是对I模型和SVM模型进行的组合，首先计算得到各个影响因子的分级I值，然后利用分级I值作为SVM模型的分类数据，并将其作为训练样本数据，同样采用径向基核函数SVM模型进行样本训练，最后对研究区栅格数据进行预测，得到研究区斜坡地质灾害敏感性评价结果。

3.4 评价结果

利用自然间断点法将研究区划分为4个敏感性等级，分别为极高敏感区、高敏感区、中敏感区和低敏感区，在Arc GIS平台对采用CF模型、I模型、SVM模型、CF-SVM模型和I-SVM模型得到的斜坡地质灾害敏感性分区进行制图(见图2)和分区统计(见表3).

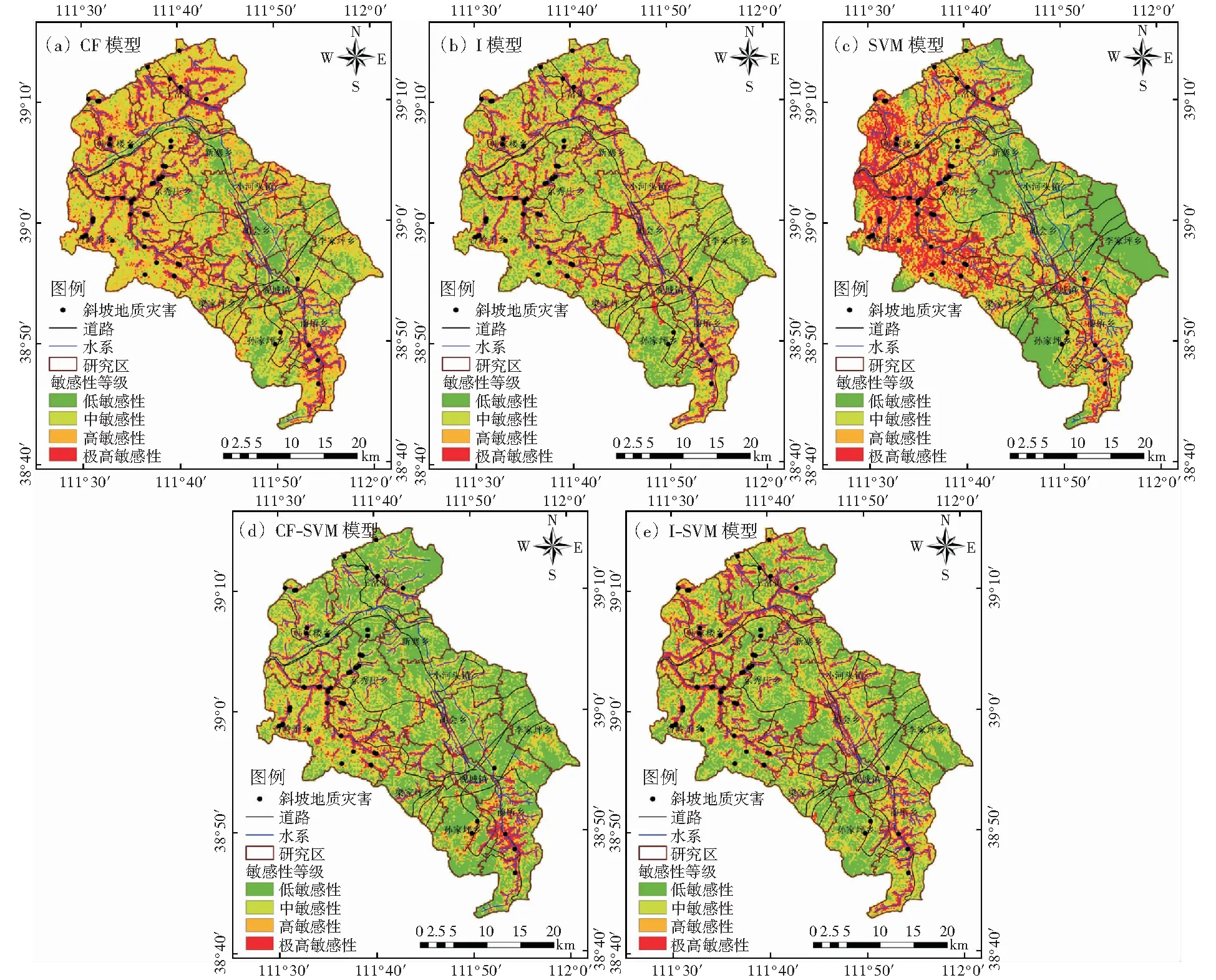
图2 研究区斜坡地质灾害敏感性分区图Fig.2 Slope geological hazard sensitivity zoning in the study area

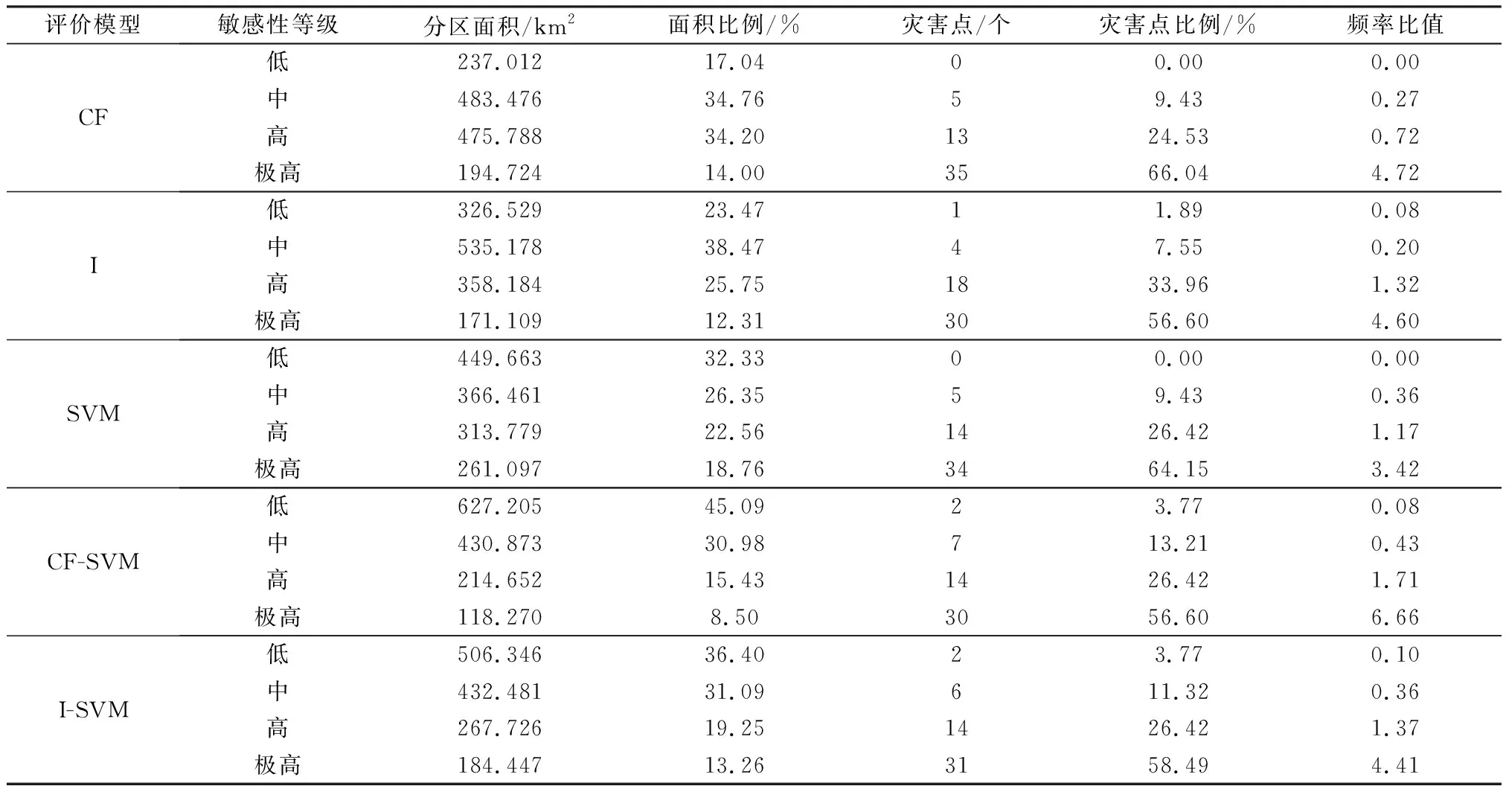
表3 研究区斜坡地质灾害敏感性分区统计表Table 3 Statistical table of slope geological hazard sensitivity zoning in the study area

图2显示，CF模型、I模型、CF-SVM模型和I-SVM模型的极高敏感区主要分布于研究区的河道沟谷，部分沿道路分布，呈明显的树杈状，而SVM模型的极高敏感区主要分布于五寨县西部的黄土丘陵区，该地区沟谷纵横、水土流失严重，是黄土崩塌发育的潜在隐患区，同时东南部土石山区部分分布。五种模型的极低敏感区主要位于五寨县中部平原区，但CF-SVM模型分布更广泛。CF-SVM模型与I-SVM模型所划分极高敏感区分别保持了CF模型与I模型的特点，沿水系走向分布，而低敏感区则保持了SVM模型的特点，主要分布于中部平原区，并向全域扩散分布。

表3可以看出，CF模型所划分极高、高敏感区总面积为670.512 km2，占研究区总面积的48.20%，灾害点分布占总灾害点的90.57%；I模型所划分极高、高敏感区总面积为529.293 km2，占研究区总面积的38.06%，灾害点分布占总灾害点的90.56%；SVM模型所划分极高、高敏感区总面积为574.876 km2，占研究区总面积的41.32%，灾害点分布占总灾害点的90.57%；CF-SVM模型所划分极高、高敏感区总面积为332.922 km2，占研究区总面积的23.93%，灾害点分布占总灾害点的83.02%.I-SVM模型所划分极高、高敏感区总面积为452.173 km2，占研究区总面积的32.51%，灾害点分布占总灾害点的84.91%.五种模型的频率比值均随敏感性等级升高而递增，表明五种模型的频率比值与敏感性等级之间具有良好的正相关。极高敏感区的频率比值从大到小依次为：CF-SVM模型(6.66)>CF模型(4.72)>I模型(4.60)>I-SVM模型(4.41)>SVM模型(3.42)，表明CF-SVM模型在满足极高敏感区较小面积分布较多灾害点的能力最好。同时，CF模型与SVM模型的低敏感区频率比均为零，小于CF-SVM模型的0.08，但是CF-SVM模型的低敏感区面积占比为45.09%，大于CF模型与SVM模型的17.04%和32.33%，同时也大于I模型与I-SVM模型的23.47%和36.40%，更符合低敏感区较大面积分布较少灾害点的实际情况。

3.5 精度检验

目前，一般采用ROC曲线下面积AUC值进行敏感性评价模型精度等级评价，文献[19]给出了AUC值与模型精度等级之间的对应关系，具体如下：

1) 0.9～1.0，模型极好；

2) 0.8～0.9，模型非常好；

3) 0.7～0.8，模型表现好；

4) 0.6～0.7，模型一般；

5) 0.0～0.6，模型表现差。

本文采用ROC曲线评价精度，利用占总样本30%的未参与模型训练的16个灾害点和16个随机生成的非灾害点进行检验，五种模型的ROC曲线如图3所示，渐进显著性均小于0.05，表明五种模型均较好。CF模型、I模型、SVM模型、CF-SVM模型和I-SVM模型的AUC值分别为0.906、0.855、0.844、0.934和0.891，其中CF-SVM模型的AUC值大于其他四种模型，是五种模型中评价精度最高的模型，较CF模型、I模型、SVM模型与I-SVM模型的模型精度增益分别为3.09%、9.24%、10.66%和4.83%，而I-SVM模型较I模型与SVM模型精度增益分别为4.21%和5.57%.同时，CF模型与CF-SVM模型的精度为极好，而I模型、SVM模型与I-SVM模型的精度为非常好，均具有较高的适用性。

图3 ROC曲线图Fig.3 ROC curve

4 结论

1) CF-SVM模型是五种模型中评价精度最高的模型，较CF模型和SVM模型预测精度分别提升了3.09%和10.66%，较I-SVM模型预测精度高4.83%，其所划分研究区斜坡地质灾害低敏感区、中敏感区、高敏感区和极高敏感区的面积分别为：627.205 km2、430.873 km2、214.652 km2和118.270 km2，分别占研究区总面积的45.09%、30.98%、15.43%和8.50%，所分布灾害点分别占总灾害点的3.77%、13.21%、26.42%和56.60%.

2) 研究区斜坡地质灾害极高敏感区主要沿水系沟谷走向分布于县域西部的杏岭子乡、韩家楼乡和东秀庄乡西部黄土区，以及东南部前所乡的土石山区，是研究区地质灾害防控的首要区域。与2017年五寨县地质灾害分布及易发程度分区图(1∶50 000)对比，极高敏感区范围极大减小，为地质灾害精准防控提供了数据支撑。中、低敏感区范围显著增大，沿高敏感区向外扩展，为更高效、低成本、精准化开展研究区地质灾害防控工作提供了科学指导，避免了防控范围扩大化。

3) 敏感性分区图表明CF模型与I模型所划分敏感性分区结果较为相似，与SVM模型结果差异较大，同时CF-SVM模型与I-SVM模型结果差异明显。基于统计思想的CF模型和I模型需要考虑因子相关性，而SVM模型则需要更多的因子和样本数据进行学习，在小样本情况下组合CF模型(I模型)与SVM模型进行敏感性评价相比单模型评价具有明显的精度增益。综合频率比值、AUC值和敏感性分区图，CF-SVM模型融合了CF模型与SVM模型的优点，既保证了更多的斜坡地质灾害点分布于极高、高敏感区，模型精度极好，又保证了极高、高敏感区面积相对更小，符合斜坡地质灾害分布实际情况，是CF模型与SVM模型综合赋能预测结果的体现，也是区域内地质灾害数量较少情况下五种模型中最适用的敏感性评价模型。