基于水膜厚度理论的发泡充填料浆流动性能试验研究

张世玉，王 开，邱景平，郭镇邦

(1.太原理工大学 矿业工程学院，太原 030024；2.东北大学 资源与土工程学院，沈阳 110819)

近年来，充填采矿法被认为是有效且环保效果较好的开采工艺，引领了矿山无废、绿色、安全开采的发展方向[1-2]。目前充填矿山常用的充填体是以水泥作为胶结剂，尾砂作为骨料，制备60%～75%固体质量浓度的充填料浆充至井下采空区凝结而形成的[3]。由于料浆中含有大量水，在充填体凝结过程中，固体颗粒沉降，迫使多余的水排出，导致了充填体体积的缩小，这种现象在充填采场中的宏观表现为充填体难以接顶。此时，采场充填体无法保证上覆顶板在受到较大载荷时的稳定性[4-6]，不利于顶板上大规模机械化作业，而且会引起整体开采区域地表下沉。大量的工程实践总结出了一些常用的提高充填体接顶率的措施，如①提高充填料浆浓度；②提高料浆排水速度，多次充填；③提高下料点高度及多点下料等[7]。这些方法虽然能一定程度上提高充填接顶率，但实际操作及管理工作较为繁琐，很难达到理想的效果。鉴于传统充填体排水自缩的特性，张雄天等[8]在充填料浆中加入发泡剂使得充填体具备多孔结构，控制膨胀率使得充填体与顶板紧密接触且保证充填体具有维护采场稳定性所需的强度。相对于普通充填体，多孔结构对于爆破冲击波的吸收效果相对较好，这表明提高充填体自身的膨胀性能减少体积沉缩，即制备出具有膨胀特性的充填体来提高充填接顶率是可行的[9-12]。因此，发泡充填技术的研究对于尾砂的资源化利用、控制地表沉陷和提高充填效果等方面具有重要意义。

众所周知，充填料浆的流动性对于管道输送的效率具有重要影响，对于未发泡充填料浆来说，影响其流动性的主要因素有温度、胶结剂含量、固体颗粒尺寸、固体质量浓度、矿物添加剂以及化学添加剂等，且常常用扩展度表示料浆的流动性，国内外学者已经进行了大量的研究[13-18]。然而，针对发泡充填料浆的流动性研究相对较少，且其流动性影响机理尚不明确。因此，本文主要研究发泡剂量和骨料粒径对发泡充填料浆流动性能的影响，并基于水膜厚度理论分析流动性影响机理，为发泡充填在矿山的工程应用提供理论基础。

1 试验原料

1.1 胶结剂

图中Q表示石英，M表示莫来石，C表示石灰石图1 32.5普通硅酸盐(a)水泥粒径分布，(b)XRD物相Fig.1 (a) Particle size distribution, (b)XRD patterns of Ordinary Portland cement

1.2 充填骨料

为研究不同骨料粒径分布对发泡充填料浆流动性能的影响，选用傲牛全尾砂与两种粒径的石英砂(粗/细)进行混合(如图2(a)所示)，组成多种粒径分布的混合充填骨料，具体配比如表1所示。3种尾砂按表中配比均匀混合后，其粒度分布如图2(b)所示。由图中可知，细石英砂的比例越大，混合骨料的整体粒度越细，反之，粗石英砂的比例越大，混合骨料的整体粒度越粗。为有效表征混合骨料粒度的粗细程度，需选用粒度分布的特征参数，包括D20、D50、D80、均匀系数(Cu)及曲率系数(Cc).这些参数尽管可以从整体上较为详尽地描述颗粒或粉体的粒度分布状况和级配优良与否，但是数据过多，难以分析。因此，有学者假设颗粒为理想球体，从统计学的角度，描述一批颗粒或粉体的大小，即用平均粒径来描述粒度分布状况[19]，平均粒径则可表示为D(4，3)，11种粒径尾砂的各粒径特征参数如表2所示。

表1 混合充填骨料组成(质量分数)Table 1 Mix ratios for the tailings and silica tailings(mass fraction)

图2 (a)全尾砂和粗/细石英砂粒径分布，(b)混合充填骨料粒径分布Fig.2 Particle size distribution of (a) tailings and coarse/fine silica sand, (b) mixed aggregates

表2 混合充填骨料的粒径参数Table 2 Particle parameters of mixed aggregates

1.3 发泡剂

本次研究所采用的发泡剂为30%浓度的过氧化氢(H2O2)溶液。为减少发泡剂的敏感性对试验数据的影响，在制备发泡充填料浆时，需在均匀搅拌料浆之后加入30%的过氧化氢(H2O2)溶液再次均匀搅拌30 s.需要注意的是每次制备发泡充填料浆所采用的搅拌转速及时间相同，室内温度相差控制在±2 ℃.

2 试验方案及方法

2.1 试验方案

为研究发泡剂量对发泡充填料浆流动性的影响，参考国内外发泡材料相关文献[12]和[20-22]及预试验，在控制发泡充填体膨胀率小于15%的情况下，暂定发泡剂量为胶结剂质量的0%、0.8%、1.6%、2.4%、3.2%，具体试验方案如表3所示。

表3 发泡剂量对充填料浆流动性的影响试验方案Table 3 Effect of foaming agent dosage on the fluidity of fresh CFB

相同浓度及发泡剂量的料浆，骨料的粒径不同时，整体固体堆积密度相差较大对其流动性也会产生影响。因此，利用表2中的11种粒径的尾砂制备发泡充填料浆，发泡剂的添加量为0%、0.8%、1.6%、2.4%和3.2%(为胶结剂的质量分数)，胶结剂采用的是32.5普通硅酸水泥，灰砂比为1∶4，固体质量浓度为73%，详细试验方案如表4所示。

表4 骨料粒径对充填发泡料浆流动性的影响试验方案Table 4 Effect of different particle size of filling aggregate on the fluidity of fresh CFB

2.2 测试方法

2.2.1流动度测试

由于充填料浆的固体质量浓度较小且骨料粒径一般较细，标准的塌落度试验较为费时且费料。所以，Mini塌落度试验渐渐地被众多的学者用来评估充填料浆的流动性能[23-24]。在Mini塌落度试验中，充填料浆的流动性通常用流动扩展直径(扩展度)来表征，而流动扩展直径是由屈服应力决定的，屈服应力与其在管道的输送性能相关。试验中采用的是Mini塌落度仪，尺寸如图3所示，上口直径50 mm，下口直径100 mm，高150 mm.按照ASTM-C143标准进行流动性测试，将搅拌均匀的料浆倒入塌落度仪中，捣实之后，垂直方向提起2 min后，测量任意两个垂直方向的扩展直径，取两者的平均值作为充填料浆流动性的指标(扩展度)。

图3 Mini塌落度仪Fig.3 Mini collapse meter

2.2.2流变特性测试

塑性黏度和Bingham屈服应力是表征新制水泥砂浆流变性能的常用指标[25]，本文中也用这两个指标来评价新制发泡充填料浆的流变特性。塑性黏度是施加在流体上的剪应力除以剪切速率[26]，新制发泡充填料浆作为一种非牛顿流体，其塑性黏度不是一个常数，取决于剪切速率。本文中采用NDJ-8S型旋转黏度计，测量范围为1×106～2×106mPa·s，3号转子，转速为30 r/min，测定新制发泡充填料浆的塑性黏度。在测量试验过程中，需要注意以下几个问题：1) 新鲜循环流化床样品之间的温差控制在±0.5 ℃以内；2) 量度用过的烧杯或圆筒形容器的尺寸，直径不应小于70 mm，高度不应小于100 mm；3) 扭矩使用值在10%～90%之间，一般情况下，最优扭矩值在50%～80%之间。

至于作者权（author’s right）传统下对作品思想感情表达的要求，则进一步要求创作者对其智力创作结果的主观意图。“人工智能创作”只不过是基于输入数据，按照算法得出结果，人工智能甚至都不能理解这些输出结果的意义，更谈不上价值判断、审美体验和情感表达这些人类创作的本质特征了。因此，纯粹“人工智能创作”仅具有形式上的表象，并非真正的智力创作，仅是模仿人类思维的计算结果而已，目前所谓的“强人工智能”以及神经网络深度学习技术也并未突破其人工阈限达到真正意义上的智力创作。

至于Bingham屈服应力，则是静态屈服应力。更高的Bingham屈服应力导致更高的浆料固化性质[27]。新制发泡充填料浆在外力作用下产生的剪应力一旦超过Bingham屈服应力，就会发生可见流动。在本文中，采用自制的Bingham屈服应力测试装置进行Bingham屈服应力的测量，如图4(a)所示[28]。相应地将测定的Bingham屈服应力定义为等效Bingham屈服应力。

图4 自制膨胀充填料浆(CFB)等价屈服应力测试装置Fig.4 Measurement device for equivalent Bingham yield stress of fresh CFB

测试时，采用精度为0.001 N的拉推力计测量拉力，预埋在新制发泡充填料浆中的薄塑料板尺寸为宽5 cm，高7.5 cm.在每个新制发泡充填料浆样品不同位置测量4次，如图4(b)所示，将4次测量的平均值作为等效Bingham屈服应力，具体计算公式可以表达为：

(1)

式中：τ0为等价屈服应力，Pa；F1,F2,F3和F4分别为4个位置测试的拉力值，N；b和h为塑料片的尺寸，mm.

2.2.3堆积密实度测试

堆积密度测试方法分为干堆积法和湿堆积法。干堆积法测堆积密度受压实度的影响很大。为了避免上述问题，本文采用湿堆积法来测量发泡充填料浆的堆积密度[29]。湿堆积法的本质是在固体颗粒中加入不同量的水，固体质量分数先升高后降低，最大的固体质量分数即视为堆积密度。当含水量较低时，将形成许多液桥。这将减小固体颗粒之间的距离，随后导致固体质量分数的增加[30]。然而，随着水含量的增加，颗粒变得分散并且浆体体积增加，因此固体质量分数降低。与湿堆积法有关的更多细节可见参考文献[31]。图5为湿堆积法的试验步骤。

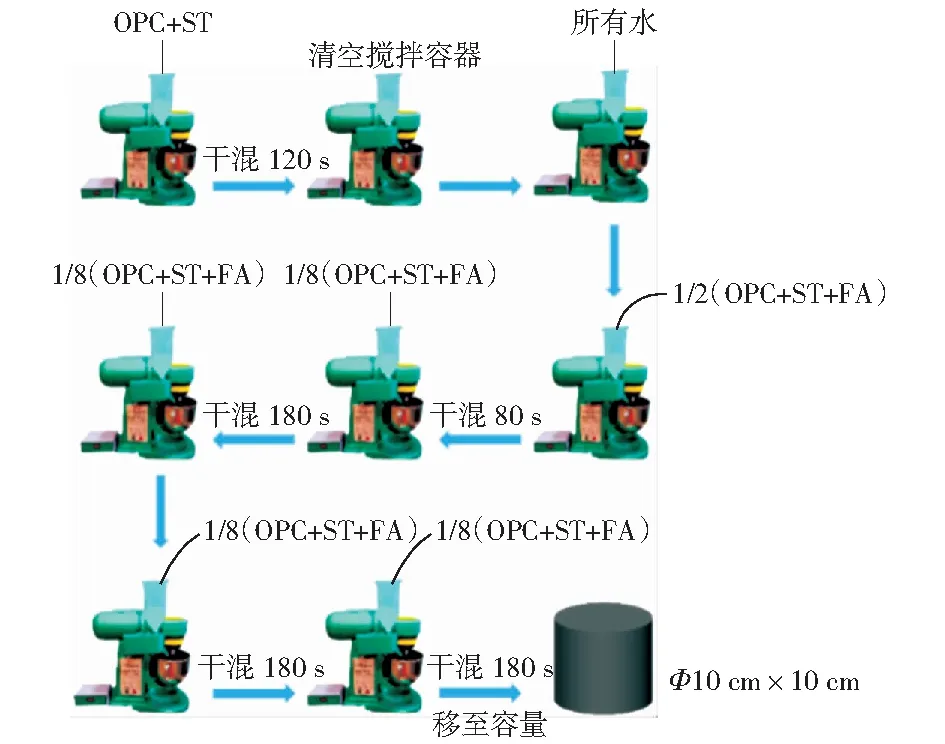
图5 发泡充填料浆的湿堆积法试验步骤Fig.5 Experimental steps of wet packing method for fresh CFB

3 结果和讨论

3.1 发泡剂量对发泡充填料浆扩展度和流变性能的影响

图6为发泡剂量对新制发泡充填料浆扩展度的影响。由图可以看出，发泡剂掺量的增加与充填料浆扩展度的变化成反比。例如，对于固体质量分数为73%的发泡充填料浆来说，随着发泡剂掺量从0%增加至3.2%，扩展度从255 mm降低至229 mm，降低了26 mm.这是因为浆体内部所存在的气泡数量随着发泡剂量的增加逐渐增多，气泡在浆体内部稳定存在时，表面会形成一定厚度的由水混合固体颗粒(包括充填骨料和胶结剂等)形成的膜。气泡数量增多，表面积增大，形态稳定存在时，其如同固体颗粒一样需要分担一部分自由水，那么，用于料浆流动的自由水就会相应减少，浆体扩展度就会降低。此外，还可以观察到，将发泡剂量由0%增加至3.2%时，不同固体质量分数对应的扩展度变化也是不同的。同时，对于相同固体质量分数的发泡充填料浆来说，发泡剂量从0%增加至3.2%时，扩展度降低的幅度是不相同的，大致呈现出下降的趋势。比如，对于固体质量分数为76%的发泡充填料浆来说，随着发泡剂掺量从0%增加至0.8%再到3.2%时，扩展度的减少量分别为14.5 mm、9.9 mm、8.7 mm和0.2 mm.这就说明发泡剂量达到3.2%及以上时，对较高质量分数(76%)的料浆流动性产生影响较小。这里通常可以用较高质量分数(76%)的料浆具有较大的塑性黏度和Bingham屈服应力，气泡难以继续移动、扩展和融合从而保持分布状态稳定。

图6 发泡剂量对发泡充填料浆扩展度的影响Fig.6 Effect of foaming agent dosage on the spread diameter of fresh CFB

图7为发泡剂量对发泡充填料浆流变特性的影响。由图可以看出，发泡剂量的增加与发泡充填料浆的流变参数(等效Bingham屈服应力和塑性黏度)的变化呈正比。例如，对于固体质量分数为73%的发泡充填料浆来说，随着发泡剂掺量从0%增加至3.2%，发泡充填料浆的等效Bingham屈服应力从34.1 Pa增加到50.0 Pa，增加量为15.9 Pa，而塑性黏度从0.58 Pa·s增加到0.92 Pa·s，增加量为0.37 Pa·s.发泡剂量增大时，气泡的数量增多，发泡充填料浆整体的堆积密度会发生变化，气泡与固体颗粒间的间隙增加，对于含水量一定时，会吸收更多的自由水填充间隙。同时，发泡充填料浆整体的总表面积增大，同样会分担更多自由水，这样用于减少气泡与固体颗粒之间摩擦力的水就会减少，从而使浆体变得不易流动，料浆变得难以剪切且黏度增大。同时根据文献[25][32-33]的研究可知，水泥料浆的流变特性与流动性能存在着密切的关系，流动性增大时，流变参数也相应变大。

图7 发泡剂量对发泡充填料浆流变特性的影响Fig.7 Effect of foaming agent dosage on the rheological properties of fresh CFB

3.2 骨料粒径对发泡充填料浆扩展度和流变性能的影响

由表2中统计的发泡充填骨料各粒径参数可知，体积平均直径D(4，3)随着粗石英砂添加比例的增大而增大，随着细石英砂添加比例的减小而减小。堆积密度P随着粗石英砂的添加比例的上升而下降，随着细石英砂添加比例的上升而增加，说明尾砂整体颗粒粒径较大，添加细颗粒会减小粗骨料之间的间隙，从而增大堆积密度。此外，发泡充填骨料粒径分布宽度与体积平均直径的变化成正比，例如，当发泡充填骨料体积平均直径从192 μm增加至398 μm时，粒径分布宽度则从0.776增加至0.908，说明发泡充填骨料粒径分布是越来越窄。

图8为发泡充填骨料体积平均直径和堆积密度对发泡充填料浆扩展度的影响。由图8(a)可知，发泡充填料浆的扩展度随着体积平均直径的增大而增加。这是由于体积平均直径较小的发泡充填骨料具有较大的比表面积，需要更多的自由水包裹固体颗粒，致使用于浆体流动的自由水减少，扩展度降低[34]。此外，扩展度的变化量因发泡剂添加量的不同而表现出差异。例如，当充填骨料的体积平均直径从398 μm降低至192 μm，发泡剂添加量分别为0%、0.8%、1.6%、2.4%和3.2%对应的扩展度降低量为26.37%、23.33%、19.55%、18.06%和17.24%.这主要是因为发泡剂量的增加使得充填料浆中气泡数量增多，与固体颗粒相似，气泡会分摊一部分自由水形成液膜，减少料浆自由水含量而降低扩展度。发泡剂添加量越大，扩展度降低的效果越明显。如图8(b)所示，随着堆积密度的增加，发泡充填料浆的扩展度明显降低。由表2可知，细充填骨料具有较小的Rosin Rammler系数[35]，粒径分布宽度大，这会增大物料体系的堆积密度而降低固体颗粒之间的间隙。当与水混合时，水会优先充填间隙，然后再包裹固体颗粒，剩余的自由水供颗粒间润滑流动[16，31，36]。细充填骨料中固体颗粒间隙需水量虽小，但用于包裹颗粒的需要水量大(比表面积大)，整体上用于颗粒间润滑流动的自由水减少。

图8 发泡充填料浆扩展度随(a)体积平均直径；(b)堆积密度的变化Fig.8 Effect of (a) volume moment mean diameter; (b) packing density on the spread diameter of fresh CFB

发泡充填骨料粒径分布对发泡充填料浆流变参数(等效Bingham屈服应力和塑性黏度)的影响如图9所示。可以看出，与流动性的变化趋势相反，等效Bingham屈服应力和塑性黏度的变化均与体积平均直径成反比。例如，当骨料体积平均直径从192 μm增加至398 μm时，发泡剂添加量为0%，0.8%，1.6%，2.4%和3.2%的发泡充填料浆等价屈服应力分别从45.82 Pa，48.28 Pa，52.19 Pa，55.34 Pa和58.31 Pa降低至25.84 Pa，27.54 Pa，30.35 Pa，32.81 Pa和34.09 Pa.而相应的表观黏度分别由1.18 Pa·s，1.29 Pa·s，1.41 Pa·s，1.5 Pa·s和1.63 Pa·s降低至0.45 Pa·s，0.52 Pa·s，0.29 Pa·s，0.66 Pa·s和0.71 Pa·s.粒径分布变大时，颗粒间隙增大与比表面积减小相互作用使得用于润滑颗粒流动的自由水增加，从而降低了流动阻力，等效Bingham屈服应力和塑性黏度也相应降低。此外，还可以看出发泡充填料浆的等效Bingham屈服应力随着粒径增加均匀降低，而塑性黏度则表现出先增大后减小的趋势。由OUATTARA et al[37]研究可知，料浆的剪切屈服应力与扩展度关联较为密切，而与塑性黏度则没有表现出明显的关联。参照图8(a)扩展度随体积平均直径变化的增量是相对均匀的，证实了发泡充填料浆的剪切屈服应力与扩展度关联密切。

图9 发泡充填骨料粒径对发泡充填料浆流变特性的影响Fig.9 Effect of particle size on the rheological property of fresh CFB

3.3 发泡充填料浆流动性影响机理分析及讨论

根据上述实验结果，发泡剂对充填料浆流动性或流变性有重要影响。不可否认的是，发泡剂产生的气泡是研究发泡充填料浆流动性或流变性的关键。为量化研究气泡对充填料浆性能的影响，这里引入水膜厚度理论进行相关研究。水膜厚度理论(WFT)多用于水泥浆体或砂浆领域，其认为在料浆系统中包含的水(W0)可以分为两部分，即空隙填充水(W1)和额外自由水(W2).额外自由水包裹在固体颗粒表面形成水膜(图10).如果体系总水量低于或等于空隙填充水量，则塌落度值很小，浆体可视为不具有流动性[38]。因此，额外水量是浆体具有流动性的首要条件。浆体中水膜厚度值的具体计算公式如下[39]：

(2)

式中：μw是水体积与固体颗粒体积的比值；μs是空隙比，按μs=(1-φ)/φ计算(φ是固体颗粒的堆积密度)；固体颗粒的比表面积为As.

图10 (a)水膜，(b)扩展度与水含量关系的示意[40]Fig.10 Schematic illustration of (a) water film and (b) relationship between flow spread and water content

由于浆体中气泡的粒径分布是未知的，因此气泡比表面积的获取更加困难。但掺入发泡剂之后，浆体的膨胀率很容易通过实验获得，即气泡球的体积分数已知。此外，通过湿测法，混合体系的堆积密度是已知的。通过假设气泡球的粒径分布，然后将气泡球视为填料以一定的体积分数(根据膨胀率而定)混入固体颗粒体系，若最后得到的体系的堆积密度与湿测法结果一致(通过颗粒流软件PFC3D实现)，则假设成立，如若不一致则继续假设。根据最终假设得到的气泡球的粒径，可以进一步得到体系的比表面积。具体的步骤如图11所示。

图11 颗粒比表面积的计算流程Fig.11 Calculation process of the specific surface area of system particles

3.3.1PFC堆积模拟误差标定

值得注意的是，利用上述方法进行气泡粒径的估计不可避免地存在误差，在PFC3D中采用自重堆积，其获得的堆积密度的结果必然小于湿测法得到的结果。若直接采用两者相等时的气泡粒径进行比表面积的计算，显然是错误的。因此，首先必须进行模拟值与实验值的标定，即确定两者的换算关系。

首先利用真空筛制备4种粒径的尾砂样品(100～500 μm)，具体的粒径分布见表5.根据湿测法，可以分别得到各自的堆积密度。其次本文PFC3D模拟计算假设尾砂为球形，在有效区内生成40×40×60的封闭墙体，并在此封闭墙体内生成特定级配的尾砂颗粒[41]。尾砂颗粒在重力作用下重新堆积，直至平衡状态。本文选用线性模型，颗粒弹性模量选取1 GPa，密度为2.5 g/cm3，摩擦系数为0.5.图12和图13分别为颗粒模型及模拟堆积结果。

表5 尾砂样品粒径范围Table 5 Size range of tailing samples

图12 不同粒径分布的尾砂颗粒堆积的颗粒流模型Fig.12 Particle flow model of packing with different particle size distributions of tailings

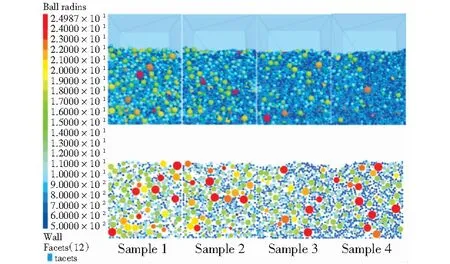
图13 尾砂试样的堆积结果Fig.13 Packing results of tailing samples

综上实验结果与模拟结果，可以得到两者的对比，如表6所示。可以看出，模拟值总小于湿测法测量值。这是合理的，因为在模拟时未施加振荡。WONG et al[31]表明振实过程会促进细颗粒填充空隙，从而增大堆积密度。根据两者的结果，可以得到模拟值与实验值之间的系数在1.1左右。因此利用该值进行掺入气泡后的模拟结果与实验结果的转换。

表6 模拟的堆积密实度与实验堆积密实度的对比Table 6 Comparison of simulated and experimental packing density

3.3.2水膜厚度对发泡充填料浆流动性能的影响

图14为WFT随发泡剂掺量的变化，当给定发泡剂掺量，WFT随着固体质量分数的增加而降低，这是由含水量降低造成的。例如，对于发泡剂掺量为1.6%的膨胀充填料浆，当固体浓度从68%升至76%，WFT则从0.594 μm降至0.531 μm.此外，可以观察到，不管固体质量分数如何，当发泡剂掺量从0%增加到3.2%时，WFT都显著降低。WFT的下降主要是由于比表面积与堆积密度的耦合作用。由于发泡剂掺量相对于浆体中的含水量很小，因此忽略发泡剂对浆体稠度的影响，即不考虑浆体稠度对气泡稳定性的影响。一方面，发泡剂掺量的增加导致系统中的气泡数量增加。若将气泡视为颗粒，发泡剂的掺入导致颗粒湿堆积系统重新堆积，即改变了系统的堆积密度。根据堆积理论[16]，在混合颗粒系统中存在三种物理效应(松散效应，壁效应和楔入效应)影响堆积密度的大小。对于本文的水泥-尾砂-气泡混合系统，大气泡边壁充当小颗粒的依附壁，小气泡楔入粗颗粒间隙，在壁效应和楔入效应共同影响下，体系的空隙体积增大，堆积密度减小(图15).另一方面，发泡剂产生气泡直径相较于本文使用的尾砂的粒径较低，这相当于系统中掺入了细填充料，导致颗粒体系比表面积增大。综上原因，随着发泡剂掺量的增加，体系WFT不断减小。值得注意的是，发泡充填料浆中所有WFT值都为正值，表明发泡充填料浆体系中的水足够填充固体颗粒之间的空隙。这也是充填体与混凝土的一个重要区别——混凝土中的WFT经常出现负值。从图14(a)也可以看出，随着发泡剂掺量的增加，无论固体质量分数如何，WFT均呈先急剧减小后缓慢下降的特点。这表明从WFT的角度来说，存在一个饱和发泡剂掺量，当发泡剂掺量达到该饱和值时，WFT变化不明显。该值的大小与充填体的材料性质有关，例如尾砂粒径、固体质量分数等。

图14 (a)不同发泡剂掺量及固体浓度对应的WFT；(b)体积平均直径对应的WFTFig.14 (a) WFT with foaming agent dosage at different solid contents; (b) WFT versus volume moment mean diameter

图15 壁效应及楔入效应Fig.15 Wall and wedging effects

图14(b)显示的是固定发泡剂掺量(1.6%)时，WFT随颗粒体积平均直径的变化。很明显，随着颗粒体积平均直径的增大，WFT逐渐升高。这主要是由于颗粒体积平均直径的增加，导致粒径分布宽度变宽，从而增大了颗粒系统堆积密度。此外，颗粒比表面积的减小也是一个原因。

流动性与WFT之间的关系如图16所示。总的来说，扩展度随着WFT的增大而增大。WFT越大，意味着颗粒间的润滑效应越强，导致屈服应力降低。根据QIU et al[16]的研究结果，充填料浆扩展度是屈服应力的宏观表征。为研究WFT的效果，通过回归分析得到了扩展度-WFT关系的最佳拟合曲线。在保持充填骨料粒径不变的条件下，发泡充填料浆扩展度与WFT呈现指数函数关系，拟合相关性系数R2值为0.96，表明发泡充填料浆的流动性主要依赖于WFT.值得注意的是，尽管相关性系数较高，但数据点在边界两侧的分散程度存在显著差异(WFT≈0.57 μm).当WFT>0.57 μm时，发泡剂掺量大约为0%～2%.此时数据点依附于拟合曲线。不同发泡剂掺量的发泡充填料浆的扩展度和WFT遵循同一趋势。这表明，无论发泡剂掺量如何，WFT仍然可以被视为控制新制膨胀充填料浆的唯一因素。当WFT<0.57 μm时，发泡剂掺量约为2%～3%.此时，数据点开始偏离拟合曲线，表明在发泡剂掺量较高时，WFT不再是控制发泡充填料浆的唯一因素。换句话说，发泡剂掺量本身的影响不可忽视。KWAN et al[43]在研究WFT和减水剂用量对砂浆流变性和黏结性的影响时，将这一现象归结为减水剂的“直接效应”和“间接效应”。一方面，发泡剂通过影响WFT来改变浆料的流动性(间接效应)。另一方面，发泡剂对流动性也有直接影响，这种影响不能通过WFT参数来表达。LI et al[44]认为，减水剂通过提高WFT和降低黏结性来改善水泥浆体的流动性。从本质上讲，这种降低黏结性的作用也可以看作是减水剂的直接作用。对比Kwan模型和本文的模型[43]，在发泡充填料浆中，流动扩展可以表示为WFT的一元函数，而在混凝土砂浆中流动扩展度则是WFT和减水剂含量的二元函数。也就是说，在发泡充填料浆中发泡剂的直接作用在一定程度上可以忽略，更准确地说，尽管WFT和发泡剂的直接作用的耦合效应仍然控制着膨胀充填料浆的流动性，但此时WFT的作用相对占优势。这可能归因于充填料浆中的含水量远高于混凝土砂浆中的含水量。因此，当发泡剂掺量较大时，发泡剂掺量是数据离散的根本原因。若要同时考虑发泡剂掺量的直接效应及WFT，需要引入新的指标，即GUO et al[15]提出的絮团膜厚度(FWFT)的概念。同理，当影响因素为骨料粒径时，WFT与扩展度也呈指数关系，相关性系数达到了0.98.此外，阈值WFT也出现且大小等于0.57 μm.值得注意的是，与发泡剂不同的是，骨料的絮凝成团作用是阈值WFT出现的原因，但本质上也是FWFT的影响。

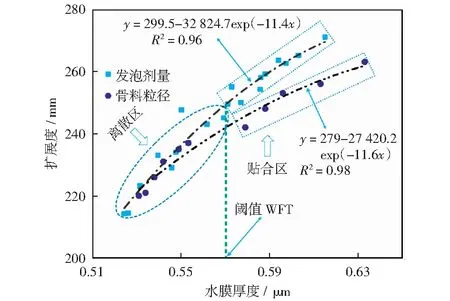
图16 扩展度与WFT之间的关系Fig.16 Relationship between spread diameter and WFT

4 结语

本文针对骨料粒径分布和发泡剂量对发泡充填料浆流动性能的影响进行了试验研究，并基于PFC3D构建气泡固体颗粒堆积模型，研究了发泡充填料浆水膜厚度随扩展度的演变规律。基于此，发泡料浆的流动度及随着充填骨料粒径的增加而增大，随着发泡剂量的增加而减小，前者与颗粒间隙及比表面积有关，而后者则与浆体中气泡的数量和分布形态有关。发泡料浆的流变特性(等价屈服应力和表观黏度)随着充填骨料粒径的增加而减小，随着发泡剂量的增加而增大。利用PFC模拟气泡与颗粒堆积模型，并检验模拟值与湿测法实验值的误差，标定误差系数为1.1.同时根据测定的堆积密度和PFC模拟得出的浆体总体表面积计算发泡料浆的水膜厚度，对料浆的扩展度与水膜厚度进行关联分析，相关性系数为0.96和0.98，由此可知，气泡改变了发泡充填料浆整体堆积密度和比表面积进而改变水膜厚度，影响料浆的流动性。