基于滑模控制与模糊控制的轨道列车制动力控制器设计

杨正专,杨 磊，刘寅虎，杜运哲，刘海洋，胡子佳

(南京中车浦镇海泰制动设备有限公司，南京 211800)

0 引 言

近年来，随着我国轨道交通事业的发展，交通运输行业对轨道交通载运工具安全、舒适、环保、高效等方面要求也日益提高。无论是运营高速化还是维护智能化，都对制动系统提出了更高的要求。作为轨道车辆的重要子系统，制动系统的发展也面临新的发展挑战。

电机械制动是一种直接利用电能驱动电制动缸产生摩擦力，从而使得运动减缓或停止的制动技术。相比于压缩空气制动与液压制动，电机械制动技术拥有响应时间短、控制精度高、控制效率和可靠性高以及节能环保等优势。

制动力闭环控制器设计过程中，需要充分考虑到所采用的传动机构及所带的负载对制动力闭环控制造成的影响。电机械制动的执行机构主要包括以下几个部分：电机、行星减速器、滚珠丝杠及制动摩擦块[1]，此时列车负载可以看作摩擦力负载。从现有的数学模型可知，电机的力矩输出和电流给定呈现出比较明显的线性关系，而其它传动机构则呈现出明显的非线性特征且制动力输出存在较大滞后[2]。控制模型的高度非线性给制动力的精准线性控制带来了极大挑战，而目前普遍采用的控制器仍然是经典PID控制器。

国内对电机械制动系统的力闭环控制器的研究还相对处于起步阶段，国外的研究也主要集中在航空器和汽车的制动力控制上，对于列车制动的制动力建立过程研究较少。文献[3]研究了模糊PID控制器在制动力控制中的应用，有效提升了制动力控制器在复杂非线性工况中的抗扰性能；文献[4]提出了一种基于电机转矩和传动机构模型参数的制动力观测器，实现了无力传感器的制动力闭环控制，减小了制动设备的体积，节约了成本；文献[5]提出了一种基于电机转子位置和电流的制动力观测器，实现无力传感器的三闭环制动力控制，提升了制动力的控制精度和可靠性，但是三闭环控制器的参数设计是一个较大的挑战；文献[6]提出了一种自适应模糊滑膜控制器来提升电机制动力矩的输出精度，同时通过液压制动补偿的方式来提升制动力的动态响应能力及跟踪精度，这种方式的控制效果较好但是应用范围受限；文献[7]提出了一种基于开关磁阻电机的力闭环鲁棒控制策略，控制效果较好，但是存在控制模型较为复杂，实现困难的问题；文献[8]提出了一种制动力动态控制方法，并进行了建模分析，但是该方法不适用于轨道列车制动，应用场景有局限性。

本文在对电机械制动系统进行合理建模的基础上，采用了制动力、电流双闭环控制结构，设计了一种制动力控制器。

1 系统方案及数学模型

1.1 系统方案

系统整体控制结构如图1所示，控制方案充分结合了传统PI控制、滑膜控制及模糊控制的优势，形成了一种高可靠性、高性能的组合制动力控制器。

图1 制动力电流双闭环控制框图

1.2 被控对象模型

电机械制动系统的控制器发出控制指令，通过功率驱动电路带动永磁同步电机运行，从而驱动机械执行机构动作，控制电机输出堵转转矩并建立制动力。因此，建立较为简洁可靠的机构模型对后续高性能控制器的设计至关重要。电机械制动系统的执行机构如图2所示，后文给出了各个机构的基本数学模型。

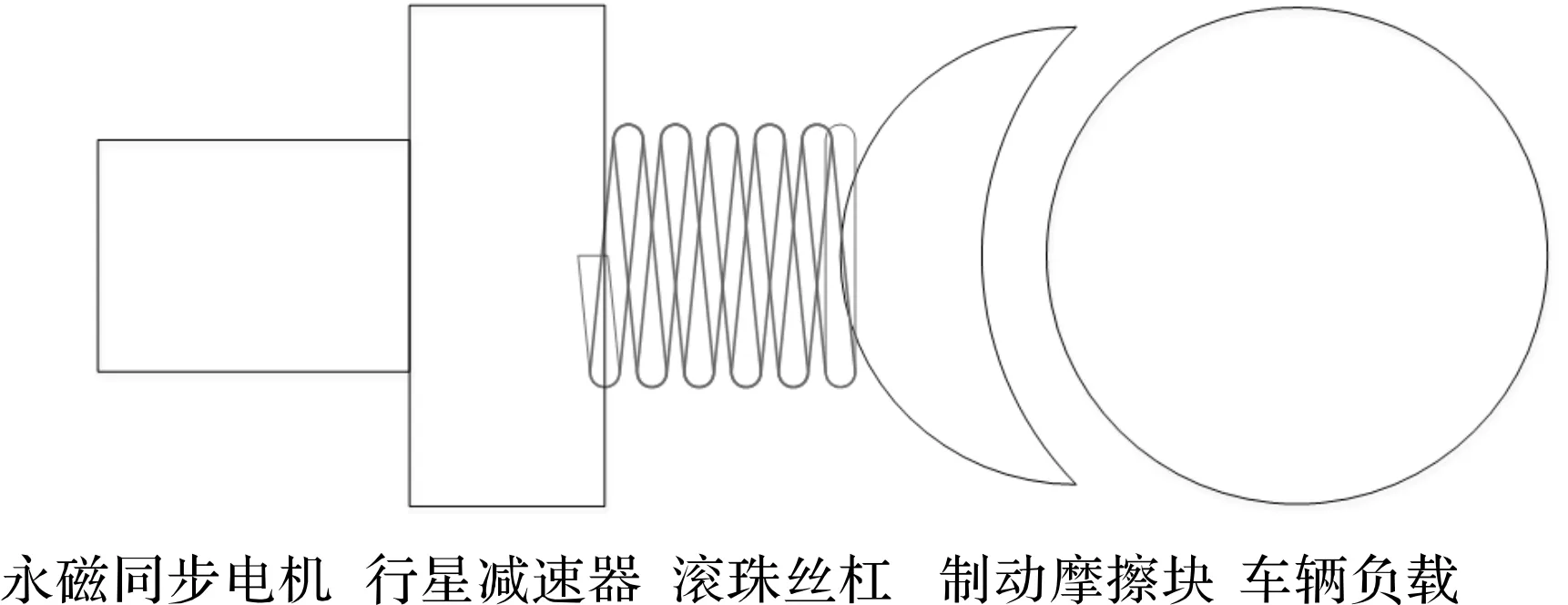
图2 制动力执行机构框图

1.2.1 永磁同步电机转矩方程

本文采用id=0的矢量控制方法对电机械制动系统中的永磁同步电机进行控制，并建立了永磁同步电机d-q坐标系数学模型，d-q坐标系下永磁同步电机的输出转矩方程为

(1)

式中，Te为电机电磁转矩；p为电机极对数；ψm为转子磁链；Ld，Lq分别为直轴电感、交轴电感；id，iq分别为直轴电流、交轴电流。

假定电流环控制特性较好的情况下，可简化得到如下的转矩电流方程：

(2)

1.2.2 理想行星减速器模型

由于行星减速器相比于滚珠丝杠等结构的延时较小，因此本文将其作为理想结构进行建模，忽略其动力学特性的影响。

Tx=Tei

(3)

(4)

式中，Tx为行星减速器输出力矩；i为减速传动比;θm为永磁同步电机机械转角；θx为行星减速器转过角度。

1.2.3 滚珠丝杠数学模型

由于滚珠丝杠将电机旋转运动转化为直线运动，这个转换过程满足如下关系：

(5)

其中，θL为滚珠丝杠螺母转过角度；x为滚珠丝杠的轴向位移；Ph为滚珠丝杠的导程。

考虑了动力学特性的滚珠丝杠螺母运动微分方程如下：

(6)

式中，JL为滚珠丝杠的等效转动惯量；bL为滚珠丝杠的等效机械阻尼系数；kL为滚珠丝杠的等效扭矩刚度；θL为滚珠丝杠转过的角度；Tx为减速器输出转矩;Tm为滚珠丝杠的阻力矩；TL=kLθL，为滚珠丝杠的输出力矩。

1.2.4 制动摩擦块数学模型

制动摩擦块的运动微分方程为

(7)

2 组合制动力控制器设计

轨道车辆制动过程中，制动器摩擦块接触面、路面状况及滚珠丝杠工作状态都处于不断变化的过程中，电机械制动系统的运行工况呈现高度的非线性及不确定性特征。因此，在保证较高控制精度的同时，电机械制动系统也对制动力控制器提出了较高的鲁棒性要求。高性能、强鲁棒性的制动力控制器是电机械制动系统的关键性难点。

传统PID控制器在控制过程中需要引入微分控制，由于微分控制在实际应用中的诸多缺陷与不足，实际工业应用中广泛采用了PI控制来进行控制器的设计。PI控制具有较高的稳态控制精度，但是其动态响应性能略显不足；滑模控制器动态性能较好，但是滑模面抖振问题也限制了滑模控制在高精度控制中的推广应用。本文提出了一种结合模糊PI控制的变增益二阶滑模组合控制器，旨在实现两种控制方式的优势互补，实现高性能的制动力控制。

2.1 变增益二阶滑模控制器

由理论分析可知，输出制动力大小与制动摩擦块的挤压形变程度成正比，而摩擦块的挤压形变程度则可以由滚珠丝杠位移角进行换算，其中输出制动力与滚珠丝杠位移角的换算关系如下：

(8)

因此，只要将制动力的控制转化为对滚珠丝杠位移角的控制，即可设计出相应的制动力滑模控制器。

(9)

(10)

为了避免微分噪声对系统性能的影响，保证系统的稳定性，本文采用了一阶滑模面进行控制器设计。本文所设计的一阶滑模面如下：

(11)

滑模控制的趋近律主要有以下几种形式：

(1)等速趋近律

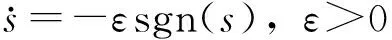
(2)指数趋近律

(3)幂次趋近律

(4)一般趋近律

(5)二阶趋近律

在进行了大量的测试分析之后，本文发现采用二阶趋近律能够有效抑制滑模面附近的抖振问题，获得更好的动态及稳态性能，因此在设计中选用了二阶趋近律。

则基于二阶趋近律可求得如下参考滑模切换面：

(12)

则求得模型的参考给定状态量为

(13)

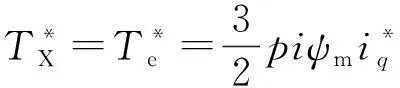
(14)

即得到了q轴电流的给定值计算公式。

由于实际工况中制动力参考值变化范围较大，传统固定增益系数的滑模控制器难以满足实际控制需求。因此在假定系统模型为高阶线性定常系统的前提下，为了保证滑模控制器在参考制动力变化时始终能够保持较好的输出特性，本文设计了一种线性的增益变化规则，即滑模控制器增益随给定制动力大小线性变化，调整规则如式(15)～式(16)所示。

ksmo=λkFref

(15)

αsmo=λαFref

(16)

式中，ksmo为等速趋近项增益；αsmo为幂指数趋近项增益；λk为等速趋近项增益系数；λα为幂指数趋近项增益系数；Fref为给定制动力。

由上式可知，我们只需要确定λk、λα即可实现滑模控制器的变增益调节。为了达到这一目的，本文选取了5 kN作为基准制动力，选择了此时的一组较为合适的增益作为基准增益k0、α0，则增益系数如下：

(17)

(18)

2.2 模糊PI控制器

模糊PI控制器是模糊控制和传统PI控制器的结合体，能够通过模糊控制规则在线修改PI控制器参数，从而获得较高的稳态、动态性能及良好的鲁棒性。

2.2.1 选择控制器输入和输出

本文采用了两输入的模糊控制器，定义了E、EC两个输入变量。EC有7个模糊状态{NB、NM、NS、Z、PS、PM、PB}，为了提升控制精度，E设置了8个模糊状态{ NB、NM、NS、NZ、PZ、PS、PM、PB }；本文中定义了ΔKp、ΔKi两个输出变量，两个输出变量互相独立，各自有7个模糊状态{NB、NM、NS、Z、PS、PM、PB}。

2.2.2 输入量及输出量的模糊化

经过仿真过程中的多次测试，最终确定了输入量和输出量的隶属函数如图3～图6所示。

图5 输出量ΔKp的模糊化

图6 输出量ΔKi的模糊化

2.2.3 模糊决策

结合前人已有的模糊控制规则设计经验[9]，设计了本模糊控制器的模糊决策规则。

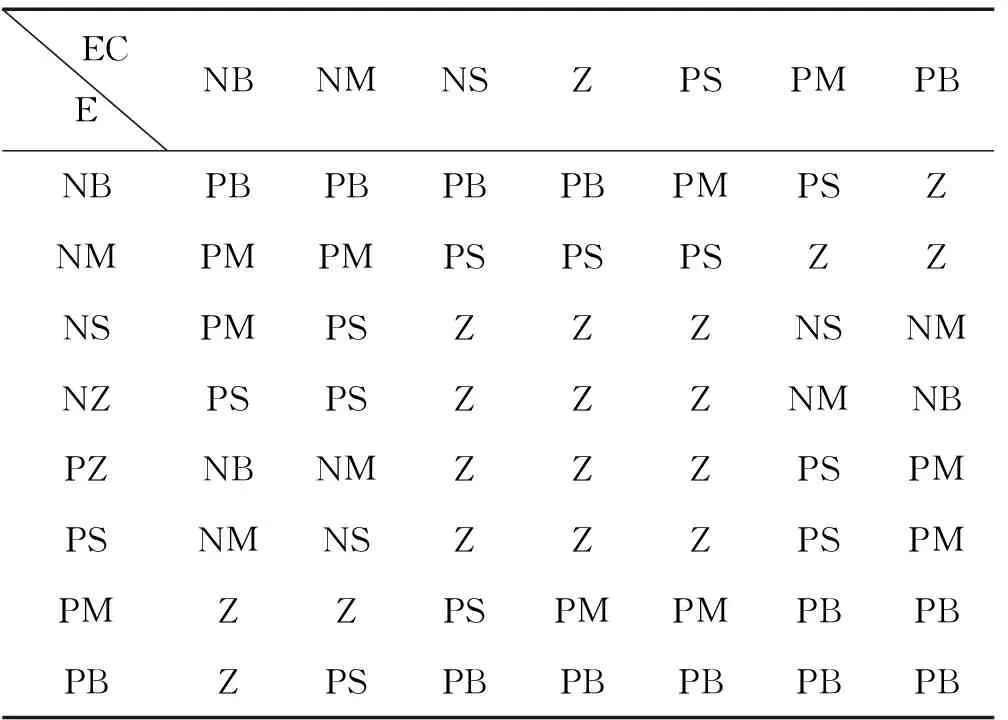
表1 ΔKp调整表

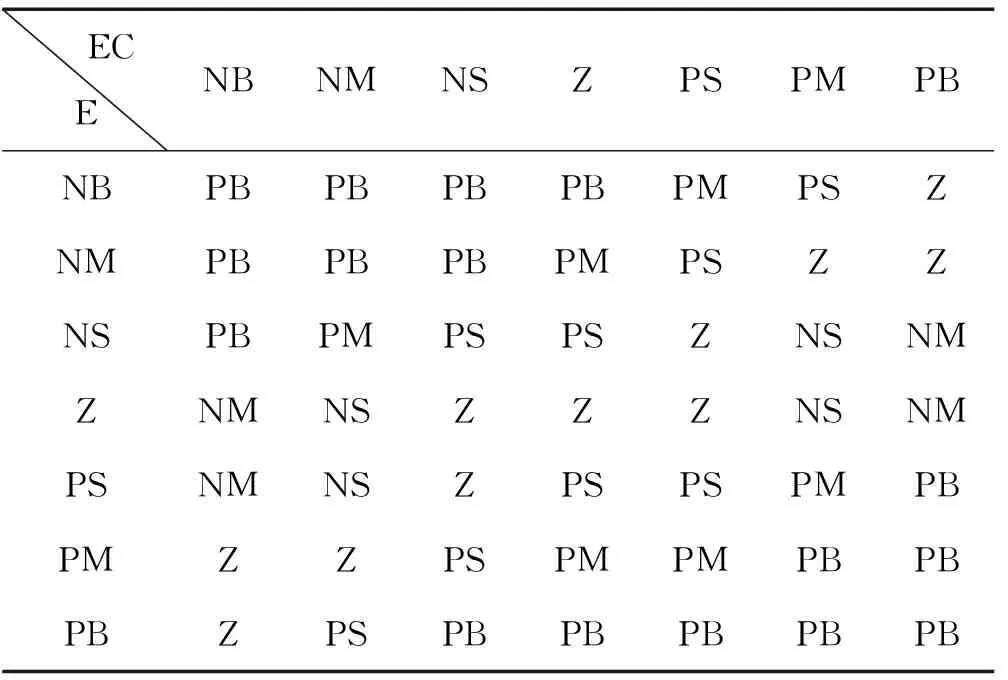
表2 ΔKi调整表

2.2.4 输出量的反模糊化

在使用模糊系统进行控制时，为了求得受控系统的输出，必须将控制输出解模糊化。目前常用的几种解模糊化方法有最大隶属度函数法、重心法、加权平均法。

(1)最大隶属度函数法

d0=max(μd(d)),d∈D

最大隶属度函数法只能考虑模糊推理结果中隶属度最大的点，不能充分考虑模糊隶属函数的形状，通常应用在一些要求控制精度不高的场合。

(2)重心法

重心法综合考虑了模糊隶属函数的形状，可以获得更加平滑的输出，通常应用在一些要求控制精度较高的场合。

(3)加权平均法

加权平均法的可以根据实际情况选择，在工业控制领域获得了广泛的应用。

为了简化设计及获得较为平滑的输出，本文采用了重心法来进行解模糊化计算。

2.3 组合控制器

传统PI控制具备稳态精度高的特点，但是动态性能稍差；变增益二阶滑模控制虽然能在获得与传统滑模控制几乎相同的动态性能的同时，有效削弱稳态振荡幅值，但是稳态性能仍然远远逊色于传统PI控制。采用模糊控制能够有效提升控制的鲁棒性，但是鉴于制动力参考值变化范围较大的特点，直接采用模糊控制可能会使得系统的控制分辨率及控制精度降低。为了充分利用传统PI控制、变增益二阶滑模控制和模糊控制的优势，本文设计了更加灵活的组合控制策略。

当制动力误差较大时，组合控制器为传统PI控制器与变增益二阶滑模控制器的组合，二者按照一定比例并联输出。一方面，变增益滑模控制器可以补偿传统PI控制器动态响应能力不足的问题；另一方面，传统PI控制器可以降低滑模控制器所需的控制增益，有效减小滑模控制器的稳态振荡。控制结构如图7所示。

图7 传统PI与变增益二阶滑膜组合控制框图

当制动力误差小于一定阈值时，组合控制器为模糊PI控制器与变增益二阶滑模控制器的组合。模糊PI控制器表现为一种强阻尼控制器，能够有效抑制滑模控制器振荡及负载扰动等带来的制动力波动，有效增强了控制器的稳态控制鲁棒性。同时，较小的控制范围也让模糊控制器的控制精度得到了保障。稳态控制框图如图8所示。

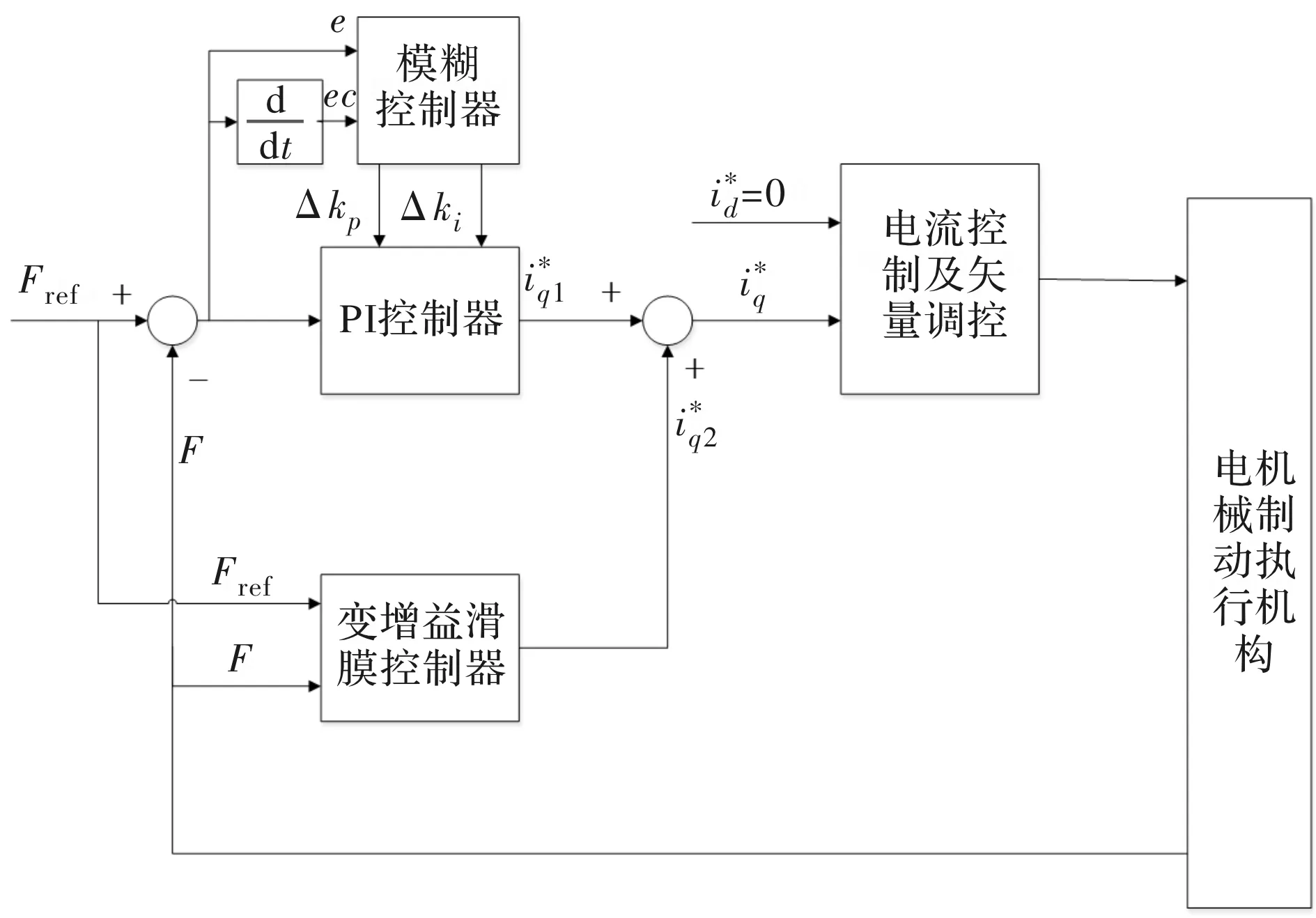
图8 模糊PI与变增益二阶滑膜组合控制器结构框图

3 仿真及实验验证

3.1 仿真验证

制动力控制仿真所用的永磁同步电机参数如下：

下表中列出了执行机构的主要参数：

依据上述参数，在MatlabSimulink中搭建了传动机构模型，对经参数优化的PID控制器和结合模糊PI及变增益二阶滑模结构的组合控制器分别进行了相应的仿真分析。

3.1.1 阶跃给定分析

设置参考制动力Fref=5 kN，则可得到带低通滤波器的传统PID控制器控制效果如图9所示。

图9 传统PID控制器制动力阶跃响应

相同给定条件下，组合控制器的制动力响应如图10所示。

图10 组合控制器制动力阶跃响应

表5中分别给出了带低通滤波器的PID控制器、结合传统PI的变增益滑模控制器及结合模糊PI的变增益滑模控制器的阶跃响应性能参数。

表5 阶跃给定性能比较

由图8可知，带低通滤波器的传统PID控制器控制性能很容易受到滤波器参数与系统噪声的干扰，控制性能受到影响。由图9可见，结合模糊PI的组合控制器抑制超调及稳态扰动的能力明显强于传统PID控制器。在表5中，本文对三种控制器的动态性能进行了定量分析，直观展现出了组合控制器的显著优势。

3.1.2 斜坡给定分析

设置参考制动力Fref=5 kN，参考斜率kF=10 kN/s，可得到带低通滤波器的传统PID控制器斜坡响应效果如图11所示。

相同给定条件下，组合控制器的制动力斜坡响应如图12所示。

图12 组合控制器制动力斜坡响应

表6中分别给出了带低通滤波器的PID控制器、结合传统PI的变增益滑模控制器及结合模糊PI的变增益滑模控制器的斜坡响应性能参数。

表6 斜坡给定性能比较

由上述图表分析可知，组合控制器的初始响应速度略慢于传统PID控制器，超调量大于传统PID控制器，但是上升时间与传统PID控制器所需要的时间几乎相同，调节时间与稳态误差均远远小于传统PID控制器。因此，在斜坡给定的情况下，组合控制器的综合性能仍然优于传统PID控制器。

3.2 实验验证

为了进一步验证所设计控制策略在实际工况下的控制效果，基于TMS320F28335搭建了硬件实验平台，实验平台如图13所示。实验所用的电机参数及制动系统参数与仿真一致，如表3及表4所示。

表3 永磁同步电机仿真参数

表4 执行机构仿真参数

图13 制动力实验平台

为了直观比较所提出的组合控制策略与传统PID控制策略在控制性能方面的差异，在相同制动力给定条件下采用两种控制策略分别进行了实验。间隔5 s设定的制动力给定序列依次为13 kN、23 kN、33 kN、21 kN、9 kN、10 kN。图14为采用传统PID控制方法的制动力响应实验波形。制动力在阶梯型阶跃给定条件下可以实现制动力的快速跟踪，但制动力调节超调超过10%。制动力调节达到稳态的时间也较长，调节时间超过3 s，并且控制器抑制扰动的能力较差，制动力响应中存在显著毛刺。图15给出了采用组合控制器产生的制动力响应实验波形，可以看出阶跃给定下制动力调节超调小于5%，调节时间小于1 s,由外部扰动产生的制动力毛刺显著消失。由实验结果的对比可知，组合控制策略实现了制动力控制动态性能和稳态精度的提升，且有效增强了控制器抑制复杂工况下外部扰动的能力。

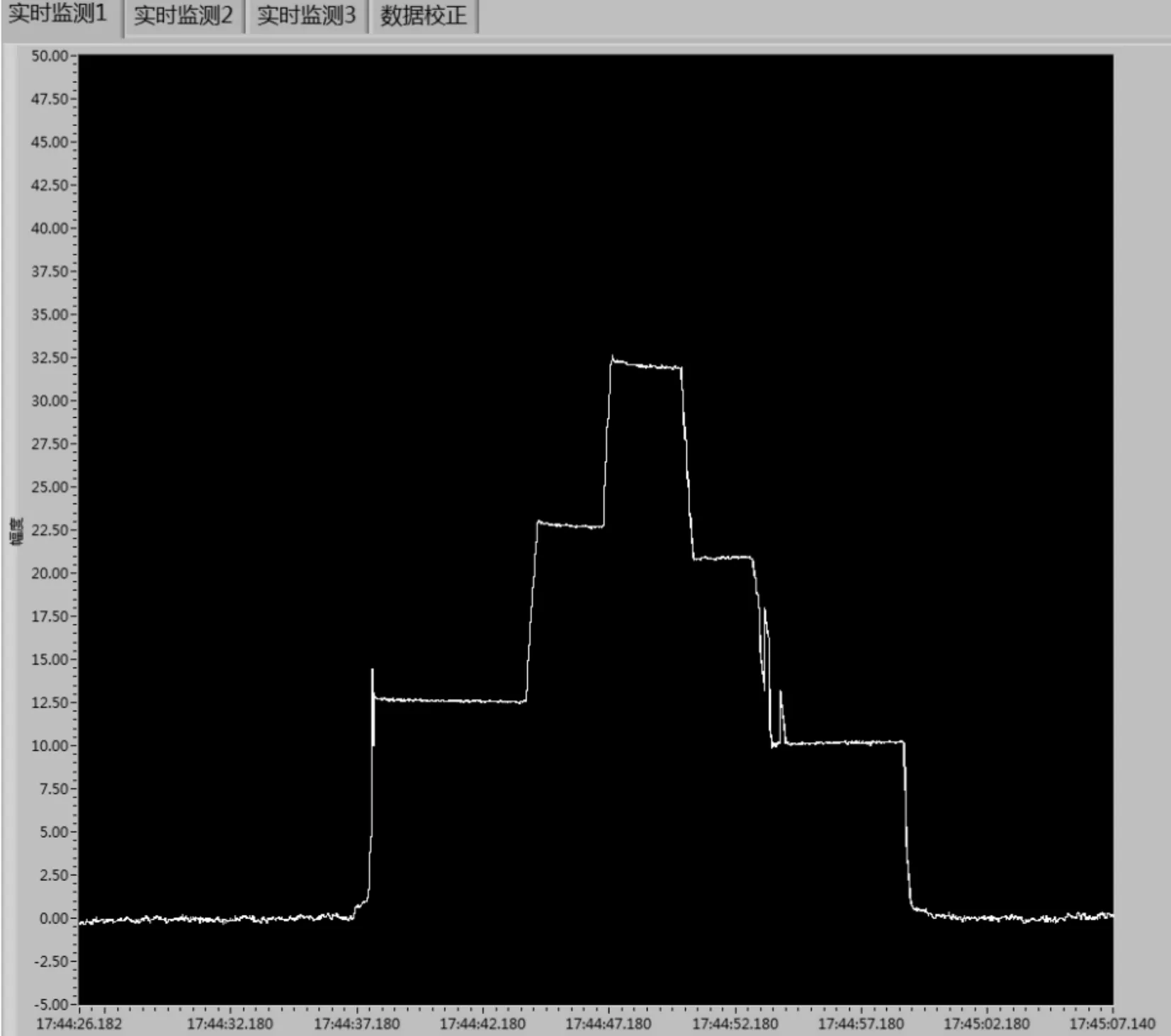
图14 传统PID控制器制动力响应

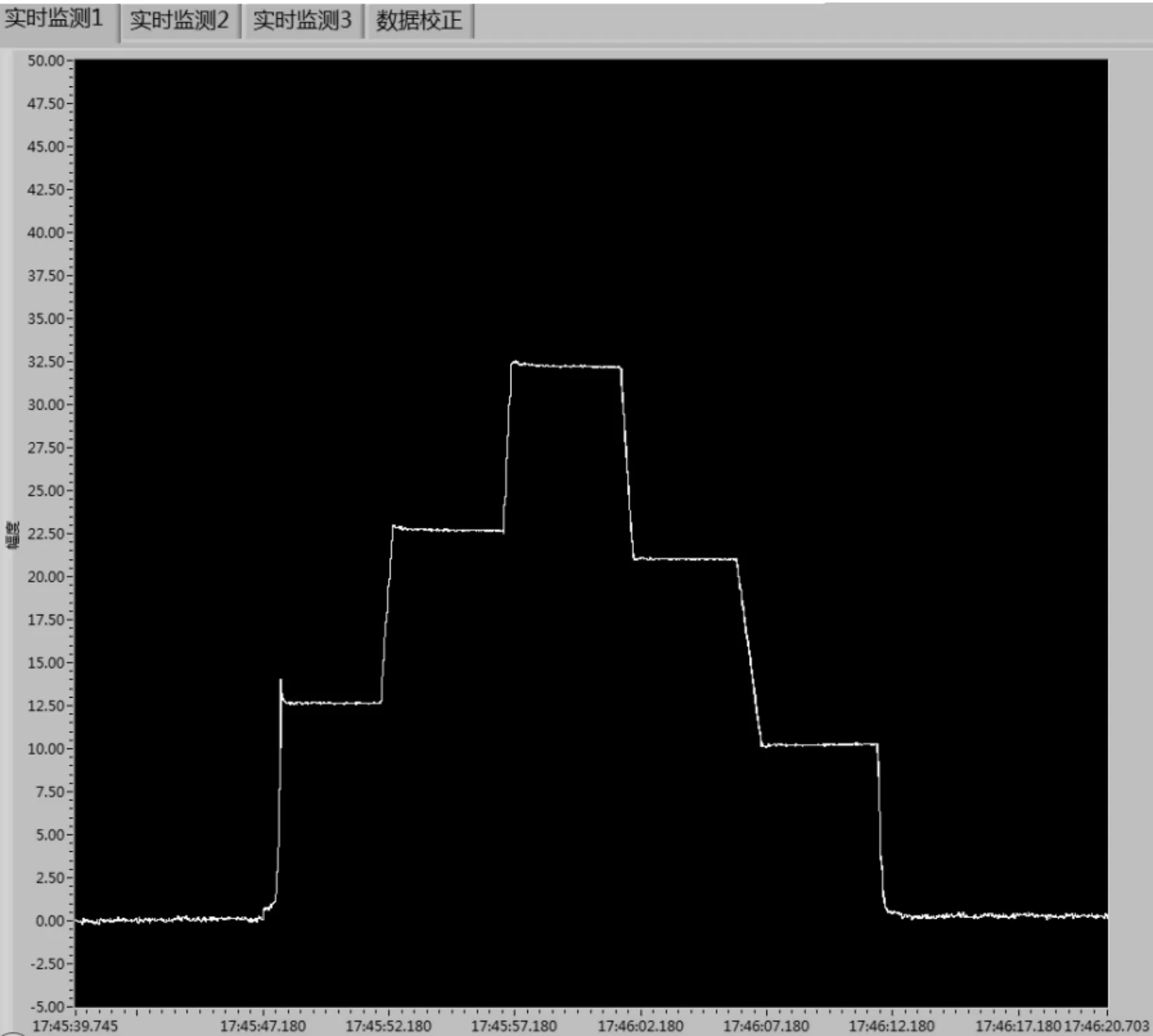
图15 组合控制器制动力响应

4 结 论

轨道列车制动系统工作环境较为恶劣，参数摄动及外部干扰等扰动较大，同时制动系统机械结构带来的转动惯量和阻尼导致系统惯性延时较大，而列车运行的安全性和舒适性需要却同时对列车的动态性能和稳态精度提出了极高的要求，常规的控制器往往无法同时满足要求。本文充分考虑了传统PI控制器、滑模控制器及模糊控制各自的优势与局限性，设计了一种具备更好性能、更高可靠性的组合控制器。以传统PI控制器作为设计基础，结合变增益滑模控制有效改善了制动力控制器的动态性能，稳态情况下引入模糊控制有效提升了控制器的稳态输出精度和抗干扰能力，实现了制动力响应的动态性能与稳态精度的同时提升。本文所提出组合控制器的控制性能在仿真和实验中得到了验证。