Henry 范围内粗糙孔隙中气体的等量吸附热与吸附选择性*
康艳霜 王海军 孙宗利
1) (河北大学化学与环境科学学院,保定 071002)
2) (河北农业大学理学院,保定 071001)
3) (河北大学,河北省化学生物学重点实验室,保定 071002)
4) (河北大学,药物化学与分子诊断教育部重点实验室,保定 071002)
5) (华北电力大学数理系,保定 071003)
Henry 系数和等量吸附热是表征气体吸附中气-固作用的重要参数.为了更好地理解气体在粗糙孔隙中的吸附特征,首先构造并计算了矩形波纹粗糙狭缝及其外势分布.进一步,采用经典统计力学研究了狭缝中H2分子在低压范围内的纵向Henry 系数和等量吸附热.研究结果表明,粗糙狭缝的几何形貌和基板间距等因素可对狭缝中气体的纵向Henry 系数和等量吸附热产生显著的影响与调制作用.进一步,在Henry 范围内计算了CO2/H2二元混合物气体在矩形波纹粗糙狭缝中的吸附选择性,并研究了狭缝几何形貌的调制作用.此外,还研究了不同形状的凸起对气体吸附性质的影响.相关的结果可为理解多孔材料中气体的吸附、分离和提纯等过程提供可靠的理论依据,并有望为设计与研发新型纳米功能材料提供有益的参考.
1 引言
当前,“双碳”达标和清洁能源是世界各国努力研究的重要课题,而碳封存、储氢以及超级电容等也已成为学者们关注的热点问题.在此类研究中,掌握功能材料的吸附特性是理解相关问题的关键所在[1].等温吸附量和等量吸附热是表征材料吸附特征的重要信息来源.其中,等温吸附量体现材料的吸附能力及其对气体分子的吸附亲和力[2].通常,固体材料的吸附能力可由Henry 系数来衡量.另一方面,等量吸附热是吸附过程中体系焓变的负值[3],且可理解为单位数量的气体分子由其体相等温等压地转移至吸附相的过程中所释放的热量.van’t Hoff 定律表明,等量吸附热不仅是对吸附过程的热力学描述,还是气体的Henry 系数对温度的响应灵敏度的量度[4].因此,掌握材料中气体的Henry系数和等量吸附热是准确理解其吸附行为及其特征的重要前提.
在气压极低的Henry 范围内,气体分子间的相互作用可忽略不计,等温吸附量与气压呈线性关系.此时,可用单个气体分子来探测吸附剂的表面形貌及其势能分布.基于其势能分布,可进一步算出体系的Henry 系数和等量吸附热,并对吸附剂材料的吸附能力和吸附行为予以表征[5].近年来,Steele 10-4-3 势能函数被广泛用于Henry 系数和等量吸附热的相关计算[6].此外,Maurer 等[7]通过固体Hamaker 常数来构造吸附势,并以此计算了低压范围内单组分气体的Henry 系数.Jiang 等[8]采用Monte-Carlo (MC)模拟研究了具有不同拓扑结构的碳材料附近的N2气体的Henry 系数和等量吸附热.Do 等[9]采用巨正则MC (GCMC)模拟计算了碳纳米管附近Ar 气体的Henry 系数和等量吸附热,并研究了二者在管内、外的区别.LeVan 等[4,10,11]采用MC 模拟计算了不同受限空间中气体的Henry 系数和等量吸附热,并着重研究了受限空间尺寸的影响.
在以上的研究报道中,大多以光滑基板或由光滑基板构成的孔隙为研究对象.事实上,固体材料的表层常会出现缺陷或杂质,进而导致其表面附近的势能分布发生变化.这将影响固体材料的吸附特征,并使之呈现不同于光滑基板情况下的特征[12].最近,Wongkoblap 等[13]和Loi 等[14]计算了粗糙表面附近的气体的吸附等温线和等量吸附热.研究表明,与光滑基板模型相比,粗糙基板模型的结果与实验结果符合得更好.然而,该工作仅研究了某些特定尺寸的粗糙表面对等量吸附热的影响,粗糙表面的几何形貌的调制作用并未涉及.鉴于Henry系数和等量吸附热在气体吸附中的重要性,研究和阐明粗糙孔隙的几何形貌对二者的调制是十分必要的.
在气体混合物的分离和提纯过程中,不同组分与固体材料间相互作用的差异起着关键的主导作用.它不仅影响固体材料对不同气体组分的吸附能力,还导致各组分间的吸附竞争,即吸附选择性[15].近年来,除直接的实验测量外[16−18],不同学者已采用密度泛函理论[19]、GCMC 模拟[20−24]、分子动力学模拟[25,26]等理论方法对气体混合物在光滑孔隙中的吸附选择性进行了较为系统的研究.然而,关于粗糙孔隙中气体混合物的吸附选择性的研究却鲜有报道.
因此,本文将构造几何波纹粗糙狭缝,并在Henry 范围内对孔隙中H2的Henry 系数、等量吸附热,以及CO2/H2二元混合物气体在狭缝中的吸附选择性等问题进行计算.同时,将系统研究粗糙狭缝的几何形貌、缝宽等因素对以上吸附特征的影响和调制作用.
2 模型与理论
2.1 粗糙狭缝中的气-固作用势
假设粗糙狭缝由两个相同的矩形波纹粗糙基板构成,且每个粗糙基板均由光滑基板和等间距分布的凸起组成,如图1(a)所示.基板上的凸起沿x方向无限延伸,沿y方向具有空间周期λ=w1+w2,且在z方向具有高度D=MΔ.其中,w1为凸起宽度,w2为相邻两凸起的间距,M为凸起中的原子层数,Δ 为层间距.在以下计算中,气体分子与固体原子间的相互作用由Lennard-Jones (LJ)势来描述:
由此可以看出,国外学者的研究是对财务共享服务模式的类型和演进过程总体上的划分和概括;国内学者则是依据理论,在实践中发现企业对于财务共享模式的实际选择和运用,并总结关键因素服务的影响。


图1 (a)粗糙狭缝示意图,绿色虚线包围的区域定义为狭缝中的I-类和II-类区域,蓝色虚线表示气体分子可达空间的边界;(b)单个粗糙基板附近的气体分子的外势分布为Vsub(y,z).计算中取w1=1.36 nm,w2=2.04 nm,M=3Fig.1.(a) Sketch of the rough slit pore.The regions surrounded by the green dash lines are type-I and type-II regions in the rough pore,while the blue dashed line stands for the boundary of the accessible volume of the gas molecular.(b) Profile of external potential Vsub(y,z) near a rough substrate with w1=1.36 nm,w2=2.04 nm and M=3.
其中,r为粒子间距离,εgs和σgs分别为气-固作用的阱深和有效直径,且二者满足Lorentz-Berthelot

以上计算结果表明,粗糙狭缝的几何形貌可对气体的KL和产生显著的调制作用.为更加全面地理解粗糙基板对气体吸附的影响,下面进一步计算受限于粗糙狭缝中的CO2/H2二元混合物的吸附选择性,即SCO2/H2.其中,基板形貌对SCO2/H2的影响如图8 所示.图中结果显示,SCO2/H2始终大于1.事实上,CO2的吸附优势可归因于CO2分子与固体原子的作用强度几乎是H2分子与固体原子的作用强度的两倍,如表 1 所列.即便如此,粗糙基板的不同的几何特征仍可以不同的方式调制SCO2/H2的大小.
图10(b)为H=1.50 nm 和D=R=0.34 nm的情况下,三角形和半圆形凸起狭缝中H2的KL和随w2的变化.其中三角形凸起取w1=0.68 nm.图10(b)与图6 中相同条件下结果的对比表明,KL和曲线随w2的变化趋势均与矩形凸起狭缝的趋势一致.但是,三角形和半圆形凸起狭缝的KL均大于矩形凸起狭缝在同条件下的值,而小于矩形凸起时的值.这同样可由上述竞争机制来理解.此外,三角形和半圆形凸起狭缝之间的结果对比表明,前者的KL比后者大,而却比后者小,原因在于当D=R且w1=2R时,与半圆形凸起狭缝相比,三角形凸起狭缝具有更大的可达空间和较弱的吸附势.需要说明的是,当w2较小时,三角形凸起狭缝的大于半圆形凸起狭缝的.这是由于在半圆形凸起狭缝中,相邻两凸起间的吸附势中有更大范围的强势部分与耗尽区域重合,进而削弱了气体分子的平均势能.
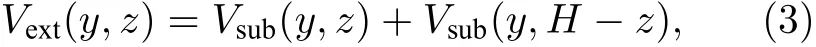
式中,Vsub(y,z)为单一粗糙基板的外势,H为缝宽.进一步,Vsub(y,z)可分解为源自光滑基板和凸起的贡献之和:

式中,光滑基板的贡献VSt(z)由Steele 10-4-3 势给出[6]:
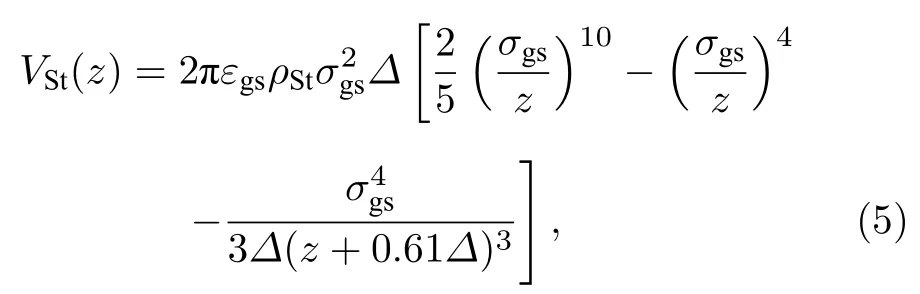
其中,ρSt为固体原子密度.(4)式中,Vt(y,z)表示来自基板上所有凸起的贡献.为方便,令Vm,n(y,z)表示第n个凸起上的第m层固体原子施于气体分子的外势.由粗糙基板上各凸起的平移对称性可知,Vm,n(y,z)可通过对第0 个凸起上的第m层固体原子施于气体分子的外势沿y方向进行平移来得出.基于以上分析,Vt(y,z)可表示为
大豆根系作为大豆的重要器官之一,在大豆整个生长发育、生理功能和物质代谢中发挥着重要作用。由于根系生长环境的特殊性,使得作物根系的研究远远滞后于地上部分,虚拟植物克服了传统方式下试验周期长、环境因素难以控制的缺点,大豆根系的虚拟研究具有重要现实意义。

由(19)式可知,在低压范围内,气体混合物在孔隙中的吸附选择性可通过计算各组分的可达面积和纵向Henry 系数来确定.
庚子(1900年)冬十二月,上海南洋公学演剧一次,南洋公学中院二班诸生,亦闻风踵效。是年适丁拳乱,因年假鱼暇。似取六君子及义和团事,编成新剧,就课堂试演,草草登场,诸多简陋,故知者绝鲜。[2]46对于南洋公学的本次演剧活动,鸿年在其《二十年来新剧变迁史》一文中有较为详细的记录:
2.2 纵向Henry 系数
在低压范围内,气体在基板表面的吸附量极低.与气-固原子间作用相比,气体原子间相互作用可忽略.在此情况下,气体分子数密度在狭缝中符合Boltzmann 分布:

式中,ρb为体相密度,β=1/(kBT),且kB为Boltzmann 常数,T为绝对温度.此外,气体还应满足Henry 定律[12],即吸附相中剩余吸附量正比于气体体相密度:
综上所述,辅导员在思想政治教育中的话语权是指辅导员开展大学生思想政治教育工作所具有的思想政治引领、观点表达、建议陈述等的资格和能力。它既是一项不容侵犯的权利,也是一项不容撼动的权力。
不再全然陌生,不再因偏见而更无知,不再充满猜疑甚至仇视,而是激赏对方的传统与文化,尊重各自的文明与希望……只有如此,当西方遇到东方,或者当东方遇到西方,才不会拒人千里之外,才可能拥抱如故友,才会缔造“高山流水遇知音”的佳话。而文化交流永远架设着不断交流的桥梁,话剧《茶馆》让美国观众“闻香下马”,堪为十多年前东西方交流的佐证,今天的“跨越太平洋——中国艺术节”,则体现了综合性、多样性、多社团、跨地区等特点,是中美文化交流领域资源共享、合作共赢的范例。

其中,KH为内禀Henry 系数,具有体积的量纲.Γex为狭缝中的剩余吸附量:

由于气体分子与固体原子间的体积排斥作用,气体分子的质心所能到达的空间将受到限制.因此,(9)式中Vacc表示气体分子质心所能到达的空间,即可达空间.鉴于图1(a)中各凸起沿x方向的无限延伸性,本文定义了纵向Henry 系数KL,并以此来量化纵向(x方向)单位长度内的剩余吸附量与体相密度的线性关系[27],即

为全面理解凸起对孔隙中气体的影响,图6 给出了在H=1.5 nm,D=0.34 nm 的情况下,H2的KL和随凸起间距w2的变化.图6(a)中的结果表明,当w1取不同值时,KL随w2的变大均呈增加趋势.这与图4(a)和图5(a)中的结果是一致的.图6(b)给出了当w1取不同值时,w2对的调制结果.图中结果表明,随w2的增大呈先升后降的变化趋势.该变化趋势是相邻凸起的吸附势在II-类区域内叠加程度发生变化所致.当w2较小时,增大w2使得凸起吸附势的强势范围从耗尽区域移入可达空间,并在II-类区域内叠加,从而增强气体分子在可达空间中的平均势能.当吸附势的极小由耗尽区域移入可达空间时,将达到峰值.然而,进一步增大w2会使得更大的弱势范围从耗尽区域移入可达空间,从而削弱了可达空间内的平均势能.此外,气体分子在狭缝中的可达空间随w2的增加而变大,这同样不利于可达空间内平均势能的增加.然而,w1的变大会抑制随w2的上升.当w1足够大时,随w2的增大呈单调下降趋势.

其中,Sacc=Vacc/Lx为狭缝中的气体分子在y-z平面内的可达面积.由此可见,KL具有面积的量纲,其物理意义为狭缝中气体的剩余吸附量在保持其纵向尺度不变的条件下转移至体相时,在y-z平面内所占据的面积.
2.3 等量吸附热

在Henry 范围内,气体分子的等量吸附热为[10]其中,R为气体常数,NA为Avogadro 常数.(12)式中RT为理想气体的动能贡献.不难发现,当T→∞时,气体分子的动能占绝对优势,从而导致其等量吸附热趋于极限值RT.因此,可达空间的体积Vacc应满足如下条件[28]:

结合图1(b)中Vsub(y,z)的算例结果,本文假设基板表面附近存在厚度为δ 的耗尽层,并以此来表征可达体积Vacc的边界,如图1(a)中凸起周围的蓝色虚线所示.需要说明的是,δ 的数值需通过求解(13)式得出.
2.4 二元气体混合物的吸附选择性
在多组分气体混合物的吸附中,固体材料对不同组分具有不同的吸附能力,进而表现出一定的吸附选择性.若考虑由A,B 两种组分组成的二元混合物气体,其吸附选择性可定义为[15]

结合(14)式,(17)式和(18)式,SA/B可进一步表示为

SA/B的计算可见附录B.(19)式中,为α 组分在y-z平面内的可达面积,其数值取决于基板形貌以及α 组分在凸起周围的耗尽层厚度δα.结合图1(a)不难得出,在粗糙狭缝(沿y轴)的空间周期λ 内,α 组分分子的可达面积为

其中,n和m为计数指标,分别用于区分基板上的第n个凸起和凸起上的第m层固体原子.Vm,0(y,z)的解析结果及相关计算可见附录A.根据(4)式对Vsub(y,z)的定义,下面首先对单一基板上相邻两个凸起之间的外势分布进行计算.计算中取w1=1.36 nm,w2=2.04 nm,M=3.图1(b)中的计算结果表明,Vsub(y,z)在y方向呈非均匀分布,且在凸起周围存在气体无法到达的耗尽层.
进行标贯试验189次,实测锤击数N’=52.0~127.0击,平均为87.0击;经杆长修正后N=36.4~88.9击,平均为61.1击。取样11组,共11件进行统计分析。建议地基承载力特征值的经验值fa=600kPa。
3 结果与讨论
为检验以上理论方法的有效性,首先计算了光滑石墨基板附近的Ne,Ar,Xr,Xe 等惰性气体的等量吸附热和Henry 系数随温度的变化,并与MC模拟结果[28]进行了对比.计算结果如图2 所示.计算中,石墨基板的外势由Steele 10-4-3 势描述,并取碳原子直径为σss=0.34 nm,体密度为ρst=114 nm-3,层间距Δ=0.3354 nm.气体分子间的相互作用由LJ 势描述,各种气体的LJ 参数均取与MC 模拟相同的数值,具体可见表 1.对比图2中的结果可见,对于Ne,Ar,Kr,Xe 等4 种气体,计算所得的等量吸附热和内禀Henry 系数KH均与相应的MC 模拟结果符合得极好.进一步,还计算了当T=298.15 K 时,受限于具有不同缝宽的石墨狭缝中的He,H2,Ar,N2,CH4,CO2等6 种气体的计算结果如图3 所示.图中对比结果表明,计算所得曲线与MC 模拟结果[10]完全符合.

图2 石墨表面上不同气体的(a)等量吸附热和(b)内禀Henry 系数 KH.线:本文结果;符号:MC 模拟结果[28].其中S为基板面积Fig.2.Isoteric heat of (a) adsorption and (b) inherent Henry constant KH of different gases on graphite surface.Lines:results of this work;symbols:results from MC simulations[28].S is the area of substrate.

表1 不同气体分子的LJ 模型参数Table 1.LJ model parameters of different gas molecular.

图3 T=298.15 K 时,光滑石墨狭缝中不同气体的 随缝宽H 的变化.线:本文结果;符号:MC 模拟结果[10]Fig.3.Dependence of on pore width H for different gases in smooth graphite slit pore at T=298.15 K.Lines:results of this work;symbols:results from MC simulations[10].
为了理解粗糙表面对气体的Henry 系数、等量吸附热和吸附选择性的影响,以下将进一步在Henry 范围内计算矩形波纹粗糙狭缝中气体的KL,和SA/B,并研究粗糙狭缝的几何形貌对以上特征的影响.需要说明的是,关于KL和的计算均以H2作为吸附质,而在SA/B的计算中,则以CO2/H2二元混合物为研究对象.此外,以下所有计算均取T=298.15 K.
3.1 凸起高度D 对KL和的影响
在光滑狭缝中,吸附相中气体的Henry 系数和与温度、气体种类以及气体分子与基板之间的相互作用强度有关.然而,对粗糙狭缝中的气体而言,除以上因素外,粗糙狭缝的几何形貌也会对气体的Henry 系数和产生显著的影响.因此,在w1=1.36 nm,且w2取不同值的情况下,分别计算了凸起高度D对H2气体的KL和的影响,计算结果如图4 所示.
[1]Halliday,M.A.K.Language as Social Semiotic:The Social Interpretation of Language and Meaning.London:Edward Arnold,1978:4-5.

图4 在w1=1.36 nm 和H=3.0 nm 情况下,凸起高度D对粗糙狭缝中H2的KL和的影响Fig.4.Effect of D on KL and of H2 in rough slit pore in the case of w1=1.36 nm and H=3.0 nm.
图4(a)中的结果表明,H2的KL-D曲线在整体上呈现先降后升的趋势.这可由以下竞争机制予以理解.一方面,较高的凸起可提供更强的吸附势,进而增强气体的吸附.另一方面,(20)式表明,对于给定的基板间距H,D的变大将增加凸起在孔隙中所占的空间,并压制气体分子的可达空间,进而不利于气体的吸附.当D较小时,新增固体原子所引起的吸附增量不足以弥补可达空间变小所导致的吸附量减少.此时,后者在竞争中占优势.相反,当D足够大时,前者将占据优势.对比各曲线不难发现,H2的KL的数值随w2的增大呈变大趋势,w2变大所引起的可达空间增加是其诱因之一.除此之外,任一凸起的吸附势范围均会与相邻凸起周围的耗尽层在II-类区域(如图1(a)示)内发生重叠.随着w2的变大,凸起吸附势中更大的强势范围将由耗尽区域移入可达空间的II-类区域,进而有益于气体在孔隙中的吸附.
3.2 凸起宽度w1对KL和的影响
图5(a)给出w1对H2的KL的影响.图中结果显示,气体的KL随w1的变大而单调增加.事实上,w1的增大不仅可增强同一基板上相邻两凸起之间的II-类区域内的势能,还可增强两基板上相对凸起之间的I-类区域内的势能.这与Kirkwood 叠加原理[34,35]是一致的.根据Kirkwood 叠加原理,粗糙狭缝中的性质可视为缝宽分别为H和H-2D的两个光滑狭缝中相应性质的权重平均.随着凸起宽度w1的变大,缝宽为H-2D的狭缝所占的权重随之变大.这相当于减小粗糙狭缝的有效缝宽,进而增强狭缝的吸附能力.此外,图5(a)中结果还表明,当w1较小时,KL-w1曲线斜率较大,这说明较窄的凸起对KL的调制作用更加显著.
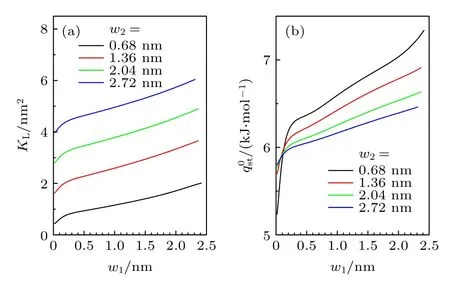
图5 在D=0.34 nm 和H=1.5 nm 情况下,凸起宽度w1对粗糙狭缝中H2的KL和的影响Fig.5.Effect of w1 on KL and of H2 in rough slit pore in the case of D=0.34 nm and H=1.5 nm.
图5(b)给出H2的随w1的变化.结合以上关于w1对KL的调控机制,不难理解图中随w1呈现增加趋势.然而,对比图5(b)中的各曲线可知,随w2的增加而变小.尽管w2的变大可减小凸起的吸附势与相邻凸起耗尽区域的重叠范围,但同时也增大了气体分子在狭缝中的可达空间.这将削弱气体分子的平均势能,并导致变小.
3.3 凸起间距w2对KL和的影响
其中,Lx为体系在x方向的尺度.结合(8)式和(10)式可进一步写为

图6 在D=0.34 nm 和H=1.5 nm 情况下,凸起间距w2对粗糙狭缝中H2的KL和的影响Fig.6.Effect of w2 on KL and of H2 in rough slit pore in the case of D=0.34 nm and H=1.5 nm.
3.4 基板间距H 对KL和的影响
除凸起的几何形貌外,基板间距H也可调制狭缝中的外势分布,进而影响气体的KL和.为此,本文在w1=w2=1.36 nm,且凸起高度分别取D=0,0.34,0.68,1.02 nm 的情况下,计算了H2的KL和随基板间距H的变化情况,相关结果如图7 所示.
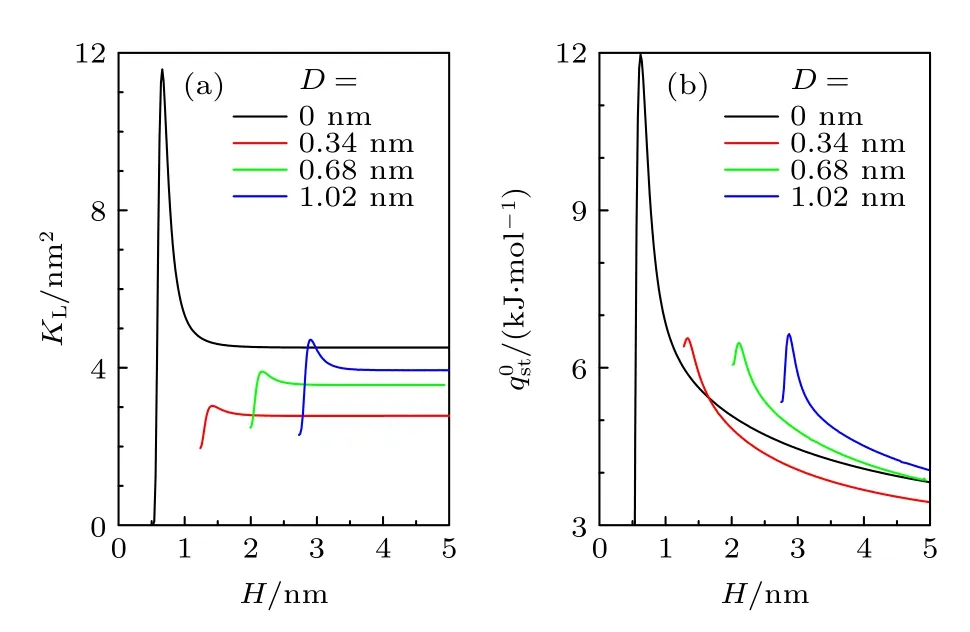
图7(a)给出KL随H的变化曲线.显然,粗糙狭缝的KL-H曲线与光滑狭缝情况均呈先升后降的变化趋势.当H较小时,两基板间的I-类区域因可达空间太小而无法容纳气体分子.当缝宽增至H-2(D+σsf)时,I-类区域内开始吸附气体.随着H的变大,吸附量将进一步增加并达到峰值.不难理解,该峰值应是由两基板吸附势的强势范围在I-类区域内的重叠所致.继续增大H,两基板吸附势的强势范围开始在I-类区域内分离.当H增至足够大时,两基板解耦,并不再有关联.此时,狭缝变成两个孤立的粗糙基板,且其吸附量趋于定值.图7(a)还表明,粗糙狭缝的KL小于光滑狭缝中的KL.这是由于基板上的凸起及其周围的耗尽区域减小了气体分子的可达空间,从而削弱了狭缝内总的吸附量.但是,随着凸起高度D的变大,狭缝的吸附能力将得以加强,正如图7(a)所示.
3.5 基板的几何形貌对SCO2/H2的影响
为方便起见,Vext(r)通常表达为来自上、下两个基板的外势贡献之和.由于图1(a)中体系的对称性,Vext(r)应与y,z有关.因此,粗糙孔隙中的外势可写为
图7(b)中的结果显示,在由粗糙基板构成的狭缝中,基板上的凸起同样对气体的-H曲线产生明显的调制作用.显然,每一条-H曲线均呈现峰值,且的峰值位置与图7(a)中KL的峰值位置一致.这同样与两基板吸附势的主体部分在I-类区域内的重叠程度有关.此外,对比不同D值情况下的-H曲线可知,在相同缝宽的情况下,气体的随D的变大而升高.这是由于随着凸起的升高,其吸附势中更大的弱势范围由I-类区域内的可达空间移入耗尽区域,从而导致可达空间内平均势能的增加.
首先,在w1=1.36 nm,H=3.0 nm,且w2取不同值时,计算了SCO2/H2随凸起高度D的变化.图8(a)中的结果显示,各SCO2/H2-D曲线均呈现先降后升的变化趋势.随着D的进一步增大,SCO2/H2的上升将趋于减缓.以上变化趋势是由两种气体在I-类区域内的适容性不同所致.当D较小时,I-类区域内的可达空间中只能容纳H2分子,而不能容纳CO2分子.此时,D的变大加剧了H2的吸附,并导致SCO2/H2的减小.然而,当I-类区域内的可达空间增至可容纳CO2时,D的进一步变大将加强CO2的竞争吸附优势,因为CO2与固体原子的相互作用强度更大.图8(a)中结果还表明,随着w2的变大,凸起对吸附选择性的影响被削弱.图8(b)给出在D=0.34 nm,H=1.5 nm,且w2取不同值时,SCO2/H2随凸起宽度w1的变化.计算结果表明,SCO2/H2随w1呈先升后降的变化趋势,且SCO2/H2的升、降幅度均随w2的变大而变弱.根据Kirkwood 叠加原理,w1的变大导致宽度为H-2D的光滑狭缝所占的权重变大,从而增强了狭缝的吸附能力.其中,狭缝对CO2的吸附增强应更显著.但是,当w1足够大时,w1的变大将增强狭缝对H2的吸附,进而导致SCO2/H2的减小.这是由狭缝中气体的混合熵增加所决定的.此外,随着w2的变大,宽度为H的光滑狭缝所占的权重增加,导致上述的调控机制被削弱.

图8 不同条件下,基板几何形貌对吸附选择性SCO2/H2的影响 (a) w1=1.36 nm,H=3.0 nm 时,D 对SCO2/H2的影响;(b) D=0.34 nm,H=1.5 nm 时,w1 对SCO2/H2的影响;(c) D=0.34 nm,H=1.5 nm 时,w2 对SCO2/H2的影响Fig.8.Effect of geometric morphology on the selectivity SCO2/H2 in rough slit pore:(a) Effect of D on SCO2/H2 with w1=1.36 nm and H=3.0 nm;(b) effect of w1 on SCO2/H2 with D=0.34 nm and H=1.5 nm;(c) effect of w2 on SCO2/H2 with D=0.34 nm and H=1.5 nm.
图8(c)给出在D=0.34 nm,H=1.5 nm,且w1取不同值时,SCO2/H2随凸起间距w2的变化.显然,当w2较小时,SCO2/H2随w2的增大而变大.事实上,若w2很小,相邻两凸起之间II-类区域内的可达空间因无法容纳CO2分子而被H2分子占据.此时w2的变大使得CO2分子进入II-类区域的概率变大,从而导致SCO2/H2变大.然而,随着w2的进一步变大,狭缝中II-类区域内的平均势能被削弱,进而使得SCO2/H2随w2的增大而减小.
3.6 基板间距H 对SCO2/H2的影响
除粗糙基板的几何形貌外,两基板的间距H也会对SCO2/H2产生一定的影响.本文在w1=w2=1.36 nm,且凸起高度D取不同值的情况下,计算了基板间距H对SCO2/H2的影响.计算结果如图9所示.

图9 w1=w2=1.36 nm 的情况下,基板间距H 对SCO2/H2的影响Fig.9.Effect of H on selectivity SCO2/H2 of CO2/H2 mixture confined in rough slit pore with w1=w2=1.36 nm.
图9 中的结果表明,光滑狭缝的SCO2/H2-H曲线呈先升后降的变化趋势,且下降趋势随H的变大而逐渐变缓.曲线中峰值可归因于不同类型的分子在狭缝中可达空间内的适容性的区别.同样,粗糙狭缝中CO2和H2在I-类区域内可达空间中的适容性的差异也将导致其SCO2/H2-H曲线呈现明显的峰值.相比之下,粗糙基板中的SCO2/H2随H的衰减更加显著.而且,当H足够大时,粗糙基板中的SCO2/H2明显小于光滑狭缝中的SCO2/H2.这说明在较宽的狭缝中,粗糙基板上的凸起可压制CO2在竞争吸附中的优势.
3.7 三角形和半圆形凸起对吸附性质的影响
在以上的计算中,粗糙表面均被模化为矩形波纹形状.计算结果表明,粗糙表面的几何形貌可在很大程度上影响和调制其附近气体的吸附性质.然而,实际固体材料的粗糙表面可能具有不同的几何形貌,进而导致其对吸附性质的影响发生变化.因此,为了更为全面地理解粗糙表面附近的气体吸附,下面分别计算并研究具有如下两种不同形状凸起的粗糙狭缝对气体吸附性质的影响:1)底宽为w1,高为D等腰三角形凸起;2)半径为R的半圆形凸起.计算结果如图10 所示.
急性期治疗的手段包括非手术疗法及手术方法。非手术疗法主要包括静脉溶栓、药物抗凝、置入静脉滤器、弹力袜应用;手术方法包括经导管溶栓、经导管取栓、静脉切开取栓。发病时间短且有良好手术条件患者,建议行手术治疗溶栓或取栓治疗;无手术条件及溶栓条件时,则需要充分药物抗凝治疗,可以预防深静脉血栓严重并发症肺栓塞的发生,常规抗凝药物有普通肝素、低分子肝素、华法令等,研究显示新药达比加群酯治疗儿童血栓效果好[15] ,不同患者更多口服药物如利伐沙班、阿哌沙班等可以选择应用达到良好效果[16-17],根据发病不同时期及病情严重程度适宜选择不同药物及使用疗程。
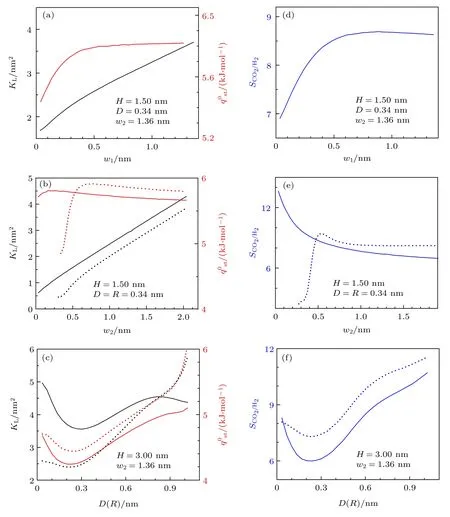
图10 (a)—(c) 三角形和半圆形凸起对狭缝中H2的KL和的影响.图中,黑线和红线分别为KL和的结果,实线和虚线分别为三角形凸起和半圆形凸起情况下的结果.(d)—(f)三角形和半圆形凸起对对SCO2/H2的影响.图中,实线和虚线分别为三角形凸起和半圆形凸起情况下的结果.需要说明的是,在图(b)和图(e)中,三角形凸起取w1=0.68 nm,而在图(c)和图(f)中,三角形凸起取w1=1.36 nmFig.10.(a)–(c) Effect of geometry on KL and of H2 in rough slit pore with triangular and semicircular corrugated substrates.In these figures,black lines and red lines correspond to results for KL and ,respectively.In addition,solid and dashed lines stand for results of triangular and semicircular condition,respectively.(d)–(f) Effect of geometry on selectivity SCO2/H2 of CO2/H2 mixture in rough slit pore with triangular and semicircular corrugated substrates.In these figures,solid and dashed lines stand for results of triangular and semicircular condition,respectively.It should be noted that in panels (b) and (e),w1=0.68 nm is set for the triangular corrugated substrate,while in panels (c) and (f),it is set as w1=1.36 nm.
图10(a)给出了H=1.50 nm,D=0.34 nm和w2=1.36 nm 的情况下,具有三角形凸起的狭缝中H2的KL和随w1的变化.图中结果表明,对于给定的H,D,w2,体系的KL和均随w1的变大呈增大趋势.这与图5 中矩形凸起狭缝中结果的变化趋势一致.然而,与图5 中同条件下的结果相比,三角形凸起狭缝的KL比矩形凸起狭缝的KL更大,但比矩形凸起狭缝的更小.事实上,这可由以下竞争机制予以理解:在给定H,D,w2时,三角形凸起狭缝中的气体分子比其在矩形凸起狭缝中具有更大的可达空间,这有利于气体分子的吸附;另一方面,与矩形凸起相比,三角形凸起提供的吸附势相对较弱,进而不利于气体分子的吸附.前者的优势地位导致三角形凸起狭缝的KL大于矩形凸起狭缝中的结果.同时,三角形凸起狭缝中较大的可达空间和较弱的吸附势协同导致其中气体分子的平均势能小于同等条件下矩形凸起狭缝的结果.
当然好的学习习惯和学习方法是必不可少的。好的学习方法和习惯可以帮助学生更快的接收知识,能够更快的弥补之前学习的不足。
实验组患者的治疗总有效率(92.31%)明显高于对照组患者的治疗总有效率(74.36%),组间数据比较差异有统计学意义(P<0.05)。见表1.
图10(c)所示为H=3.00 nm和w2=1.36 nm的情况下,三角形和半圆形凸起狭缝中H2的KL和随凸起高度的变化.其中,三角形凸起取w1=1.36 nm.显然,图10(c)中三角形凸起狭缝的结果与图4 中的矩形凸起狭缝的结果具有相同的变化趋势.但是,其KL大于矩形凸起狭缝在同条件下的值,且其小于矩形凸起狭缝在同条件下的值.由于半圆形凸起的底部宽度随其半径而变化,故图10(c)中三角形和半圆形凸起狭缝之间的结果不具可比性.然而,半圆形凸起狭缝的结果表明,其KL和随凸起高度的变化趋势与矩形凸起狭缝的情况一致.
企业信息管理系统的应用和发展,以所使用的网络为特征,可以分为生产局域网应用阶段、企业有线网络阶段,以及企业无线移动网络应用阶段。
图10(d)—(f)为不同的条件下三角形和半圆形凸起狭缝中CO2/H2二元混合物的吸附选择性.计算中,图10(d)和图10(a),图10(e)和图10(b),图10(f)和图10(c)分别采用了相同的凸起几何参数.从图8 可以看出,CO2与固体之间较强的作用强度使得其在与H2的吸附竞争中占据优势.相比于矩形凸起狭缝,三角形和半圆形凸起对气体分子的吸附势相对较弱.由此不难理解图10(d)—(f)中体系的SCO2/H2小于矩形凸起狭缝在同条件下的结果.此外,图10(e)中三角形凸起和半圆形凸起情况之间的结果对比还表明,当D=R且w1=2R时,在三角形凸起狭缝中的SCO2/H2小于半圆形凸起狭缝中的SCO2/H2.这是由于与半圆形凸起狭缝相比,三角形凸起狭缝中的吸附势更弱,从而削弱了CO2在狭缝中的吸附优势.
4 结论
为研究粗糙孔隙中气体的吸附特征,本文采用矩形波纹粗糙基板构造粗糙狭缝模型,计算了狭缝中的外势分布.基于该模型,在Henry 范围内研究了粗糙基板上凸起的几何形貌对H2的纵向Henry系数、等量吸附热等性质的影响和调制作用.研究结果表明,粗糙基板上凸起的高度、宽度、间距以及两基板间距等几何因素均可对上述性质产生显著的影响和调制作用.其中,各凸起的吸附势在气体分子可达空间内的关联起着重要的调制作用.进一步在Henry 范围内计算了CO2/H2二元混合物气体在粗糙狭缝中的吸附选择性.研究表明,吸附选择性与各组分在孔隙中的可达空间和纵向Henry 系数均有关系.研究结果表明,粗糙基板上凸起的几何形貌和基板间距均可显著地调制CO2/H2混合物的吸附选择性.此外,为了更全面地理解凸起的几何形状对气体吸附性质的影响,还进一步计算并研究了具有三角形和半圆形凸起的粗糙狭缝中气体的Henry 系数、等量吸附热和吸附选择性.以上研究结果有望为功能材料的设计与表征提供有益线索,并可为碳封存、储氢等领域的实验研究提供可靠的理论依据.
附录A 关于Vm,0(y,z)的计算
下面计算粗糙基板上第0 个凸起中的第m层固体原子施于气体分子的外势Vm,0(y,z).如正文中所述,气体分子和固体原子之间的相互作用由LJ 势来描述.因此,Vm,0(y,z)可分解为吸引部分和排斥部分的贡献,即
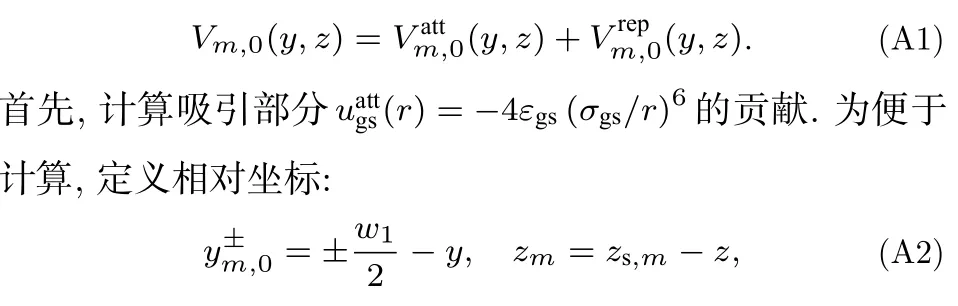
其中,zs,m=mΔ为第m层固体原子的z坐标.基于此,气体分子与第0 个凸起中第m层固体原子之间的吸引作用的贡献可通过对该层内所有固体原子的积分来得出
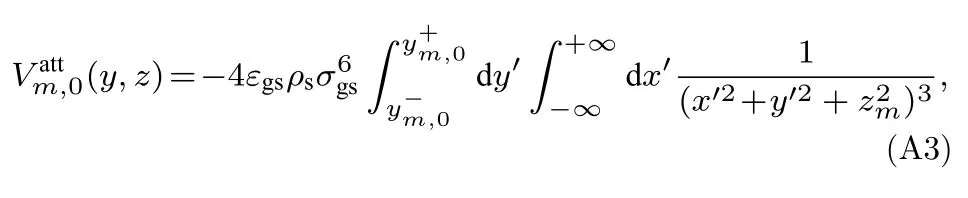
这里,ρs为每层中固体原子的面密度.本文在计算中取ρs=38.2 nm-2.利用已知结果
(3) 处治方案需要因症施策、综合处治:凹岩腔嵌补、裂缝灌缝等结构修复为根本,仰孔排水、滑坡体外截排水等排水、控水为关键,清渣、削坡等减载为辅助,桥梁基础加固为保障。
5.给仔猪注射三九克痢、庆大霉素、海达注射液,每天2次。同时注意给仔猪补液,可用10%安钠咖5 ml、2.5%维生素B 3 ml、10%维生素C5 ml、1%硫酸阿托品2 ml、5%葡萄糖100 ml、生理盐水85 ml,混合。将混合液加温至39℃,按每头仔猪每日用5 ml的量,进行腹腔注射。

可得

计算(A5)式中的积分,并进一步记作辅助函数Φ6(y,z):

其中,辅助函数Φ12(y,z)为

综合(A1)式,(A7)式和(A8)式,Vm,0(y,z)最终可表示为

附录B 关于SA/B的计算
由正文可知,对由A,B 两种组分组成的混合物气体,其吸附选择性可定义为


