基于粒子群优化算法的相变换热器动态仿真研究

王晓霞，麻宏强，宋兴鹏

(1.山西工程科技职业大学 设备工程学院，山西 太原 030600； 2.华东交通大学 土木建筑学院，江西 南昌 330013； 3.兰州理工大学 土木工程学院，甘肃 兰州 730050)

引 言

翅片管式相变换热器是含硫烟气余热相变回收系统中关键的换热设备[1]，高温含硫烟气与低温换热工质在其中交换热量，同时管内工质发生相态变化，换热过程较为复杂。

在余热回收系统中常见的换热设备有套管式换热器、板式换热器和管壳式换热器等[2-3]。目前，常用的建模方法有机理建模和实验建模，机理模型有非常明确的物理意义，但是对于某些复杂对象难以列写机理方程，实验建模又称为系统辨识，但依赖大量的数据。Gao Tianyi等[4]通过机理建模方法研究了无相变叉流式换热器动态数学模型，列写了壁面和流体之间无量纲能量守恒方程。Emanuel Feru等[5]搭建了重型柴油机能量回收系统中的两相换热器动态数学模型。目前，对换热器的大部分研究主要集中在静态、无相变的板式换热器和管壳式换热器[3，6-9]的机理模型。而烟气余热相变回收系统烟气换热器类型属于翅片管式叉流相变换热器，相变换热是一个动态过程[10]，换热过程比较复杂[11]，已有模型难以借鉴，需要选择适当的建模方法重新建立烟气换热器动态数学模型。

常见的PID控制器参数整定方法有Ziegler-Nichols整定法、临界比例度法和衰减曲线法等，在实际的优化问题中，往往难以整定出最优参数，因为每个参数的稳定裕度取决于其他值，同时还耗费大量人力资源[12]。粒子群优化(Particle Swarm Optimization,PSO)算法是近年迅速发展起来的一种智能优化算法[13]。该算法是基于群体进行优化的方法，先将系统初始化为一组随机解，通过迭代搜索最优值。粒子群优化算法优点在于其原理简单，更易实现，需要调整的参数较少，因此粒子群优化算法被广泛应用于控制器参数寻优[14-17]。

本文建立了相变换热器动态数学方程，运用频域分析及拉氏变换的求解方法，基于辨识理论得到烟气换热器具体动态模型参数，并使用实验数据验证该模型的适用性，采用单位阶跃信号和正弦波信号作为参考信号进行仿真分析，分析其过渡过程品质和跟踪性能。

1 动态模型简化

1.1 基本假设及微元段的选取

常见的相变换热器有板翅式换热器和翅片管式换热器等，以翅片管式烟气换热器作为研究对象，其简化几何模型如图1所示。

图1 烟气换热器实物

对换热器作如下基本假设：

(1)换热器的内部无化学反应，与外部环境不发生热交换；

(2)管程流体不可压缩，且以活塞流的形式流过换热器；

(3)壳程内流体同一截面上的各点温度均相同，即不考虑流体沿径向传热；但考虑流体的轴向扩散效应，忽略流体入口效应；

(4)壁面热阻和污垢热阻均与管壳侧对流换热热阻结合在一起；

(5)管程LiBr水溶液均是饱和溶液。

沿换热器烟气流动方向取微元长度为Δx微元体，如图2所示。对壳程、管程及壳管间做微观能量分析，建立能量守恒微分方程，x轴方向平行于烟气流动方向。假设烟气换热器中的管程是纵向的，且所有并联金属管可等效成一根传热管，微元体中的管程可等效成一根换热管，如图3所示。

图2 翅片管式烟气换热器简化示意图

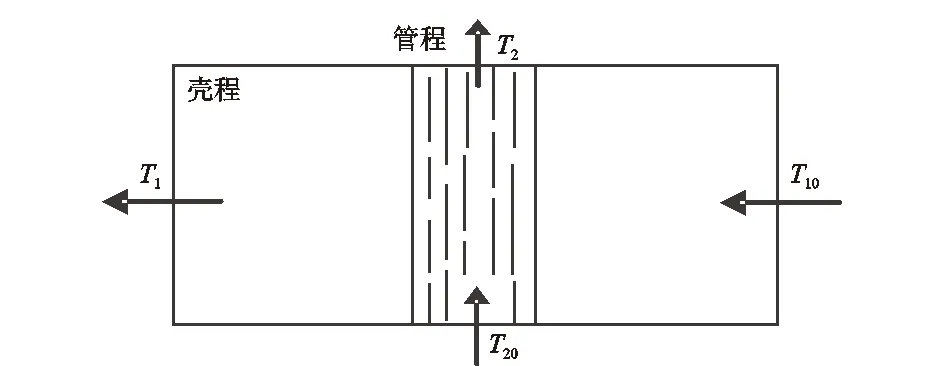
图3 换热器微元体示意图

1.2 微元方程

基于假设(1)—(5)，建立微元体动态数学方程。

壳程：

(1)

式中：ρ1为烟气密度，kg/Nm3；c1为烟气比热容，kJ/(kg·℃)；T1为烟气温度，℃；A为烟气换热器壳程横截面积，m2；λ为烟气的导热系数，W/(m·K)；u1为烟气流速，m/s；qV为单位体积壳管间的换热量，kJ/m3。

管程：

(2)

式中：m20为烟气换热器进口处LiBr溶液的总质量流量，kg/s；ε为烟气换热器管程LiBr溶液中水蒸气的质量分数；c2、c2＇分别为烟气换热器出口及进口处LiBr溶液的比热容，kJ/(kg·℃)；T2为LiBr溶液温度，℃；γ为饱和水蒸气的汽化潜热，kJ/kg；c为水的比热容，kJ/(kg·℃)；L为烟气换热器壳程长度，m；T20为烟气换热器LiBr溶液进口温度，℃。

壳管间换热：

(3)

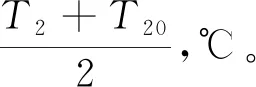
1.3 方程求解

在烟气余热回收工艺中，避免低温腐蚀现象要求合理控制换热器烟气出口温度，而不是沿壳程的温度分布，换热器烟气出口温度的描述可简化为常微分方程[18]。为了简化求解，忽略初始状态的影响，在零初始条件下，对式(1)和式(2)的时间项进行拉氏变换：

(4)

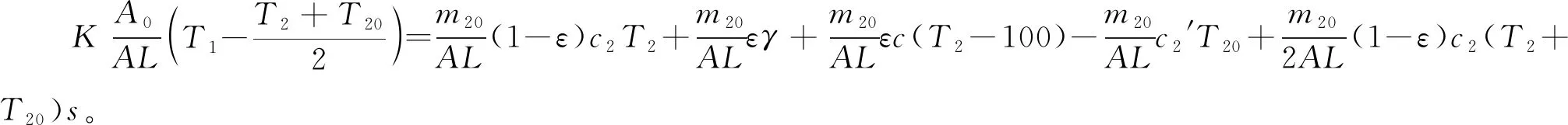
(5)

令

(6)

式(5)可化简为

(7)

联立式(4)和式(7)得

(8)

假设烟气换热器中每一根竖管中的汽化量相同，即每一根竖管的吸热量相同，每一根竖管出口溶液的干度相同，烟气沿流动方向温度呈线性变化；同时传热过程中的信号大多都是低频的，即s→0。由此进行简化，得到关于烟气温度T1的一阶常微分方程：

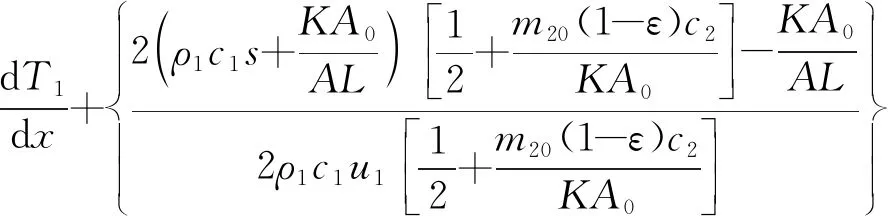
(9)

令

(10)

式(9)可化简为

(11)

边界条件

T1|x=0=T10。

(12)

求解微分方程得

(13)

根据物理意义对α、β进行简化，得

(14)

换热器管程溶液出口干度

(15)

基于假设(7)，因为设计干度ε相比于m20很小，则m20(1-ε)≈m20，即烟气换热器烟气动态数学表达式为

(16)

(17)

烟气换热器的动态数学模型化简为

(18)

其中，模型系数的具体参数表达式见表1。

表1 模型参数

依据式(18)，可以得出：换热器烟气出口温度T1与烟气进口温度T10及溴化锂溶液进口温度T20有关，故可将溴化锂溶液进口温度T20看作系统的输入量，烟气进口温度T10看作影响系统输出量T1的干扰量。在T10和T20项对应的模型表达式中系数B～I随着系统参数A、L、u1、m20、ρ1、c1、c2、c2＇变化而变化，即该换热器动态数学模型随着工艺参数的变化而变化。

1.4 参数辨识

搭建烟气余热相变回收实验台，使用烟气余热相变回收动态响应实验时域数据，基于系统辨识理论和过程传递函数模型(process model)的辨识方法，辨识得到相变换热器动态数学模型具体参数

(19)

2 模型验证

相变换热器动态数学模型随工艺参数和工况条件的变化而变化，对式(19)的适用性进行验证，改变动态响应实验中送风机频率和溴化锂水溶液循环泵频率，即改变换热器壳程烟气流速u1和管程溴化锂水溶液流量m20，取动态响应实验中4组工况数据验证，对实验数据与对应辨识模型输出进行比较，结果如图4所示。

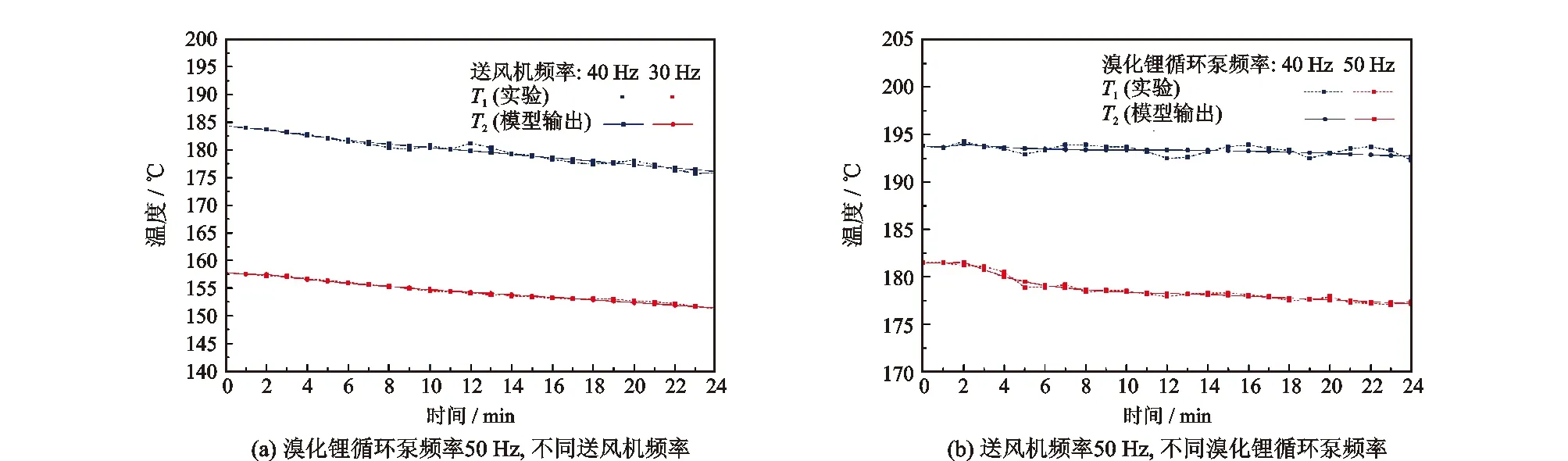
图4 实验输出数据与仿真模型输出结果

从图4中可以看出，4种工况下动态模型输出结果与实验数据的最大相对误差分别为0.29%、0.76%、0.32%和1.21%，均不超过±1.5%，因此该动态模型具有较高可信度，能够模拟烟气换热器的实际换热，可用于搭建控制仿真模型。

3 仿真分析

3.1 粒子群优化算法

PID控制器对于一般控制系统具有原理简单、适应性好、鲁棒性强等特点。通常评价控制系统的动态性能指标是过渡过程的品质指标，如调节时间、超调量等，PID控制器的输出信号为

(20)

式中：Kp为比例系数；Ti为积分时间常数；τ为微分时间常数。工程中常用的PID控制器参数整定方法主要有Ziegler-Nichols整定法、临界比例度法和衰减曲线法等，这些方法的共同特点是通过试验然后按照工程经验公式对控制器参数进行整定。当换热器工艺参数改变后，换热器数学模型随之变化，控制器参数不再适应，重新整定新的控制器参数又需要消耗大量人力资源。

粒子群优化算法(PSO)是学者Kennedy和Eberhart首次提出的一种新型的仿生算法，PSO因其需要调节的参数少，具有逻辑简单且易于实现的优点，因此越来越多地被应用于参数优化等领域。按照追随当前最优粒子的原理，粒子x将按

vij(t+1)=wvij(t)+c1r1j(t)[pij(t)-xij(t)]+

c2r2j(t)[pij(t)-xij(t)]，

(21)

xij(t+1)=xij(t)+vij(t)

(22)

改变自己的速度和位置。其中，j=1，2，…，D；i=1，2，…，M；w为惯性权重因子；M为种群数量；t为当前进化代数；r1、r2为分布于[0，1]的随机数；c1、c2为加速常数。

3.2 基于粒子群算法的控制器参数优化性能分析

单位阶跃信号是判断控制系统瞬态响应特性最常用信号，基于不同整定方法的翅片管式相变换热器出口温度PID控制器的单位阶跃响应如图5所示。控制器参数及阶跃响应性能指标参数见表2。

表2 控制器参数及阶跃响应性能指标参数

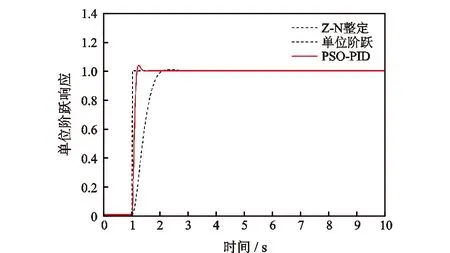
图5 基于粒子群算法整定控制器参数的单位阶跃响应

从图5中可以看出，基于粒子群算法的整定方法上升时间和调节时间明显少于经典的Z-N整定法，上升时间为1.18 s，同时在1.34 s的最短时间内实现了温度响应的稳定，说明该方法在翅片管式相变换热器出口温度PID控制器参数整定中速度快且稳定，同时可代替人工繁琐的整定过程，具有良好的工程实用性和选择性。

为了验证系统的跟踪特性，采用单位正弦波作为输入信号。温度响应和参考信号如图6所示。基于粒子群优化算法整定PID控制器参数的输入参考信号与输出之间存在0.08 s的滞后时间，与输入信号具有相同的频率。结果表明，基于粒子群算法的整定方法具有良好的跟踪性能。

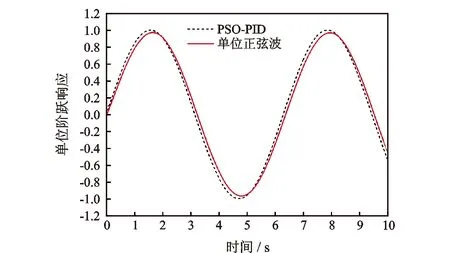
图6 基于粒子群优化算法整定控制器参数的单位正弦波响应

4 结 论

(1)基于相变换热器几何模型和物理模型的基本假设，取其微元体并建立微元动态数学微分方程；运用频域分析及拉氏变换方法，根据物理意义对其简化，求解得到相变换热器三阶动态模型；

(2)运用时域数据，基于辨识理论得到动态数学模型具体参数，确定了相变换热器动态模型；使用实验数据验证模型适用性，模型输出结果和实验数据的相对误差均能够保持在±1.5%以内；对翅片管式相变换热器性能分析具有一定参考价值和指导意义。

(3)对翅片管式相变换热器动态数学模型进行仿真分析，采用单位阶跃信号和正弦波信号作为参考信号，基于粒子群优化算法的PID控制器参数整定方法，其单位阶跃响应上升时间和调节时间分别为1.18 s和1.34 s，具有良好的过渡过程品质和跟踪性能。