一种高效的任意梯度掺杂实现方法及其应用

李全泽，黄尊恺，田犁，祝永新，汪辉，封松林

（1 中国科学院 上海高等研究院，上海 201210）

（2 中国科学院大学，北京 100049）

0 引言

在过去的二十年间，图像传感器技术的研究热度和市场需求增长迅速，图像传感芯片的生产工艺正在从电荷耦合元件（Charge Coupled Device，CCD）向互补金属氧化物半导体（Complementary Metal Oxide Semiconductor，CMOS）过渡。由于二者技术难点存在许多不同，很多研究方向都已经改变，但提高像素内部电子的传输效率一直是最重要的研究方向之一。而CMOS 图像传感器（CMOS Image Sensor，CIS）像素设计的关键点就在于光电二极管（Photodiode，PD）内部光生电荷的转移，特别是在需要大尺寸像素的应用场景中，如医疗影像［1］、天文成像等，需要高速地检测到有限的信号，对光电二极管内电荷的传输效率要求极高［2］。

电荷传输是受多种因素影响的复杂过程，在半导体物理中通常将其分解为漂移运动和扩散运动进行研究［3-4］。在CCD 结构为主导的发展期间，LEE 等对其内部电荷传输的过程进行了分析汇总［5-7］，而构成CCD基本单元的MOS（Mental-Oxide-Semiconductor）结构与PD 结构具有高度一致性，将二者类比分析后可得出结论，外加电场可提高光电二极管内部电荷的转移速度；在没有电场的条件下，扩散运动占主导地位，电荷传输的时间和传输距离的平方成反比。根据这一性质，可给出扩散系数D的定义［8］。关于提升光电二极管中的电荷传输速度的解决方案，主要可以分为两类：添加外部偏置电场或内部制造电势梯度。添加外部电场的方法［9］，应用场景有较大的局限性［10-11］，随着器件尺寸减小，实现难度呈指数增大，且会提升降低像素间串扰的成本。在内部制造电势梯度的方法又可以分为设计特殊的二极管形状和制造非均匀掺杂分布两个方向。前者最近提出的实现方法［12］虽然性能表现良好，但实现步骤较早期的方法［13-15］愈发复杂，此外，此类方法形成内部电势梯度的同时无形降低了填充因子，本质上是牺牲空间利用率提升传输效率。后者目前主流的方法［16-20］是通过多次不同剂量的注入形成浓度梯度，相较于传统工艺的一次注入，一方面制造成本有所提高；另一方面，多次离子注入会增加晶格缺陷产生的风险，导致芯片良率降低，虽然已经提出了多次快速热退火等弥补方案，但这会增加工艺流程的复杂性。此外，上述方法只有部分存在定性的概述，缺乏完整的理论分析，尤其是定量的分析方法。这导致在提升器件性能的研究过程中，需要耗费大量的时间来调整参数，且对最终的结果无法有相对精确的预测。当转变应用场景或者改变器件尺寸时，工艺上的注入能量、注入剂量，扩散时间等参数无法根据先前的实验结果快速调整。因此，需要一种可以定量分析整个掺杂过程的方法，提高梯度掺杂设计和研究工作的效率。

本文对整个掺杂的物理过程进行了建模，提出了一种可以在光电二极管中，高效的制造任意梯度掺杂分布的方法。相较于传统方法，该方法提出了一套可以定量的分析光电二极管内任意两个时刻的分布变化的分析理论，针对器件尺寸变化等情况，可以快速且相对精确的重新确定扩散时间等工艺参数，在相关工艺参数确定后，能精确的预测最终的分布结果。此外，本文将此方法应用在CIS 像素中，设计了具有梯度掺杂的PD 收集区，相较于传统工艺，极大地提高了光生电荷的转移效率。

1 相关理论分析

本节针对整个掺杂工艺流程做了如下假设：整个掺杂工艺的流程可视为在无外部电场环境下进行；除了目标掺杂区域外的其他区域视为不可穿透的扩散阻挡层；掺杂区域晶格均匀分布；忽略边界处的缺陷和相关边缘电场效应；扩散系数D不随空间位置的改变而变化。基于上述假设对整个掺杂过程建模，将其分解为离子注入和热扩散两个阶段。

1.1 离子注入阶段

离子注入的完成时间相对较短，注入离子在硅片内会发生散射以及受到硅原子核外电子的库伦力，导致杂质离子的实际运动过程（图1）难以预测。但对于整体的分布而言，杂质离子的运动路线并不重要，重要的是其在硅片内纵向分布范围的极限，将离子注入硅片内部后的散射距离在纵向投影，在注入能量确定后，杂质离子在硅片中纵向上的平均投影射程RA相应也就确定了，RA的值由杂质离子和硅的性质决定，该点水平切向对应的浓度记为C0，可与注入浓度近似。离子注入结束后，RA附近纵向的浓度分布可近似为高斯函数形式。将纵向一点与平均投影射程RA的投影距离记为ΔRA，纵向的浓度分布Cy可由式（1）得到。即在纵向投影上，RA两边注入离子浓度对称的下降。

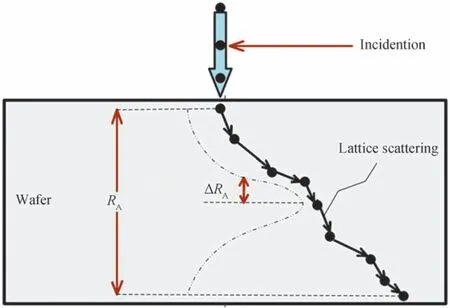
图1 注入离子在硅片内运动过程示意Fig.1 Schematic of movement process of implanted ions in silicon wafer

1.2 热扩散阶段

将离子注入阶段结束的时刻作为热扩散阶段开始的时刻，把两个过程联系起来，由于假设不存在外力干扰，扩散源唯一且与时间无关。在杂质扩散的过程中，借助菲克第二定律［21］，可以得到传输通量和浓度梯度之间的关系。根据1.1 节的分析可以确定扩散方程的初始条件，因此可以对整个扩散过程建立齐次微分方程，表示为

式中，C为杂质浓度，x为横向坐标，t为扩散时间，假设某扩散源的注入位置的横向坐标为x0，求解式（2）可以得到掺杂分布的状态密度函数，即

对于任意的分布函数C（x），可借用狄拉克函数δ（x）将其在定义域上展开为积分形式，表示为

式中，y是积分变量，无实际意义，式（4）中的狄拉克函数可在邻域展开成高斯函数形式，表示为

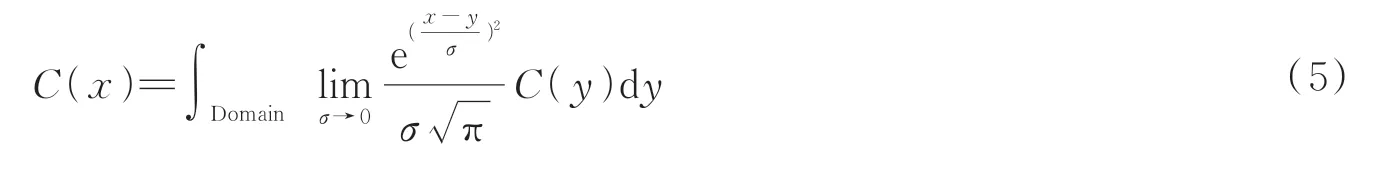
式中，σ是一个高阶无穷小量。将式（5）与式（3）进行对比，可发现当趋近于无穷小时，两式具有高度的一致性，即对于任意的分布函数C（x），可将其拆分为多个形如式（3）函数的累加的级数。

到此，式（6）中的每一个参数都有了实际对应的物理意义，为了得到与初始浓度C0相关的掺杂分布函数，可以使用具有n个不同间距开口的掩膜版，进行一次离子注入，控制扩散时间，等效得到前文分析的累加级数。每一个开口的特征长度记为l，定义为

而第i个开口的宽度定义为

所以式（6）在实际工艺时计算的累加级数形式为

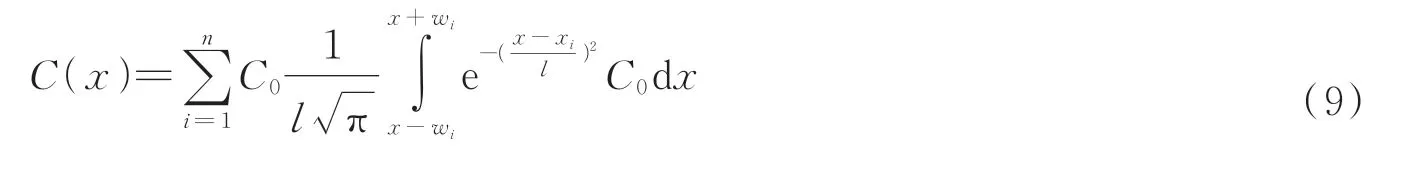
通过上述分析，证明了理论上可以通过一次离子注入和扩散制造任意的掺杂分布函数，图2为整个过程的示意图。

图2 离子注入与扩散示意Fig.2 Schematic of ion implantation and diffusion

2 模拟计算

本节以制造线性梯度分布函数为例，应用第1 节中的理论进行设计，假定扩散范围为0 到100 μm，掩膜开口数量n为10，目标分布函数可表示为

掩膜开口的设计方案如表1。将掩膜开口方案对应的参数代入式（9），计算得到每个开口单独作为扩散源在扩散结束后的分布函数，将所有的函数累加后的模拟计算分布与理论目标分布做对比，对比结果如图3（a），实线为所有开口分布累加后的模拟计算分布，虚线为理论目标分布。将一维的线性分布拓展到二维平面，模拟计算后的结果如图3（b）。

表1 掩膜开口中心与宽度设计方案Table 1 Design scheme of mask opening center and width

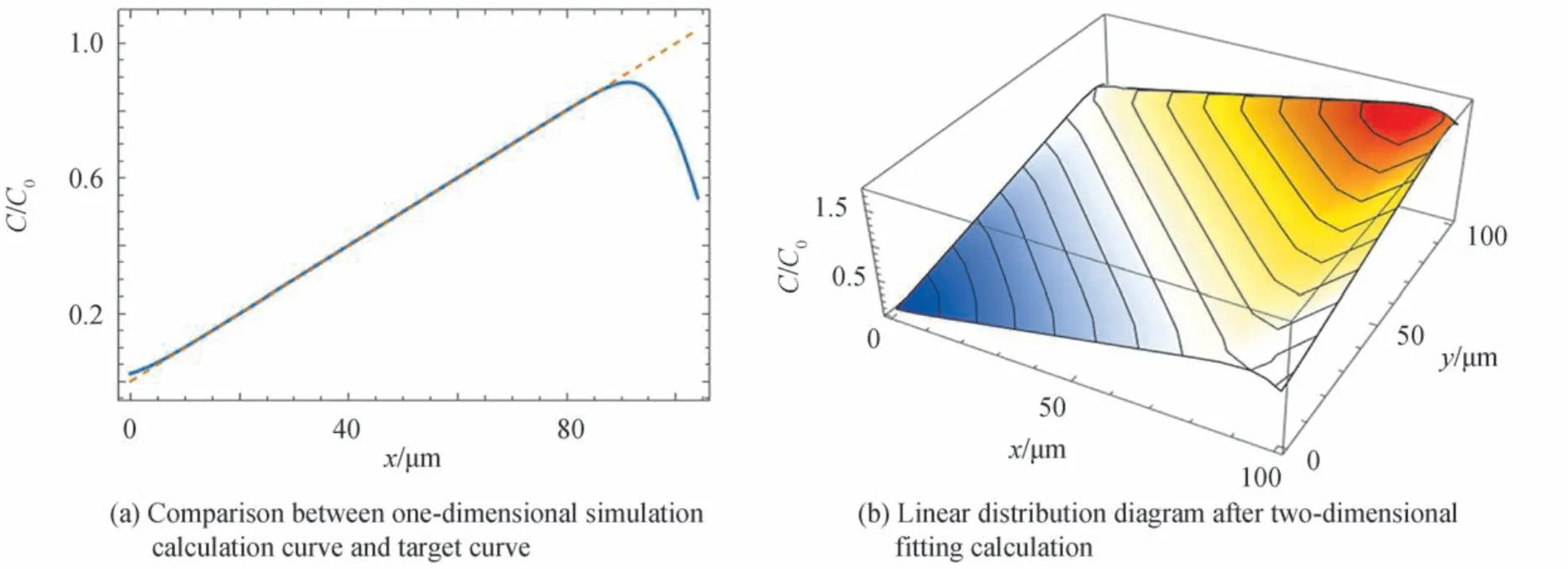
图3 一维和二维模拟计算结果Fig.3 One dimensional and two-dimensional simulation results

3 仿真验证

3.1 在硅衬底上制造梯度掺杂

在100 μm 的P 型硅衬底上，注入硼杂质，设计线性的掺杂分布，掩膜开口数量定为10 个，截取中间部分时间节点的浓度分布图观察，结果如图4（a）。在距表面1 μm 处分别截取不同时刻的横向分布，其结果对比如图4（b）。

图4 不同时刻衬底掺杂区域的状态Fig.4 The state of the substrate doping region at different times

随着扩散时间的增加，掺杂分布函数逐渐趋近于线性分布。由此可以证明第1 节提出的理论在实际工艺流程中是可行的，最佳的扩散时间由特征长度L与扩散系数计算得到，而当扩散时间进一步延长后，以线性分布为例，掺杂分布函数会趋向于完全线性，但固定切面的浓度梯度即线性函数斜率会逐渐减小。如果扩散时间延伸至无限长，理论上最终所有的设计都会变成均匀分布。

3.2 在单个CMOS 像素内制造梯度掺杂

在实际的芯片生产流程中，除了对光电二极管的目标区域进行梯度掺杂外，往往还需要其他多次离子注入和退火等对掺杂分布有影响的步骤。由于第1 节提出的理论对各个参数的计算十分精确，为了证明可以将其应用在实际生产环境中，需要将该理论融入到完整的工艺流程中。本节将介绍把设计梯度掺杂分布的理论应用到完整器件的方法，选择的器件为前照式（Front-Side Illuminated，FSI）CMOS 单像素图像传感器［22-24］。如图5所示，整个制造流程主要包含以下几个步骤：

图5 FSI 单像素传感器制造总流程Fig.5 General flow of FSI single pixel sensor manufacturing

1）P 型衬底硅片的初始化，杂质浓度设置为1×1015cm-3。

2）制造浅沟槽隔离（STI）（图6），在硅片上生长一层薄氧化层，然后继续淀积一层Si3N4，通过有源区掩膜依次刻蚀Si3N4、SiO2、Si，形成沟槽；再次生长一层薄氧化层后淀积SiO2，剥离光刻胶，模拟CMP 技术对表面进行平坦化，然后刻蚀Si3N4与二氧化硅，最后生长一层牺牲氧化层用于在后续步骤中保护硅表面。

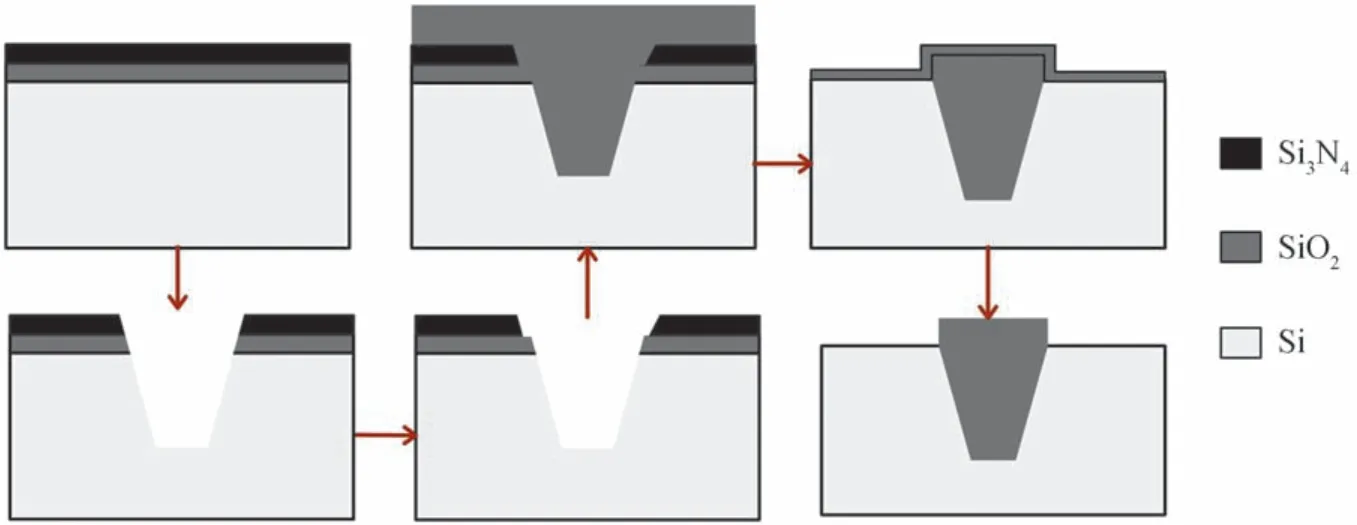
图6 STI 制造流程Fig.6 Flow of STI manufacturing

3）制造多晶硅栅，在栅氧形成后淀积一层多晶硅，然后构建栅极平面掩膜版图，按版图刻蚀多余的多晶硅以及栅氧。

4）光电二极管埋层N 型离子注入，沉积一层正向光刻胶，通过理论计算设计平面掩膜版的开口布局构建版图，按版图刻蚀光刻胶后注入磷离子，扩散时间可由特征长度的定义计算得到。设计光刻掩膜版时需要综合考虑器件整体结构布局与载流子运输方向，一般在二维平面上的线性梯度分布（图3），其光刻掩膜版对应的设计如图7（a），其浓度梯度会对载流子形成由原点由45°斜向上的运动趋势，如果将其直接应用在CMOS 像素中，因为光生电荷需要从收集区转移到FD 节点，在注入阶段需要将掩膜版顺时针旋转45°以保证载流子传输方向不会偏移。在这种情况下为了不影响其他环节的工艺，整个收集区需要缩小 2 倍，大大降低整个传感器的填充因子，为了避免这种情况，需要改变布局方案，本节像素设计时使用的掩膜版布局如图7（b）。在保留横向线性梯度的同时，舍弃了纵向的线性分布，取而代之的是制造两个浓度梯度差，保证载流子运输趋势不变。如果在更大尺寸的器件上应用时，为了满足精度的需要，可以适量增加纵向梯度的数量。

图7 光刻掩膜版布局设计示意Fig.7 Schematic of lithography mask layout design

5）轻掺杂源漏注入（Lightly Doped Drain，LDD），沉积一层光刻胶遮蔽住光电二极管区域，传输栅极由于还需要进行一次重掺杂，故可以不必完全遮蔽，节省光刻胶的使用。

6）制造Spacer，通过热氧化法以及二次生长，形成由上到下为二氧化硅-氮化硅-二氧化硅的结构，然后依次刻蚀三层，最后形成的spacer 宽度在0.08 μm 左右。

7）重掺杂源漏注入（Highly Doped Drain，HDD），使用光刻胶对包括光电二极管在内的像素感光区域进行遮蔽，然后进行源漏的N 型离子注入，同时也可以完成对多晶硅栅的重掺杂，减少额外的工艺步骤。

8）快速热退火，将整个像素环境快速加热至1 050 K，保持10 s 后，迅速完成淬火，消除由于注入掺杂离子形成的内部晶格缺陷。

9）制造电极，用于电学实验。利用目标电极位置构建电极版图，电极材料选择铝，位置分别在衬底底部，将从二极管传输来的电荷转化为电压信号的FD 节点（Floating Diffusion）以及传输沟道的多晶硅栅上。

10）沉积彩色滤光片和制造模拟微透镜。滤光片材料选择氮化物，遮蔽住除了光信号收集区即光电二极管的其他区域，在光电二极管上方添加球形微透镜，在透镜上方插入气体区域，模拟彩色滤光片，通过调整透射参数，可模拟不同波长入射的光学实验。

仿真完成后，用于电学实验和光学实验的像素结构如图8。

图8 像素三维结构示意Fig.8 Schematic of pixel three-dimensional structure

将设计的像素与传统工艺设计的像素切面进行对比，如图9（a）。

图9 梯度掺杂与均匀掺杂光电二极管横向掺杂分布对比Fig.9 Comparison of transverse doping distribution of gradient doped and uniform doped photodiodes

步骤4）中的扩散时间，由L=2Dt计算得到，D采用文献［25］的实验均值，而步骤5）到步骤8）等都涉及到了新的离子注入与额外的扩散时间，故像素PD 内的梯度掺杂区域最终的分布函数与预期值肯定会有一定的区别。图9（b）中非均匀掺杂曲线在前半段出现了非线性区域，这是由于在梯度掺杂的低浓度部分，离子注入阶段掩膜开口小，扩散阶段的扩散源相对也更少，对扩散时间的敏感度更高，而热退火等阶段相当于是对整个二极管区域进行了二次扩散处理，其电势分布如图10，可以看到在二极管内部形成了明显的电势梯度，且严格呈上升趋势。说明热退火等步骤对掺杂分布的影响不会形成势阱或势垒，因此，实际工艺中不需要为了获得严格的目标掺杂分布函数而修正本文理论的计算过程。这进一步证明了本文实现梯度掺杂的方法在实际生产时，可以直接应用理论计算的结果设置所需的工艺参数。

图10 梯度掺杂光电二极管区域的横向电势分布Fig.10 Transverse potential distribution in gradient doped photodiode region

4 像素性能分析

由于本文设计实验关注的重点在于通过制造像素PD 内部的浓度梯度，提升光生电荷的传输效率，为了让对照实验结果更具有说服力，对于表面暗电流、量子效率、填充因子等性能指标都不做特别的优化处理，尽量与传统工艺制造的像素保持一致。而目前在钳位光电二极管基础上发展出的降低表面暗电流的方法，改变像素阵列提升填充因子等方法以及用特定二极管结构提升量子效率等方法，与本文制造梯度掺杂的方法在实际工艺上并不冲突，在有相应需求的场景下，可以与这些技术良好的结合。

对传输门添加固定周期的梯形脉冲电压，高压时栅极打开，耗尽收集区的电荷，低压时栅极关闭。由于有入射光，收集区重新填充电荷，截取其中一个周期的栅极电压变化与读出信号对比，具有梯度掺杂分布的像素与传统均匀掺杂分布像素的对比如图11。

图11 栅极电压与读出信号对比Fig.11 Comparison between grid voltage and readout signal

同等条件下，具有梯度掺杂分布的像素一般情况下会具有更高的满阱容量。在设计对照实验时，如果光照、电压等实验条件完全一致，具有非均匀掺杂分布的像素在栅极电压的时序周期内不会完全耗尽，两个单像素传感器只会具有相近的动态范围。由图11可知，在同一周期，传统工艺制造的像素在信号的读出与复位阶段都会有明显的延迟，难以应用到高速成像等应用场景；具有非均匀掺杂分布的像素读出信号对栅极电压的响应基本达到了零延迟，在高速传输的场景下可以极大程度避免图像拖影等问题的出现。两个传感器像素分别在各自收集区可以完全耗尽的实验条件下，信号的读出对比如图12。

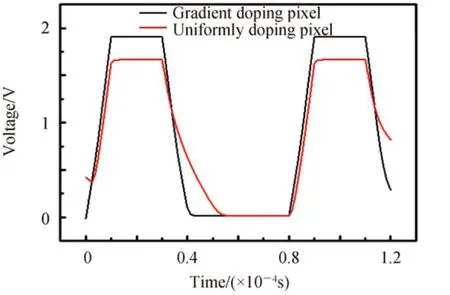
图12 收集区完全耗尽的读出信号对比Fig.12 Comparison of readout signals with completely depleted collection area

其中传统工艺制造的像素复位阶段响应时间为5.2×10-5s，而具有梯度掺杂分布的像素复位阶段响应时间为5.1×10-6s，复位阶段的响应速度提升了10 倍。除了具有更快的响应速度外，由于实验控制转换增益与暗态随机噪声相同，相较于传统工艺的像素，具有梯度掺杂分布的像素光响应的饱和电压为1.82 V，故其满阱容量与动态范围均提高了20%。

将本文提出方法设计的FSI 单像素传感器的4T 像素性能与参考文献进行对比，如表2所示。其中文献［22］像素为传统低压像素设计时采用的数字像素，工作电压低至0.5 V，但动态范围只有42 dB，随机噪声高达9.3%，响应时间为50 ms。文献［14］设计的大尺寸像素工作电压为1.8 V，动态范围只有51 dB，但随机噪声降低到了0.12%。文献［13］像素为前文对照实验中采用传统的均匀掺杂工艺设计的4T 像素。文献［12］采用的4T-PPD 有源像素在传统高压3.3 V 的工作模式下，动态范围高达69 dB，随机噪声为5.5%，应用本文方法设计的像素，在动态范围和读出噪声等指标上均可与之比拟，而设计过程相较其他方法更为灵活

表2 本文设计的FSI 图像传感器像素与参考文献对比Table 2 Comparison of FSI image sensor pixels designed in this paper and references

5 结论

本文提出了一种任意梯度掺杂分布的实现方法，证明了理论上只需要通过控制离子注入和扩散两个过程，就可以产生任意目标函数的掺杂分布。应用本文提出的理论在P 型硅衬底与传统前照式CMOS 单像素图像传感器上，设计并仿真了具有线性梯度浓度分布的光电二极管。实验结果表明，应用本文方法通过控制扩散时间与注入浓度，在单独设计光电二极管时，制造的梯度掺杂分布与目标分布基本一致。在应用到完整器件流程中时，由于除了制造非均匀掺杂区域的流程以外，需要多次掺杂与热退火等步骤，最终生成的梯度掺杂分布，在低浓度区与目标分布会有细微的偏移，但并不影响产生平滑的电势梯度。应用本文方法制造的像素在光生电荷的传输效率上较传统工艺提升显著，实现了接近0 延迟的信号读出。

本文提出的方法实施简单，仅针对目标区域的掺杂流程，不会影响后续工艺流程。为了保证方法的创新性与普适性，本文并未结合其他最新的优化方案进行验证，但理论上本文方法可以与特殊低串扰结构［26］等优化方案良好的结合。本文的理论分析具有较高的普适性，除了用于制造任意梯度掺杂分布外，也可以用于其他领域，如研究特定杂质在基底材料中的扩散系数，研究新型材料时确定其部分物理性质等。