单目显微成像系统三维形变测量方法

赵冉，李轩，刘波，焦朋，黄永刚，贾金升，4

（1 中国建筑材料科学研究总院有限公司 绿色建筑材料国家重点实验室，北京 100024）

（2 太阳能与建筑节能玻璃材料加工技术北京市重点实验室，北京 100024）

（3 中国建材检验认证集团股份有限公司，北京 100024）

（4 中建材光芯科技有限公司，山东 枣庄 277100）

0 引言

玻璃光纤、石英光纤等光学产品在工业生产中会因为承受多种理化作用而产生各种各样的形变［1］。虽然该形变仅为微纳米尺度，却足以对材料以及相关产品的性能产生严重的影响。以玻璃光纤耦合器件为例，当光纤的输出端面与耦合面之间的距离增加0.1 mm 时，光的传输效率会降低10%以上［2］。因此，在工业上每年需要投入大量时间与经费对材料的形变进行检测与监控，而显微观测则是检测的重要手段。

目前用于显微系统的三维形变测量方法主要有白光显微干涉法［3-4］、显微条纹投影法［5-6］、数字全息显微法［7-8］、三维数字图像相关法（3D Digital image correlation，3D-DIC）［9-10］等等。虽然白光显微干涉法的测试装置比较简单，但是该方法需要采集多幅图像才能完成测试，耗时较长无法实现快速工业检测；显微条纹投影法和数字全息显微法的测量装置通常较为复杂，对设备要求较高，同时以上方法均需要相位解包操作，这无疑增加了计算难度和测量误差；常规的数字图像相关法（Digital Image Correlation，DIC）是一种高精度、稳定性强的面内位移测量技术［11］，随着研究的不断深入，近年来研究人员提出了多种三维数字图像相关方法并在实时动态测量等领域得到了广泛应用。然而，三维数字图像相关技术通常需要两部工业相机或一部3CCD 相机（3CCD Camera）才能完成测试［10］，在工业生产中不可避免的振荡和扰动会增加此类双目或分束光路技术的检测误差。另一方面，由于单目显微成像系统（即一部普通工业相机与一部光学显微镜组成的单光路测量系统）是玻璃光纤元器件的工业生产中最常见的显微装置，从检测实用性和成本方面考虑，企业和生产线上的研究人员更期待基于单相机显微的三维形变测量方法。

图像球面化算法是赵冉等于2019年提出的一种机器视觉技术［12］，该课题组曾利用该算法成功解释了微通道板像旋转现象。由于能够模拟形变物体的反射图像，该算法为显微三维形变的测量提供了新的思路。本文提出了一种基于图像球面化算法的单目显微成像系统三维形变测量方法。首先由显微成像系统拍摄物体变形前后的两幅图像并计算图像之间的面内位移场，然后根据图像球面化模型从该面内位移场中提取离面位移，最终实现三维形变的测量。由于DIC 法［11］与光流（Optical Flow，OF）法［13］都是较为成熟的面内位移测量技术，为保障面内位移与离面位移的测量精度，在计算机模拟实验和应用实验中分别采用这两种方法提取面内位移。所有实验的离面位移测量结果的绝对误差均小于0.2 μm，证明了本文提出方法的有效性。该方法只需要一部工业相机拍摄显微镜下的两幅图像即可完成测量，充分利用了面内位移场携带的离面位移信息，提取离面位移时无需转换到频域和相位解包操作，适合于玻璃光纤、石英光纤等光学产品的工业检测。

1 测量原理

1.1 图像球面化算法与微分原理

图像球面化算法可以被定义为图像中某指定区域每个像素点沿该点与区域中心连线方向做扩张或收缩移动［12］。例如，当一幅图像被置于一块透明的球形玻璃下方时，经玻璃透射的图像可以被视为球面化图像，如图1。在图像球面化后，图1（a）中的A点会移动到图1（b）中的A'点。虽然直接看到的是A点在平面内的二维运动，但是它却包含了三维运动的信息。

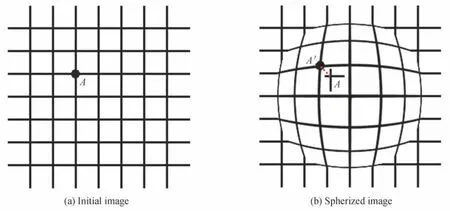
图1 图像的球面化Fig.1 Image spherizing

由微分理论可以得知，任何曲线都可以被看作无穷多微小线段的累积，如图2。从这一思路出发不难想到任何球形或者半球形的形变都可以被看作是无穷多微小斜面的积分。基于此，可以将光学显微镜下看到的任何形变均当作斜面形变。

图2 微分理论Fig.2 Differential theory

1.2 最简单的斜面模型

首先考虑最简单的斜面形变情况，如图3（a）所示，斜面的临边（Adjacent of slope）是斜面的斜边（Hypotenuse of slope）在x-y平面上的投影并且平行于x轴。为方便分析，图3（b）展示了将坐标轴平移后（O点坐标变为（0，0））该模型在x-z平面的截面图。将样品在x轴方向上抬起一个小角度θ，A点被抬起到A1点，A'为A1点在x轴上的投影，O为支点，R=OA=OA1为图像宽度。由图像球面化原理可知，在实际看到的二维形变图像中A点会移动到A'点的位置，其中面内位移为d=AA'，离面位移为w。在得到变形前后的两幅图像后，根据DIC 法或者光流算法均可以得到面内位移d，图像宽度R为已知量，由于

图3 最简单的斜面形变模型Fig.3 The simplest slope model

因此可以得到斜面倾角

最后根据式（3）得到离面位移

1.3 常规的斜面模型

在图3（a）中斜面的临边与x轴是平行的，即图3（b）中的A点、A'点与支点O都处于x轴上，但在实际测量时OA与x轴应当存在一定夹角。设斜面在x-y平面上旋转的角度为δ，O'在δ角度方向的延长线与图像交于O点，如图4所示，此时拍摄区域内的每一点对应的宽度R需要重新计算。首先需要说明的是，旋转角度可以由DIC 法或者光流法得到，其中u（xi，yi）和v（xi，yi）为图像中某点A'（xi，yi）在水平方向与竖直方向上的面内位移。将坐标轴平移，设O（0，0）为拍摄图像坐标轴的原点，在x-y平面内做OO'的垂线BC，若直线OO'的斜率k=tanδ，则直线OO'的公式为y=kx且直线BC的斜率为过A'点做BC的平行直线并与OO'的延长线交于O1点，则点A'在斜面模型中对应的图像宽度R应等于OO1的长度。由于直线A'O1的斜率为且过A'（xi，yi），直线A'O1的方程可以被表述为设点O1的坐标为（x0，y0），联立方程组

图4 常规斜面模型Fig.4 General slope model

最终根据式（2）与式（3）即可求得离面位移w。

综上所述，常规斜面模型的三维位移测量过程可以分为以下三步：

1）在获得变形前后的图像后，根据DIC 法或光流法测量得到两幅图像间每一点的面内位移u（xi，yi）和v（xi，yi）；

3）根据式（2）与式（3）求得每一点的离面位移w（xi，yi），完成三维位移测量。

2 模拟实验

在模拟实验与应用实验中选用光纤倒像器作为实验测试样品。由于光纤单丝产生的光强分布的数学模型可以被认为是高斯函数［2，14］，因此可以使用由Matlab 软件生成的二维高斯函数阵列来表示光纤倒像器在显微镜下拍摄的二维图像，如图5（a）、图5（b）所示。其中图5（b）是由图像球面化算法对图5（a）进行形变加载得到的，加载的斜面角θ=0.2 rad≈11.46°，加载的旋转角度δ=45°，即图3（a）中斜面的临边与图像的对角线平行，图像在形变后会沿对角线方向平移，对角线的两个端点（即图5（a）中的顶点Vertex 和底点Nadir）应为图中平移量最大与最小的位置。两幅模拟图像的宽度均为400 pixels ×400 pixels，以光强衰减至二维高斯函数强度的1/e 位置为芯皮分界线，芯皮直径比被设置为1∶5。图5（c）展示了图5（a）、图5（b）沿对角线方向的图像灰度分布。从图5（c）中可以看出，形变前后的图像灰度是沿对角线方向整体平移的，离面位移较大的位置面内位移也会增加，这与斜面模型是相符的。

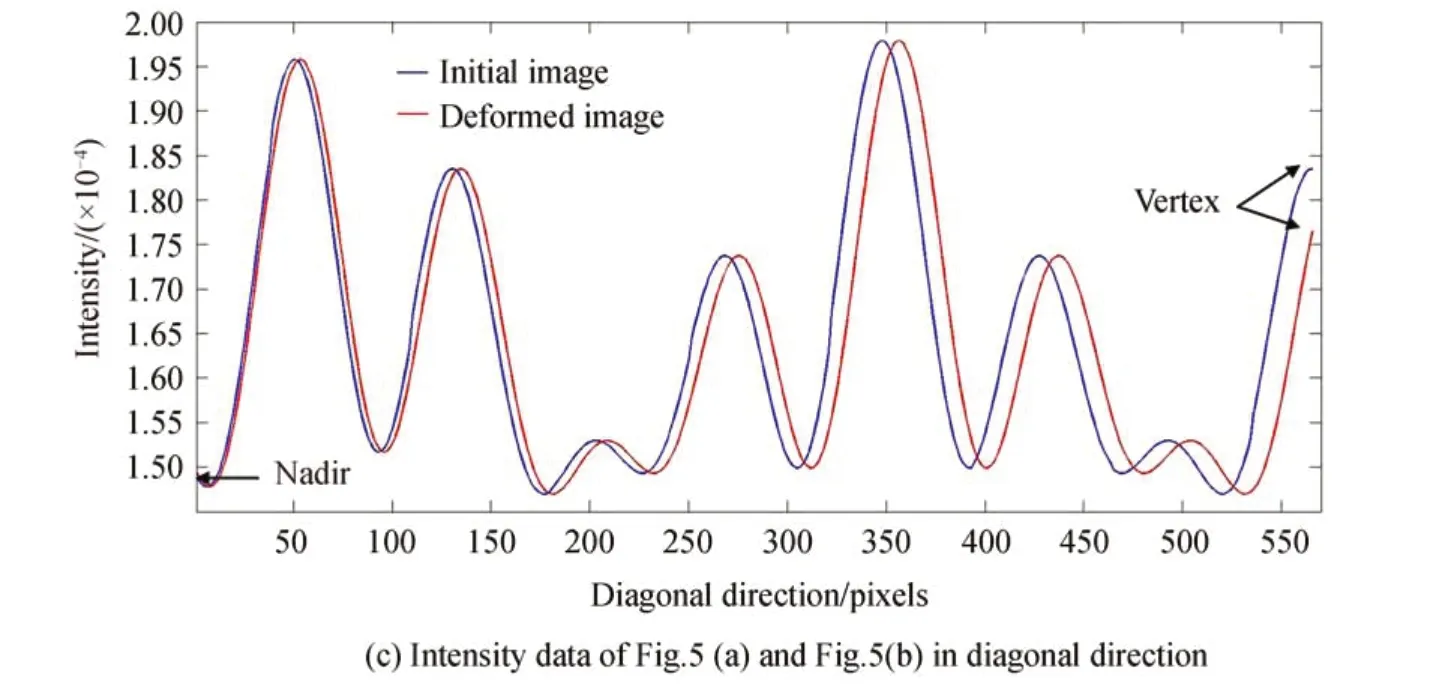
图5 模拟显微镜下光纤图Fig.5 Simulated optical-fiber image under microscope

采用基于梯度的DIC 法［11］和Brox 光流法［13］对变形前后的模拟图像提取面内位移，然后根据式（1）～（5）提取离面位移。由于DIC法和光流法本身的边缘效应，测量数据的有效区域为图像中央的340 pixels×340 pixels，共计115 600 个数据点，有效区域的对角线宽度为480.8 pixels。图6（a）～（d）展示了DIC 法和光流法测量得到的水平与竖直方向面内位移场u与v。由于旋转角度δ=45°，u场与v场的顶点与底点的理论值均为7.355 pixel，0.598 pixel，图6（a）～（d）中的测量值分别为7.375 pixels，0.586 pixel，7.461 pixel，0.588 pixel，7.335 pixels，0.599 pixel，7.336 pixels，0.598 pixel。对每一个数据点的面内位移计算x-y平面内旋转角度δ，均值为45.01°。

图6 模拟实验面内位移测量结果Fig.6 In-plane displacement results of simulation experiment

DIC 法与光流法的测量的离面位移结果以及理论值如图7（a）～（c）所示。为进一步验证测量精度，图7（d）展示了图7（a）～（c）在图像对角线方向上的数据对比，表1展示了图7（d）中顶点与底点数据。如果定义绝对误差（eA）和相对误差（eR）为

图7（d）中DIC 法与光流法所有数据的相对误差均值分别为2.1%和1.3%，绝对误差都小于1 pixel。从表1中也可以看出，两种方法算出的顶点和底点的绝对误差都小于1 pixel，对应的斜面倾角θ的相对误差仅为0.5%和0.7%，证明了离面位移与面内位移的测量精度（由于离面位移是根据面内位移的数据计算得到的，离面位移的测量结果足以证明面内位移测量的准确性）。另一方面，由于光流法引入了光滑因子［15］，在小位移测量方面具有更好的稳定性（通常小于3 pixels），而DIC 法在大位移（大于3 pixels）的测量方面更具有优势。从表1中也可以看出光流法在顶点和DIC 法在底点的测量误差略有增加，这与文献［15］中的分析是相符的。

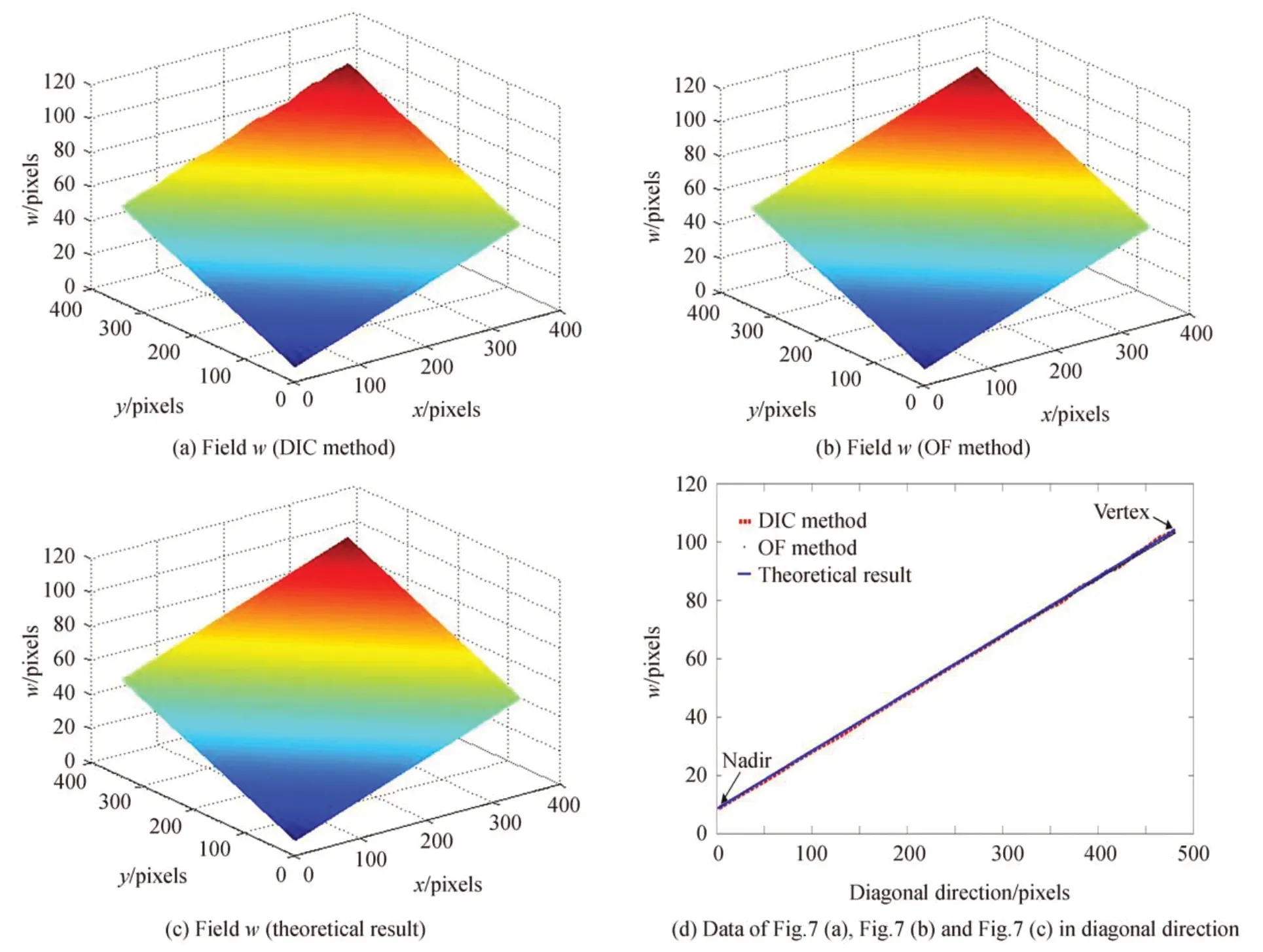
图7 模拟实验离面位移测量结果Fig.7 Out-of-plane displacement results of simulation experiment

表1 图7（d）中顶点与底点数据Table 1 Data of vertex and nadir in Fig.7（d）

3 应用实验

在应用实验中的测试样品为直径20 mm 的光纤倒像器成品，实验装置原理如图8（a）。光纤倒像器被固定在支架上，旋转支架上的手轮可以使材料倾斜。手轮上标有角度刻度，螺丝的螺距为200 μm，即手轮每旋转一圈倒像器的一端要上升或下降200 μm 的距离，因此可以根据光纤倒像器和支架的尺寸计算出倾斜的角度，如图8（b）。设螺丝的伸长量为s，选取的光纤倒像器直径S1=20 mm，螺丝与光纤倒像器之间的支架长度S2=5 mm，可以得到加载的倾角选用的光学放大显镜放大率为50 倍（NA=0.55，Mitutoyo，物镜：PLAN APO L，WD/20.5 mm），支架底座有可在z轴方向移动的平移台用于显微镜的对焦。选用的相机为Andor 公司生产的ZYLA 4.2 Plus（CMOS 芯片，芯片尺寸13.3 mm ×13.3 mm，像元尺寸6.5 μm×6.5 μm，靶面对角线宽度18.8 mm，最大分辨率4 632 pixels×3 488 pixels，全分辨率采集帧率可达100 帧/s，C 接口），实验装置如图8（c）、图8（d）。为了尽可能减少测量时的环境振荡引起的误差，所有的实验装置都被放置在气悬浮减震台上，减震台的振幅≤1 μm。

图8 实验装置与原理图Fig.8 Experimental setup and schematic diagram

实验前首先对光路进行严格校准以保障垂直拍摄。旋转手轮加载倾角θ=8°的斜面形变。为与模拟实验保持一致，通过载物台上的量角器调整x-y平面内的旋转角度δ，在拍摄完图像后利用Matlab 自带的Imrotate 程序对δ进行微调，最终使δ=45°（注：本文提出的模型在定标后对于任意旋转角度δ∈（0°，90°）均适用），拍摄的变形前后的图像尺寸也设定为400 pixels×400 pixels，1 pixel=80 nm，采用同态滤波法和维纳滤波算法对拍摄图像做预处理以最大限度保障图像质量，处理后的实验图像如图9（a）、图9（b）、图9（c）展示了图9（a）、图9（b）在对角线方向的灰度值分布情况。从图9（c）中可以看出，形变前后的图像灰度是沿对角线方向整体平移的，离面位移较大的位置面内位移也会增加，这与模拟实验的结果是一致的。

图9 光学显微镜拍摄的实验图Fig.9 Experimental images captured by microscope

DIC 法与光流法得到的面内位移结果如图10（a）～（d）。同样地，由于算法的边缘效应，测量数据的有效区域为图像中央的340 pixels×340 pixels，有效区域的对角线宽度为480.8 pixels=38.464 μm。图10（a）～（d）中顶点和底点的理论值为0.287 2 μm，0.023 3 μm，测量值分别为0.282 0 μm，0.049 1 μm，0.281 8 μm，0.044 5 μm，0.278 6 μm，0.029 4 μm，0.277 7 μm，0.028 8 μm。

图10 应用实验面内位移测量结果Fig.10 In-plane displacement results of application experiment

离面位移测量结果以及理论值如图11（a）～（c）所示，两种方法的测量时间分别为24.36 s 和19.55 s（运行环境为Matlab 软件，Intel i5-7400 CPU @3.0 GHz）。为方便进一步分析，图11（d）展示了图11（a）～（c）在图像对角线方向上的数据对比，表2展示了图11（d）中顶点与底点数据。图11（d）中DIC 法与光流法所有数据的相对误差均值为4.3%和2.9%。值得一提的是，从表2中可以看出，虽然DIC 法在底点的绝对误差小于0.1 μm，但是由于总的位移值较小，相对误差达到了11.35%，而光流法在底点的测量结果则明显优于DIC法；由于顶点的位移值较大，光流法在顶点的绝对误差超过了0.1 μm，但是DIC 法在顶点的绝对误差却在0.05 μm 以内。总体来看，DIC 法和光流法分别在测量小位移与大位移时准确度会降低，这也是导致所有数据的平均误差增加的最重要的原因。根据文献［15］的分析，本文提出了修正方案：采用DIC 法与光流法结合计算面内位移与离面位移值，面内位移水平与竖直分量小于或等于3 pixels（在50X 显微镜下约为0.25 μm）时测试结果主要以光流法为准，当面内位移水平与竖直分量大于3 pixels 时测试结果主要以DIC 法为准。但是也要注意到，由于1 pixel=80 nm，在应用实验中不管是DIC 法还是光流法测量的绝对误差均小于0.2 μm，两种方法都能够满足玻璃光纤、石英光纤等光学产品的工业测试需求［16］，证实了本文方法的有效性，因此该方法已用于该类光学产品工业生产的形变检测与监控过程之中。除此之外，当光纤传像材料的均匀度较差时，在同种理化作用下不同位置产生的形变量会有微纳米量级的差异。基于本文提出的测试方案，可以采用对比材料不同位置形变量的方式来评价产品均匀度的优劣，目前该方法也已被用于玻璃光纤、石英光纤等光学产品的均匀度评价与监控过程之中。

表2 图11（d）中顶点与底点数据Table 2 Data of vertex and nadir in Fig.11（d）

图11 应用实验离面位移测量结果Fig.11 Out-of-plane displacement results of application experiment

4 结论

基于图像球面化算法建立了常规斜面形变模型，并提出了一种单目显微成像系统三维形变测量方法。首先由单目显微系统中的工业相机拍摄物体变形前后的图像，采用DIC 法或光流法测量得到两幅图像间每一点的面内位移，最后根据常规斜面模型从面内位移中提取离面位移，完成三维形变的测量。模拟实验与应用实验的测量绝对误差均小于0.2 μm，证实了算法的有效性。该方法充分利用了面内位移场携带的离面位移信息，提取离面位移时无需转换到频域和相位解包操作，具有检测成本低、光路简单、普适性强、稳定性高等优势。该方法已被用于玻璃光纤、石英光纤等光学产品的工业生产检测与监控中，同时为固体材料的微纳米尺度形变动态测量提供了新的思路。