基于像差探测的太阳望远镜副镜姿态校正方法

王昆延，戴懿纯，金振宇

（1 中国科学院云南天文台 天文技术实验室，昆明 650216）

（2 中国科学院大学，北京 100049）

0 引言

地基太阳望远镜以高分辨观测为主要目标，对像质要求比较严格［1］。由于直接面对太阳进行观测，太阳望远镜在运行过程中更容易受到热等因素的影响，重力和温度作用会引起主副镜位置关系发生变化，导致时变像差，如果不改善，会影响高分辨观测的效果。口径越大，主镜焦比越小，望远镜像质对主副镜位置关系变化更为敏感［2］。为了更好地实现高分辨率成像观测，需要在运行过程中对望远镜的像质进行严格控制。副镜的口径较小，质量较轻，调节副镜可以减小功耗，工作效率更高而且调节起来较方便，采用具有六自由度调节能力的六杆机构调节副镜姿态来补偿主副镜位置关系变化导致的时变像差是目前常用的方法［3］。副镜相对于主镜的失调量的获取主要有两种方式。1）开环模式，根据望远镜的结构模型，指向高度和温度事先计算出副镜相对位置的改变量，望远镜运行时采用查表方式来实现姿态校正。如美国的8.4 m 大型综合巡天望远镜（Large Synoptic Survey Telescope，LSST）采用查找表在开环模式下实现副镜姿态校正［4］；2）闭环模式，根据实测的反馈信息实时调整副镜。反馈信息可以是失调量，如美国的大型双筒望远镜（Large Binocular Telescope，LBT）采用激光跟踪仪测量得到副镜的失调量［5］；也可采用波前探测系统作为副镜主动补偿的像差探测设备，为副镜主动调整提供实时的像差信息。如美国的1.6 m GST［6］和4 m Daniel K.Inouye 太阳望远镜（DKIST）［7］、德国的1.5 m GREGOR［8］均采用了S-H 波前探测系统探测望远镜像差，位于智利的维斯塔天文望远镜（Visible and Infrared Survey Telescope for Astronomy，VISTA）采用了曲率传感器进行波前测量［9］。

闭环校正模式中对失调量进行测量需要对测量方案进行精心的设计，该方法实际运用起来具有一定的难度。本文立足于采用波前探测的副镜姿态校正系统，研究如何利用测量像差更好的提取副镜失调量的方法，以及相应的实施方案。在基于像差探测的副镜姿态校正问题中，由于望远镜光轴的平移和倾斜存在耦合关系，它们都会导致系统的彗差，因此像差测量无法将二者完全区分，从而对副镜的姿态调整精度会产生一定的影响［10］。大视场的望远镜，可以在不同视场进行像差探测，通过不同视场的像差对偏心和倾斜进行解耦［11］，但是大口径的太阳望远镜往往采用格里高利光学系统，在主焦点附近设置热光阑，将大部分的光反射出主光路。受到主焦热光阑的限制，大口径太阳望远镜的视场通常只有3′～5′，由于视场较小，无法通过不同视场的象散进行解耦。对于大口径望远镜来说，为了减小耦合对失调量求解精度的影响，通常有两种方案。第一种方案是直接约束灵敏度较低的失调量，即不调整灵敏度低的失调量；第二种方案是采用正则因子来约束低灵敏度的失调量［7］。本文在采用正则因子约束低灵敏度的校正方案中，提出了两种失调量调整的实施方式。1）基于稳定0 点位置的失调量调整，即失调量每次的调整都相对于六杆机构初始的位置进行调整；2）相对位置的失调量调整，即失调量的调整相对于上一次调整后六杆机构的位置进行调整。本文以我国正在建设的2 m 环形太阳望远镜（2m Ring Solar Telescope，2mRST）的副镜姿态校正系统为例，结合六杆机构的执行精度，波前像差探测精度，首先研究了采用正则因子约束失调量的副镜校正方案；在此基础上，根据像差探测对失调量的探测灵敏度排序，探讨了直接约束两个低灵敏度失调量的校正方案；并对2mRST 副镜姿态校正系统提出了实施的技术要求。本文的研究不仅为即将建成的2mRST 副镜姿态校正提供了控制和实施方案，也可以为其他基于小视场波前像差测量的副镜姿态校正问题提供参考解决方案。

1 2mRST 及其副镜姿态校正系统

2mRST 主镜采用了创新的环形结构，外径为2 000 mm，环宽为350 mm，采用了图1所示的格里高利系统和地平式结构。光学系统的主要参数如表1所示。

图1 光学系统结构Fig.1 Optical system structure

表1 2mRST 主要光学参数Table 1 Main optical parameters of 2mRST

2mRST 副镜姿态校正的目标精度是使系统的strehl 比大于0.8，即波面均方根误差小于λ/14。2mRST的副镜姿态校正过程如图2所示，采用S-H 波前探测系统探测望远镜像差，将主镜作为参考，通过像差探测确定副镜相对于主镜的位置变化，利用六杆机构调节副镜以补偿主副镜位置失调对像质的影响。副镜相对于主镜的位置变化主要有六个自由度的变化，即沿着光轴的前后平移Dz（离焦），绕着光轴的旋转Tz，沿着垂直于光轴平面内的X轴和Y轴的平移Dx和Dy（偏心），以及绕X轴和Y轴的旋转Tx和Ty（倾斜）。由于副镜是旋转对称的，绕光轴的旋转不影响像质，因此副镜失调量主要包括Dx、Dy、Dz、Tx和Ty。经过前期的实测实验，S-H 波前探测系统的倾斜测量精度在平滑随机大气影响后，可以达到0.02″。六杆机构已经研制完成，由六根直线支链（直线位移促动器）与铰链组合构成。支链位移促动器采用简单易行的步进电机集成减速器的驱动方式，集成线性可变差动变压器作为支链伸缩量检测系统。经过测试其平移自由度的执行范围为±2 mm，分辨率优于0.1 μm；六杆机构旋转自由度的执行范围为±0.2∘，分辨率优于0.5″。

图2 副镜姿态校正过程Fig.2 The alignment process of secondary mirror

2 控制矩阵及其性能分析

副镜失调量的校正采用了灵敏度矩阵法［12-14］，建立副镜失调量与望远镜像差的对应关系。灵敏度矩阵法将表征系统波像差的Zernike 系数表示为不同失调量的线性组合，可以表示为

式中，Z为S-H 波前探测系统获得的Zernike 像差系数值；X为副镜失调量向量，A是灵敏度矩阵。副镜失调产生的像差主要是离焦像差和彗差，因此灵敏度矩阵的构建主要考虑Z4～Z9这6 个泽尼克系数。

根据2mRST 光学误差容限的分析，2mRST 在下述范围能获得较好像质，本文研究的失调范围为Dx=Dy=Dz=[ -0.1，0.1]mm、Tx=Ty=[ -0.007，0.007]∘。利用Matlab 和Zemax 混合编程技术在上述误差范围内随机生成1 000 组均匀分布的失调量，通过动态数据交换技术实现Matlab 对Zemax 中光学模型的参数控制和二者的数据传输。根据Zemax 获得的Zernike 像差系数，通过线性回归的方式，获得了失调量（Dx、Dy、Dz、Tx和Ty）和Zernike 系数（Z4～Z9）关系的灵敏度矩阵A。

对控制矩阵进行奇异值分解，即

式中，Σ=diag(σi)是对角矩阵，对角线上的值σi是Σ的奇异值（i是奇异值的编号），其按从大到小顺序排列；V与U是列正交酉矩阵。奇异值分解可以将多变量控制系统解耦为相互正交的控制模式（控制模式不同于控制变量即失调量，是失调量在正交模式下的投影），每个模式相对应的奇异值σi代表这种模式的探测增益［15］。由于副镜的偏心和倾斜存在耦合，2mRST 副镜姿态校正的灵敏度控制矩阵A有两个接近于0 的奇异值，即有两个无法探测的控制模式，控制矩阵的条件数较大（条件数为矩阵最大奇异值与最小奇异值的比值［16］）。以上的特点会导致两个后果：首先像差探测的微小扰动误差可能会引起失调量计算出现较大的偏差，而过大的失调量补偿要求可能会超出六杆机构的运行范围，对其造成损害；测量误差或者六杆机构的执行误差会在不可控模式上进行累积，导致最终失调量的计算无法收敛。

由于奇异值分解获得的奇异值排序不对应失调量本身的灵敏度排序，而是对失调量在U模式上投影的排序，为了获得失调量本身的灵敏度排序需要采用文献［7］中提到的模式截断算法。该算法由Golub 和Van loan 开发，在奇异值分解的基础上定义了截断矩阵为［7］

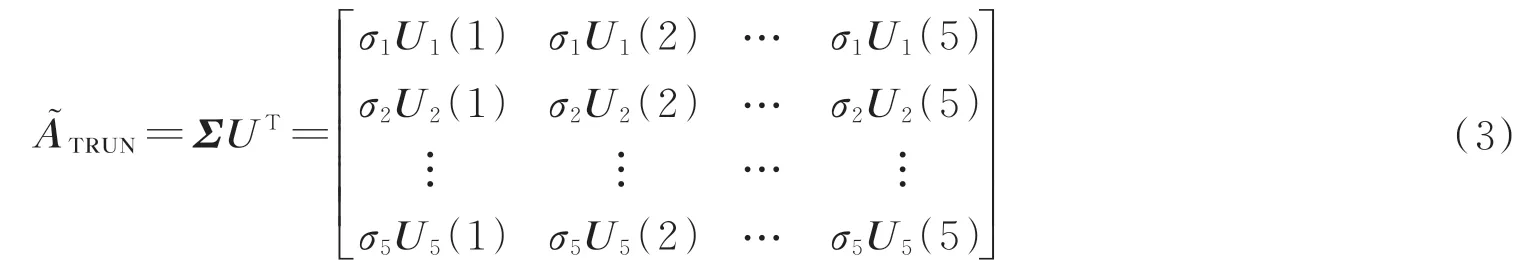
式中，U1～U5表示U的第1～5列。对进行奇异值分解

找到中最小的奇异值σi，然后找到的第i列）中绝对值最大值对应的下标j，其对应最不敏感的失调量，其灵敏度大小定义为σi/σ1。然后移除中的第j列形成新的截断矩阵

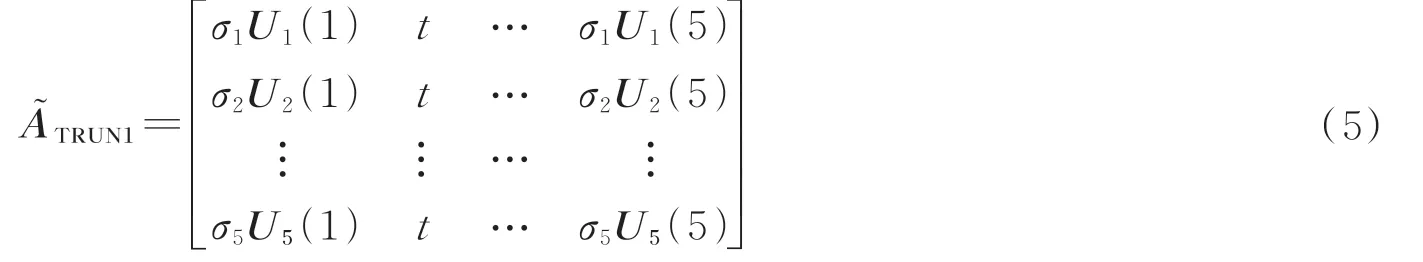
式中，t表示在原中被移除的列。对该算法进行迭代计算可以获得失调量的灵敏度排序。

利用该算法对副镜五个失调量的探测灵敏度进行计算并从低到高进行排序，结果如表2所示。

表2 失调量的探测灵敏度排序Table 2 Order of misalignment sensitivities

从表2可以看出，像差探测系统对副镜偏心的灵敏度低于副镜倾斜的灵敏度，副镜倾斜的灵敏度低于离焦的灵敏度。

3 失调量校正的约束方式和误差分析

3.1 正则因子约束低灵敏度失调量

由于偏心和倾斜存在耦合，控制系统中具有不可探测的模式，失调量的计算结果可能会出现较大偏差，执行量可能超出执行机构的运行范围。为了将失调量约束在一定范围内并提高失调量的求解精度，借鉴Tikhonov 正则化［17］的思路，在像差最小的优化方式上，以一定的权重增加对失调量本身的约束，其优化方式为

式中，C为正则矩阵，通常选取为单位矩阵I，a为正则因子。式（6）的解为

这种求解失调量的方法也被称作阻尼最小二乘法［18］，它的实施有两个关键环节。

1）正则因子a的合理选取。正则因子越大对控制误差的抑制效果越好，但是调整后的像差可能会较大，因此正则因子的取值需要在失调量最小与像差最小之间寻找一个平衡，使二者的值都能保持较小。

2）失调量调整的实施方式。在副镜姿态校正系统中，副镜失调量的调节是通过六杆机构各个支链杆长的变化进行的，采用逆运动学原理［19］可以获得失调量与六杆机构的杆长之间的映射关系，并且映射关系具有唯一性。六杆机构具有动平台和定平台，其中动平台与副镜相连。在六杆机构的空间坐标下，定平台具有稳定“0 点”，那么动平台在进行调节之前，在整个空间坐标系下也有稳定“0 点”位置，从而可以采用该“0点”位置来标定副镜失调量调节的起始点，失调量的每次调整都相对于这个“0 点”位置进行。这种方式称为“基于稳定0 点位置的失调量调整”，即式（6）中的X是相对于六杆机构初始的位置进行调整。与之相对的，是失调量的每次调整都相对于上次调整到的位置进行，不以六杆机构的“0 点”位置作为调整基点，这种方式称为“相对位置的失调量调整”，即式（6）中的X是相对于上一次调整后六杆机构的位置进行调整。接下来，我们采用相同的正则因子，对失调量调整的两种实施方案进行了仿真分析。

3.1.1 单次调整

进行单次调整时，并以六杆机构的“0 点”位置作为起始点，这时相对位置的失调量调整的基点也是六杆机构的0 点位置，因此相对位置的失调量调整与基于稳定0 点位置的失调量调整具有相同的效果。利用1 000 组探测像差数据反演副镜失调量，在1 000 组波前倾斜探测量上加入了探测误差，噪声量级参考了波前倾斜测量可能达到的精度，为0.02″。并且考虑了六杆机构平移自由度的执行误差为0.1μm，旋转自由度的执行误差为0.5″。

采用阻尼最小二乘法计算失调量时，正则因子的选取采用了L 曲线法，即获得像差和失调量随着正则因子变化的曲线，通过曲线的拐点确定正则因子［20］。在本文的模拟中，正则因子是通过分别求取1 000 组数据的正则因子，取其RMS 值获得，结果为0.111 1。实际控制的正则因子可以此为依据，根据控制效果进行选取。阻尼最小二乘法（Damped Least Square Method，DLSM）和最小二乘法（Least Square Method，LSM）求解失调量的仿真结果如图3～4 和表3所示。图3～4 中橙色直线的表达式为y=x，蓝色点的横、纵坐标分别为失调量的设定值和计算值，则y=x直线上的点表示失调量的计算值与设定值相等的理想情况。蓝色离散点离y=x这条直线越远，说明失调量的计算值和设定值偏离较远，即失调量求解精度低。表3为失调量解算的均方根误差（Root Mean Square Error，RMSE），是失调量求解精度的定量表示。

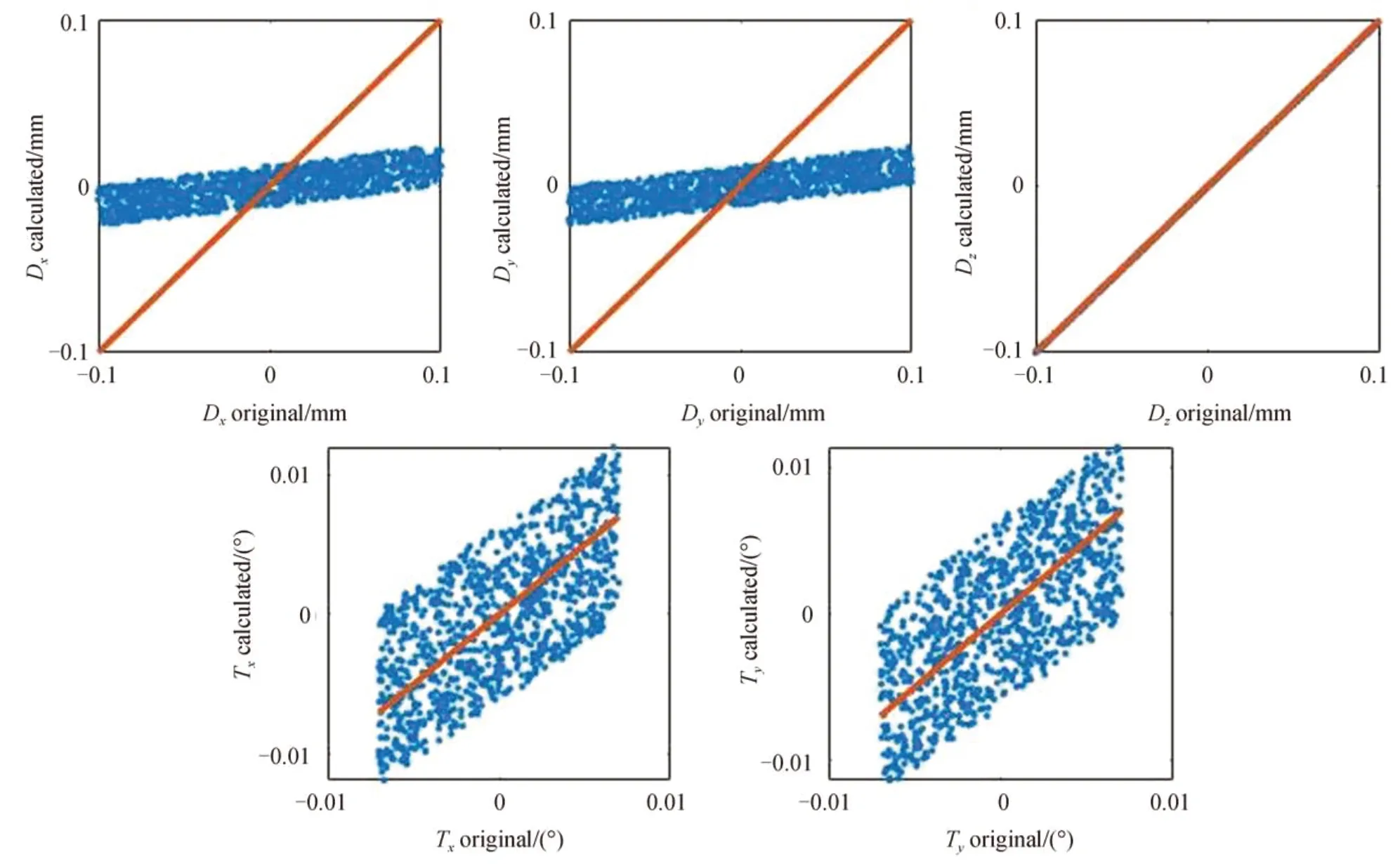
图3 失调量计算值与设定值比较（阻尼最小二乘法）Fig.3 Comparison between the calculated value and the original value of misalignment（damped least square method）

采用阻尼最小二乘法求解失调量，失调量校正前1 000 组像差的均方根值（Root Mean Square，RMS）值为0.495 9λ，校正后为0.006 2λ；采用最小二乘法求解失调，失调量校正前1 000 组像差的RMS 值为0.495 9λ，校正后为0.006 4λ。采用最小二乘法求解失调量，失调量校正后虽然像质得到明显改善，但从图3～4 和表3可以看出，相较于阻尼最小二乘法，最小二乘法的失调量求解精度较低，且求解的失调量弥散程度更大，有可能会超过六杆机构的调节范围。由于偏心和倾斜存在耦合，且单视场探测无法实现解耦，所以偏心和倾斜的求解精度不如离焦。在实际运用中应该加入正则项降低探测噪声对失调量计算的影响，将失调量约束在合理范围内，避免对促动器造成损害。

图4 失调量计算值与设定值比较（最小二乘法）Fig.4 Comparison between the calculated value and the original value of misalignment（least square method）

表3 失调量求解的均方根误差Table 3 RMSE of misalignment solution

3.1.2 连续调整

2mRST 一天的观测时间约为9 h。为了尽可能减小热对望远镜像质的影响，2mRST 主副镜之间采用了殷钢连接，根据殷钢的热膨胀系数与可能的温升，为了有效校正热致离焦，需要在1～2 min 完成一次副镜的姿态校正。因此在2mRST 一天的观测过程中，副镜持续的校正次数约为400 次。

图5为采用基于稳定0 点位置的失调量调整方案，考虑波前倾斜探测噪声（0.02″）和六杆机构执行误差（平移自由度：0.1 μm，旋转自由度：0.5″）时经过1 天的校正后各个失调量的累积误差。图6为采用相对位置的失调量调整方案，在相同探测噪声和执行误差下1 天的校正后各个失调量的累积误差。

由图5的仿真结果可知，采用基于稳定0 点位置的失调量调整方案，在有一定探测噪声和执行误差的实际系统中，失调量的调整始终在0 点位置附近，在持续一天的多次校正过程中不会产生明显的累积误差；而采用相对位置的失调量调整方案，如图6所示，在相同的探测噪声和执行误差下，多次调节后失调量会存在明显的累积误差。由于偏心和倾斜存在耦合，它们的求解精度低于离焦，相较于离焦，偏心和倾斜的累积误差范围较大。统计了10 组数据的累积误差，Dx、Dy、Dz、Tx和Ty累积误差范围的RMS 值分别为1.78 mm、1.33 mm、0.14 mm、0.09°和0.13°。2mRST 采用的六杆机构平移自由度的行程范围为±2 mm，仿真结果显示偏心量的调整可能会超出六杆机构的行程范围，会对其造成损害。

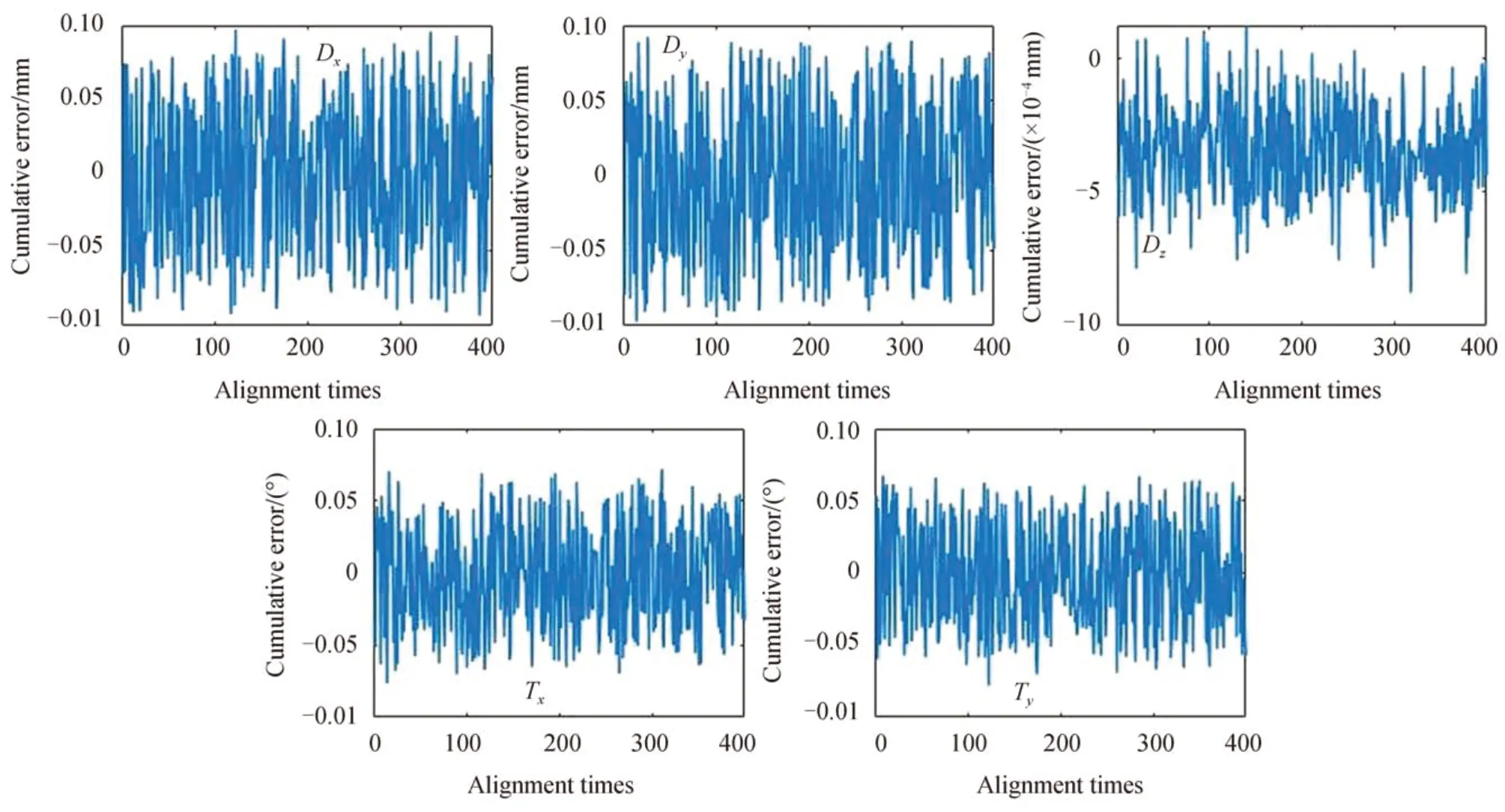
图5 1 天校正后失调量的累积误差（基于稳定0 点位置的失调量调整）Fig.5 Cumulative error of misalignment after 1 day alignment（alignment based on stable 0-point position）

图6 1 天校正后失调量的累积误差（相对位置的失调量调整）Fig.6 Cumulative error of misalignment after 1 day alignment（alignment based on relative position）

3.2 直接约束低灵敏度失调量

本文还尝试直接约束低灵敏度的失调量，即不调整偏心，用副镜倾斜补偿偏心的影响，并评估其补偿效果。偏心被约束时，通过线性回归方式，获得了失调量（Dz、Tx和Ty）和Zernike 系数（Z4～Z9）关系的灵敏度矩阵A1。矩阵A1的条件数为5.945 5，由于控制矩阵是良态的，此时可以通过最小二乘的方法求解失调量。波前倾斜探测噪声为0.02″，并且考虑了六杆机构的执行误差（平移自由度：0.1 μm，旋转自由度：0.5″），然后通过最小二乘法求解Dz、Tx和Ty，仿真结果如图7和表4所示，失调量校正前1 000 组像差的RMS 值为0.495 9λ，校正后为0.127 4λ。直接约束偏心和采用正则因子约束低灵敏度的失调量两种方案对像质的补偿效果如表5所示。

图7 约束偏心时失调量计算值与设定值比较Fig.7 Comparison between the calculated value and the original value of misalignment for restricting decenter

表4 约束偏心时失调量求解的均方根误差*Table 4 RMSE of misalignment solution for restricting decenter*

表5 像质补偿效果Table 5 Image quality compensation effect

上述的解算结果表明，直接约束偏心量，调节离焦和倾斜量能够对像质有一定的补偿，但其补偿效果达不到2mRST 的目标精度，且倾斜量的求取精度和校正后的像质均不如采用正则因子约束低灵敏度的失调量时。采用正则因子约束失调量方案时，失调量校正后能将像质改善到波面均方根误差小于λ/14。

图8给出了调节量为Dz、Tx和Ty，而Dx和Dy不调节，当倾斜量测量噪声为0.02″，且考虑了六杆机构执行误差时经过1 天的失调量校正后各个失调量的累积误差。统计了10 组数据的累积误差，Dx、Dy、Dz、Tx和Ty累积误差范围的RMS 值分别为1.95 mm、1.45 mm、4.74 mm、15.17°和10.31°。这时由于偏心不调节，偏心上的累积误差会引起倾斜量的调节范围变大，对离焦量的调节也会造成一定的影响，在实际的副镜姿态调节过程中，这种累积误差的影响会更大。

图8 约束偏心时1 天校正后失调量的累积误差Fig.8 Cumulative error of misalignment after 1 day alignment for restricting decenter

4 结论

本文以2mRST 为例，探讨了基于小视场的波前像差探测如何进行副镜失调量解算和副镜姿态校正的方法，为即将建成的2mRST 副镜姿态校正提供了控制和实施方案。针对波前探测无法实现副镜偏心和倾斜解耦的问题，首先研究了采用正则因子对失调量进行整体约束的校正方案，并提出和分析了正则因子对失调量约束的两种实施方案。采用基于稳定0 点位置的失调量调整方案，能够有效的降低探测噪声和执行机构误差对校正效果的影响；采用相对位置的失调量调整方案，随着调整次数的增多，存在误差累积的问题，且偏心和倾斜存在耦合导致偏心和倾斜的求解精度低，累积误差范围更大。并且随着探测和执行环节的精度降低以及校正频率的升高，误差累积的速度会增大，失调量的执行会超过六杆机构的行程范围，可能会对机构造成损伤。采用相对位置的失调量调整方案，对执行机构的执行误差和探测噪声具有更严格的要求，为了保证校正的有效性，需要根据实际的系统噪声量级和校正频率以一定的周期对六杆机构进行复位。本文还根据失调量的灵敏度排序，探讨了直接约束灵敏度较低的偏心进行副镜姿态校正的可行性。这种方案对像质虽然也具有一定的补偿能力，但校正后波面均方根误差大于λ/14，达不到2mRST 的目标精度要求。失调量求解精度也不如采用正则因子对失调量进行整体约束的方案，并且由于偏心量不参与控制，偏心量上的累积误差还会加剧失调量偏离六杆机构调节范围的程度。对于基于小视场像差测量的副镜姿态校正系统，通过六杆机构杆长的起始位置对失调量进行“0 点”标定，在像差最小的基础上，并且以一定的正则因子对失调量进行整体约束是更适合的校正方法。该方法能够将波面均方根误差从0.495 9λ改善到0.006 2λ，达到了2mRST 的目标精度要求。2mRST 预计年底能够建成，待望远镜建成后，将在2mRST 上验证方案的有效性。