焊管冷弯回弹曲线方程构建及工艺优化
赵月伟,帅美荣,楚志兵,桂海莲,赵晓东,高虹,邬莉华,翟丽丽
塑性成形
焊管冷弯回弹曲线方程构建及工艺优化
赵月伟1,帅美荣1,楚志兵1,桂海莲1,赵晓东1,高虹2,邬莉华3,翟丽丽2
(1.太原科技大学 重型机械教育部工程研究中心,太原 030024;2.武进不锈股份有限公司,江苏 常州 213111;3.中钢不锈钢管业科技山西有限公司,太原 030600)
研究316L奥氏体不锈钢板材JCOE弯曲卸载回弹和应力分布特征,对预弯曲量实施相应补偿,以提高弯曲成形精度。基于弹塑性变形理论,利用有限元模拟研究各关键成形参数对板材弯曲卸载回弹的影响规律,将影响指标线性/非线性拟合叠加,构建回弹曲线方程。板料回弹量与上模下压量、下模开口量呈线性关系,与上模下行速度、摩擦因数呈指数关系。优化后的最佳冷弯成形工艺参数如下:上模下压量为12 mm,下模开口量为150 mm,上模下行速度为4 mm/s,摩擦因数为0.15。对于径壁比值≤10的板料成形,理论计算得到的弯曲回弹量与实测平均值吻合较好,构建的模型可以为实际生产奠定理论基础。
焊管冷弯;回弹解析;回弹方程构建;工艺优化
海洋油气资源开发工程装备是海洋经济的先导性产业之一,其蓬勃发展将直接推动各类配套管材制造业的快速发展[1-2]。美国、日本和欧洲油气输送管材生产商普遍采用直缝埋弧焊管,其主要生产工艺是UOE和JCOE工艺[3-5]。无论采用哪一种制管工艺,成形路径都比较长,多次弯曲回弹历史的累积效应与板坯初始形状、材料性能参数、模具结构参数以及工艺参数等影响因素有关。因此,确定多种因素及其耦合作用对管坯成形与回弹的影响、提高产品精度是工业生产中迫切需要解决的问题。
Gattmah等[6]研究了钢板在不同几何参数下的变形行为,采用双面渐进成形方法,提高了弯曲过程的几何误差。Pourboghrat等[7]根据板料曲率与横截面弯矩关系,分别利用各向同性强化和线性随动强化2种方式对板料弯曲回弹量进行计算,结果表明,在有明显包辛格效应的情况下,线性随动强化材料模型对回弹预测效果更好。Padghan等[8]根据板料材料特性和几何参数计算弯曲力,研究了一种人工神经网络和有限元方法,估算了钢板弯曲过程中的回弹值。刘克进[9]对凸弧翻边、凹弧翻边、V形弯曲和U形弯曲等典型冲压工艺进行了回弹试验研究,同时结合遗传算法,获得了具体材料和工艺条件下的回弹经验公式。
近年来国内外学者围绕耐腐蚀焊管成形技术进行了大量研究,该工艺技术在市场上得到了广泛应用。但国产同类不锈钢管材质量与国外先进水平相比还有一定差距,特别是部分大中口径、厚壁管材成形后的尺寸误差、表面缺陷等问题比较突出,在一定程度上影响了产品质量。文中针对316L奥氏体不锈钢直缝焊管JCOE生产技术,采用ANSYS有限元数值模拟技术,通过构建模型以及对弯曲成形质量进行深入分析,构建冷弯回弹曲线方程,对预弯曲量实施相应补偿,实现JCOE管材精确成形,从而为该类型焊管成形技术奠定理论基础。
1 弯曲回弹解析
板料弯曲是一种典型的弹塑性变形过程,当外力载荷卸除后,板料的体积和形状必然产生部分回复,具体表现为弯曲角度和曲率半径的变化。在弯曲初始阶段,弯曲半径比较大,内外部边缘应力强度要远远低于屈服极限,在变形时表现出较强的全弹性弯曲[10-11];随着弯曲半径的减小,变形区内外边缘先进入塑性变形状态,并向板料原始中性层位置扩展,此时板料处于弹塑性变形阶段,且靠近中性层区域属于纯弹性应变状态,应力随厚度呈线性分布,这一区域外为弹塑性变形区,其应力大于屈服应力,应力–应变不再是线性关系[12-13]。下面为简化弯曲回弹过程,进行如下假设[14]:(1)板料变形区的应力–应变状态为“三向应力,平面应变”,在板料宽度方向上应变为0,在厚度方向上应变呈线性分布,遵循=/,其中为质点与中性层的距离,为中性层半径,为应变;(2)靠近中性层区域,应力沿厚度方向呈线性分布,在此区域外呈非线性关系;(3)在弯曲过程中板料纵向纤维无挤压,不存在纤维之间的横向应力;(4)板料的弯曲变形被认为是理想弹塑性变形。
弯曲切向应力在弯板横截面上合力必为0,即凸侧拉应力与凹侧压应力之和为0,只需计算1/2截面上的应力再乘2即可,弯曲回弹反弯矩的计算见式(1)。
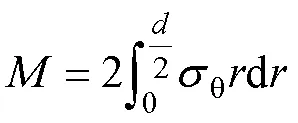
式中:为板料厚度;θ为切向应力。
可分解为弹性与弹塑性变形对应的瞬时回弹与滞后回弹所产生的弯矩,如式(2)所示。

式中:为弹性模量;为回弹前弯曲半径;s为屈服应力。对式(2)积分可得:

在弯曲后卸载过程中,可以认为在塑性变形反方向上增加一个理想的弹性弯矩−[15],产生的等效弹性变形满足式(4)。

进而求得等效弹性应变为:
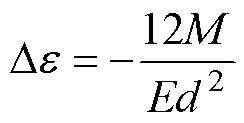

式中:为回弹后弯曲半径。
式(6)两端同乘并整理后,得到关于回弹前弯曲半径的一元三次方程,如式(7)所示。



根据回弹后弯曲半径的屈服强度s以及板厚,可以直接计算获得变形尺寸所需的弯曲半径。
板料弯曲挠度分为直边段与圆弧段2部分,且随弯曲半径的变化而变化,由几何关系建立弯曲半径与挠度的关系式见式(11),回弹量表征如图1所示。


式中:为板料弧长;为板料直边长;Δ0为回弹量;1为回弹后挠度;2为回弹前挠度。

图1 回弹量表征
2 有限元模型
304L、316L、S32205、S31803等奥氏体不锈钢具有耐低温、抗氧化、耐腐蚀等特点,适用于海洋的复杂环境,而且具有超低温韧性,在–100 ℃甚至更低的工作温度下,能有效防止恶性脆性断裂[16-18],文中研究材质为316L不锈钢,尺寸规格为20 mm× 400 mm×80 mm。
JCOE冷弯上模曲率半径为250 mm,下模圆角半径为30 mm,为保证变形精度,网格划分选用六面体主导且中间密两端疏的形式,板料中心150 mm段局部加密,该段网格划分沿宽度方向、长度方向、厚度方向分别为120、32、8层,板料整体划分共16 618个单元,上下模均为刚体。材料模型为双线性强化模型,可以同时反映材料的弹性属性和硬化效应,使材料变形前后应力分布更接近真实情况。设定弹性模量为196 GPa,塑性模量为1.87 GPa,初始屈服强度为238 MPa,抗拉强度为552 MPa,泊松比为0.3。假设在整个弯曲过程中板料与周围介质无热交换,接触类型为有摩擦接触,接触法向刚度为0.1,构建的有限元模型如图2所示。随着上模持续下移,板料开始发生弹塑性变形,通过改变单一变量,提取有效节点应力、回弹量等数值,分析关键工艺参数对成形过程中应力–应变以及卸载回弹的耦合影响。
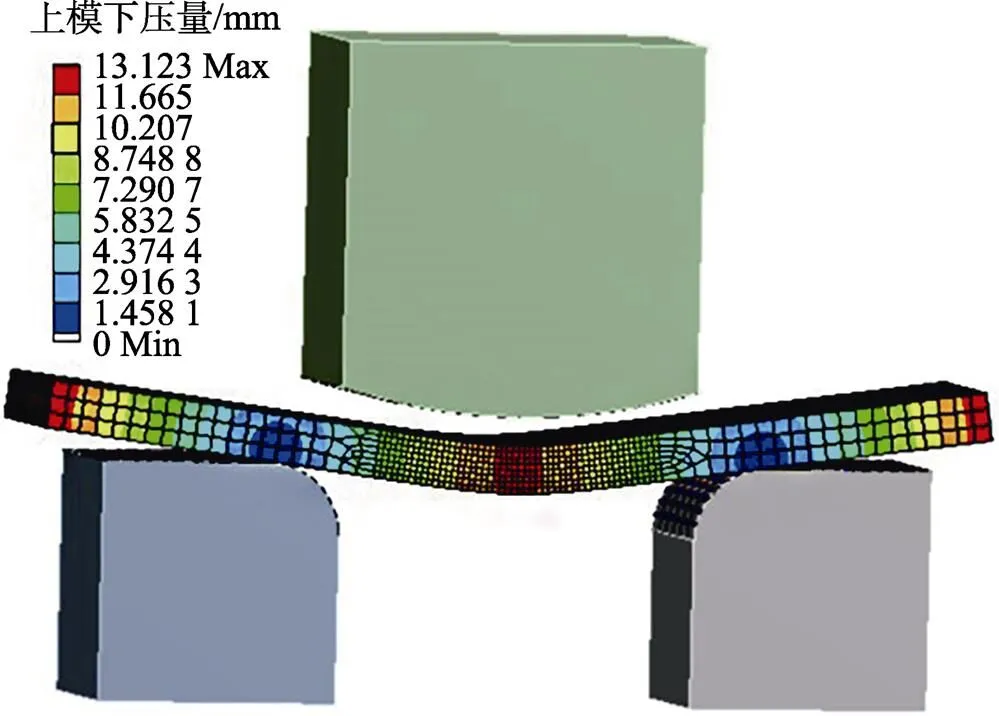
图2 有限元模型的建立
3 工艺参数对板料回弹的影响
3.1 上模下压量
在JCOE冷弯模拟中,上模下压量以凸模刚接触板料处为起点,凸模依次向下压8、12、16 mm。此时下模开口量为150 mm,上模下行速度为4 mm/s,摩擦因数为0.15。如图3a所示,随着下压量的增加,外层金属承受的拉应力与内层金属承受的压应力均增大。当上模下压量增大到16 mm时,如图3b所示,最大应力沿接触宽度向外大幅扩展,这主要是因为随着上模下压量的增加,板料弯曲角度过大,但由于受到下模开口量的限制,凸模中间区域与板料产生间隙,凸模两侧与板料发生部分接触,如图3c中板料中心位置与凸模之间的白色区域,此时板料变形区已不是此前的包覆状态,弯曲塑性变形区增大。随着下压量的增加,加载时弯曲区最大周向应力向两侧扩展,致使所需成形弯曲力急剧增加,材料发生弹塑性变形,如图3d所示。
以板料中性层中点作为中心,取长度100 mm作为弯曲回弹测试范围,用挠度D来表示弯曲回弹量。如图4a所示,沿着变形区,板料回弹分布大致呈二次函数曲线,回弹由弯曲中心向两侧减小。从图4b可以看出,当上模下压量为8~14 mm时,上模下压量与板料弯曲最大回弹量呈线性关系,此时上模下压量每增加2 mm,板料卸载回弹变化幅度不大,这对回弹控制十分有利,可以通过适当增加下压量对弯曲进行补偿,提高管材尺寸精度。然而,当下压量增大到16 mm时,回弹量显著增大,将不再遵循线性回弹规律。

图3 不同下压量变形区应力分布

图4 变形区回弹变化
3.2 上模下行速度
由于受到三点弯曲工艺及调速限制,模拟上模下行速度为2、4、6、8 mm/s,此时下模开口量为150 mm,上模下压量为12 mm,摩擦因数为0.15。从图5a可以看出,弯曲回弹量由弯曲中心向两端迅速减小,且随着下行速度的增大,板材回弹量有效降低。
考虑到模拟过程中上模下行速度变化范围较小,材料屈服强度变化不大,因此可以认为随着下行速度的增大,材料弹性变形能增大,弯曲回弹增大。在高速弯曲过程中,板材会产生变形热和摩擦热,促使金属软化,而且当这种高速变形软化效应大于硬化效应时,卸载回弹减小[19-21]。如图5b所示,当上模下行速度高于6 mm/s时,最大回弹量显著降低,这正是由软化效应导致的。此外,提高变形速度也会增加惯性效应,在一定程度上减小回弹量。
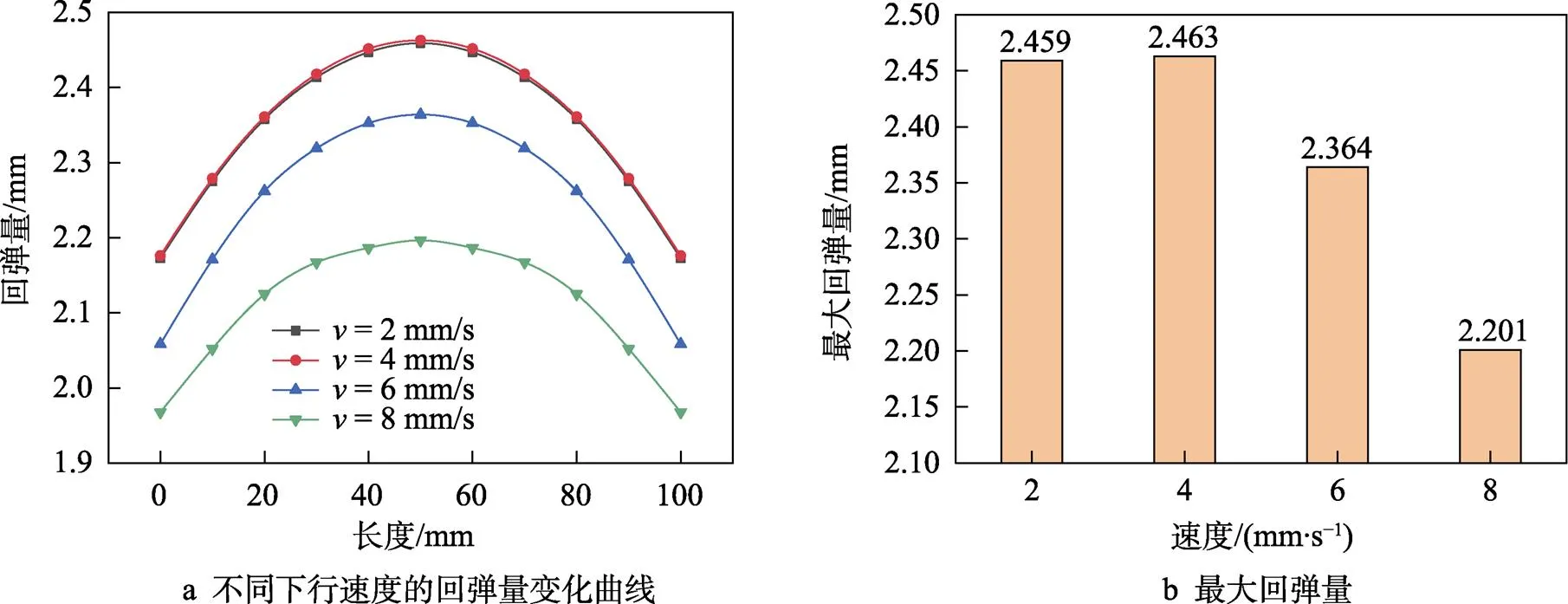
图5 弯曲速度与回弹的关系
3.3 下模开口量
选取下模开口量为150~200 mm,以为10 mm为间隔,保证上模下压量为12 mm、上模下行速度为4 mm/s、摩擦因数为0.15不变,进行有限元模拟。通过有限元模拟板料弯曲中间段回弹量如图6a所示,可以看出,下模开口量在150~180 mm时板料回弹量变化较小,变化幅度约在0.05~0.17 mm之间。图6b为不同开口量下弯曲中心区的最大回弹量,可以明显看出,当开口量增至200 mm时,最大回弹量接近4 mm,卸载回弹最为显著。
当上模下压量一定,下模开口量越大,板料弯曲区变形程度越小,材料弹性变形所占比例越大,卸载后弯曲回弹量越大。过大的开口量会引起弯曲曲率半径变化增大,与理想曲率偏差更大。相反,如果弯曲变形区减少,两边的直边段会加长,如图1所示,多道次成形影响管材圆度,为后续焊接和扩径工艺造成质量隐患。为更好地控制冷弯回弹量,应使开口量控制在150~180 mm之间。
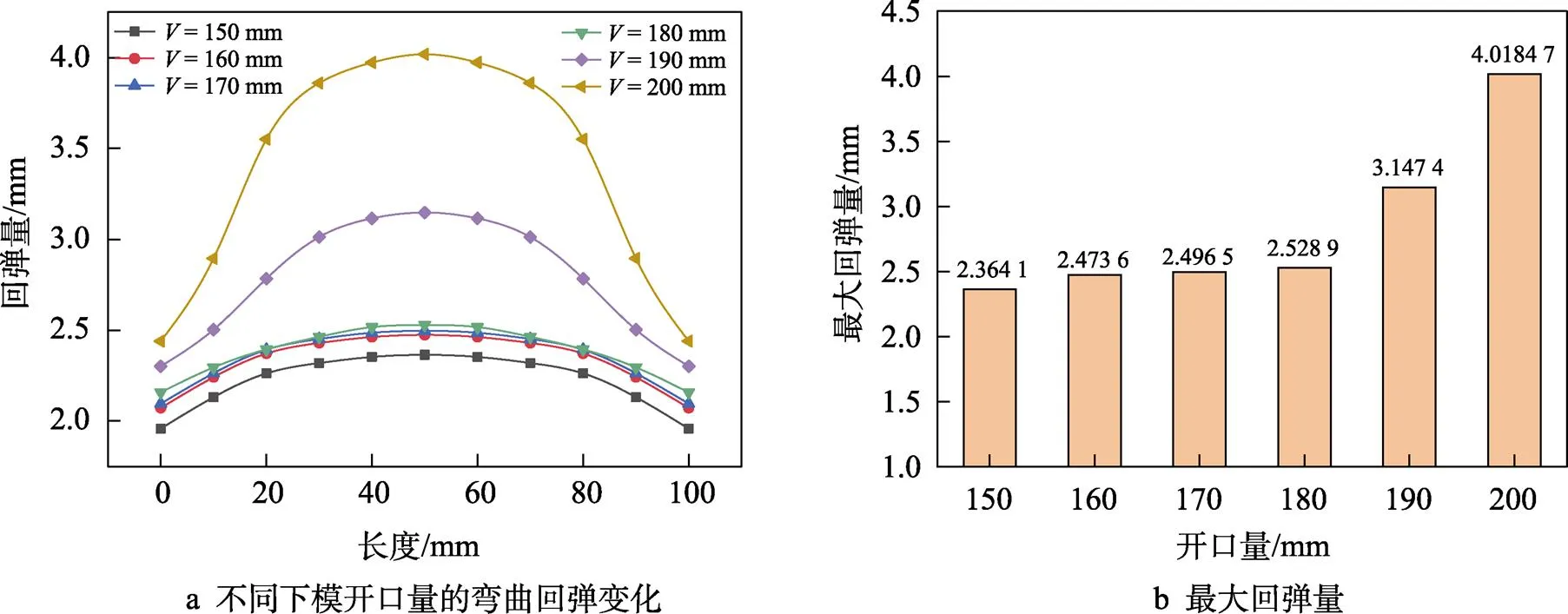
图6 下模开口量与回弹的关系
3.4 摩擦因数
在板料弯曲变形过程中,发生的主要摩擦是下表面与下模圆角的相对滑移和上表面与上模之间的摩擦,模具及板料的粗糙程度对弯曲成形性及板材外表面质量有一定的影响。摩擦因数为0.05、0.15、0.25时的板料回弹量如图7所示。可以看出,当摩擦因数为0.25时,回弹影响显著,板料回弹量最大值为3.06 mm。这是由于在板料弯曲过程中,上模对板料的摩擦力沿切向方向向外,而内表面积不断减小,板料表层的摩擦力将阻碍弯曲变形,卸载后回弹显著。
综合考虑,板料最佳冷弯成形工艺参数如下:上模下压量为12 mm,下模开口量为150 mm,上模下行速度为4 mm/s,摩擦因数为0.15。

图7 不同摩擦因数的弯曲回弹变化
4 回弹模型建立及验证
4.1 回弹方程构建
在成形过程中,板料不仅受到材料力学性能的影响,还受到上述诸多几何参数对回弹成形质量的耦合影响,因此需要对式(10)进行优化以提高计算精度。采用解析表达式逼近离散数据的方式对曲线拟合,通过方差分析曲线的拟合程度。
板料冷弯成形回弹量变化拟合曲线如图8所示,由图8可知,曲线拟合误差不超过0.2%,对板料回弹影响显著的因素依次为上模下压量、下模开口量、上模下行速度和摩擦因数。上模下压量和下模开口量与回弹量呈线性关系,上模下行速度和摩擦因数与回弹量呈指数关系。

图8 各因素对回弹影响的拟合曲线
对回弹公式(10)进行修正,得到式(12)。

式中:∆为优化后回弹计算值;∆0为优化前回弹理论值;为综合影响因子;k为上模下压量影响因子;k为下模开口量影响因子;k为上模下行速度影响因子;k为摩擦因数影响因子。
根据图8的拟合曲线,可以得到各影响因子的计算见式(13)。
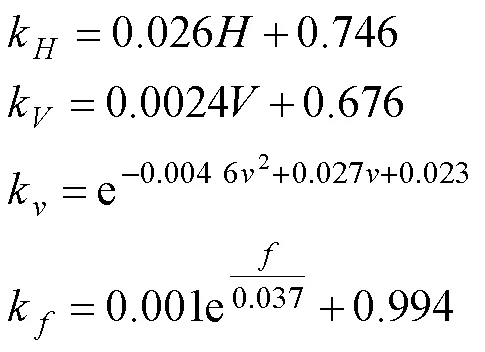
4.2 试验验证
为验证所构建的冷弯回弹曲线方程的精度,在JCOE成形机上,选择尺寸规格分别为10 mm× 300 mm×1 800 mm、20 mm×450 mm×1 800 mm、30 mm×600 mm×1 800 mm的316L不锈钢进行多道次冷弯实验。
在多道次冷弯过程中,板料清洁平整不需做任何润滑处理,在接触区增加不同粗糙度的垫片来改变摩擦因数;在板料弯曲中心和直边端点安装发光标靶,采用发光成像仪记录位移变化并记录回弹量,求取平均值。多道次冷弯后样品如图9所示,径壁比值≤10。
针对试验使用的3种板材规格分别进行有限元回弹模拟和理论计算。图10为冷弯回弹测量平均值与模拟值、计算值的对比情况。当板厚为20 mm时,模拟值、计算值和实测值数据吻合较好;当板厚为10 mm时,弯曲回弹模拟值偏差最大,但不大于5.5%。从图10可以看出,理论计算值更接近于测量值,这主要是由于优化后的理论模型综合考虑了诸多关键影响因素的耦合作用,更接近于真实弯曲工况。

图9 JCOE成形试验回弹测定
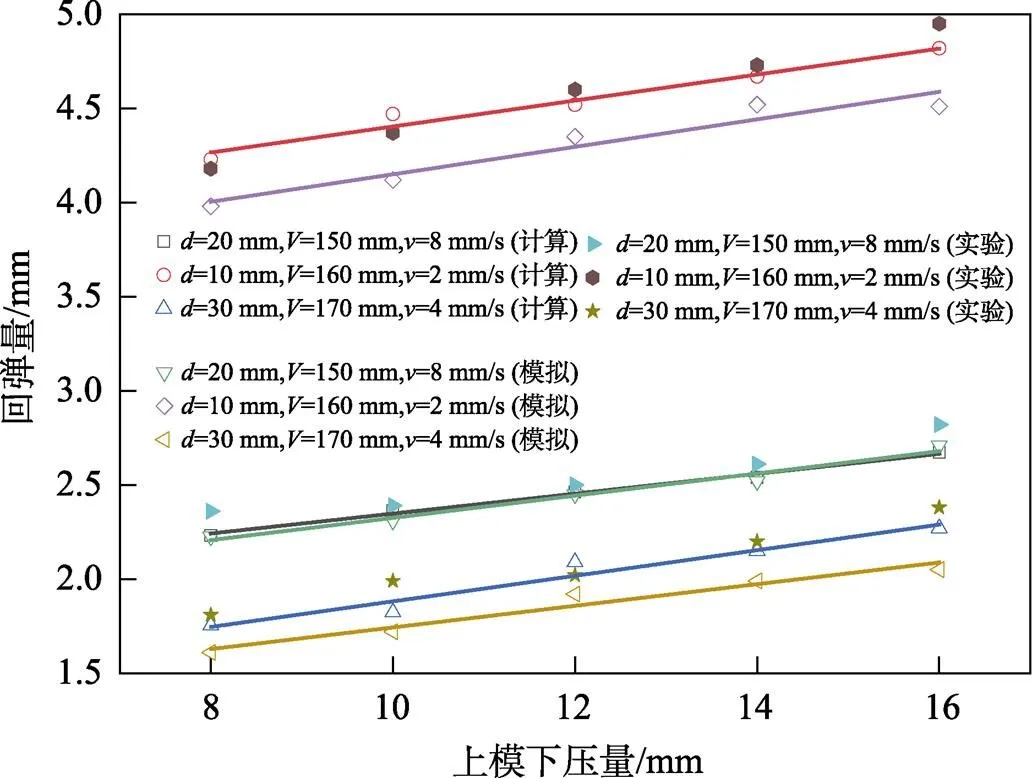
图10 回弹对比
5 结论
1)基于宽板弯曲回弹理论,根据板料不同弯曲初始阶段、弹塑性变形阶段和塑性变形阶段的应力–应变分布特征,综合材料固有性能和板料几何参数对回弹的影响,利用反弯矩及塑性变形条件,推导并建立了理想状态下的冷弯回弹方程。
2)针对316L奥氏体不锈钢直缝焊管JCOE生产技术,对该类板材的弯曲工艺过程进行深入研究。采用有限元仿真技术研究影响板材弯曲质量的因素,包括材料本身内在性能、上模下压量、上模下行速度、下模开口量以及摩擦工况等对弯曲变形区应力分布、回弹分布以及最大回弹量的影响规律,阐明板料回弹变化特征,获得了径壁比值≤10时板料最佳冷弯成形工艺参数,即上模下压量为12 mm,下模开口量为150 mm,上模下行速度为4 mm/s,摩擦因数为0.15。
3)有限元模拟结果表明,回弹量与上模下压量、下模开口量呈线性关系,与上模下行速度、摩擦因数呈指数关系。综合考虑影响回弹的主要工艺参数变化特征,对理想状态下的冷弯回弹方程进一步优化,并在JCOE试验机上进行多道次冷弯试验,回弹计算结果与实测结果吻合较好。因此,构建的冷弯回弹方程可以为同类焊管冷弯质量控制提供重要理论基础。
[1] LIU Yi-ke, ZHU Wei-lin, MI Li-jun, et al. Migration of Multiples from the South China Sea[J]. Science China Earth Sciences, 2015, 58(3): 482-490.
[2] 曾晓光, 金伟晨, 赵羿羽, 等. 海洋开发装备技术发展现状与未来趋势研判[J]. 舰船科学技术, 2019, 41(17): 1-7.
ZENG Xiao-guang, JIN Wei-chen, ZHAO Yi-yu, et al. Current Situation and Development of Marine Development Equipment Technology[J]. Ship Science and Technology, 2019, 41(17): 1-7.
[3] REN Q, ZOU T, LI D, et al. Numerical Study on the X80 UOE Pipe Forming Process[J]. Journal of Materials Processing Technology, 2015, 215: 264-277.
[4] PHANITWONG W, BOOCHAKUL U, THIPPRAKMAS S. Design of U-Geometry Parameters Using Statistical Analysis Techniques in the U-Bending Process[J]. Metals, 2017, 7(7): 235.
[5] ZHAO J, LI Jian, QU Xiao-yang, et al. Study on Intelligent Control Technology for Forming Steel Pipe of Pipeline with JCO Process[J]. Science China (Technological Sciences), 2011, 54(10): 2754-2759.
[6] GATTMAH J, OZTURK F, ORHAN S. Numerical Simulation of Bending Process for Steel Plate Using Finite Element Analysis[J]. Arabian Journal for Science and Engineering, 2019, 44(12): 10285-10292.
[7] POURBOGHRAT F, CHU E. Springback in Plane Strain Stretch/Draw Sheet Forming[J]. International Journal of Mechanical Sciences, 1995, 37(3): 327-341.
[8] PADGHAN N, DESHPANDE P, SAKHALE C. Force Analysis of Metal Sheet in Bending Operation on Sheet Bending Machine[J]. International Journal of Engine Research, 2015, 4: 267-270.
[9] 刘克进. 薄板冲压回弹试验研究及数值模拟对比分析[D]. 长沙: 湖南大学, 2004: 34-53.
LIU Ke-jin. Experimental Study on Springback and Its FEM Simulation Contrast in Sheet Matal Forming Process[D]. Changsha: Hunan University, 2004: 34-53.
[10] SU C, ZHAO J, GUO S. Analytical Description of Intelligent Controlled U-Free Bending Process in Wide Plate[J]. Materials Research Innovations, 2015, 19(5): 726-733.
[11] 马海宽, 李培力, 隋健, 等. JCOE预弯成型工艺理论分析与有限元计算[J]. 化工设备与管道, 2014, 51(3): 65-69.
MA Hai-kuan, LI Pei-li, SUI Jian, et al. Theoretical and Finite Element Analysis for JCOE Pre-Bending Forming Process[J]. Process Equipment & Piping, 2014, 51(3): 65-69.
[12] 范利锋, 梁培, 王葛, 等. 直缝焊管JCO成形非对称弯曲变形过程分析[J]. 塑性工程学报, 2020, 27(2): 94-101.
FAN Li-feng, LIANG Pei, WANG Ge, et al. Research on Asymmetric Bending Process of JCO Forming for Straight-Seam Welded Pipe[J]. Journal of Plasticity Engineering, 2020, 27(2): 94-101.
[13] 李聪, 赵宏伟, 孙琳琳, 等. 45号钢承载能力的原位三点弯曲试验研究[J]. 东北大学学报(自然科学版), 2019, 40(6): 869-874.
LI Cong, ZHAO Hong-wei, SUN Lin-lin, et al. Research on Load Capabilities of 45#Steel via In-Situ Three-Point Bending Tests[J]. Journal of Northeastern University (Natural Science), 2019, 40(6): 869-874.
[14] 鄂大辛. 金属管材弯曲理论及成形缺陷分析[M]. 北京: 北京理工大学出版社, 2016: 184-191.
E Da-xin. Metal Tube Bending: Theory and Forming Defects Anaiysis[M]. Beijing: Beijing Institute of Technology Press, 2016: 184-191.
[15] 马灿. 大直径厚壁管的成型技术[D]. 合肥: 合肥工业大学, 2010: 8-14.
MA Can. Forming Technology of Large-Diameter and Thick-Wall Tube[D]. Hefei: Hefei University of Technology, 2010: 8-14.
[16] WANG Jia-mei, ZHANG Le fu. Effects of Cold Deformation on Electrochemical Corrosion Behaviors of 304 Stainless Steel[J]. Anti-Corrosion Methods and Materials, 2017, 64(2): 252-262.
[17] 夏正文, 许全光, 马世龙, 等. 316L不锈钢焊管应变时效状态的耐晶间腐蚀性能研究[J]. 焊管, 2021, 44(8): 7-10.
XIA Zheng-wen, XU Quan-guang, MA Shi-long, et al. Intergranular Corrosion Resistance of 316L Stainless Steel Welded Pipe under Strain Aging State[J]. Welded Pipe and Tube, 2021, 44(8): 7-10.
[18] ÖRNEK C, ENGELBERG D. Towards Understanding the Effect of Deformation Mode on Stress Corrosion Cracking Susceptibility of Grade 2205 Duplex Stainless Steel[J]. Materials Science & Engineering A, 2016, 666: 269-279.
[19] FATHI H, EMADODDIN E, MOHAMMADIAN H R, et al. Effect of Punch Speed on the Formability Behavior of Austenitic Stainless Steel Type 304L[J]. Metals and Materials International, 2016, 22(3): 397-406.
[20] LIU B, VILLAVICENCIOC R, SOARES C G. Experimental and Numerical Analysis of Residual Stresses and Strains Induced during Cold Bending of Thick Steel Plates[J]. Marine Structures, 2018, 57(3): 121-132.
[21] 孔政, 张杰, 李洪波, 等. 摩擦系数对DP780钢拉深成形极限的影响[J]. 塑性工程学报, 2018, 25(2): 252-259.
KONG Zheng, ZHANG Jie, LI Hong-bo, et al. Effects of Friction Coefficient on the Deep-Drawing Forming Limit of Dual-Phase Steel[J]. Journal of Plasticity Engineering, 2018, 25(2): 252-259.
Construction of Springback Curve Equation and Process Optimization of Welded Pipe during Cold Bending
ZHAO Yue-wei1, SHUAI Mei-rong1, CHU Zhi-bing1, GUI Hai-lian1, ZHAO Xiao-dong1, GAO Hong2, WU Li-hua3, ZHAI Li-li2
(1. Engineering Research Center of Heavy Machinery of the Ministry of Education, Taiyuan University of Science and Technology, Taiyuan 030024, China; 2. Wujin Stainless Steel Co., Ltd., Jiangsu Changzhou 213111, China; 3. Sinosteel Stainless Steel Pipe Technology (Shanxi) Co., Ltd., Taiyuan 030600, China)
The work aims to study the bending unloading springback and stress distribution characteristics of 316L austenitic stainless steel plate JCOE and impose corresponding compensation to pre-bending value, to improve the bending accuracy. Based on the elastic-plastic deformation theory, the effects of key forming parameters on plate bending and unloading springback were studied by finite element simulation method. The equation of springback curve was also established through linear/nonlinear fitting and superposition of affecting parameters. The springback had a linear relationship with the displacement of upper mold and the opening degree of lower mold, but had an exponential relationship with the speed of upper mold and the friction coefficient. The optimal parameters are as follow: the displacement of upper mold is 12 mm, the opening degree of lower mold is 150 mm, the speed of upper mold is 4 mm/s, and the friction coefficient is 0.15. The calculated bending springback value is in good agreement with the measured average value for the plate with diameter-wall ratio ≤10. The established model can provide a theoretical foundation for the practical production.
cold bending of welded pipe; springback analysis; construction of springback equation; optimization process
10.3969/j.issn.1674-6457.2022.07.014
TG316
A
1674-6457(2022)07-0098-08
2021–11–29
国家自然科学基金(U1710113);常州市领军型创新人才引进培育项目(CQ20200042);山西省重点研发计划(201903D121043);山西省研究生教育改革研究课题(2020YJJG241)
赵月伟(1996—),男,硕士生,主要研究方向为金属弯曲成形。
帅美荣(1978—),女,博士,教授,主要研究方向为金属塑性变形理论与技术。
责任编辑:蒋红晨

