行数为2的变换图的若干性质

金晶晶

（福建船政交通职业学院 通识教育学院，福建 福州 350007）

但由于U(R,S)的复杂性，关于变换图G(R,S)性质和结构刻画的研究较少。变换图G(R,S)的性质是Brualdi 猜想研究的重要工具。为了深入研究变换图G(R,S)的性质，本文研究了行数为2 的变换图G(R*,S*)，其中，R*=(r1,r2)且S*=(1,…,1)。

1 主要结果

对于行数为2的变换图G(R*,S*)，若a1j= 1，则a2j= 0，j= 1,2,…,n；反之亦然。这就意味着A完全由第一行来决定。显然，A的第一行A′是包含r1个“1”和n-r1个“0”的行向量；行数为2的变换图G(R*,S*)是变换图G(R,S)的子图，G(R*,S*)的矩阵类U(R*,S*)是G(R,S)的矩阵类U(R,S)的2 × 2 子矩阵类，G(R*,S*)局部刻画了G(R,S)的性质和内在结构。定义H(r,n)为所有由“0”和“1”组成的n维行向量的集合，其中r( ≥1)表示每个n维行向量中“1”的个数，显然，H(r,n)中每个n维行向量中“0”的个数为n-r。设B∈H(r,n)，B的一个变换是指将B的一个形如(0,1)（或(1,0)）的子向量替换成(1,0)（或(0,1)）的一个作用。G(r,n)定义为这样的一个无向简单图：其点集是H(r,n)，H(r,n)中的两个n维行向量是相邻的，当且仅当其中一个n维行向量可以由另外一个n维行向量经过一个变换得到。比较G(R*,S*)与G(r,n)的定义，可得：

定理1G(R*,S*)与G(r,n)是同构的，其中R*=(r1,r2)且S*=(1,1,…,1)，r=r1，n=r1+r2。

因此，只要研究G(r,n)的性质就可得到G(R*,S*)的相应性质。

定理2G(r,n)同构于G(n-r,n)。

证明G(r1,n1)的顶点v所对应的行向量是n1维的，将它扩大为n2维行向量v′，v′与v在第1至第n1位置上的元素相同，v′在第n1+ 1,n1+ 2,…,n1+r2-r1位置上的元素都是“1”，而在第n1+r2-r1+ 1,n1+r2-r1+ 2,…,n2位置上的元素都是“0”。记由这些v′所生成的图为G′(r2,n2)，不难看到，G′(r2,n2) ≅G(r1,n1)，且G′(r2,n2) ≅G(r2,n2)。

定理6 的逆一般不成立。例如，G(1,6)是一个6 阶完全图，而G(2,4)是一个6 阶非完全图，所以与G(1,6)中的某个子图同构，但是，2 ＞1。

另外，G(r,n)有较好的连通性，G(r,n)的连通度等于其最小度r(n-r)[3]；G(r,n)是哈密尔顿图[5]。

2 几类变换图的作图

下面，根据变换图的性质，对变换图G(1,4)、G(2,4)、G(2,5)和G(2,6)进行作图.用G[C]表示G(r,n)的点集的一个子集C的生成子图。称C为G的一个团，当且仅当G[C]为完全图。称G(r,n)中点数最多的团为最大团。若G(r,n)中的一个顶点所对应的行向量在i1,i2,…,it位置上的元素为“1”，其余位置上的元素全为“0”，则将该顶点记为vi1,i2,…,it，则变换图G(1,4)、G(2,4)、G(2,5)分别为图1～3：

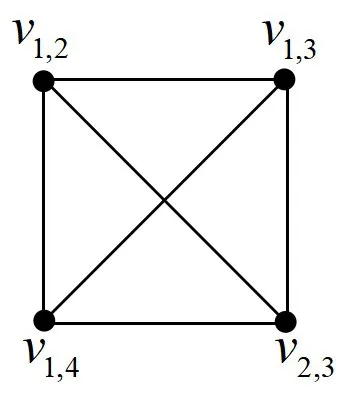
图1 变换图G(1,4)Figure 1 Interchange graph G(1,4)

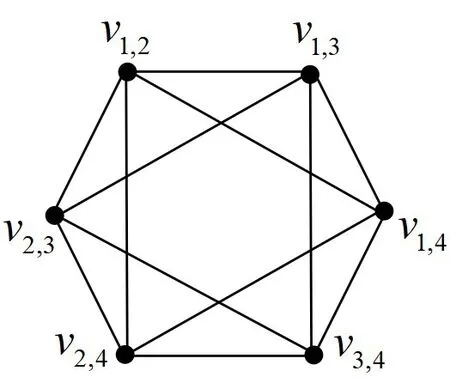
图2 变换图G(2,4)Figure 2 Interchange graph G(2,4)

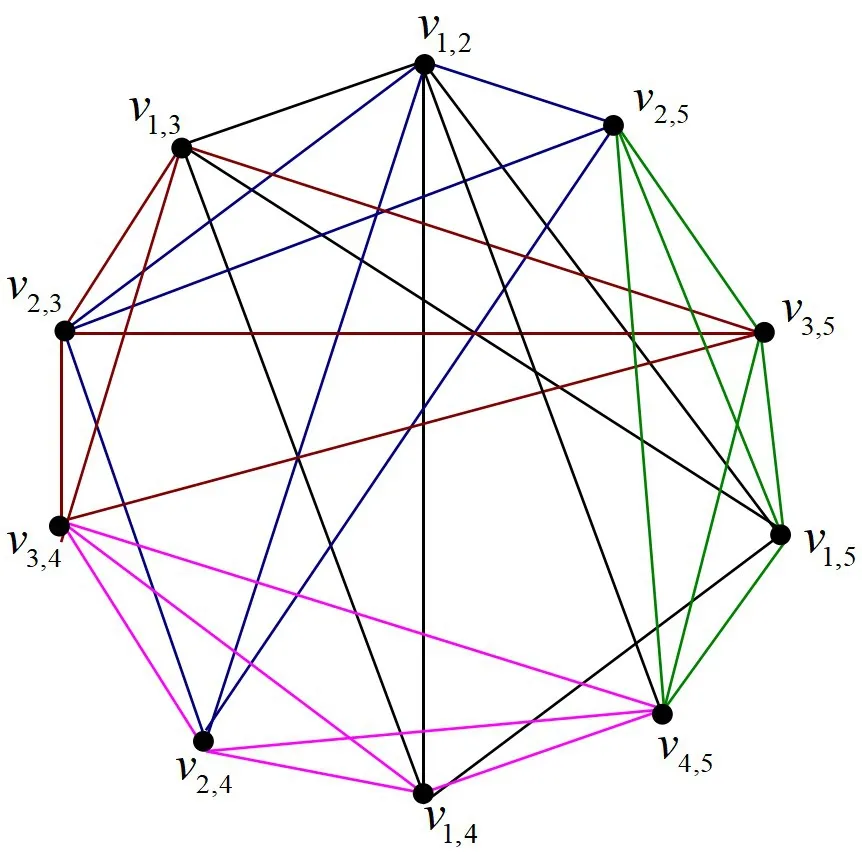
图3 变换图G(2,5)Figure 3 Interchange graph G(2,5)

由图1～3 可见，G(1,4)是完全图；G(2,4)有8 个最大团，每个最大团的顶点数为3；G(2,5)有5 个最大团，每个最大团的顶点数为4。

下面，利用变换图的性质和递归构造方法对G(2,6)进行作图。根据定理3，G(2,6)是8正则的，且其顶点数为V(G(2,6)) = 15，分别是v1,2、v1,3、v1,4、v1,5、v1,6、v2,3、v2,4、v2,5、v2,6、v3,4、v3,5、v3,6、v4,5、v4,6、v5,6，边数E(G(2,6)) =60。G(2,6)共有6 个最大团：C1={v1,2,v1,3,v1,4,v1,5,v1,6}，C2={v1,2,v2,3,v2,4,v2,5,v2,6}，C3={v1,3,v2,3,v3,4,v3,5,v3,6}，C4={v1,4,v2,4,v3,4,v4,5,v4,6}，C5={v1,5,v2,5,v3,5,v4,5,v5,6}，C6={v1,6,v2,6,v3,6,v4,6,v5,6}。每个最大团的顶点数是5，边数是10，且每个顶点都包含在2个最大团中，每条边恰包含在1个最大团中。基于以上讨论，按照变换图G(2,6)的最大团构造，先画出最大团C1={v1,2,v1,3,v1,4,v1,5,v1,6}，再依次按照最大团C1、C2、C3、C4、C5、C6对G(2,6)进行作图。

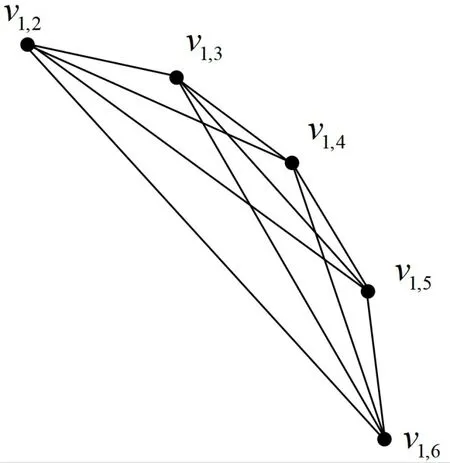
图4 变换图G(2,6)中的最大团C1Figure 4 The maximum clique of interchange graph G(2,6)

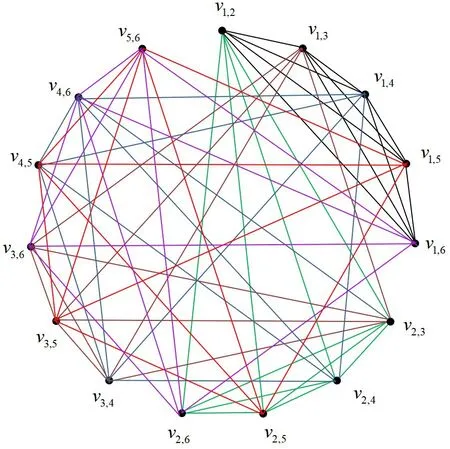
图5 变换图G(2,6)Figure 5 Interchange graph G(2,6)

综上，变换图G(1,5)、G(2,7)和G(3,6)亦可按照其性质和最大团的递归构造进行作图，此处不再赘述。