基于PageRank模糊聚类的网络社团挖掘

马丽娜

(西安财经大学行知学院，经济与统计学院， 陕西,西安 710038)

0 引言

近年来涌现出许多网络社团挖掘(也称为社团发现)算法[1-2]，从数学意义上来看，复杂网络中的社团划分是对具有连接相似关系的节点进行的聚类[3-4]。基于类原型的聚类算法，例如c均值聚类、模糊c均值(FCM)等，已在网络社团挖掘中得到广泛应用[5-6]，但是这些聚类方法的结果易受初始种子节点的影响，实验结果不稳定，并且需要事先给定网络社团个数。本文提出一种基于PageRank重要度和模糊c均值聚类的社团发现算法。该算法可以视为一种适用于网络数据的改进FCM算法。首先，根据节点的PageRank值确定种子节点候选集，利用相似性阈值和最大最小模块度自适应确定社团个数和最优种子集合。用谱映射的思想将网络数据映射成特征空间上的向量数据，进而实施模糊c均值聚类，得到节点所属各个社团的隶属度值。在真实网络上的数据实验证明了所提出算法的有效性。

1 相关理论

1.1 模糊C均值聚类

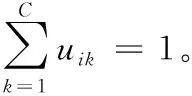
(1)

其中，m为控制模糊划分的权重参数，一般设为2,dik为数据xi到簇k的欧式距离。

(2)

(3)

不断更新每个簇的簇中心vk(k=1,2,…,C)和隶属度矩阵U，使得目标函数达到最小，可得到最优划分。

1.2 网络重要度和模块度

PageRank是一种常用的网络重要性度量，计算式为

(4)

其中,Na为所有指向a的网页的集合，Kb为网页b指向的网页个数。

最大最小模块度是一种常用的衡量网络社团划分准确率的指标，其定义如：

Qmax-min=Qmax-Qmin=

(5)

其中

(6)

Cx表示节点x所在的社团

(7)

(8)

(9)

模块度函数值越大，对应的社团划分结果与网络真实的社团结构越接近。

2 基于RangRank的聚类社团挖掘

2.1 网络初始种子选取

将复杂网络中的节点看成网页，那么节点的重要性就相当于节点所对应的PageRank值的大小。但种子节点的选择不仅要看节点的PageRank值，还要依据节点之间的差异性。节点之间的相似性定义为

(10)

其中，nij为节点i和节点j的公共节点数，ki、kj分别为节点i和节点j的度。

首先将节点按PageRank值大小降序排列，把PageRank值后25%的节点从种子节点候选集中去掉。预先设置一个相似性阈值，选择PageRank值最大的节点作为第一个种子节点，然后计算PageRank值次大节点和PageRank值最大节点之间的相似性。如果这个相似性的值小于预先设置的阈值，则将该节点加入到种子节点集中。以此类推，直到选出来的前75%的节点集中没有节点满足设定的相似性阈值就结束算法。通过不断的调整相似性的阈值，可以得到不同数量的种子节点集，从而得到所有可能的初始的种子节点集。

2.2 谱映射

设网络的邻接矩阵为

A=(aij)n×n

(11)

其中，当节点i和节点j相连时，aij=1；否则，aij=0。记对角矩阵为

D=(dii)

(12)

其中，dii=∑aik表示与节点i相连的节点数量。谱映射的数据转换过程如下：

(1) 计算Ax=tDx的n个特征向量；

(2) 取这n个特征向量的前k-1维，并将其标准化；

(3) 标准化的k-1维特征向量代表原始网络中的节点。

2.3 基于RangRank的聚类算法

设相似度阈值的集合为A=(A1,A2,…,An)，令M0=0,i=1，初始的社团划分记为U。基于PageRank的聚类算法记为PFCM，算法具体流程如图1所示。

3 实验

选取2个真实的网络数据Karate和Football来验证PFCM算法的高效性，表1列出了真实网络的数据。

表1 真实网络的节点与边

3.1 Karate网络

对Karate网络数据进行PFCM算法社团划分，不同社团数量所对应得最大最小模块度值如图2所示。

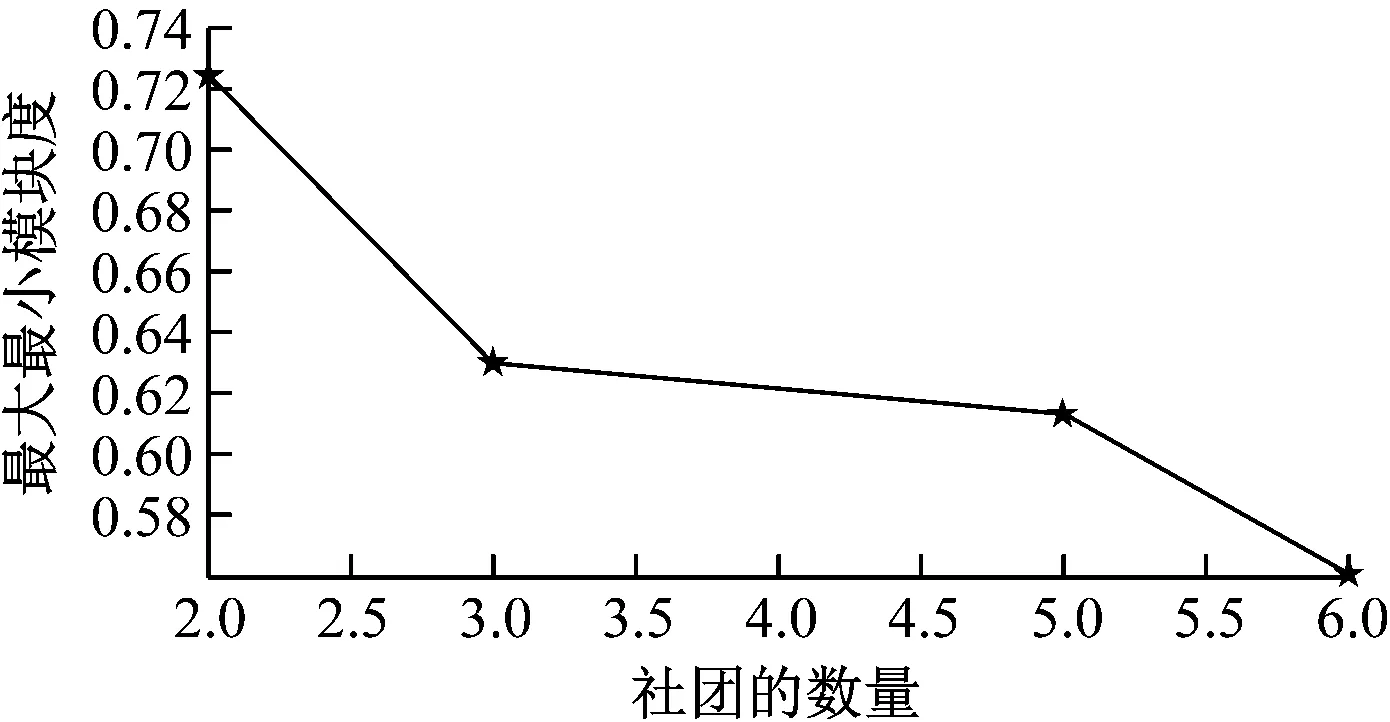
图2 Karate网络不同社团数量对应的最大最小模块度值

图2横坐标是社团的数量，纵坐标是最大最小模块度值。从图2中可以看出最大的最大最小模块度所对应的社团的数量是2，这与Karate网络的真实社团划分相符。

应用标准互信息(NMI)、精确度(precision)、召回率(Re-call)和兰德指数(RI)这4个评价指标，对FCM和PFCM算法的社团划分结果进行评价，如表2所示。PFCM算法除Precision外，在其他3个指标(NMI、Recall、RI)上均优于FCM算法，而Precision值两算法的结果相差不大。FCM算法对Karate网络进行100次实验所得结果的NMI的平均值为0.033，社团划分结果很不理想。PFCM算法结果的Recall较FCM算法提升了40.4%，RI提升了40.9%。从上述结果综合来看，PFCM算法优于FCM算法。

表2 Karate网络数据聚类效果评价指标对比

3.2 Football网络

对Football网络数据进行PFCM算法社团划分，不同社团数量所对应得最大最小模块度值如图3所示。

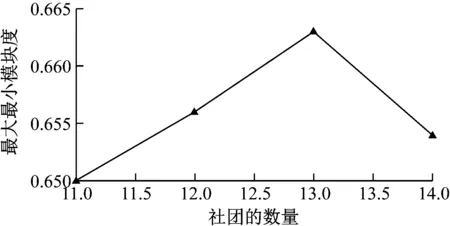
图3 Football网络不同社团数量对应的最大最小模块度值

由图3可以看出，最大的最大最小模块度值所对应的社团的数量是13。表3列举了4种不同的评价标准对FCM算法和PFCM算法在Football网络上实验所得结果的对比，FCM算法的4个评价指标是100次实验结果的平均值。

表3 Football网络数据聚类效果评价指标对比

由表4可以看出，PFCM算法结果的NMI较FCM算法提升了34.6%，Precision提升了12.8%，Recall 提升了100%，RI提升了8.06%。

3.3 算法稳定性对比分析

PFCM算法和FCM算法在真实网络Karate和Football上进行了100次实验。图4展示了前5次实验的结果(100次实验结果呈现的趋势与前五次类似，为了展示方便图中只展示了前五次的结果)，2个子图的横坐标表示算法进行实验的次数，纵坐标表示的是标准互信息(NMI)的值。

图4中的红色的线是PFCM算法的实验结果，实验结果非常稳定。蓝色的线是FCM算法的实验结果，不同次实验得到的NMI的值不同，波动非常大，实验结果的精确度具有随机性。同时PFCM算法实验结果的NMI值普遍要高于由FCM算法的NMI值。这验证了PFCM算法不仅解决了FCM算法的实验结果受初始的种子节点的影响的缺点，而且算法的精确度高。

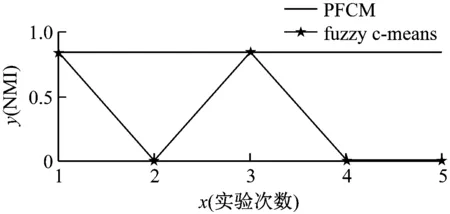
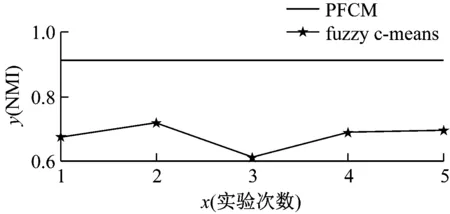
图4 PFCM算法和FCM算法的比较

4 总结

本文提出了一种改进的FCM算法(记为PFCM)，解决了传统FCM算法受初始种子节点和需要事先给定网络社团个数的问题。引入PageRank和最大最小模块度确定网络最优社团数量，利用谱映射方法将网络邻接矩阵转换为向量空间上的数据，进而执行FCM算法实现网络社团划分。在真实网络上的数值实验表明，PFCM算法在准确性与稳定性上都有了明显提升。