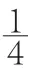合理运用多元表征，有效实现深度学习

北京市石景山区先锋小学 李小红

在平时的数学教学过程中，常用的表征方式主要有以下几种：图形表征、文字表征、语言表征和符号表征。实践研究表明，使用多种不同的表征方式可以帮助学生拓展思路，有利于学生构建良好的知识结构，便于加深学生对数学知识的理解。多元表征注重数学学习对象多样化呈现，教学中，教师应指导学生深入研究问题，关注问题的多元表征，以促进数学知识的多元建构，从而让学生的数学学习深度发生。

一、注重数学学习对象多样化呈现，促进数学知识多元建构

数学学习对象包括空间与图形、数学概念、数量关系、数量间运算和问题解决等。在平时的教学中，学习对象呈现方式应多样化，既要有言语和文字的，也要有数字符号的，还要有直观图形的，这样方能凸显数学学习对象多元属性，便于学生将数学信息进行多通道输入，从而实现数学知识的多元表征、数学意义的多元建构。

在小学数学教学中，如果教师仅提供符号化、形式化的抽象表征，对于基础薄弱的学生而言，在理解抽象的数学知识方面存在一定困难，因此会导致这部分学生抵触对数学的学习，甚至失去学好数学的信心。如果教师在教学中巧用数学多元表征，并利用不同表征可以转换和互相补充的作用，就可以让学生从不同的角度认识数学对象，使学生对数学原理和数学概念的理解更为深刻，有助于学生由具体思维向抽象思维的发展，促进数学知识间的多元建构。

笔者在教学“推理”一课时，有这样一道题：有语文、数学和品德与生活三本书，小红、小刚、小丽各拿一本，小红拿的是语文书，小丽没拿数学书。小刚拿的是什么书？小丽呢？学生通过思考，用多种方式表示出了对于这道题的理解，学生想到了如下几种表达方式。

文字表征：已经知道小红拿的是语文书，又知道小丽没拿数学书，肯定小丽拿了品德与生活书，那么，小刚拿的一定是数学书。

连线表征，如图1。

图1

图表表征，如图2。

图2

教学中，通过这样的多元表征形式，既可以帮助学生加深对数学知识的认识与理解，又不增加学生认知负荷，让学生的经验充分展现，从而激活思维，实现了数学知识的多元表征、数学意义的多元建构。

二、寻找知识间关联，实现学生数学思维可视可感

借助数学多元表征，建构数学各种表征的联系，让学生的数学思维可视可感，有效帮助学生准确理解和把握数学知识的本质内涵和外延，渗透模型思想。

“乘法分配律”是人教版小学数学四年级下册的内容，因为定律的结构特征相对复杂，因此乘法分配律是数学教学中一个较难掌握的知识。乘法分配律将乘法与加法联系了起来，两种运算均有，用语言描述，讲法拗口；用字母表达，结构复杂，学生记忆时自然就增加了难度。学生如果记不住（或容易忘记）定律结构就难以做到灵活运用，遇到变式，当然更难以应对。可见，如何使学生清晰地建构乘法分配律的结构（数学模型），而且将其有效地储存于大脑中不遗忘，这是一个关键点。在教学中，笔者利用数学多元表征帮助学生建立模型，沟通理解知识间的关联，适当提升以拓宽学生思维，促进学生对于知识的深度理解。

（一）沟通知识间关联

1.借助面积模型理解乘法分配律

图形表征，如图3。

图3

文字表征：大长方形面积等于两个小长方形面积和。

算式表征：（5+4）×6=5×6+4×6。

通过让学生观察和对比，建立起三种表征间的联系，使学生思维可视可感。

2.多角度观察构建知识间联系

通过算式（5+4）×6=5×6+4×6，既能发现（5+4）个6等于5个6加4个6，等式两边都表示9个，还可以从不同角度找到不一样的几个几，如图4。

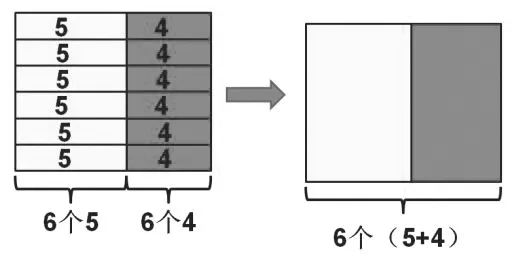
图4

观察上图的图形表征，通过分析可以得出：从左往右观察是6个（5+4），从上往下看是6个5和6个4之和。不管怎样看，都可以和乘法分配律建立起联系。

（二）猜想引发深度思考

为了拓展提升学生思维能力，教师可以尝试询问学生：如果把括号里面两个数的和变成两个数的差或三个数的和，你将有什么发现？从而引出更深层次的思考与想象，让学生发挥自己的能力，展开新的自主猜想，举例说明并验证……在学生表征过程中，进一步丰富学生对于乘法分配律的认识与理解，从而实现数学中的深度思考。

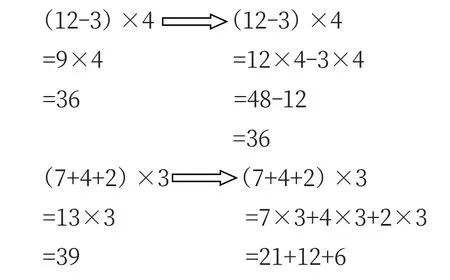
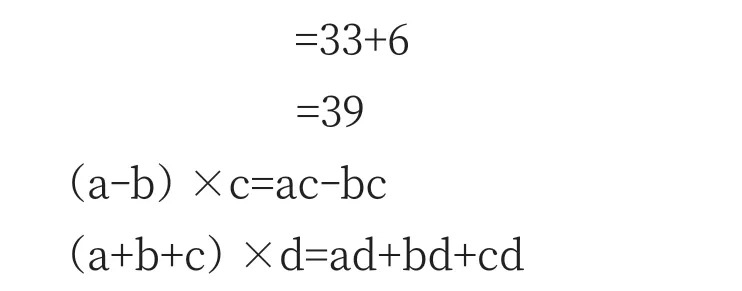
将多元表征渗透到数学教学课堂中，可以促进数学知识的理解与沟通，培养学生数学思维，引发学生深度思考，促进学生数学智慧生长。

三、帮助学生理解概念，促进数学知识多元建构

小学数学基础知识的一项重要内容是数学概念，学生理解数学知识的首要条件就是掌握数学概念，计算和解题的重要前提是理解数学概念，它是整个数学知识结构的基础，是基础知识的起点及逻辑推理的依据、数学方法的载体，是正确、合理、迅速进行数学运算的保证。在数学课堂中运用多元表征，能帮助学生从多角度深入理解数学概念的本质，使数学概念变得可视可感，有利于学生把握概念的理解，有利于建构知识体系。

小学低年级学生正处于具体形象思维水平阶段，因此在概念建构时，学生不仅要清楚相关概念的文字描述，更要体现在思维发展和认知完善的过程中。在概念教学中，学生理解概念时应该从具体出发，让学生多角度、多感官体验，然后再从具体表象中抽象概念内涵，这时的抽象是理解后的，这也是学生对于概念建模的过程。借助数学多元表征可以帮助学生从多角度深入理解数学概念的本质，提升概念教学的实效性，发展学生的数学深度思维能力。

“倍的认识”是人教版三年级上册第五单元的内容，“倍”是小学数学中比较抽象的概念，又是很重要的概念，“倍”的含义对于学生来说比较抽象，不容易理解。“倍”的概念的建构，不仅需要将“几倍”和“几个几”建立联系，更需要借助多元表征方式之间的转换，帮助学生逐层建构“倍”的概念。

课上，教师为学生提供学具，创设一个开放的探究空间，让学生通过摆一摆、圈一圈、画一画、算一算等多种表征方式，借助多元表征方式自主探究两种萝卜之间的倍数关系。把抽象的新知识“倍”与学生掌握的“几个几”建立联系，从而帮助学生理解“倍”的含义。下面是学生课上的作品。

实物表征，如图5。

图5

图形表征，如图6。

图6

语言表征：如果把2个胡萝卜看成1份，红萝卜有这样的3份，是3个2，红萝卜的个数是胡萝卜的3倍。

算式表征：6÷2=3。

课上通过展示学生的摆法，帮助学生理解“倍”的含义，接着在展示学生圈画的方式时，加深对“倍”的理解，突出“倍”的本质。通过展示学生线段图的表达方式，抽象出“倍”的线段图模型，最后通过对学生除法算式的展示，沟通“倍”与除法的联系。学生在观察、交流、操作的过程中，经历了“倍”概念的形成过程，符合儿童“直观—半直观半抽象—抽象”的认知过程，理解“倍”的含义。建立了“几倍”与“几个几”的联系，发展了学生的概括能力。使学生对“倍”的理解不断深入，让学生在多样化的活动中理解“倍”，在对比与抽象中深化对“倍”的认识。同样的问题，不同的学生表征出来的形式是不同的，可以看出学生不同的认知风格和思维水平。

四、凸显认知风格与水平，促进深度思维与实践综合应用能力发展

如果说数学理解是数学知识不断建构联系的过程，那么数学表达就是实践应用和思维提升的过程。借助数学多元表征，建构数学各种表征的联系，让学生的数学思维可视可感，有利于发展学生数学实践综合应用的能力。

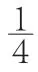
有的学生用具体直观形象的模拟图表征，有的学生则用线段图表征，其思维抽象水平高于模拟图表征的学生。有的学生用分数思想列式解答，有的学生用比的思想列式解答，还有的学生用方程思想列式解答。

图7

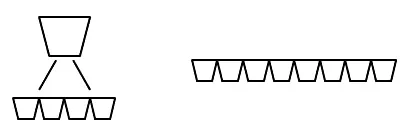
图8

小杯：840÷（4+8）=70ml 大杯：70×4=280ml

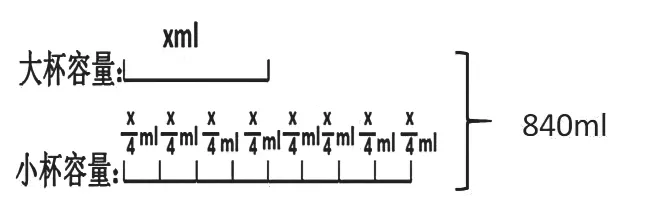
图9

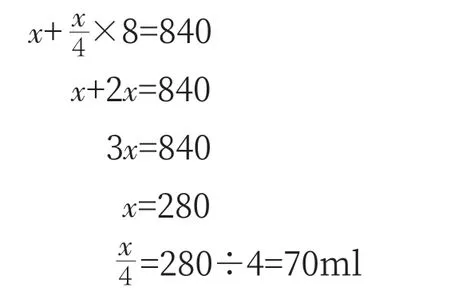
答：大杯容量为280ml，那么小杯容量为70ml。