基于改进快速探索随机树的复杂环境垂直泊车路径规划
徐远征 吴长水
(上海工程技术大学,上海 201620)
主题词:垂直泊车 路径规划 改进RRT算法 高斯分布采样 Reeds-Shepp曲线
1 前言
随着汽车保有量迅速增加,城市中车位不足、车位狭窄等问题日益突出。此外,常见的不规范停车行为使原来的单辆车位空间被两侧车辆占据,导致泊车场景更加复杂。开发适用于复杂环境的自动泊车系统是解决此类问题的关键。完整的自动泊车过程可分为感知、路径规划和控制执行3个部分,因此研究适用于复杂场景的泊车路径规划算法具有重要意义。
常见的泊车路径规划算法主要包括几何法与曲线拟合法。Plamen 等针对垂直泊车问题,结合杜宾斯(Dubins)曲线提出了基于最小转弯半径的无碰撞几何路径规划算法。李韬根据几何关系确定最短泊车路径与泊车起始区域,然后采用五次多项式进行了路径拟合,该路径满足车辆运动学约束。上述方法需对泊车区域进行详细的几何划分,且泊车必须从特定的点或区域进行,算法适用性及可拓展性较差。针对这一问题,部分学者利用快速探索随机树(Rapidly-exploring Randomized Tree,RRT)算法无需对泊车场景进行建模、适用性强的特点,提出了基于RRT 算法的解决方案。Lone等使用基本RRT算法进行垂直、水平及倾斜泊车的路径规划,然而其存在规划过程缓慢、路径不平滑等缺点。Seho 等通过指定RRT 种子取向加快规划速度,然而种子取向受泊车环境影响较大。
综上,为确保算法具有良好的适用性及可拓展性,本文充分利用RRT 算法的优势并对其进行改进,提出一种基于改进RRT 的垂直泊车路径规划算法,以满足任意初始位姿的路径规划需求。
2 车辆模型及泊车场景建模
2.1 车辆运动学模型
泊车是低速的运动过程(低于5 km/h),此时车辆可视为刚体,且车轮所受的侧向力可忽略,因此不会发生滑动,在实际研究过程中通常会对车辆运动学模型进行简化。基于此,本文以目标车位后端中点为世界坐标系原点,采用如图1所示的二自由度两轮车模型进行建模。
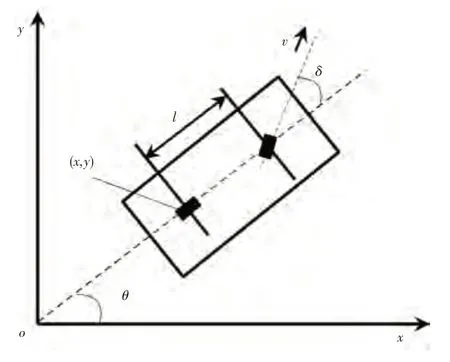
图1 车辆运动学模型
本文建立的车辆运动学方程为:

式中,()为车辆后轴中心点坐标;为后轴车速(向前为正);为轴距;为车辆航向角(逆时针方向为正);为等效前轮转向角(逆时针方向为正),其受最大等效前轮转角约束,满足||≤。
2.2 泊车场景设定
本文以城市普通垂直停车位为研究场景,综合考虑常见不规范泊车现象对泊车过程的影响,将泊车场景划分为有车位线场景及无车位线场景两类,如图2所示。
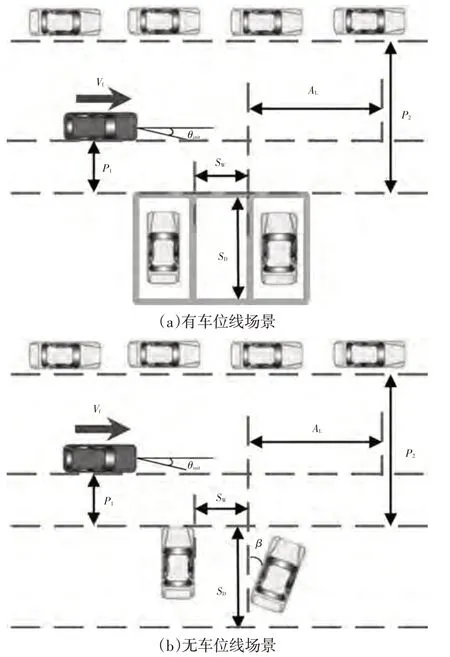
图2 泊车场景
对于有车位线场景,车位两旁的车辆对泊车过程没有影响,车辆可以车位线为参考进行标准泊车,目标泊车位置即为车位的中心。对于无车位线场景,车位两旁车辆占据了车位的部分泊车空间,此时车辆无法以车位线作为泊车参考依据,只能根据车位两旁车辆的停靠情况进行泊车。考虑到狭小空间内车辆泊入后驾驶员侧车门开启难的问题,本文规定当右侧车辆向右倾斜时,车辆泊入后应与右侧车辆保持平行。
本文制定的具体场景参数如表1 所示。根据国家标准车位尺寸以及实际泊车需求对车位基本尺寸进行了定义,考虑到车位两旁车辆对目标泊车位姿()的影响,本文对两旁车辆的倾斜角度进行了限定。若泊车场景参数满足上述设定的取值范围,则视为可泊车场景,否则视为不可泊车场景。最后,为使试验过程更贴合实际应用,本文对车身到车位前端的垂直距离、车辆初始航向角的取值范围进行了限定。
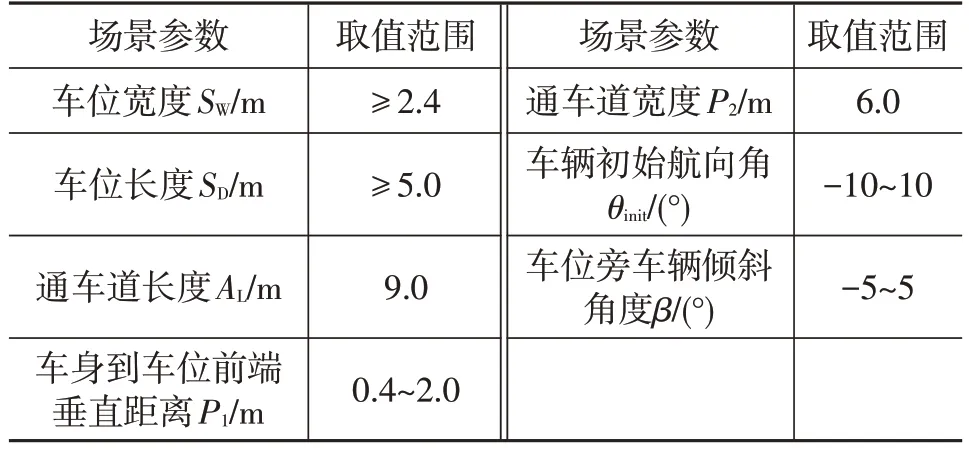
表1 场景参数
3 垂直泊车路径规划算法
3.1 基本RRT算法
RRT算法是一种使用增长树的搜索算法,其优势在于无需对泊车空间进行几何划分,若路径存在则可以满足任何初始位姿要求,且其可以满足车辆约束。基本RRT算法伪代码如下:

其中,为泊车起始点;为泊车目标点;为采样点;为与采样点最近的RRT 节点;为新的RRT节点;为采样次数;Δ为拓展步长;为到的最短距离;为RRT路径。
基本RRT 算法在应用于泊车路径规划时,在采样阶段存在采样点随机性大的问题,在拓展阶段存在不易通过狭窄通道、计算代价较大的问题,在路径生成阶段存在路径不平滑的问题。因此有必要对其进行改进。
3.2 改进RRT算法
在采样阶段,基于高斯分布及目标偏置采样,本文提出了一种融合采样方法加快采样速度。为解决拓展阶段的通道狭窄问题,本文使用逆向树生成新的RRT目标点,拓展过程中不断尝试用Reeds-Shepp(RS)曲线无碰撞连接该目标点。在路径生成阶段基于RS曲线对RRT 路径进行平滑优化。改进后的算法流程如图3 所示。
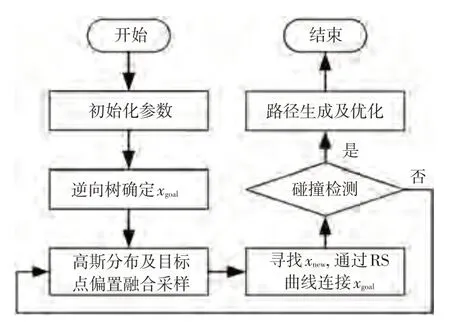
图3 改进RRT算法流程
3.2.1 融合采样方法
传统RRT 算法的采样点均匀分布在搜索空间中,存在过多的冗余搜索,导致算法效率较低。因此,本文融合高斯分布采样和目标偏置采样对其进行改进,利用高斯分布采样减少采样的随机性与盲目性,同时限制采样的方向及范围,使之更加符合车辆约束,采用目标偏置采样解决高斯分布采样存在的采样死区问题。采用的高斯分布采样表达式为:
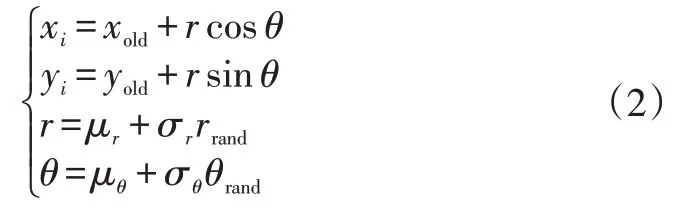
式中,x、y为当前第个采样点的横、纵坐标;、为当前采样点的父节点横、纵坐标;μ为当前采样点与父节点的相对距离;σ为采样区径向范围;μ为当前采样区中心线与轴的夹角;σ为采样区角度范围;(μ,σ)、(μ,σ)为随机数。
融合采样流程如图4所示。
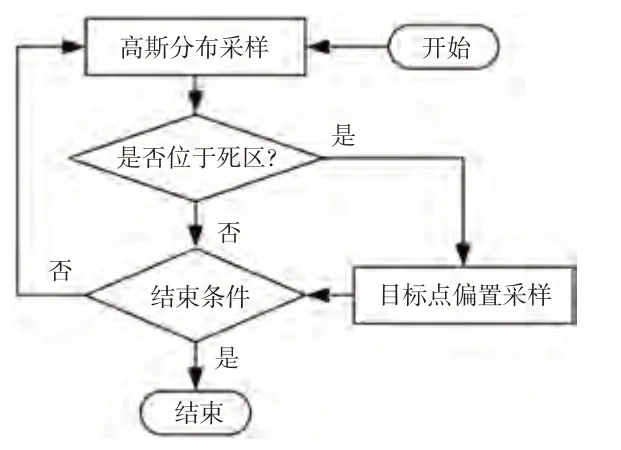
图4 融合采样流程
初始阶段,随机树顶点只有,采样区域中心线方向为当前车辆行驶方向;采样阶段随机树顶点数大于1个,此时采样区中心线方向为该节点与其父节点连线的方向。采样区中心线与轴的夹角μ为:
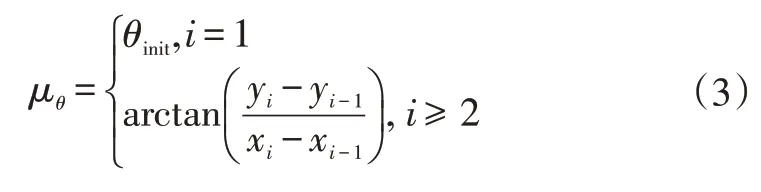
由于高斯分布采样具有一定的偏向性,其在采样过程中存在采样点落入死区的可能性,如图5所示。为确保采样过程的稳定性,当采样点落入死区时,采样算法将切换为目标点偏置,本文设置目标点偏置概率为0.1。
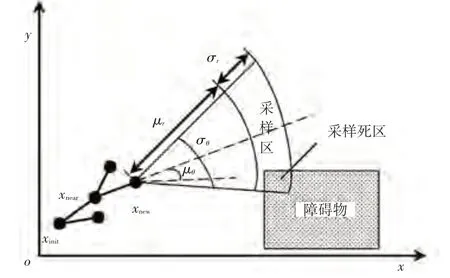
图5 采样区及采样死区
3.2.2 狭窄通道问题优化
由于车位较为狭窄,RRT拓展过程中存在狭窄通道难以进入的问题。此外,在复杂泊车环境下,由于RRT拓展的随机性,其规划的路径在车位内通常需要较多的位姿调整,容易造成车辆剐蹭等危险情况的发生。考虑到泊车过程中的安全性,应尽可能减少车辆在车位内的位姿调整。基于此,本文引入逆向拓展树及RS 曲线对RRT算法进行改进。
首先采用以固定步长沿直线生长的逆向拓展树调整RRT目标点,基本流程如图6所示。逆向拓展树的起始点为车辆最终的泊车位姿,终止点为车辆能够以最小转弯半径泊出且无碰撞的点,该点即为调整后的RRT目标点。在此基础上,在RRT树拓展的过程中,每当生成新节点时,直接将其用RS曲线连接到目标点,并对生成的RS 路径进行碰撞检测。若没有发生碰撞则RRT树拓展结束,将RS路径、RRT路径及逆向树路径合并为改进RRT 算法的初始规划路径;若发生碰撞,则RRT 树进行新一轮的拓展,直至能通过RS 曲线无碰撞地连接新节点与目标点。
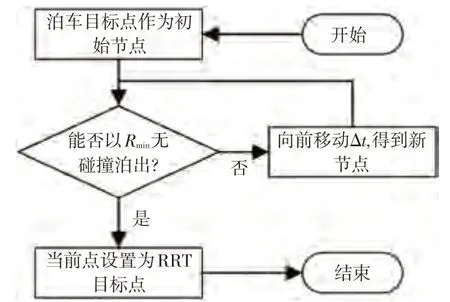
图6 RRT目标点迁移
RS 曲线以Dubins 曲线为基础,其假定车辆始终按照最小转弯半径进行转向且尽可能使用直线,起点到终点间的路径只由圆弧及直线构成。由于本文在规划过程中尝试采用RS 曲线对目标点进行直接连接,故最终在车位空间内的泊车路径将只由圆弧和直线组成,车辆在车位内没有多余的位姿调整,提高了泊车过程的安全性。
3.2.3 碰撞检测
为确保所规划路径的安全性,有必要对其进行碰撞检测。考虑到车辆和障碍物的几何形状均可抽象为矩形,本文采用方向包围盒(Oriented Bounding Box,OBB)检测方法,将碰撞检测转化为OBB 相交检测问题。其检测原理为:对于任意的2 个凸多边形物体,若能找到任意一个分离轴使这2 个物体在该轴上的投影不发生重叠,则判定2个物体之间不发生碰撞。
OBB检测原理如图7所示,4条中心线代表分离轴,矩形、分别代表车辆和障碍物。A、A为以A为坐标原点的局部坐标系下的单位向量,B、B为以B为坐标原点的局部坐标系下的单位向量。为矩形、中心点间的距离;为全局坐标系下的车辆航向角;为两矩形中心连线与全局坐标系轴的夹角。根据OBB 碰撞检测原理,只需判断2 个矩形在上述4 个分离轴A、A、B、B上的投影是否满足如下条件:
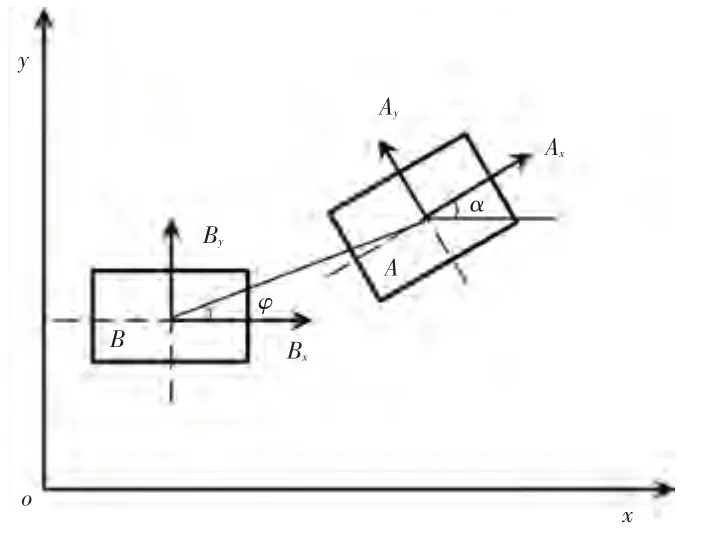
图7 OBB检测原理
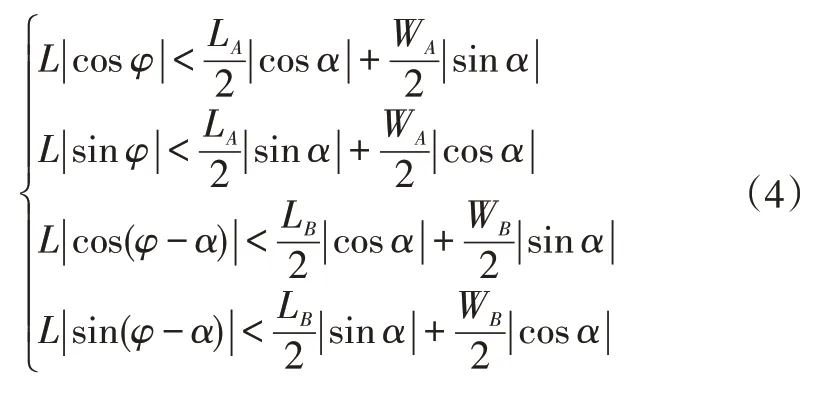
式中,L、L分别为矩形、的长度;W、W分别为矩形、的宽度。
如果同时满足式(4)中的4 个检测条件,即可判定车辆和障碍物发生碰撞。
3.2.4 路径优化
针对RRT 路径存在的曲率不连续、路径代价较大等问题,本文采用RS 曲线替换原有的RRT 路径,使优化后的路径能够满足车辆运动约束。当两点间不存在障碍物时,RS 路径即为最短路径,根据这一特性,本文基于贪婪思想,将每一段的局部最优路径进行合并,以此获得相对较小的路径代价。
路径优化过程如图8所示,本文以RRT路径索引的终点为优化起始点,根据索引编号由小到大依次通过RS 曲线连接优化起点与索引点,若在两点间能找到无碰撞的RS路径,则剔除两点间的其他索引点,并用新的路径替代原有的路径。然后以当前索引点为新的起始点进行下一轮优化,直至将原有的RRT 路径均转化为RS 路径。最后将优化后的RRT 路径进行合并,生成最终的垂直泊车规划路径。
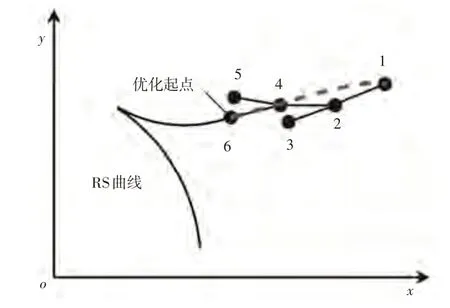
图8 路径优化
4 仿真分析
4.1 仿真参数设置
本文使用MATLAB 2020a 软件编写相应算法并进行仿真,并在相同的仿真条件下与基本RRT 及基于目标偏好的RRT(Goal-biasing RRT)算法进行比较。为验证算法的有效性及可拓展性,需测试车辆在不同初始位姿下的路径规划情况。本文采用批处理的方式,根据表1的场景参数所设计的测试用例如图9所示。其中车辆初始坐标范围为-5.2~5.2 m,步进0.4 m;车辆初始坐标范围为6.3~7.9 m,步进0.4 m;车辆初始角度范围为-10°~10°,步进10°。表2 所示为本文采用的车辆及车位参数。
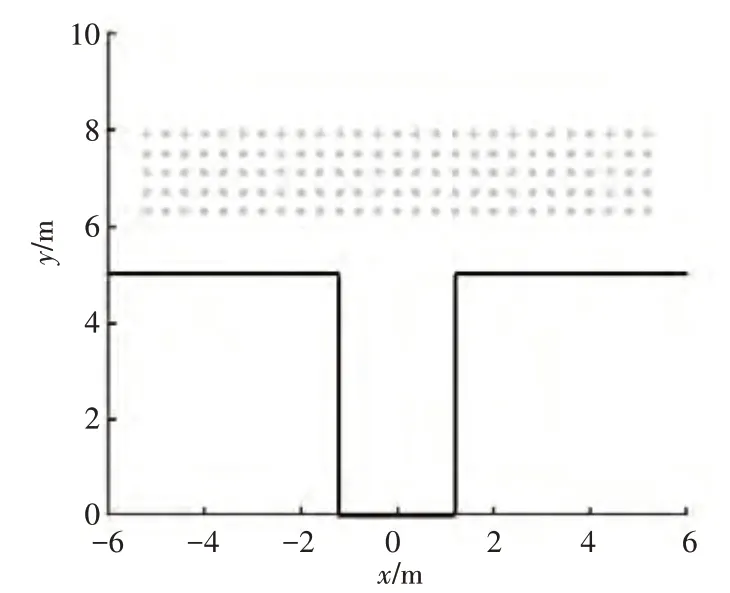
图9 测试用例
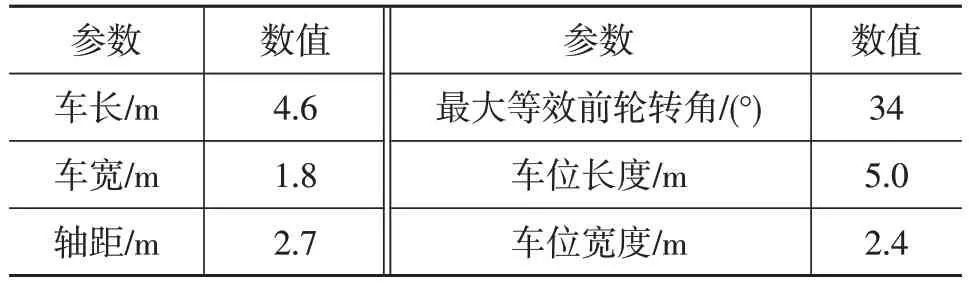
表2 车辆及车位参数
4.2 不同泊车场景下的路径规划结果
不同场景下的部分泊车路径规划结果如图10 所示。由图10 可知,不同泊车场景下所规划的路径均较为平滑,且车辆在泊车过程中的位姿调整较少。在泊车过程中车辆均能沿规划的路径泊入车位且与周围障碍物无碰撞,表明本文所设定的垂直泊车路径规划方法能够满足车辆及场景约束。此外,对于图10b所示的无车位线场景,车辆的最终泊车位姿在左、右两车的中间且车身与右侧车辆平行,确保了更大的车门开启空间,达到了预定的设计目标。
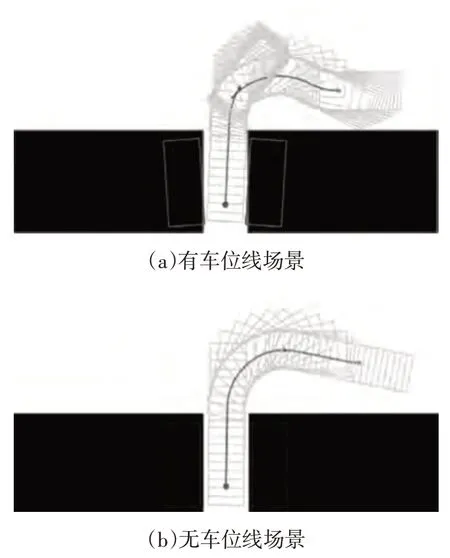
图10 不同泊车场景下的泊车路径
4.3 与RRT及其常见变体的比较
图11 显示了相同条件下基本RRT、Goal-biasing RRT与本文提出的改进RRT的路径规划情况。在采样次数方面,基本RRT和Goal-biasing RRT 采样次数多且有很多无效采样,而本文提出的改进RRT 算法采样次数改善较为明显,证明了本文提出的联合采样方法的有效性。在路径方面:基本RRT和Goal-biasing RRT 规划的路径不够平滑,且在车位内有较多的位姿调整,很难满足车辆运动及泊车安全的要求;改进RRT 规划的路径相对平滑,在本文提出的逆向生长树的作用下,车位内车辆无多余的位姿调整,有效提高了泊车过程的安全性。
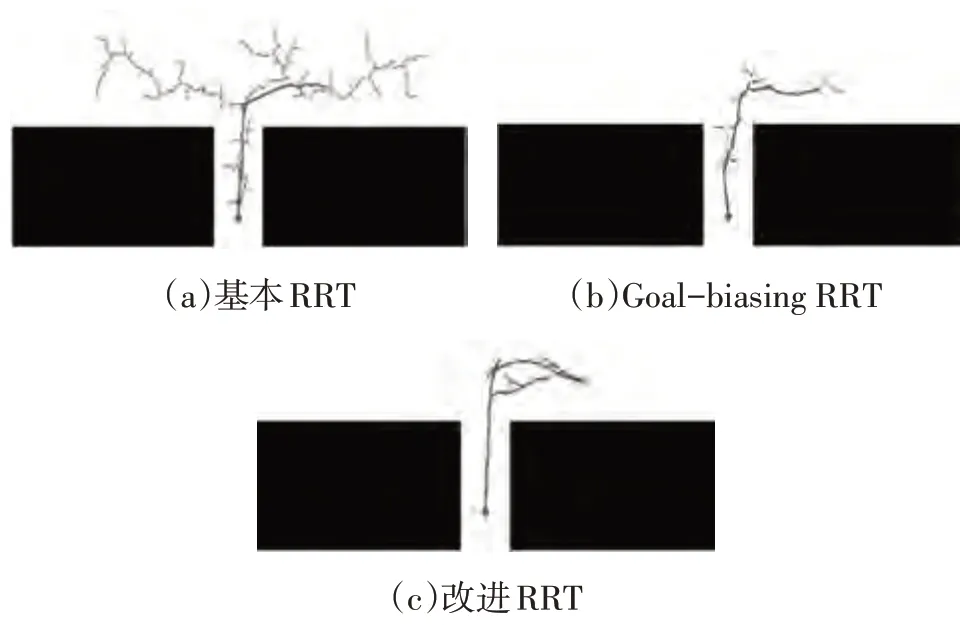
图11 不同方法的路径规划情况
批处理的平均时间、平均采样次数及路径代价如表3所示。由表3可知,在相同仿真条件下,基本RRT算法的消耗时间最长且路径代价最大,Goal-biasing RRT 相较于传统RRT 算法改进效果并不明显。相较于基本RRT 及Goal-biasing RRT,本文提出的路径规划方法平均规划时间分别缩短52.3%和41.7%,路径代价分别减少17.7%和13.9%,性能提升较为显著,证明了本文算法具有较好的适用性及可拓展性。
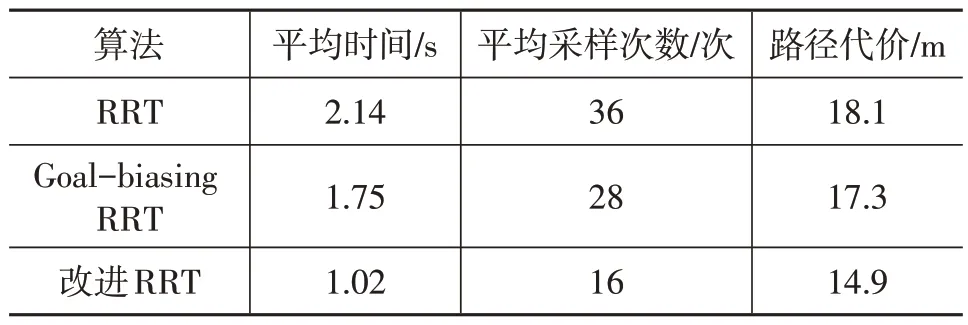
表3 批处理仿真结果
5 结束语
本文对RRT 算法进行了针对性改进,使之更适用于复杂环境下的垂直泊车路径规划。通过融合采样方法减少了采样的随机性及盲目性;通过引入逆向树及RS曲线克服了狭窄通道难以进入的问题;通过RS曲线进行路径优化,平滑了路径并减小了路径代价。
仿真结果表明,本文提出的改进RRT 算法适用于复杂环境下的垂直泊车路径规划,确保了较短的规划时间、较少的采样次数以及相对较短的路径代价,所规划的路径较为平滑,满足车辆约束要求,也尽可能避免了车辆在车位内多余的位姿调整,确保了车辆在复杂环境下泊车过程的安全。

