路径跟踪控制算法仿真分析与试验验证*
赵颖 俞庭 张琪 杨洪涛 宋胜
(西南大学,重庆 400715)
主题词:路径跟踪 预瞄理论 纯跟踪算法 前轮反馈控制算法 模型预测控制算法
1 前言
随着车辆智能驾驶技术的快速进步,底层架构的路径跟踪控制算法不断发展。目前广泛应用的算法主要包括纯跟踪(Pure Pursuit,PP)算法、前轮反馈控制算法、后轴反馈算法和模型预测控制(Model Predictive Control,MPC)算法等。
张龑等人提出了一种基于速度自适应预瞄的无模型控制算法,对于高度复杂的跟踪路径,车辆在低速和高速条件下均具有稳定的跟踪性能。靳欣宇提出了基于前轮反馈控制算法的自适应最优预瞄模型,能够满足车辆在复杂道路上的鲁棒性要求。刘毅等人通过添加PID控制器和低通滤波器使纯跟踪算法得到改善,获得了较好的跟踪效果。Abdelmoniem 等人基于车辆未来状态的离散预测模型,允许在控制器输出增强的未来预测状态时使用前轮反馈控制算法,减小了横向误差,提高了平均偏航稳定性。张涌等人提出基于预瞄控制和模糊滑模控制的车辆横向控制算法,该融合算法使车辆路径跟踪的鲁棒性得到明显提高。王瑞等人提出了基于纯跟踪算法和樽海鞘优化算法的路径跟踪算法,跟踪准确性与车辆运动稳定性得到了提高。Zhang等人基于实时更新系统模型,提出了一种模型预测控制方案,以实现路径跟踪,使车辆在不同驾驶条件下拥有更好的适应性。吴施鹏等人基于二自由度车辆单轨模型,在传统MPC 算法基础上采用遗传算法寻找车辆行驶最优时域参数,减小了车辆跟踪误差,同时加入了前轮侧偏角约束,提升了车辆在低附着系数路面和高速路面上的行驶稳定性。范贤波等人设计了一种基于MPC 的自适应轨迹跟踪控制器,采用模糊控制对预测时域和控制时域进行了在线优化,实现预测时域可根据横向和纵向车速进行自适应选择,提高了轨迹跟踪精度和稳定性。Xu等人基于MPC和预览跟随器理论提出了一种轨迹跟踪方案,计算了预览点处的参考横向加速度以更新状态变量,并在每个预测点生成了参考偏航率,同时将MPC问题转化为线性时变的MPC控制器,构建了连续在线线性化预测模型。
上述文献虽对不同算法在提升车辆路径跟踪精度方面进行了研究,但并未对不同算法在不同工况下的适用性规律进行探究。本文分别构建基于PP 算法、前轮反馈控制算法和MPC算法的车辆模型,采用Simulink和CarSim联合仿真分析的方法,考虑不同道路工况和不同速度工况下3种算法的轨迹跟踪效果,并进行实车试验对比验证3种算法的跟踪性能。
2 理论模型
2.1 车辆转向模型
为了达到理想的传动效果,使车辆在转向过程中各车轮处于纯滚动状态,采用车辆阿克曼转向模型,如图1所示。
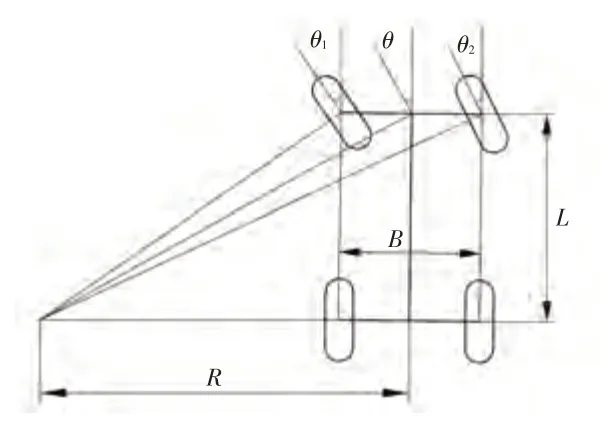
图1 阿克曼转向模型
由图1可得:
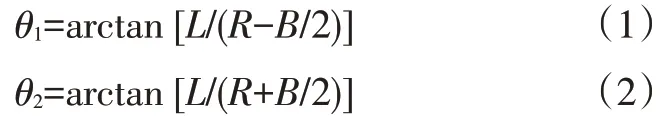
式中,、分别为车辆内、外侧车轮转向角;为车辆轴距;为转向半径;为后轮距。
由几何关系可知,车辆等效转向角为:

2.2 算法理论
2.2.1 基于预瞄的纯跟踪算法
基于预瞄的纯跟踪算法的核心在于基于预瞄路径与当前车辆位置以及转向盘转角之间所建立的几何关系,推导出车辆当前位置与预瞄路径点的关系式,从而得出当前位置的转向盘转角。图2所示为基于预瞄路径的纯跟踪算法模型示意,在阿克曼转向模型的基础上引入预瞄路径,在预瞄路径上取预瞄点,车辆位置参考点为车辆后轴中心点。
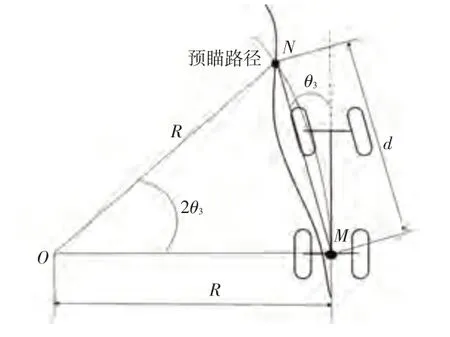
图2 基于预瞄的纯跟踪算法模型
由图2可知,基于车辆位置参考点和预瞄点拟合圆得到转向盘转角,进而控制车辆参考点通过预瞄路径点,最终将车辆约束在参考路径上。
为使车辆参考点顺利通过预瞄路径点,现控制两点位于同一圆上,其中,圆的半径为车辆基于阿克曼转向模型的转向半径,此时前轮转角为,拟合路线半径为,预瞄距离为,由几何关系可得扇形圆心角为2。
根据几何关系可得:

代入式(3)可得车辆转向角为:
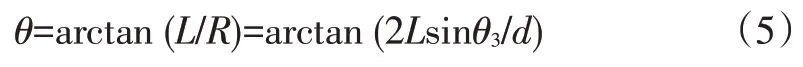
2.2.2 前轮反馈控制算法
前轮反馈控制算法是基于简单车辆运动学模型的直观转向控制律的算法模型,同样使用了阿克曼转向模型,其几何模型如图3所示。
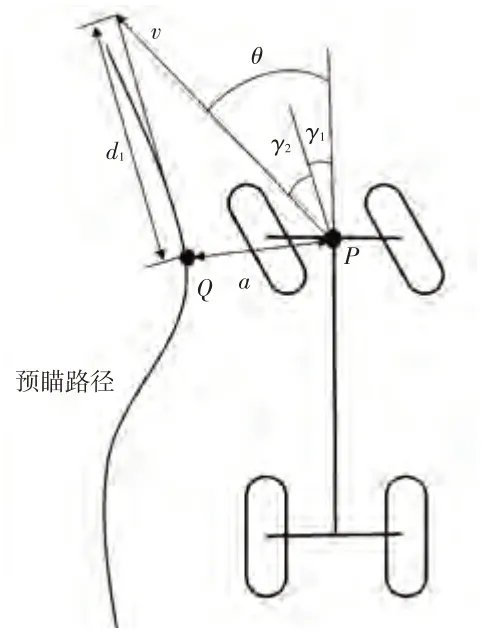
图3 前轮反馈控制算法几何模型
前轮反馈控制算法车辆位置参照点为车辆前轴与车辆纵向中心轴的交点。与基于预瞄的纯跟踪算法不同,该算法采用目标路径上与点距离最近的点为投影点。设、之间的距离偏差为,车速为,车辆中轴线与路径切向夹角为,横向位置偏差补偿转角为,车辆前轮实际转向角为,分别受车辆当前预瞄轨迹中预瞄路径点处的切向角和横向位置偏差补偿转角影响。假设车辆预期轨迹在距离处与给定路径最近点切线相交,其中与速度相关,引入增益代表横向位置偏差在车辆行驶速度下的影响程度,根据几何关系可得:
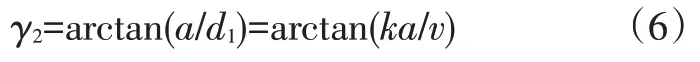
针对式(6),按照误差比例调整横向偏差:当与同时增大时,转向反馈更强烈;较小至收敛至0时,决定了收敛速率。在高速工况下,应选取较大的取值以保证横向误差对于前轮转角的控制效果;在低速工况下,应选取较小的取值以获得稳定的转向反馈效果。
则前轮反馈控制算法的几何关系可表示为:
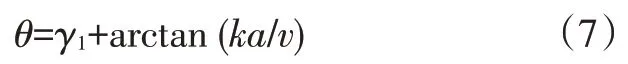
2.2.3 模型预测控制算法
MPC 是一种基于预测模型的闭环优化控制策略。MPC 算法包括预测模型、滚动优化、反馈控制3个部分。
由阿克曼转向模型可知,车辆转弯半径为:

图4 所示为车辆运动模型,其中、为大地坐标系下车辆质心的坐标,为大地坐标系下的车辆航向角,为前轮转角,由图4可知,车辆的状态量为、和。由状态量推导出状态空间为:
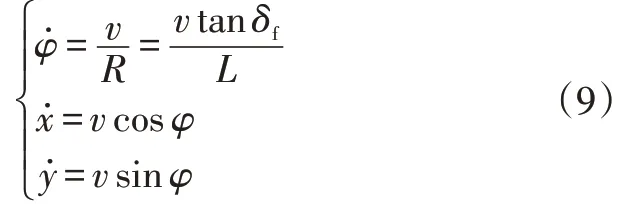
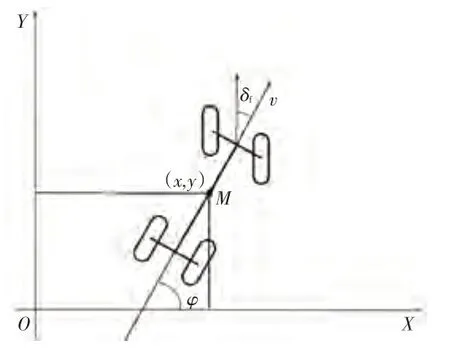
图4 车辆运动模型
显然,上述状态空间呈现非线性,为了采用模型预测控制算法,需要将其处理为线性模型。
线性状态空间关系为:

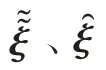
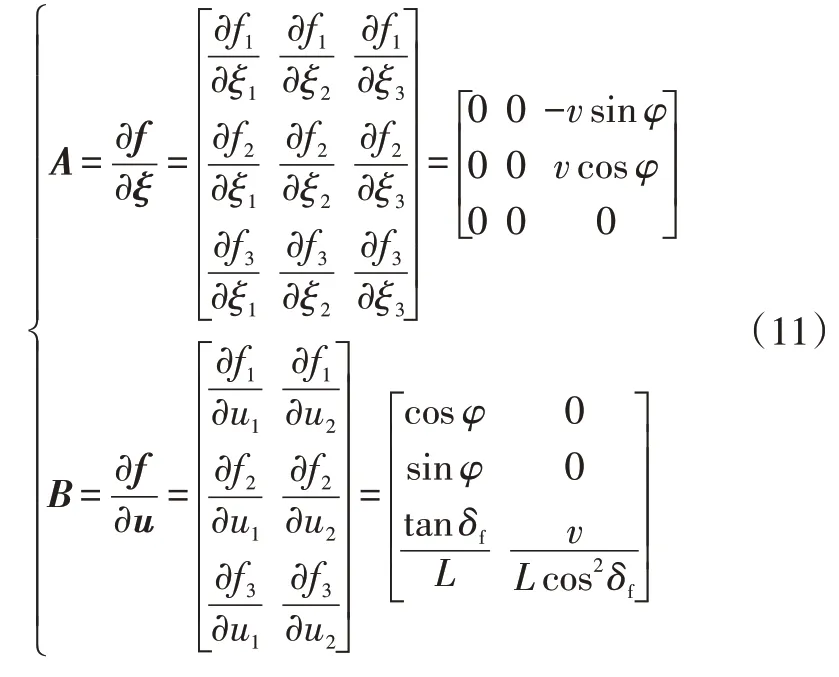
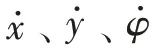
由于处理后的线性模型是连续模型,仍不能用于最终的模型预测控制,还需对其进行离散化。此时:
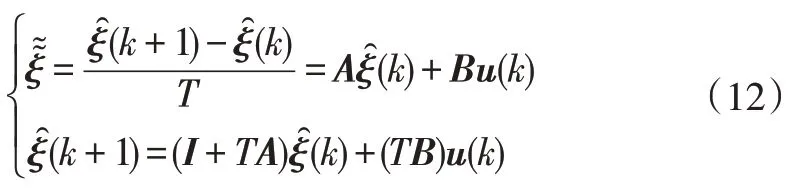
式中,为采样周期。

此时,用于预测控制的离散模型构建完成,得到线性时变的状态空间:
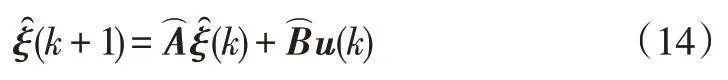
目标函数形式为:
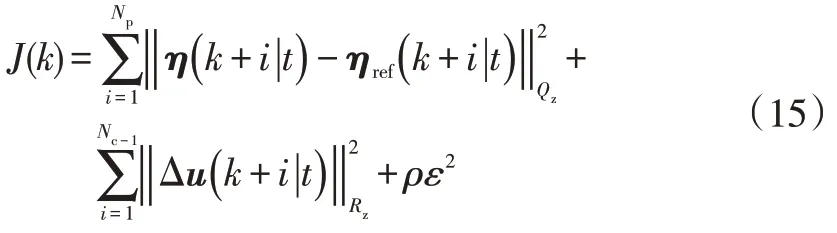

目标函数用来计算未来一段时间系统的输出值,基于线性误差模型预测车辆未来时刻输出的目标函数。
将式(15)简化为:

状态空间采样矩阵;=[Δ() Δ(+1) Δ(+2) …Δ(+-1)]为控制量偏差变化量采样矩阵。
优化模型的目标是使当前状态尽快收敛到参考值,即尽可能收敛到,同时输入量的改变量尽可能小,即趋向于0。为量化各参数对控制性能的影响程度,通过求加权平方和的方式来体现:

式中,为半正定状态加权矩阵;为正定的控制加权矩阵。
控制的目的是使式(17)的值尽可能小。但式(17)并不是二次规划问题,其涉及的控制量过多,而在实际控制中,控制量为输入。定义偏差为:

计算整理后有:
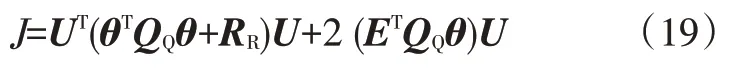
式(19)可写为:

式中,=+;=。
则式(17)可改写为:
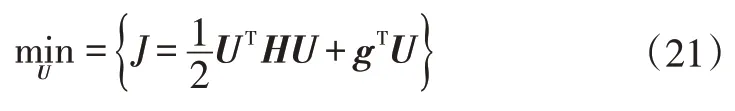
此时,目标函数转为标准二次规划问题,将优化目标函数的问题表示为以为变量求解该二次规划使得目标函数最小的问题。式(21)的约束条件为≤≤,、分别为控制量的下界和上界。通过解决二次规划问题,可求解控制量,并在中提取第1 项输入量(),将其输出至控制车辆以实现对车辆的模型预测控制。
3 仿真分析
3.1 基于预瞄的纯跟踪算法
由前文可知,基于预瞄的纯跟踪算法的预瞄距离是影响横向误差的主要因素之一,因此,针对纯跟踪算法,车速分别选取5 km/h、50 km/h、80 km/h、120 km/h,在低、中、高速工况下改变预瞄距离进行探究。仿真圆环道路模型和蛇行道路模型如图5所示。共设计5组预瞄距离,最小预瞄距离应大于车辆最小转弯半径,普通车辆最小转弯半径约为5 m,预瞄距离增加至15 m且车速120 km/h 时横向误差将超过1 m,跟踪效果较差。因此,选取预瞄距离分别为5 m、8 m、10 m、12 m、15 m。仿真结果分别如图6、图7所示。
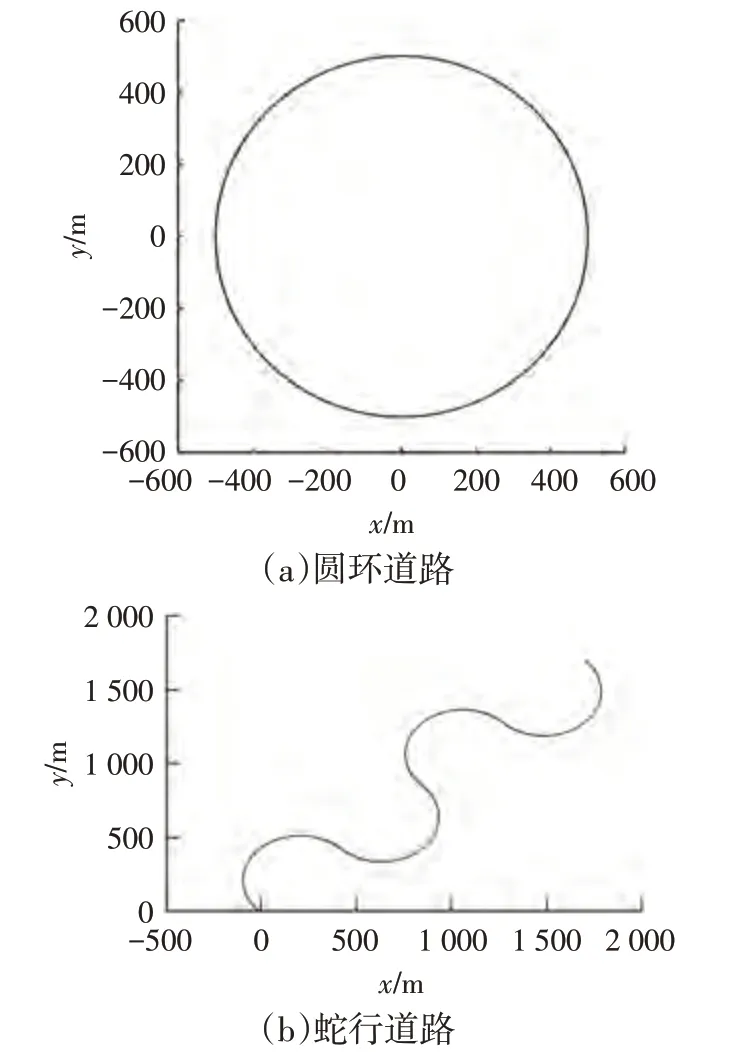
图5 仿真道路模型
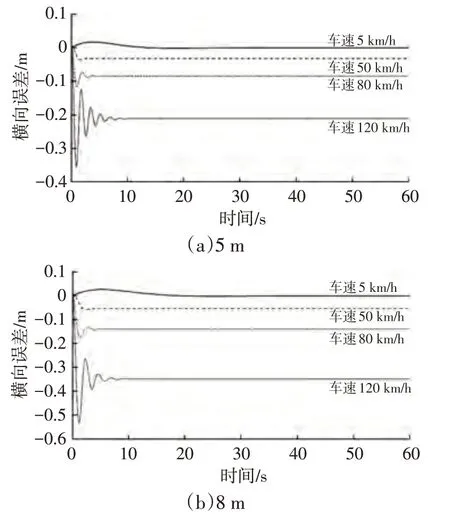
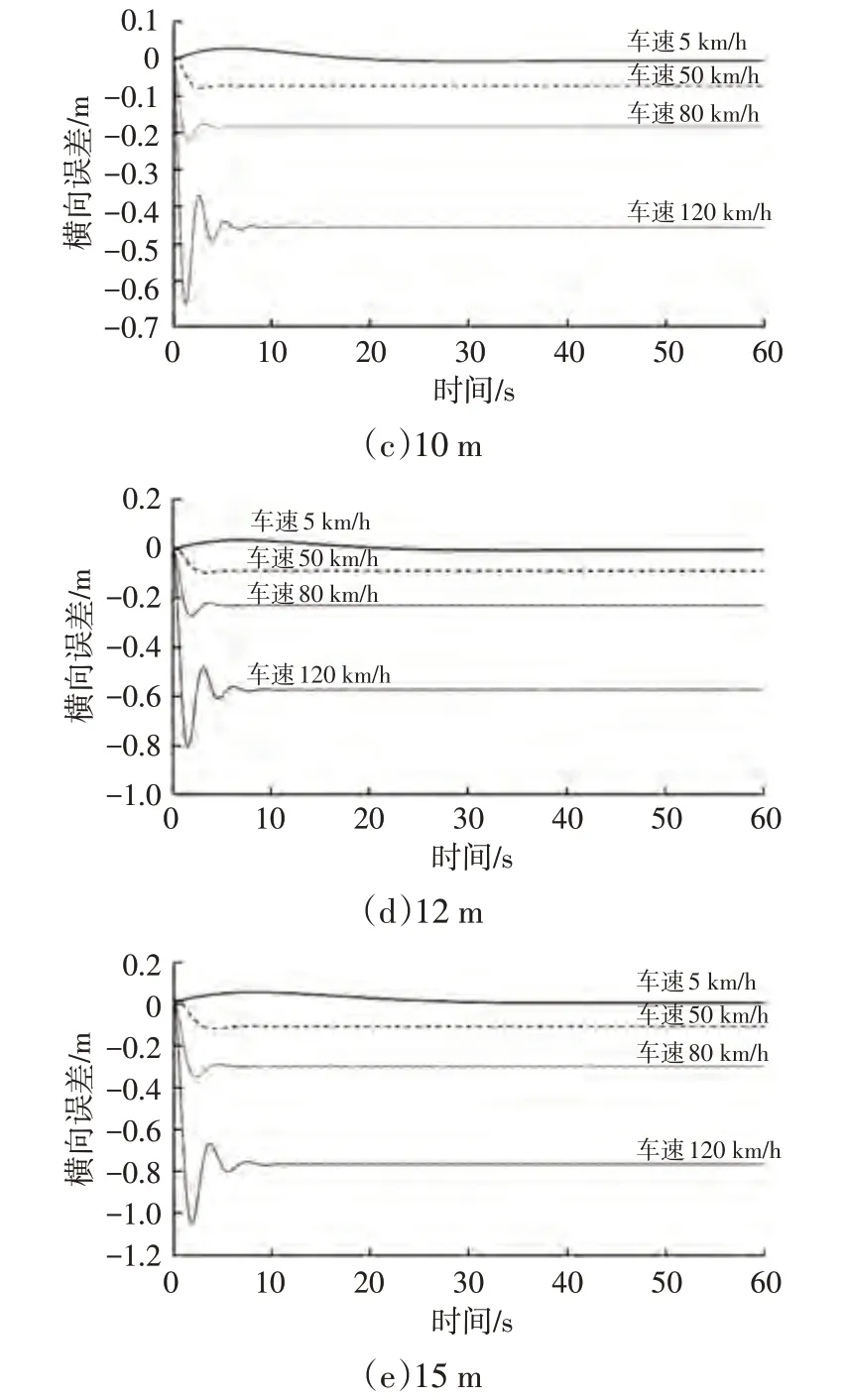
图6 圆环道路不同预瞄距离下纯跟踪算法的横向误差
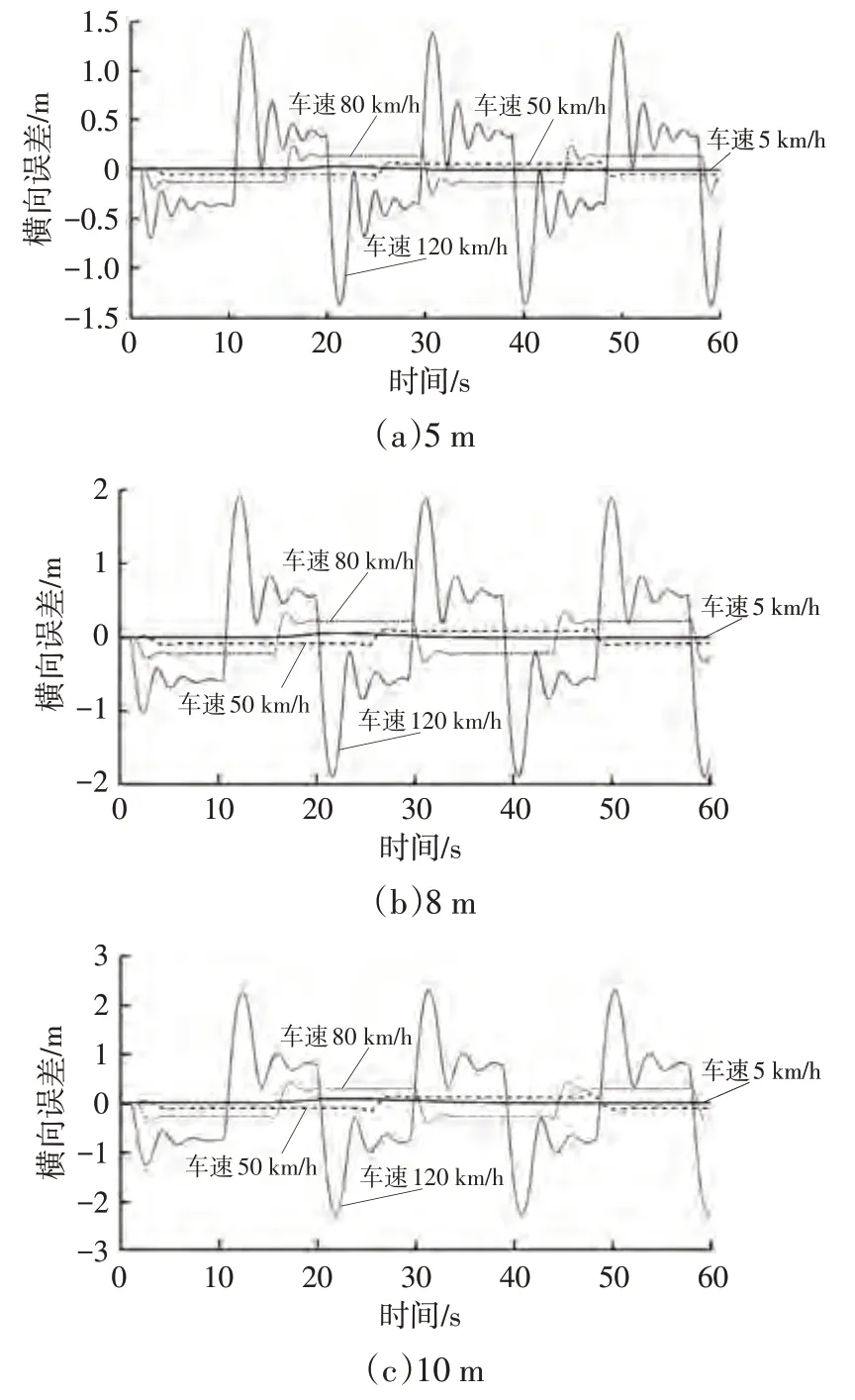
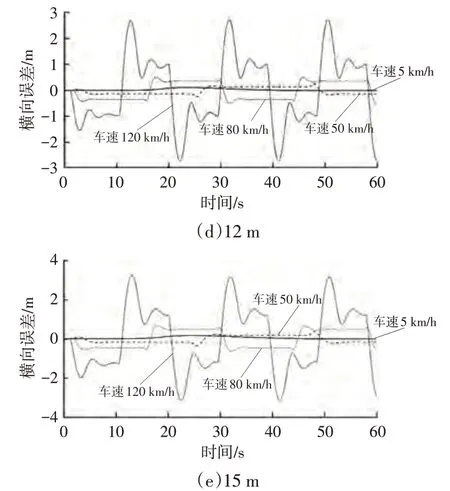
图7 蛇行道路不同预瞄距离下纯跟踪算法的横向误差
由图6、图7 可知,圆环道路工况下,车辆行驶时横向误差逐渐收敛于确定的值。基于预瞄的纯跟踪算法中车辆基于预瞄点的横向误差影响的大小,进而影响车辆转向角。圆环道路曲率固定为0.002 m,算法为控制车辆在参考轨迹上稳定行驶,使车辆的横向误差逐渐收敛于确定的值。蛇行道路工况下,道路曲率规律性变化,横向误差也随之规律性变化,80 km/h 和120 km/h 工况下,随着预瞄距离的增大,横向误差的振荡不断减小,车辆跟踪稳定性提升。预瞄距离越短,最终收敛的横向误差越小,即算法跟踪的精度越高,但收敛变慢,随预瞄距离的增加,收敛横向误差逐渐增大,误差收敛时间逐渐缩短,即算法的稳定性提高。增大预瞄距离可使算法获得更强的稳定性,但预瞄距离过大会使横向误差和误差收敛时间变大,跟踪效果变差。
基于此,横向误差可以通过缩短预瞄距离的方式加以限制,部分文献中选取预瞄距离为:

式中,=1/(2);为车辆最大制动加速度;为最短制动距离;为车辆遇到异常时需要的反应时间;为车辆的最小转弯半径。
3.2 前轮反馈控制算法
增益系数是影响前轮反馈控制算法控制性能的重要因素之一。因此,选取不同增益系数的取值(0.1、0.5、1.0、2.0、5.0、10.0、15.0、35.0、50.0),在低、中、高速(5 km/h、50 km/h、80 km/h、120 km/h)工况下,进行圆环及蛇行道路仿真分析,仿真结果分别如图8~图10所示。
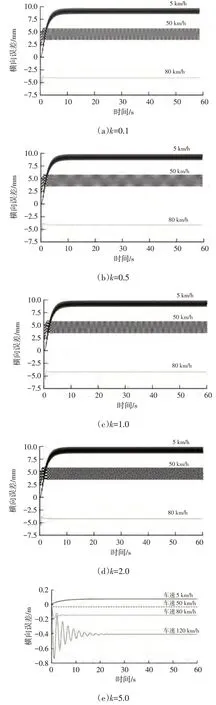
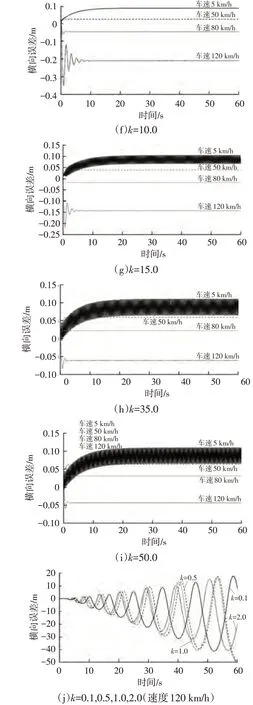
图8 圆环道路不同增益系数下前轮反馈控制算法横向误差
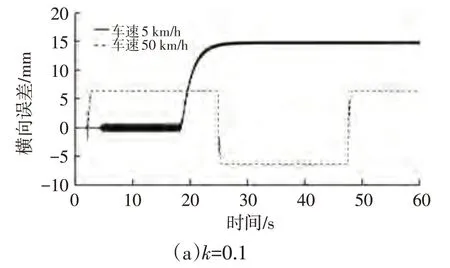
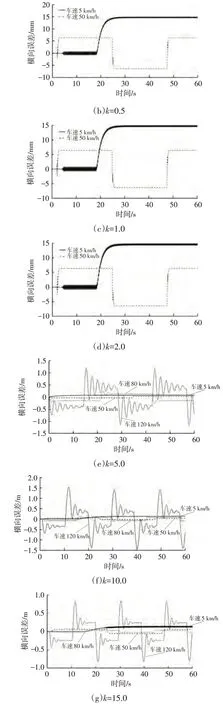
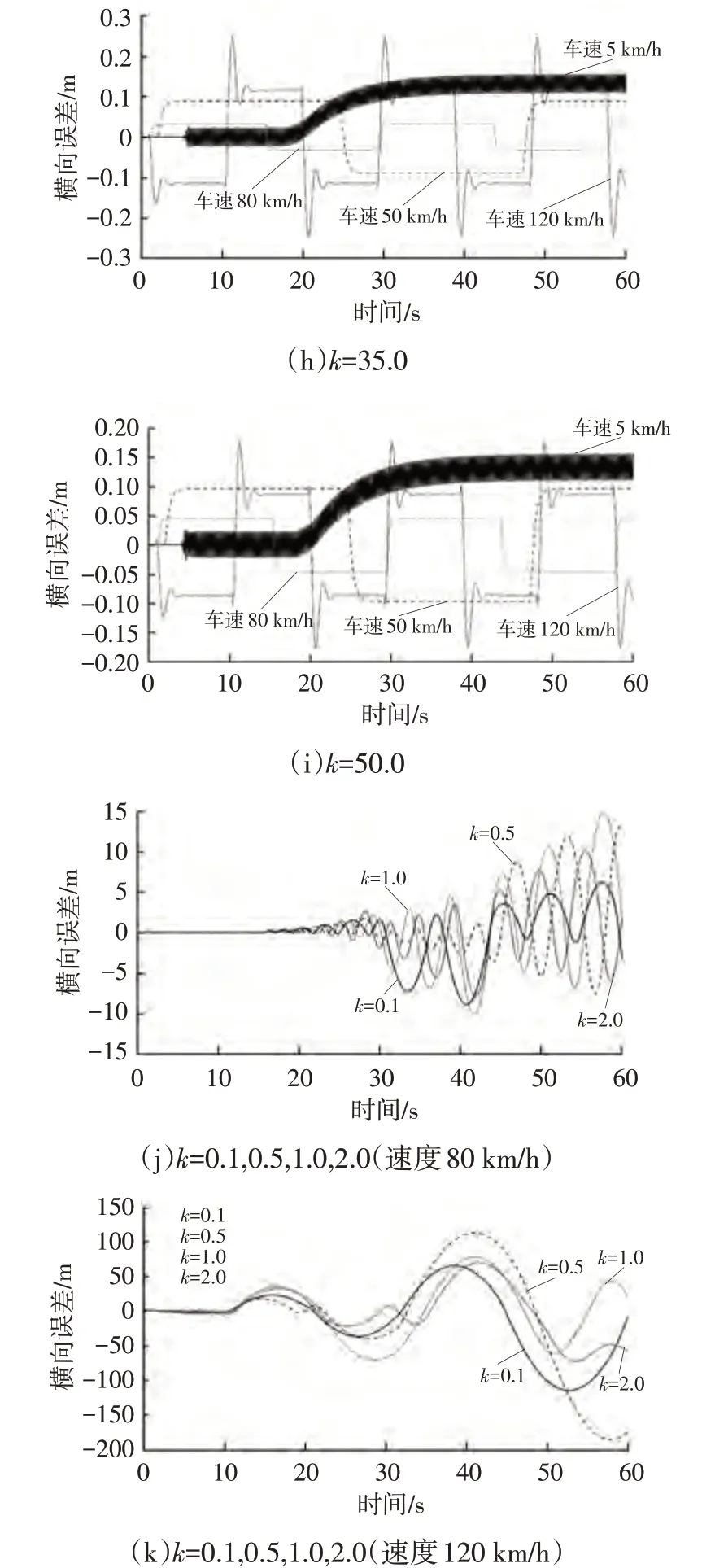
图9 蛇行道路不同增益系数下前轮反馈控制算法横向误差
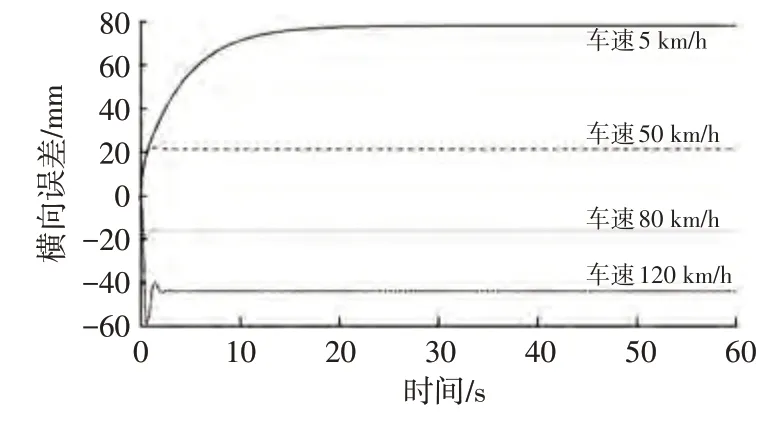
图10 圆环道路k=Dv+E下前轮反馈控制算法的横向误差
由图8~图10可知,在所选的不同车速工况条件下,值的选取对前轮反馈控制算法横向控制的性能皆有显著影响。在同一增益系数、不同速度工况条件下,横向误差均收敛于一定的误差范围内。5 km/h 车速工况条件下,仿真车辆横向误差曲线出现振荡,且振幅随着增益系数的增加而增加。其原因是此时式(7)中与速度的比值较大,进而横向误差对车辆转角的影响较大。同理,=0.1,0.5,1.0,2.0 时,圆环道路120 km/h 车速、蛇行道路80 km/h、120 km/h车速工况下,横向误差不断累积增大,无法收敛,原因在于较小的增益系数会降低横向误差对车辆转角的影响,使横向误差无法收敛。同一速度下,增益系数与横向误差并非简单的线性关系。4种速度下,算法可找出与速度相关的最优增益系数(由于<5时高速工况下横向误差无法收敛,仅考虑≥5的5组),可进一步探寻最优增益系数以获得最小误差。基于此,为使前轮反馈控制算法具有更佳的控制性能,可使增益与车辆速度呈现一定的函数关系,使算法在不同速度工况下得出最佳的增益。对此,进行进一步仿真探究,根据上述4组不同速度工况下相对应的最佳增益系数,提出增益与速度的一次函数拟合关系:

式中,、为可调节的常数。
由仿真数据进行拟合得到不同速度下达到最小横向误差时增益系数的取值。进一步,通过一次项直线拟合得出=0.388、=4.125时,在不同速度工况下可得到最小横向误差。该一次函数拟合关系下,4种速度下的横向误差分别为0.065 47 m、0.020 43 m、0.015 34 m、0.055 69 m,均低于对应速度下增益系数=5,10,15,35,50时的横向误差。因此,通过本文所提出的增益与速度的一次函数拟合关系,可计算出对应速度下的增益,使算法达到更好的控制效果。
3.3 MPC算法
MPC 算法在5 km/h、50 km/h、80 km/h、120 km/h 车速工况下,圆环及蛇行路径下的仿真结果分别如图11、图12所示。
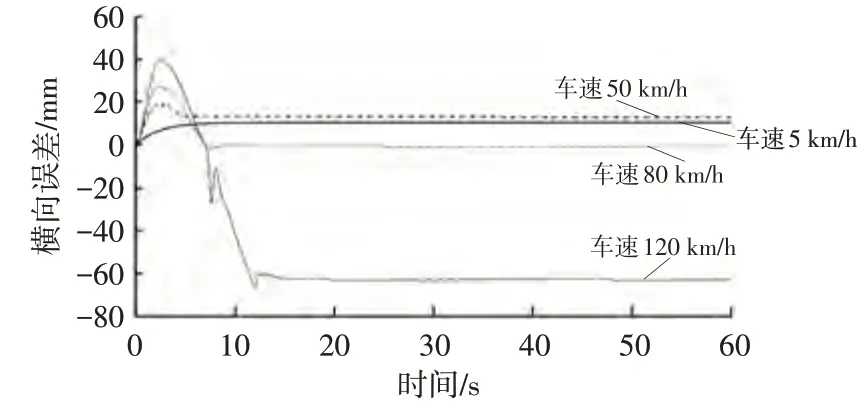
图11 圆环道路下MPC算法的横向误差
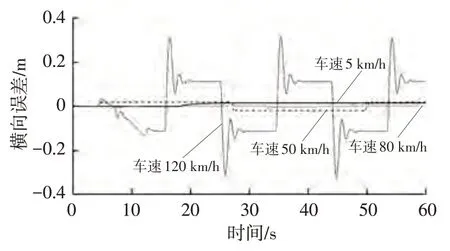
图12 蛇行道路下MPC算法的横向误差
由图11、图12可知,MPC算法表现出优异的跟踪效果,4种速度下的横向误差均维持在一定范围内。相较于纯跟踪及前轮反馈控制算法,MPC算法在各速度工况下皆具有更优的控制性能,横向误差更小,蛇行弯道下横向误差的波动更小,具有更好的鲁棒性。在5 km/h的低速工况下,MPC算法横向误差小于性能较好的纯跟踪算法横向误差。在120 km/h的高速工况下,MPC算法横向误差小于高速情况下性能较好的前轮反馈控制算法横向误差。其原因是,MPC算法具有良好的横、纵向耦合控制性能,能够对仿真车辆的速度进行控制,使得算法具有良好的预测作用。当车辆需在弯道转向时,MPC算法能够在车辆到达弯道转向前进行减速控制,使车辆在弯道转向时不至于失稳,转向过程更加平滑。
综上,相较于纯跟踪及前轮反馈控制算法,MPC 算法具有更好的路径跟踪控制性能。在高速及低速工况下,横向误差更小,算法的鲁棒性更好,适宜各速度工况。
4 实车试验
4.1 试验平台与场地
本文选用搭载高精度全球卫星导航系统(Global Navigation Satellite System,GNSS)/惯性导航系统(Inertial Navigation System,INS)的无人驾驶平台进行试验,该平台如图13 所示。试验场地为某400 m 运动场圆弧跑道,试验运动场局部如图14 所示。受试验条件制约,在5 km/h速度工况下进行算法路径跟踪试验。

图13 无人驾驶平台

图14 试验运动场局部示意
4.2 实车试验结果
由于GNSS/INS 组合导航系统可提供连续、可靠和完备的高精度导航参数,选用GNSS/INS 组合导航获取的定位数据作为车身位置。试验结果如图15所示。
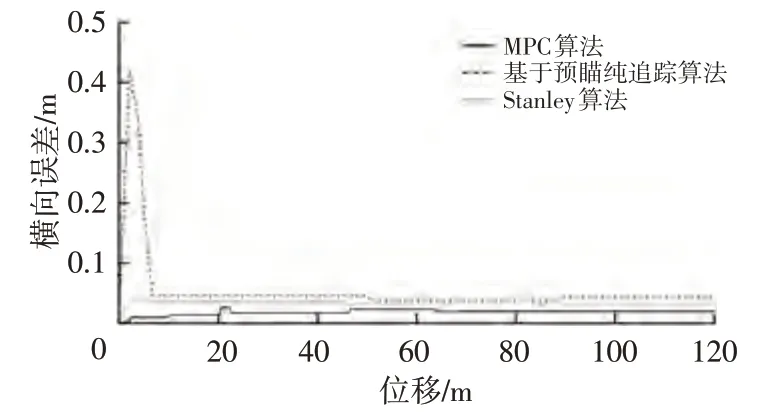
图15 跟踪算法试验横向误差曲线
由图15可知,MPC算法具有更小的横向误差、更好的跟踪性能。以纯跟踪算法横向误差为基准,MPC算法实车试验中的横向误差较小,横向最大误差仅0.02 m左右,这是由于MPC 算法能够对车辆的横向偏差进行预测,使得车辆跟踪误差能够迅速减小的同时避免控制的发散,算法能发挥更优良的预测作用。由此实车试验验证了该工况下MPC算法具有更好的路径跟踪控制性能。
5 结束语
本文对基于预瞄的纯跟踪算法、前轮反馈控制算法、MPC 算法3 种控制算法进行CarSim-Simulink 联合仿真分析,并通过试验进行仿真结果验证。分析结果显示:基于预瞄的纯跟踪算法在车辆低速工况下的路径跟踪鲁棒性较好,高速横向误差较大,预瞄距离是影响其跟踪性能的主要因素之一;相较于基于预瞄的纯跟踪算法,前轮反馈控制算法在高速工况下的路径跟踪效果具有更好的鲁棒性;MPC 算法具有更好的横向控制性能,在高速和低速工况下皆具有更优的预测效果。
本文仅对道路车辆的路径跟踪横向控制进行了研究,后续将针对崎岖、颠簸等复杂道路工况下,综合考虑横、纵向等多方向,对车辆的多向控制进行研究,进一步提升车辆路径跟踪效果的同时增强鲁棒性。所研究的3种算法在不同工况下可表现出差异化的跟踪性能,在实际运行过程中,车辆面对不同道路状况的变化、车速限制等,可通过车载传感器反馈车辆的真实状态,以精确判断工况,从而实现算法的自适应选择,这将是后续研究的重点。

