矿用带式输送机关键部件悬垂度分析与数值模拟*

邵鹏峰

(潞安化工集团司马煤业有限公司，山西 长治 046000)

0 引 言

带式输送机是散料输送领域最常用的一种机械设备，目前比较广泛应用在煤矿、选煤厂、铁矿和非金属矿等矿山领域[1]。通用带式输送机主要由机架部分、输送带部分、一系列托辊和驱动电机等部分组成，其中输送带是带式输送机最重要的部件之一，由于输送带在实际运行过程中，不仅受到托辊的支撑力，同时还受到物料的压力和摩擦力，受到物料的冲击、在启停过程中会产生比较大的动态张力、同时还会受到弯曲应力的作用，为此要求输送带具有足够大的强度和抗冲击的性能[2]。

带式输送机在运行过程中会因受到物料不均匀载荷的影响，出现悬垂度过大、内部张力过大的问题，输送带运行不平稳，将会导致物料的洒落或托辊的受力不均匀，有可能引起断带事故，造成人员伤亡。为此研究输送带悬垂度问题，掌握输送带悬垂度变化规律，分析不同托辊间距下输送带的悬垂度规律，可以指导最小张力的求解，从而有利于保证带式输送机的平稳运行，避免发生断带事故。

笔者通过对带式输送机输送带基本特性的分析可知，输送带的粘弹性特性会引起输送带的挠度变形从而会影响输送带的悬垂度，由此建立了输送带的粘弹性数学模型，采用有限元法进行了模拟仿真分析，研究了影响输送带悬垂度的因素和受载时的悬垂度变化规律。经过验证可以指导带式输送机最小张力的求解以及延长输送带的使用寿命，对提高带式输送机的安全运行系数具有重要的参考意义。

1 带式输送机关键部件特性分析

输送带主要由内部的钢丝绳和外部覆包的高弹性橡胶组成，结构刚度比较低，主要特性表现如下[2]。

(1) 应力-应变非线性特性 输送带属于挠性体，在承受拉力作用的时候，拉力的大小和变形的大小本身并没有呈现出线性关系，最终表现为非常明显的非线性特性，输送带将一部分的能量通过弹性变形吸收，另一部分能量转化为内能。

(2) 蠕变和松弛特性 输送带在定载荷施加时，输送带的最终伸长量会随着时间逐渐增加，当经过一段时间后，输送带的伸长状态稳定，但其本身存在一定的塑性变形，会导致最终的长度不可逆。

(3) 频响和滞后特性 输送带的实际变形量与加载过程的载荷变化频率相关，当加载的载荷频率增大时，输送带的振动特性将会发生变化。在一个加载周期内，输送带的应变需要一段时间才能够恢复到初始状态。

2 输送带粘弹性数学模型分析

输送带是具有纵向加强材料的高聚合物材料，输送带纵向力学特性具有粘弹特性，在实际受载荷作用时，输送带会产生蠕变特性，在纵向方向会产生弹性变形，导致输送带的悬垂度变大，影响输送带输送的平稳性。为了分析输送带的悬垂度问题，需要建立输送带的粘弹性数学模型，研究输送带的应力和应变的非线性特性，分析输送带在受到载荷作用时输送带的理论数值变形情况，然后再对输送带变形进行数值模拟验证。为了分析输送带的悬垂度与自身特性的规律，采用数学模型进行推导和计算机模拟仿真的方式进行研究。

2.1 输送带粘弹性数学模型建立

实际应用表明，输送带的粘性和弹性仅是反应输送带材料特性的一方面，实际的理想弹性模型和理想的粘性模型最终是反映这两种性质最理想的模型[3]。最终的表达式为：

σ=Eε

(1)

式中：σ为应力；ε为应变；E为弹性模量。

理想的粘性模型也就是所谓的牛顿粘滞体模型，相当于是一个储能元件，在电路系统中可以当做是一个阻尼，按照阻尼的基本规律，速度和阻力呈现出负相关，反映出的是粘性介质中某个点的应力和应变的关系，表示为：

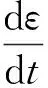
(2)

式中:ϑ为粘滞系数。需要以实际使用的输送带模型作为分析模型，为此此次分析搭建Maxwell模型。从上式中可以看出输送带的应力与应变之间存在非线性特性。

2.2 带式输送机参数特征与设定

带式输送机是重要的物料输送设备，为保证仿真结果的一致性和可靠度，采用实际应用中的带式输送机参数作为仿真模型，表1所列为带式输送机参数特征。

表1 带式输送机参数特征

根据以上提供的输送带的相关参数，采用经典的悬链线方法和弹性悬链线方法分别进行计算，得到计算结果：①经典悬链线方法[4]：辊间输送带的最大垂度0.013 4 m，则其相对垂度为0.008 9，符合《DTII(A)型带式输送机设计手册》规定的最大垂度要求；②弹性悬链线方法：由式(2)可得弹性悬链线辊间输送带最大垂度为0.053 5 m，相对垂度为0.035 7，略大于《DTII(A)型带式输送机设计手册》中给定的数值。

3 基于ANSYS的输送带悬垂度仿真结果

由于目前国内对输送带悬垂度分析较少，文中在ANSYS软件中建立输送带模型，并且按照表1所列的参数对输送带进行设置，可以得到如图1所示的仿真结果。

图1 输送带悬垂度位移仿真结果

由图1中看出，输送带最大悬垂度为0.057 864 m，在两个托辊最中间位置悬垂度最大，两个托辊的距离为1.5 m，仿真分析的结果与实际采用悬链线方程进行求解得到的结果0.053 5 m吻合，由此可以得出采用传统的悬链线理论求解输送带的悬垂度最终存在一定误差。为了分析输送带实际运行张力与托辊间距对输送带的悬垂度的影响，分别进行设置不同的托辊间距对输送带进行仿真分析，可以得到如图2所示的分析结果。

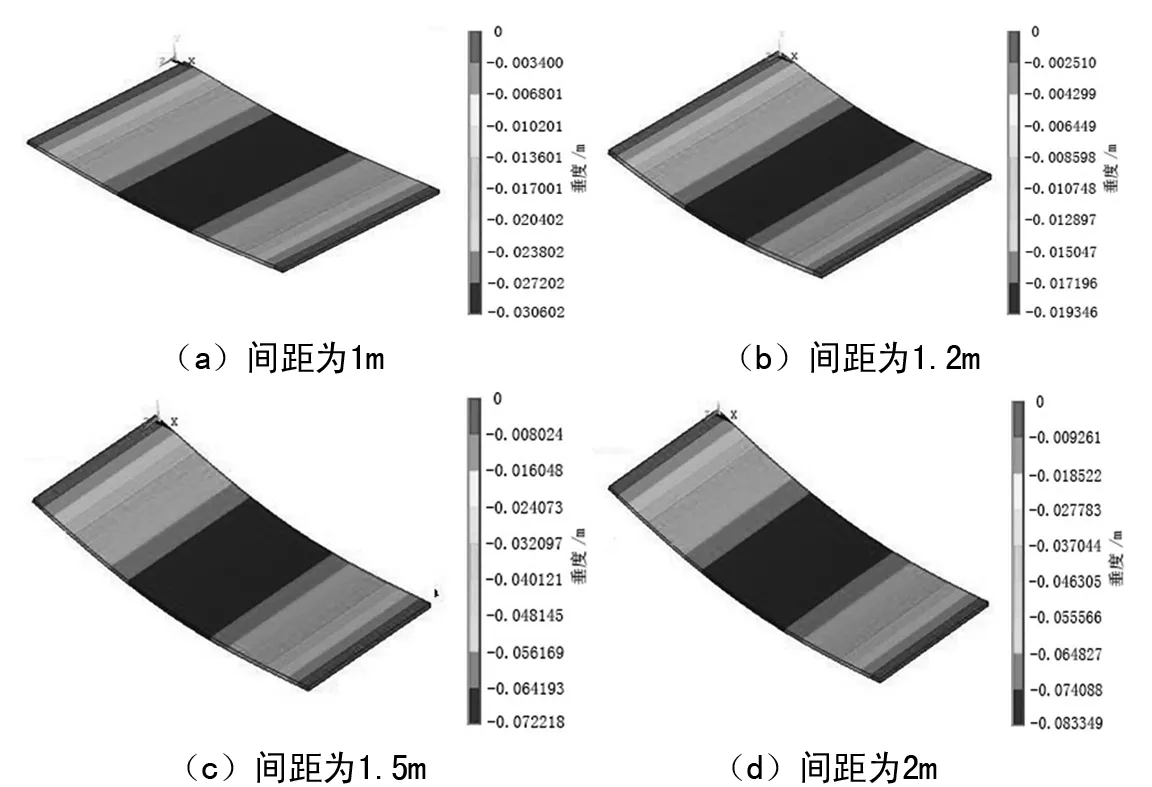
图2 不同托辊间距下输送带的悬垂度仿真结果

输送带张力设定为14 200 N，通过设置不同的托辊间距，分别为1 m，1.2 m，1.5 m，2.0 m间距作为对照，对输送带进行仿真分析，可以得到四组仿真结果，从上述的仿真结果可以看出，在不同的托辊间距下输送带的中间悬垂度有所不同，其中间距越大表现为悬垂度越大。

为了分析不同的张力情况下输送带的悬垂度情况，设定不同的张力值，分别为15 630 N，18 470 N、21 300 N，24 000 N，可以得到如图3所示的仿真分析结果。

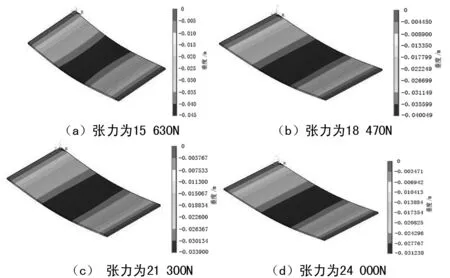
图3 不同张力作用下输送带悬垂度仿真分析结果

由上述分析结果可看出输送带在不同张力作用下，输送带悬垂度分布云图呈现出一定的规律性，悬垂度最大的位置仍然集中在中间部位，当张力变大时悬垂度中间区域变大，为了更清晰地展示悬垂度的变化，将上述的分析结果绘制曲线进行分析。

4 仿真结果对比分析

将ANSYS仿真结果导出，分别以托辊间距和张力值为横坐标，以输送带的悬垂度作为纵坐标绘制曲线，可以得到如图4所示的对比分析结果。图4(a)所示为输送带最大悬垂度随托辊间距的变化曲线，图4(b)输送带最大悬垂度随输送带张力的变化曲线。

从图4(a)中可知，当输送带的托辊间距分别取1 m，1.2 m，1.5 m，2.0 m时，输送带对应的最大悬垂度为0.019 m、0.031 m、0.072 m、0.083 m，可以得出在输送带恒定张力作用下，托辊的间距越大，辊间输送带的最大悬垂度将会急剧增加，变化幅度较大，所以需要保证托辊在合适的范围之内，有效避免输送带悬垂度过大。从图4(b)中可以得出当设定不同的输送带张力时，输送带的最大悬垂度分别为0.045 m、0.040 m、0.034 m、0.031 m，从曲线中可以得出输送带在相同的托辊间距情况下，当输送带的张力增加时，托辊输送带最大的悬垂度在逐渐减小，但是两者之间并不存在某种线性关系。

图4 输送带最大悬垂度计算值与仿真结果对比

从上述的分析结果可以看出，基于弹性悬链线方程的不同托辊间距的输送带最大悬垂度计算的结果与仿真结果一致，验证了理论分析的正确性。

5 结 语

针对矿用带式输送机随托辊间距和张力变化规律未知等问题，文中建立了带式输送机输送带粘弹性动力学模型，并利用ANSYS对输送带进行有限元分析，最终得出输送带的最大悬垂度随着托辊间距的增大而增大，随输送带自身张力的增大而减小，此研究规律可以为输送带最小张力的求解提供参考，同时对于带式输送机则需要通过合理布置托辊间距、保证合适的张力值，从而可以减小输送带的悬垂，保证物料的输送。