基于AP-FBSOMP组合算法的轴承微弱故障智能诊断分析

于春霞，张建国，李 明

（1.黄河科技学院计算机系，河南郑州 450063；2.河南理工大学机械工程学院，河南郑州 451460；3.河南力天刀具有限公司技术开发部，河南郑州 450053）

压缩感知（CS）属于一种获得广泛研究的理论方法，能够大幅提升信号分析效率，对于简化计算过程以及提升模型预测准确性具有关键作用，此外也可以将其应用于无法通过奈奎斯特方法进行采样制约的领域［1-2］。对于信号的数据采集与压缩过程进行压缩感知处理时，只需设置合适数量的采样点便可以重构信号特征，由此减少采样点个数并在更小空间内完成数据压缩存储［3-4］。因此，压缩感知处理技术已成为现阶段开展数据采集、仿真信号分析、图像数据处理、高速通信等众多领域的重点研究课题。

根据压缩感知理论存储压缩处理数据时，需对各项信号进行重构，因此需先存储稀疏矩阵与测试矩阵，同时发现扩大信号规模后，形成了更大的存储空间［5］。为了确保可以在更小空间范围内完成矩阵的存储过程，国内学者严保康等［6］设置了分块压缩的方法处理语音信号，完成信号的快速感知计算。杨淑媛等［7］构建了仿真模型来实现图像纹理数据的自动分析功能，从而完成快速分块压缩感知。通过上述分块压缩感知处理后，大幅降低了稀疏矩阵数据存储空间。采用连续监测方法分析机械设备运行过程的故障情况时，需要提供很大存储空间才能满足要求，为减少数据空间的占用量，可以采用语音信号分帧处理或对图像数据进行分块的方式进行电机轴承故障数据的压缩，能够显著控制故障数据存储过程所占的空间。对初始采集获得的压缩信号进行重构后，再对故障信号种类实施重构［8-9］。根据常规经验值进行分块时无法实现机械振动信号的高效处理，从而导致重构精度受到较大影响［10］。

利用重构算法处理时应根据信号稀疏度参数确定合适的支撑集，但进行实际应用时并不能有效预测信号稀疏度。Donoho等［11］通过预先设定判断阈值的方式建立了分段正交形式的匹配追踪算法（SOMP），由此达到重构支撑集原子的效果，可以针对未知稀疏度情况实施重构计算。张淑清等［12］则对图像进行SOMP计算后发现该算法大幅缩短了图像重构时间。为了实现电机轴承故障信号快速完成分块压缩感知功能，构建了自适应分块的方法对分段正交过程进行匹配追踪。由于上述处理方法中包含了信号分块与K奇异值分解（KSVD）的过程，有助于在保持稳定信号块稀疏度状态下减小信号块稀疏度，之后进一步优化了SOMP算法，在重构阶段对支撑集二次筛选后形成排列结构更加合理的支撑集原子组成方式，由此大幅改善了重构性能。

1 AP-FBSOMP重构算法

1.1 自适应分块方法

为了将信号重构状态调整到最佳状态，可以利用自适应分块（AP）的模式来实现，同时根据信号特征设置合适的分块长度，显著改善信号块稀疏度的均衡性［13］。

轴承故障信号分解成分示意图如图1 所示。图1 中，对电机轴承进行运行故障检测发现共存在3 种信号类型，分别为冲击信号、固有信号、噪声信号，此外还可以将其理解为是通过冲击成分与固有成分进行复合的信号再跟噪声信号混合后的结果［14］。

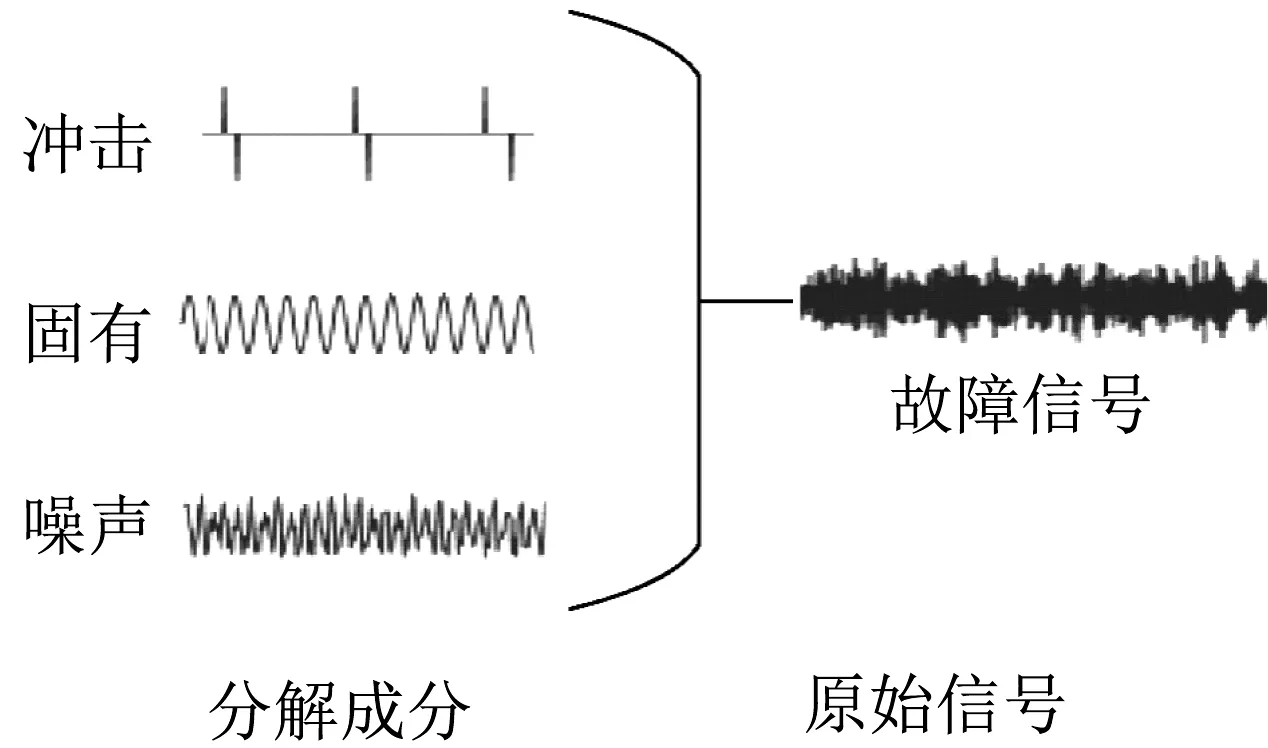
图1 轴承故障信号分解成分Fig.1 Decomposition component of bearing fault signal

以下给出了信号计算的表达式为

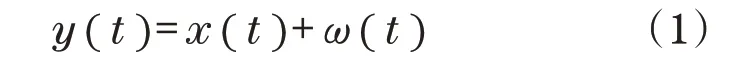
式中：y（t）为轴承的故障信号；ω（t）为噪声信号；x（t）为是不同复合信号。

以下表示电机轴承出现故障问题时构建的x（t）模型［15］：

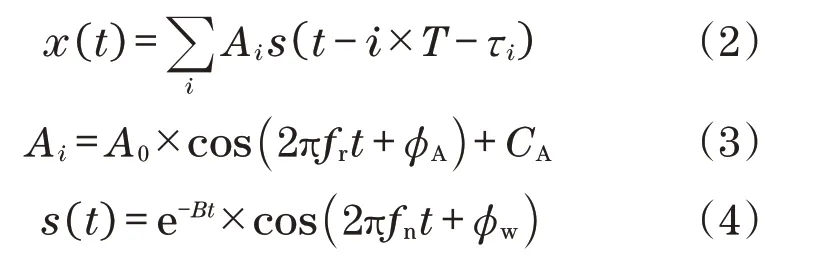
式中：Τ为第i次冲击造成的波动幅度；s（t）为冲击阶段形成的衰减振荡；fn为轴承运行时的固有频率；fr为旋转频率；CA为常数；B为衰减系数；A0为在激励条件下的共振强度；ϕA与ϕω均为初始相位。

Ai和s（t）2 个信号都呈现周期变化的规律，由以上信号构成的复合信号x（t）也形成了具有周期性变化的结果。按照x（t）信号的周期完成信号的分块过程，保证不同分块中都产生同样冲击信号和固有信号，完成稀疏转换后，信号获得了一致稀疏度，此时每个分块都形成了均衡稀疏度。

受噪声信号影响后，不能准确判断复合信号x（t）每个周期的长度。通过分析故障信号特点从语音信号提取得到基础周期数据，再以短时自相关方式获得复合信号周期，在此基础上自适应设置信号的分块长度，显著提升分块稀疏度的分布均匀性，由此重构得到高精度的信号。

按照以下表达式定义故障信号Yn（t）自相关函数Rn（τ）：

式中：L为y（t）窗口长度；Yn（t）为故障信号。

1.2 算法重构支撑集分析

为提高SOMP 算法在较大稀疏度下进行重构的效果，由此实现重构支撑集的优化功能［15］：

假设重构支撑集是由E1、I1共同组成。对信号进行重构时，支撑集由E集合原子构成，进行支撑集原子选择时属于对E集合有效支撑集原子进行确定的过程。

1.3 算法流程

本文采用自适应分块的方式对前后向各段进行正交匹配追踪，算法流程如图2所示。

图2 算法流程Fig.2 Algorithm flow chart

2 仿真分析

2.1 支撑集仿真分析

利用以下式子进行振动仿真信号的测试：

以上信号是利用各频率正弦信号叠加形成的，设定频率为5 000 Hz 的条件实施采样，测试形成图3中的时域波形。

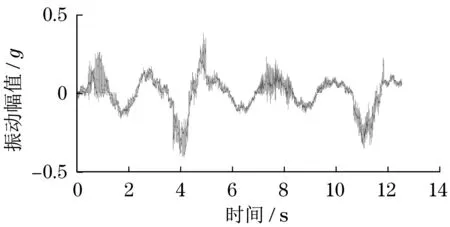
图3 仿真信号波形Fig.3 Simulation signal waveform

本次测试的高斯数据长度256，稀疏度为30，由此得到SOMP 算法重构支撑集，再对100×256 高斯随机矩阵进行测试。

本实验设置了多种类型的有效支撑集并开展重构测试，之后逐渐增加重构支撑集原子数。为对比各个支撑集对重构性能产生的作用，将有效支撑集的原子数设定在1～30 之间，同时设定步长为5的情况再将支撑集原子数从0 逐渐升高至40，从而得到不同条件下的重构误差，测试结果见表1。

表1 相对误差随支撑集原子数变化Tab.1 Relative error changes with atomic number of support set

从表1 中可以看到，随着重构支撑集的有效支撑集原子数增加后，获得了跟初始信号误差更低的重构信号，可以推断两种信号形成了更相近状态。重构支撑集中的原子数对测试误差具有直接影响，逐渐增加有效支撑集原子数后，重构信号达到了更低误差，显著优化了信号重构效果。经对比可以发现，将有效支撑集的原子数设定在1 时，曲线相对误差达到最大值，原子数设定在30 时，相对误差达到最低。以上测试结果表明，对于有效支撑集保持固定原子数的情况下，此时造成相对误差变化的因素主要为支撑集原子数。

2.2 算法重构性能仿真分析

为综合评价FBSOMP 算法的重构性能，运用正交匹配追踪（OMP）、FBSOMP、子空间追踪（SP）、压缩正交匹配追踪（SOMP）多种类型的算法完成重构仿真的对比分析，测定了100×256 高斯随机矩阵，步长保持5，控制信号稀疏度从0 增大至50。不同算法重构信号成功重构率，相对误差以及重构时间对比结果如图4～图6所示。

对图4～图6 进行分析可知，采用FBSOMP 算法进行处理时成功重构率达到了最大，把信号稀疏度提高至40 时，成功重构率只达到65%，相对其他算法发生了明显增大的现象；相对OMP、SP、SOMP的重构时间明显缩短；采用FBSOMP算法处理形成了相对误差最小的重构信号，已经非常接近初始信号。根据仿真结果可知，从重构过程的成功率、误差与处理时间方面分析，FBSOMP 算法都具备更优的重构结果。

图4 不同算法重构信号成功重构率对比Fig.4 Comparison of successful reconstruction rates of signals reconstructed by different algorithms

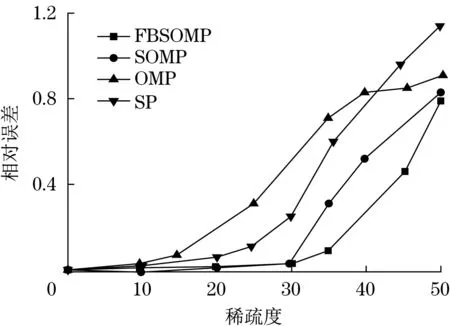
图6 不同算法重构时间对比Fig.6 Comparison of reconstruction time of different algorithms

图5 不同算法重构信号相对误差对比Fig.5 Comparison of signal relative errors reconstructed by different algorithms

3 试验验证

3.1 信号采集

本文主要针对旋转机械故障系统在运行阶段形成的电机轴承故障信号进行了测试分析。保持频率为12 kHz 的条件下进行采样，可知电机转速为1 790 r/min，外径尺寸0.177 5 mm。之后设计了测试方案验证驱动端轴承内圈、外圈与滚动体故障情况，轴承内圈和外圈原始故障信号测试结果如图7所示。

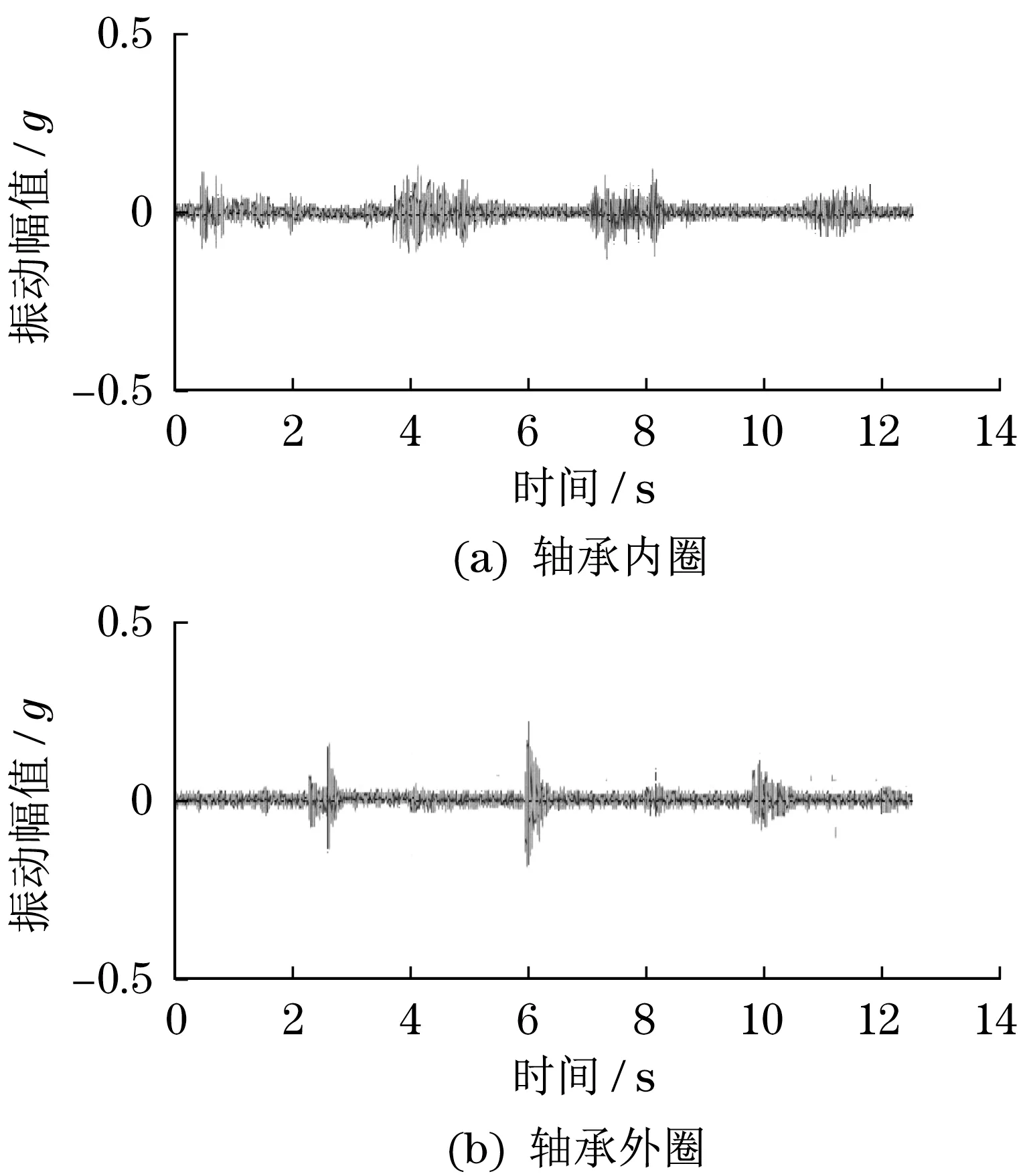
图7 轴承内圈和外圈原始故障信号Fig.7 Original fault signals of inner and outer rings of bearing

接着利用FBSOMP 算法完成信号重构过程，同时针对各条件下的测试情况果进行了对比。同时设置了两种经验值分块长度，包括64 和100，对每组条件分别经过100 次测试再计算得到平均结果。

3.2 轴承故障信号重构

保持压缩比为0.5的恒定值条件下实现驱动端轴承故障信号的重构。之后利用施稀疏变换的方式处理DCT 域故障信号，同时完成稀疏信号的重构计算，最后利用IDCT 方式对重构结果实现了转换的功能。

利用不同算法进行处理得到的相对误差及其重构时间测试结果见表2。依次针对各个故障齿轮区域进行了测试发现获得了与仿真结果接近的状态：以FBSOMP 算法计算得到的重构相对误差最小，与其他3 种算法相比能够更加快速达到重构的效果。

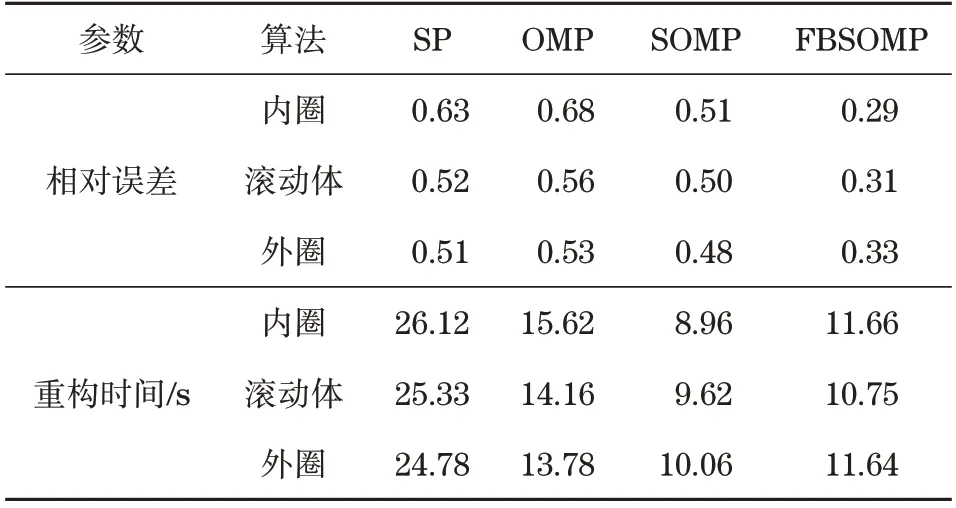
表2 不同算法轴承故障信号相对误差和重构时间Tab.2 Relative errors and reconstruction time of bearing fault signals with different algorithms

对上述测试结果进行分析可以发现，采用本文FBSOMP 算法有效保留了SOMP 算法不需要预估信号稀疏度的优点，由此达到更高的信号重构精度。

3.3 复合故障信号重构

采用本文方法开展复合故障预测，同时设置了机械故障模拟器对不同类型的故障信号进行了采集并对所得数据进行了测试分析。

不同算法混合故障信号原始图和信号重构结果如图8 所示。完成信号的重构后，可以达到准确重现初始信号故障特征的状态，有效实现了理想的匹配效果。不同算法复合故障信号相对误差和重构时间统计结果见表3。根据表3 可以看到，以SOMP 算法重构所需的时间最短，但相对误差达到最大，FBSOMP算法则可以实现高效运行的性能，由此大幅提高重构信号精度。

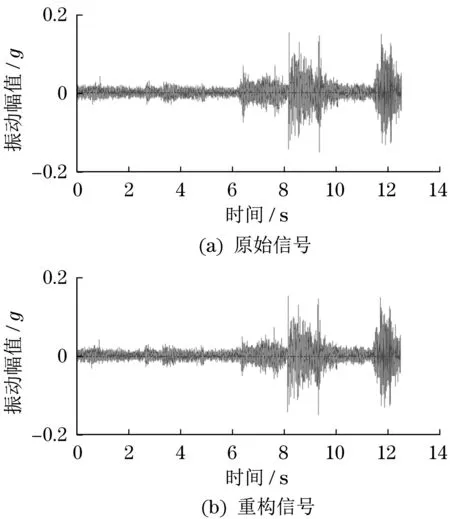
图8 不同算法混合故障信号原始图和信号重构Fig.8 Original diagram and signal recomposition of mixed fault signals with different algorithms

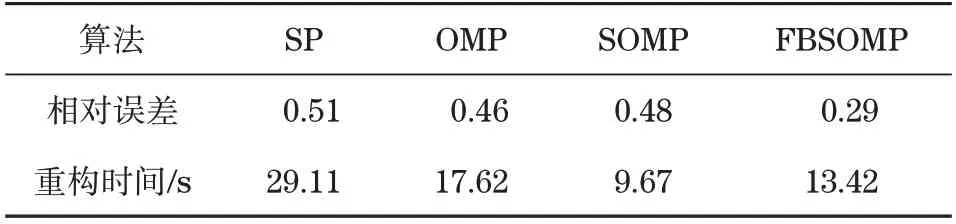
表3 不同算法复合故障信号相对误差和重构时间Tab.3 Relative errors and reconstruction time of compound fault signals of different algorithms

4 结论

（1）随着重构支撑集的有效支撑集原子数增加后，获得了跟初始信号误差更低的重构信号，重构信号达到了更低误差，显著优化了信号重构效果。相对OMP、SP、SOMP 的重构时间明显缩短，FBSOMP算法都具备更优的重构结果。

（2）利用不同算法处理相对误差及其重构时间测试结果得到，以FBSOMP 算法重构相对误差最小，能够更加快速达到重构的效果。

（3）信号重构可以达到准确重现初始信号故障特征的状态，有效实现了理想的匹配效果。FBSOMP算法则可以实现高效运行的性能，由此大幅提高重构信号精度。