装载机驾驶室非线性减振系统试验与优化
章 新 睢志伟 李占龙 秦 园 王 瑶 董 荻 赵钧铎
太原科技大学机械工程学院,太原,030024
0 引言
装载机行驶和作业的环境恶劣,剧烈振动严重影响驾驶员健康,因此其驾驶室振动一直是装载机研发中备受关注的问题[1-4]。装载机驾驶室的振动来源多,如行驶时来自地面的激励、作业时来自工作装置的激励,以及来自发动机的激励,故装载机驾驶室减振系统的设计应能满足不同工况的减振要求[5-10]。
目前,对于装载机和其他工程车辆的驾驶室阻尼减振研究,很多学者都是建立包含轮胎、悬架、驾驶室悬置、座椅悬挂的整机振动系统模型,以路面不平度为输入,分析与优化不同路况下的驾驶室减振性能,这类模型虽然适用范围广,但与驾驶室减振系统实际所受激励相差较大[11-15]。还有学者研究了发动机激振频率对驾驶室结构的共振影响,并以此对柔性化的驾驶室结构进行改进[16-18]。
本文首先通过实车试验得到不同工况下的装载机驾驶室系统各部位的振动信号,然后以车架振动信号为激励,建立驾驶室-座椅-人体的非线性阻尼系统模型,以驾驶室和座椅垂向加速度均方根值为目标进行多目标遗传算法优化,解决驾驶室振动过大和驾驶舒适性差的问题。
1 驾驶室-座椅-人体非线性减振系统模型
在M350-10kN型拉伸试验机上对原车驾驶室的橡胶隔振器进行静态单轴压缩测试,得出其力与位移的变化,如图1所示。
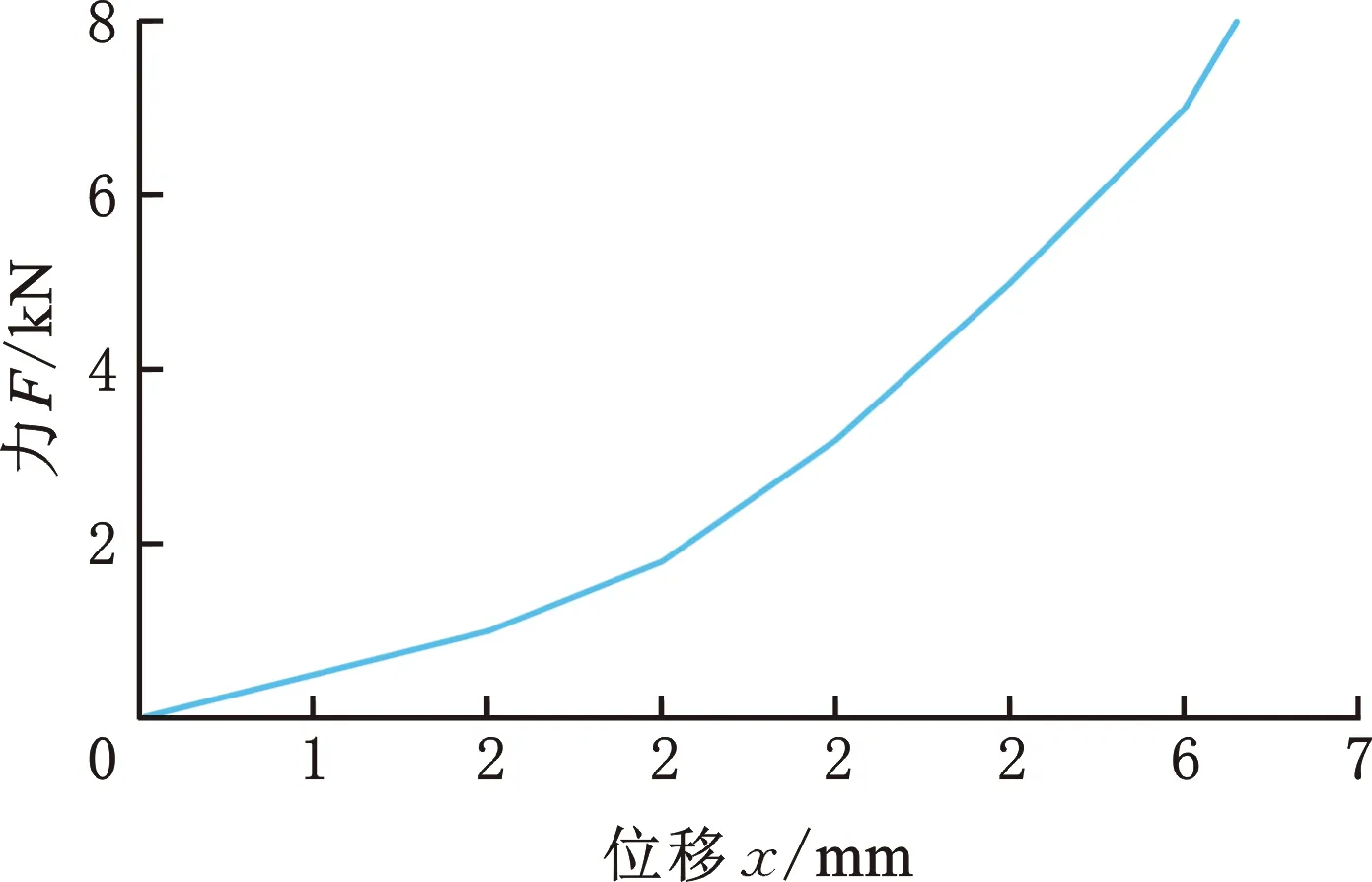
图1 橡胶隔振器测试曲线Fig.1 Test curve of rubber isolator
对厂家提供的装载机座椅进行静态测试,选择不同体重的测试人员乘坐并记录座椅的位移,多组数据拟合得到座椅的力-位移曲线如图2所示。
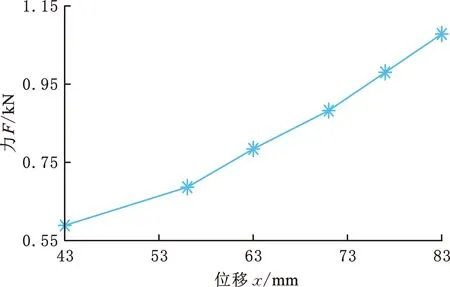
图2 座椅力和位移测试曲线Fig.2 Seat force and displacement test curve
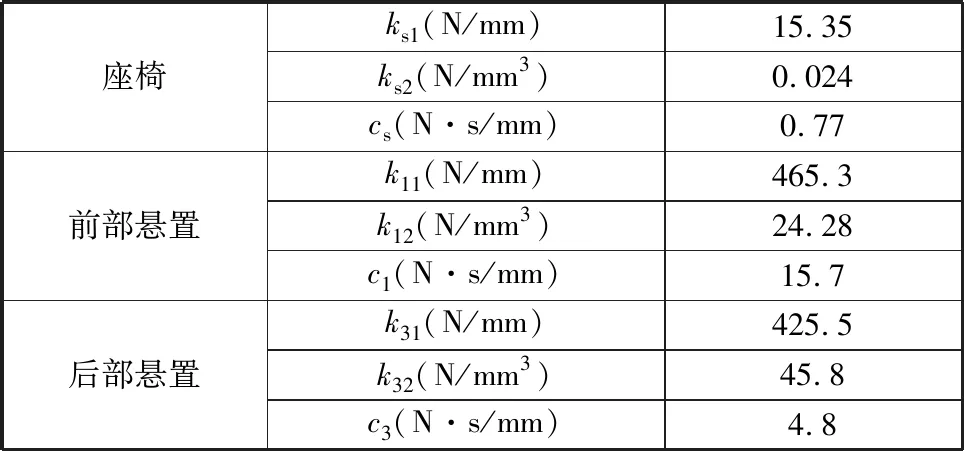
以某型装载机驾驶室为研究对象,该驾驶室系统主要参数见表1。输入激励来源于试验测试车架激励,然后通过驾驶室底部4个橡胶悬置传递到驾驶室地板、座椅、人体。同时建立驾驶室-座椅-人体的非线性阻尼系统模型,如图3所示,图中,zh、zs、zb分别为人体、座椅和车体的垂向位移;θ为俯仰角;φ为侧倾角;qi(t)为悬置的实测激励, 下标i=1,2,3,4分别表示左前、右前、右后、左后;Fs为座椅弹簧弹性力、cs为座椅阻尼系数;Fi为驾驶室悬置弹性力;ci为驾驶室悬置阻尼系数。
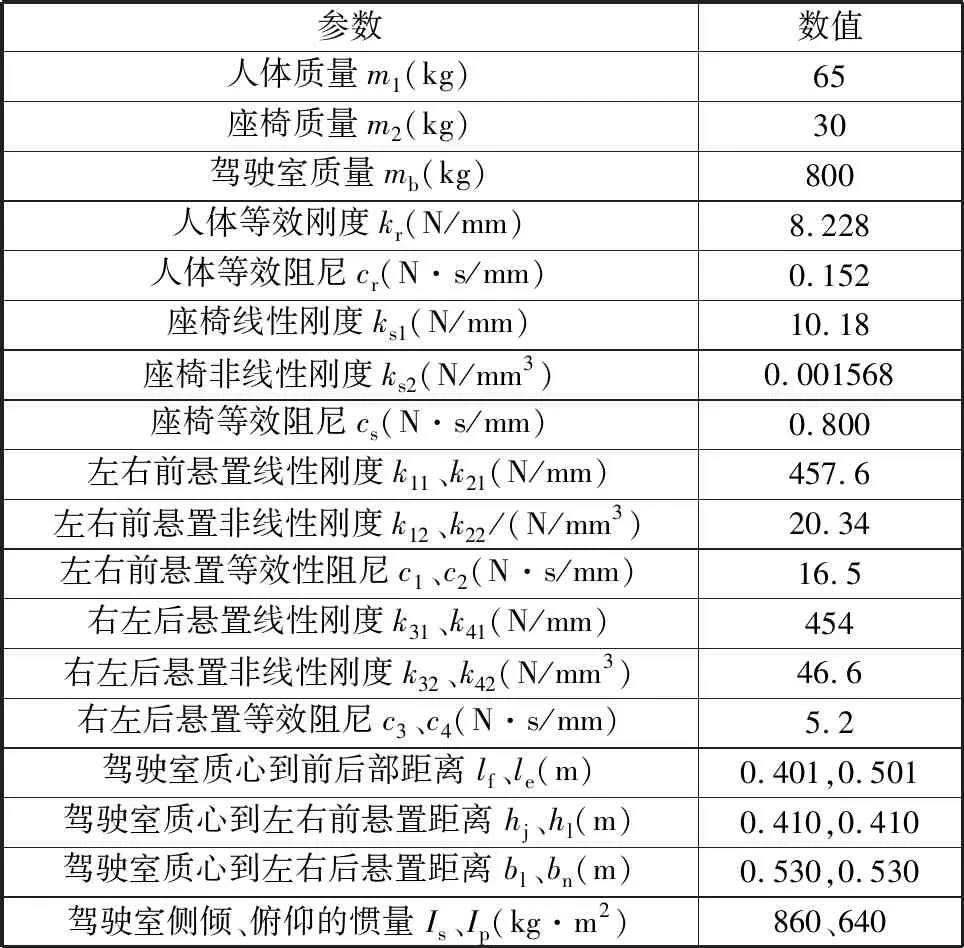
表1 模型参数
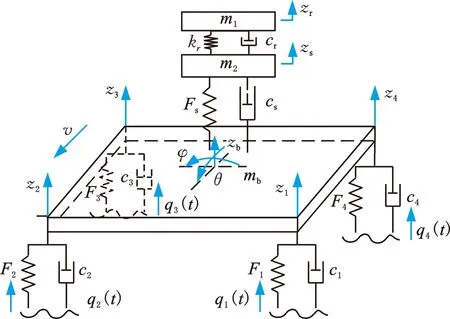
图3 驾驶室-座椅-人体非线性振动模型Fig.3 Nonlinear vibration model of cab-seat-human body
驾驶室-座椅-人体的非线性系统模型如下:
(1)
Fi=ki1(zi-qi(t))+ki2(zi-qi(t))3
(2)
Fs=ks1(zs-zb)+ks2(zs-zb)3
(3)
(4)
(5)
(6)
F4]=0
(7)
(8)
根据随机振动理论,建立4个输入、5个输出的系统,其中,Xε(ω)、Yi(ω)分别是Xε(t)和Yi(t)的傅里叶变换,Hεi(ω)为第ε个输入和第i个输出之间的频响函数,ω为圆频率。通过傅里叶变换,将输入、输出改写为矩阵形式:
(9)
(10)
则系统的频率响应矩阵为
假设驾驶室-座椅-人体的非线性阻尼系统模型的输入功率谱矩阵SX(ω)为4个输入的自谱与5个输出互谱构成的4×5阶输入功率谱矩阵:
5个输出的自谱与互谱构成的5×5阶输出功率谱矩阵为
则输出功率谱与输入功率谱的关系为
SY(ω)=H*(ω)SX(ω)HT(ω)
(11)
式中,H*(ω)为H(ω)的共轭矩阵。
驾驶室-座椅-人体的非线性阻尼系统模型的4个输入激励相互独立,那么只考虑座椅垂向的加速度时其输出功率谱密度函数可表示为
SZZ(f)=H*(f)SXX(f)HT(f)=
(12)
式中,f为频率;SXX(f)为五自由度模型的输入功率谱矩阵,SXX(f)=diag(S11,S22,S33,S44,S55);Sii(f)为驾驶室-座椅-人体的非线性阻尼系统模型频谱。
相对应的均方根值为
(13)
座椅垂向加速度的均方根值为
(14)
驾驶室垂向加速度的均方根值为
(15)
2 实车试验与模型验证
2.1 试验仪器及测点
本次测试在露天开阔的地方进行测试,测试试验具体仪器包括UT3400M动态信号分析系统、压电式IEPE加速度计,主要测试驾驶室悬置上下方、地板、座椅的加速度,测点布置如图4所示。

(a)前悬测点 (b)后悬测点

(c)座椅测点 (d)测试现场图图4 装载机驾驶室传感器布置图Fig.4 Sensor layout of loader cab
2.2 试验数据分析与模型验证
综合考虑轮式装载机使用和行驶的特点,试验选择一段典型的工地路面,重复测量3次,对测试得到的数据进行预处理,将处理后的车架测试数据作为输入激励(图5),然后将悬置下方、上方及座椅振动数据进行快速傅里叶变换(图6)。对驾驶室和座椅的减振效果进行初步分析,发现行驶和作业时的座椅振动有放大。
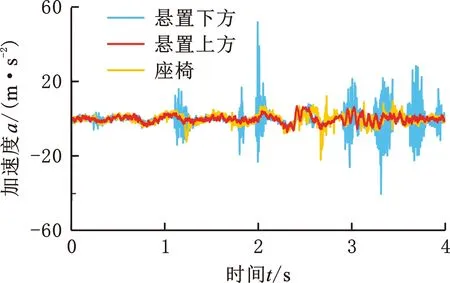
图5 行驶工况下的垂向振动加速度Fig.5 Sagging acceleration under driving conditions
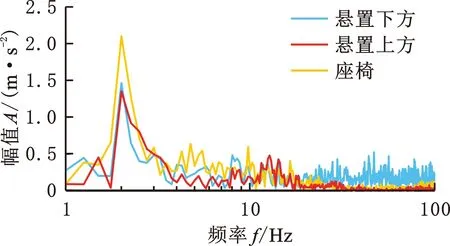
图6 行驶工况下的垂向加速度频域曲线Fig.6 Frequency domain curve of drooping acceleration under driving conditions
将测试所得的车架激励作为驾驶室-座椅-人体非线性系统模型的输入,则得到行驶和作业工况下的驾驶室和座椅的垂向加速度试验曲线和仿真曲线,如图7~10所示。
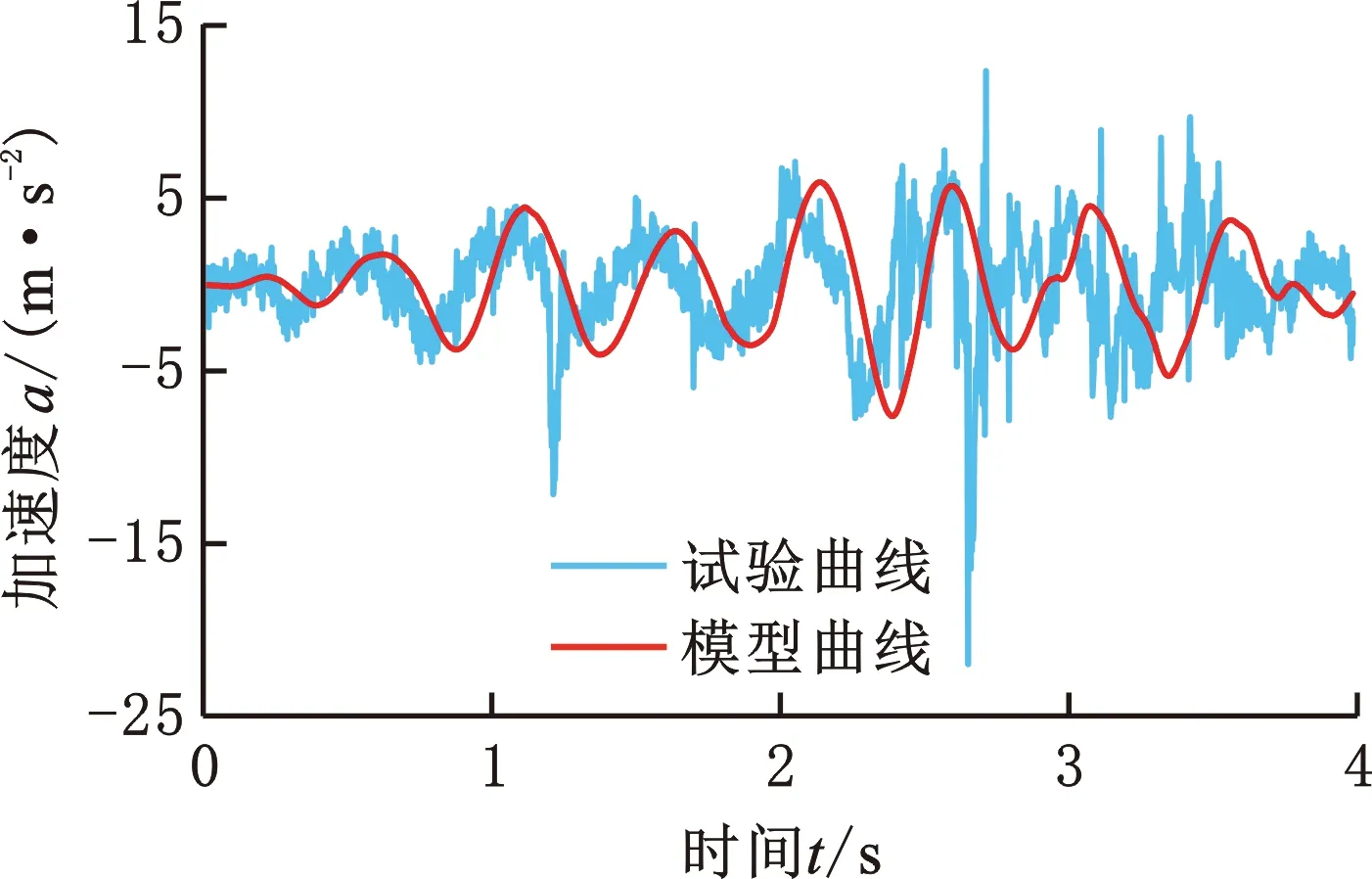
图7 行驶工况下的座椅垂向加速度Fig.7 Vertical acceleration of seat under driving conditions
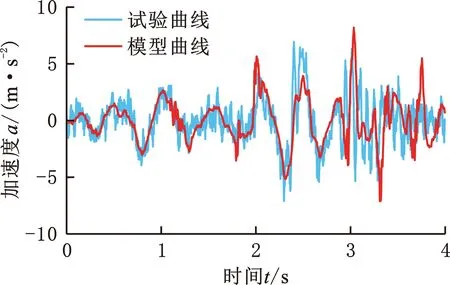
图8 行驶工况下的驾驶室垂向加速度Fig.8 Vertical acceleration of cab under driving conditions
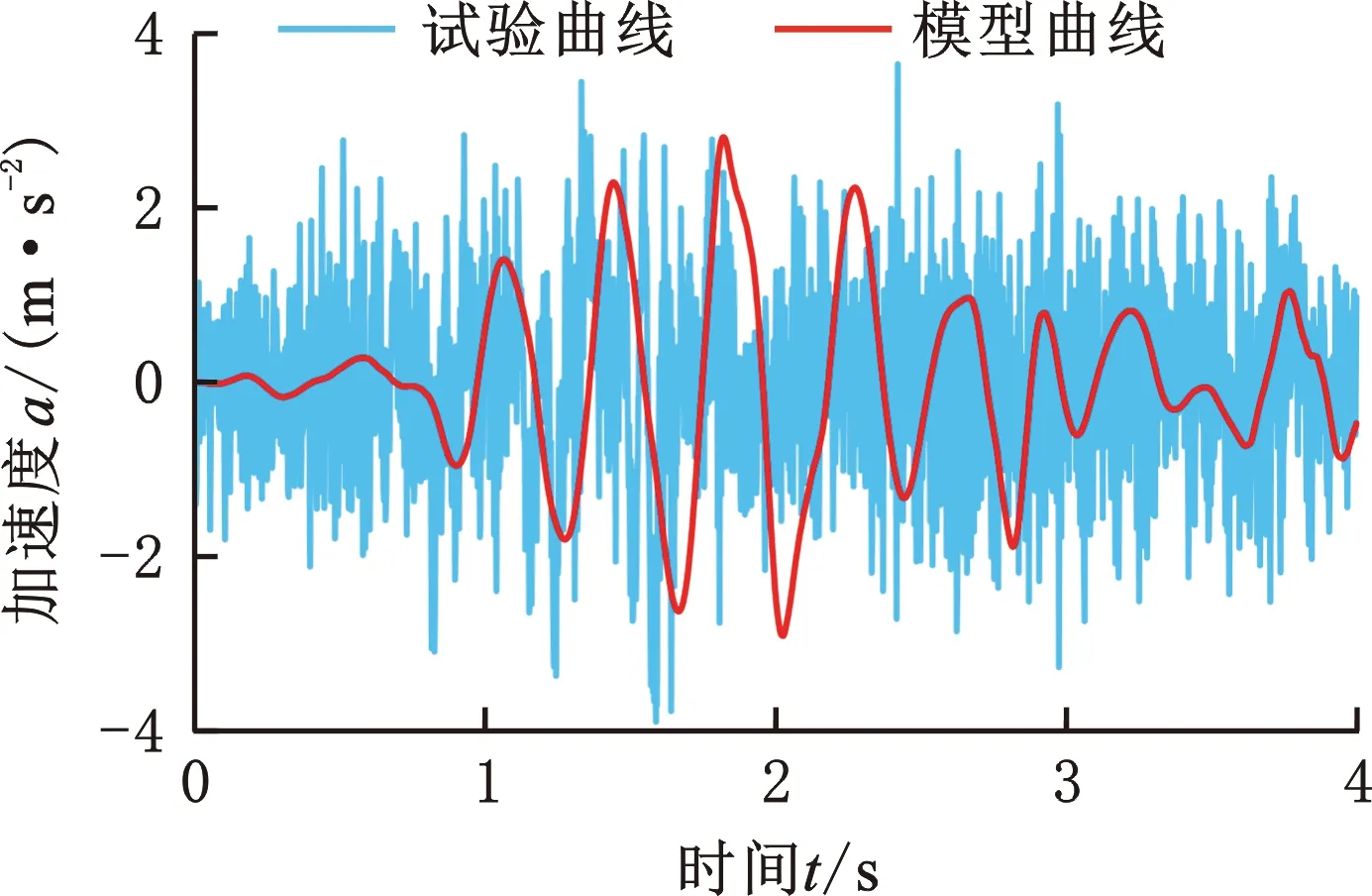
图9 作业工况下的座椅垂向加速度Fig.9 Vertical acceleration of working seat under working conditions
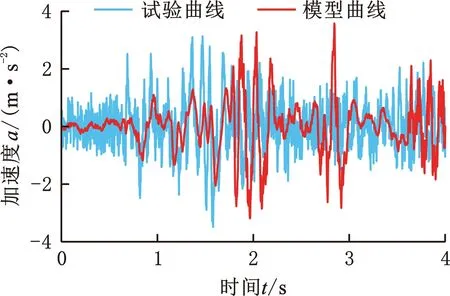
图10 作业工况下的驾驶室垂向加速度Fig.10 Vertical acceleration of working cabunder working conditions
由表2可知,各测点的测试值与仿真值的最大均方根误差均在6 % 以内,说明仿真模型的计算精度满足工程需求;座椅比驾驶室的加速度均方根值大,说明座椅设置不合理;高速行驶时,驾驶室及座椅的垂向振动比作业时的大得多。高速行驶时,驾驶室减振系统的振动过大,而作业时的加速度均方根值不到高速行驶的一半,所以本文的优化设计只考虑行驶工况。
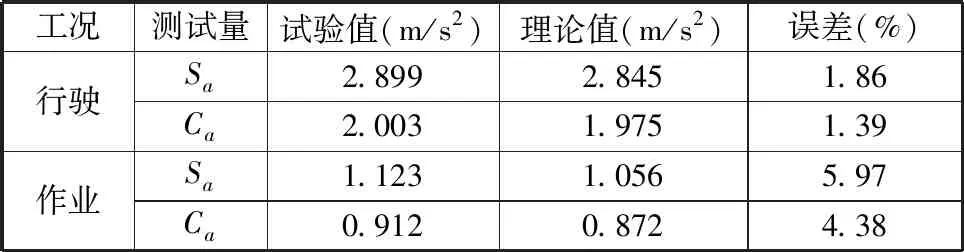
表2 试验与理论模型的加速度均方根值
3 遗传算法多目标优化
3.1 遗传算法介绍
遗传算法是一种进化算法,它从任一初始种群出发,通过随机选择、交叉和变异操作,产生一群更适合环境的个体,使群体进化到搜索空间中越来越好的区域,这样一代一代不断繁衍进化,最后收敛到一群最适应环境的个体,从而求得问题的优质解[19-22]。算法具体步骤见图11。
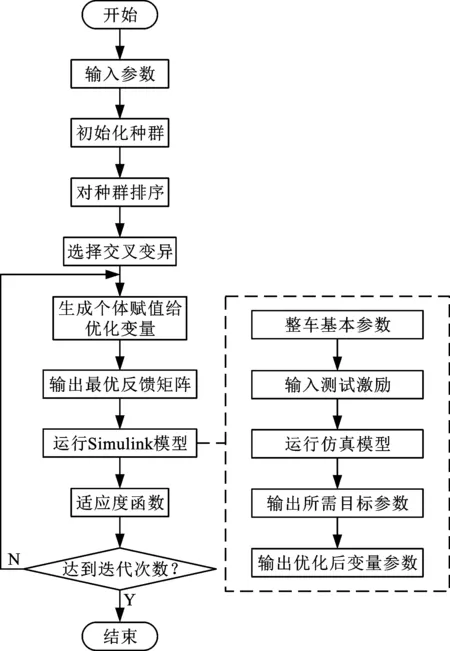
图11 遗传算法具体步骤Fig.11 Specific steps of genetic algorithm
3.2 优化数学模型
由于驾驶室质心与左右橡胶悬置的距离相等,故左右橡胶悬置的参数相同。优化模型的变量A=(ks1,ks2,k11,k12,k31,k32,cs,c1,c3),选择驾驶室和座椅的垂向加速度的均方根值为优化目标。多目标优化设计问题数学模型一般形式可以写成以下函数:
(16)
设计的控制参数取值范围如下:
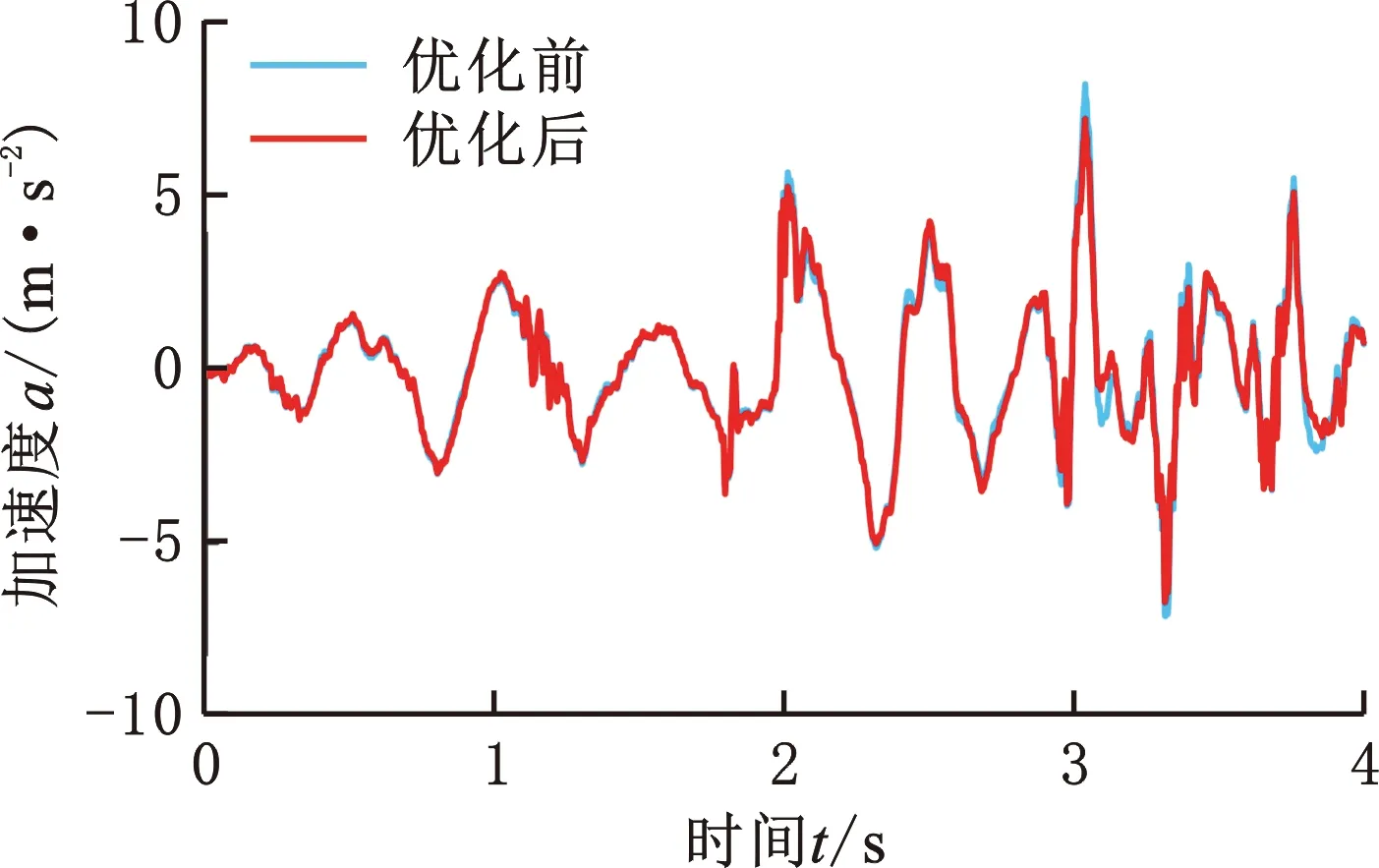
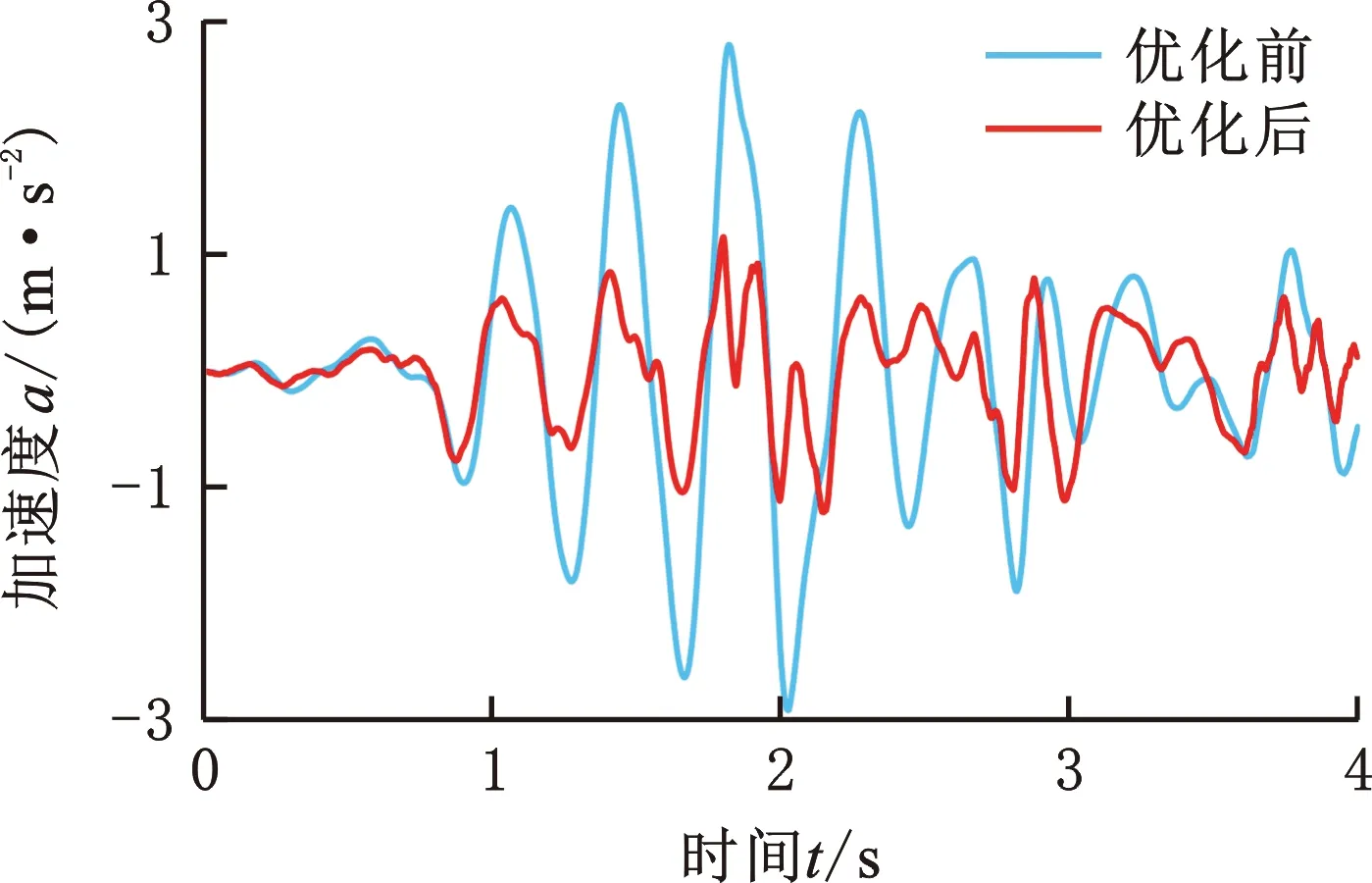
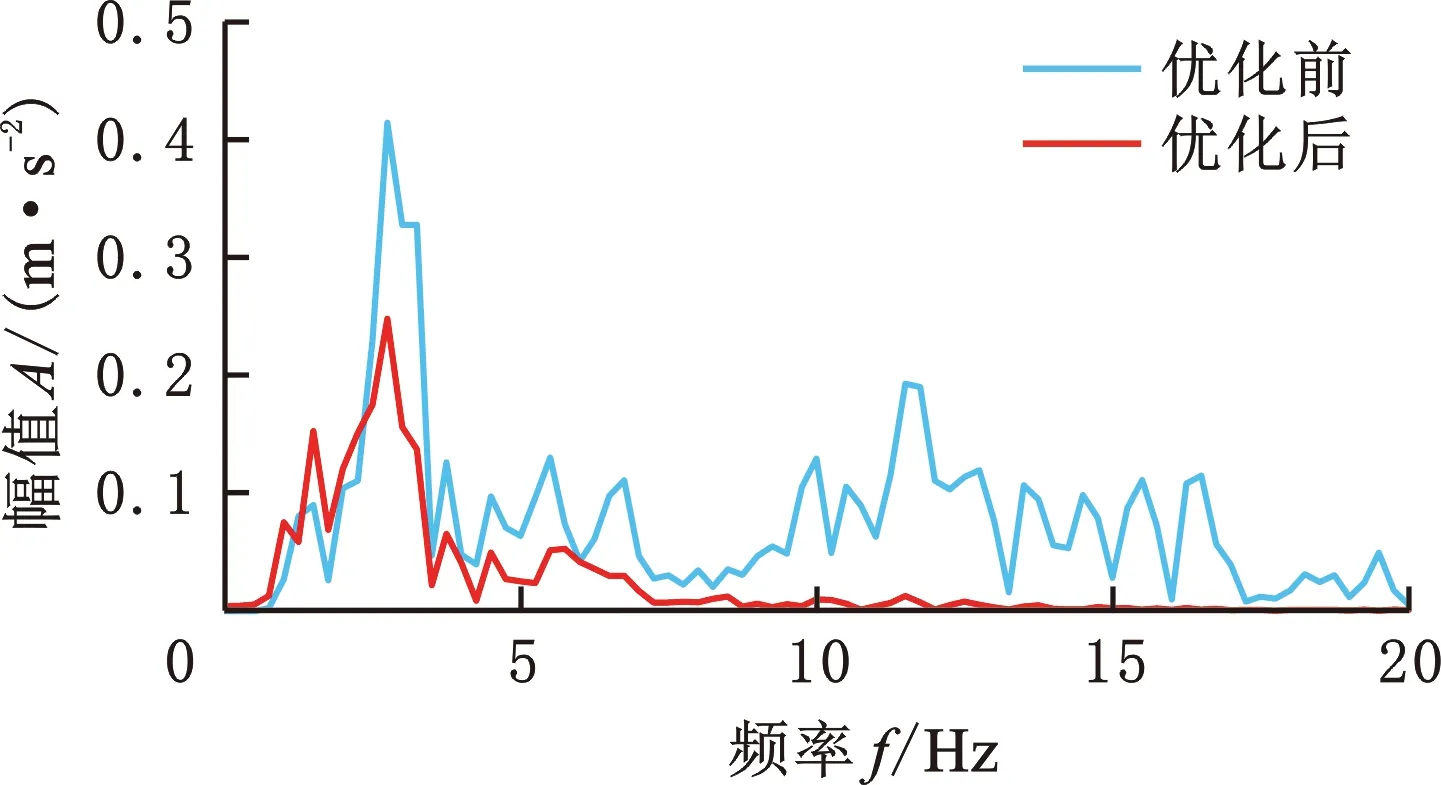
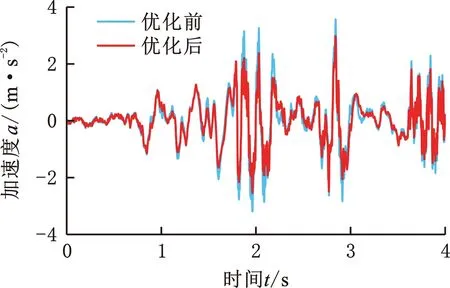
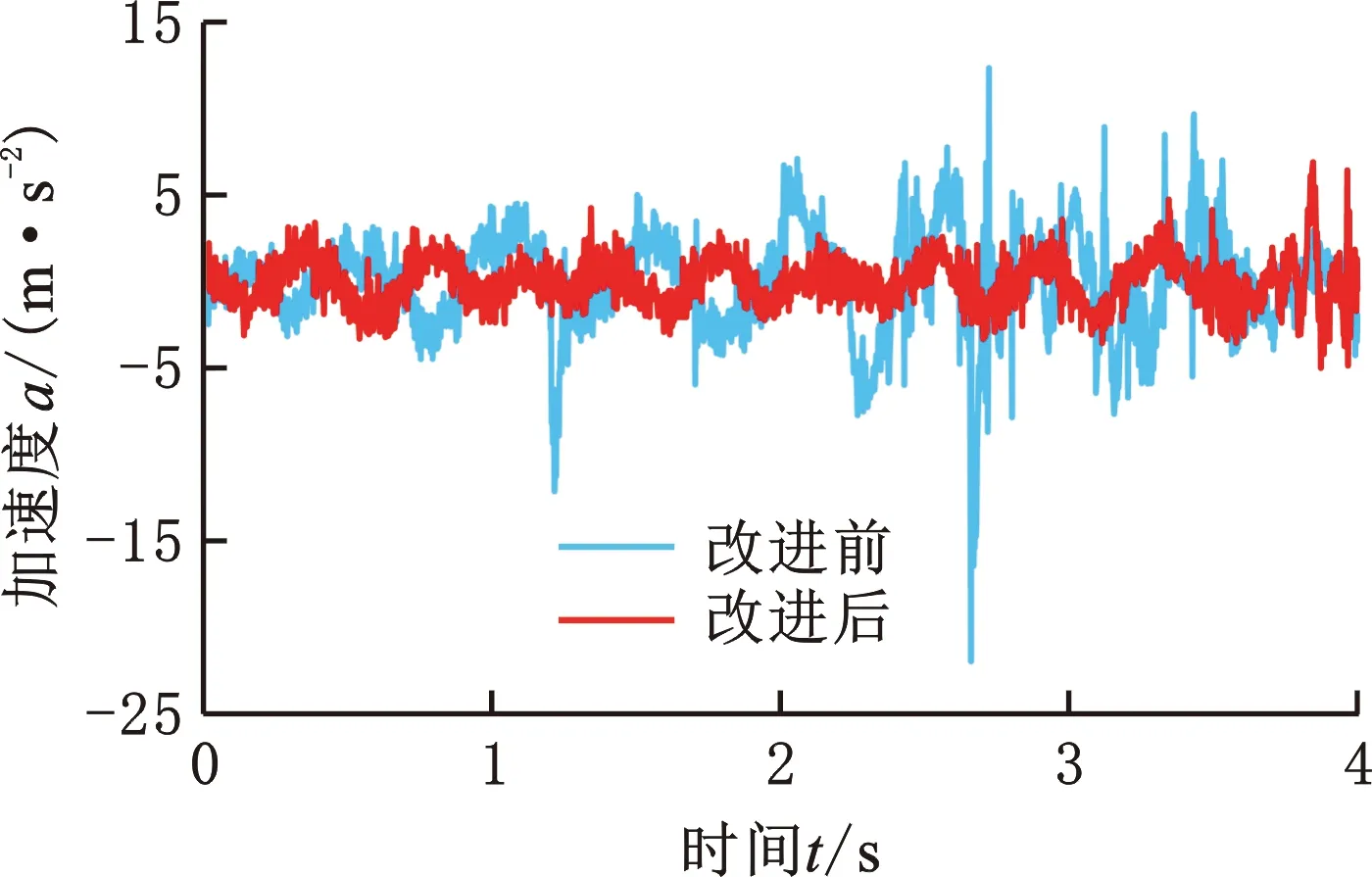
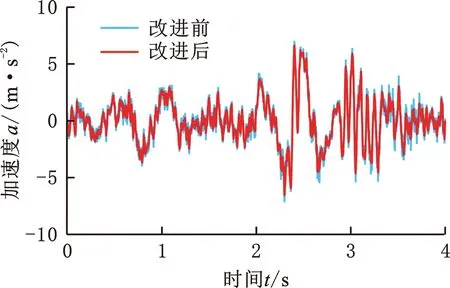
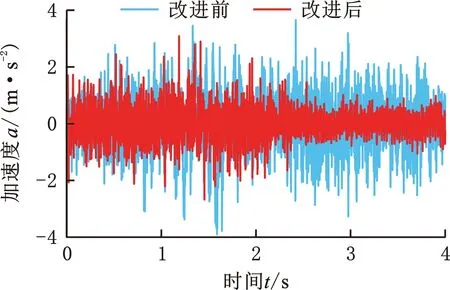
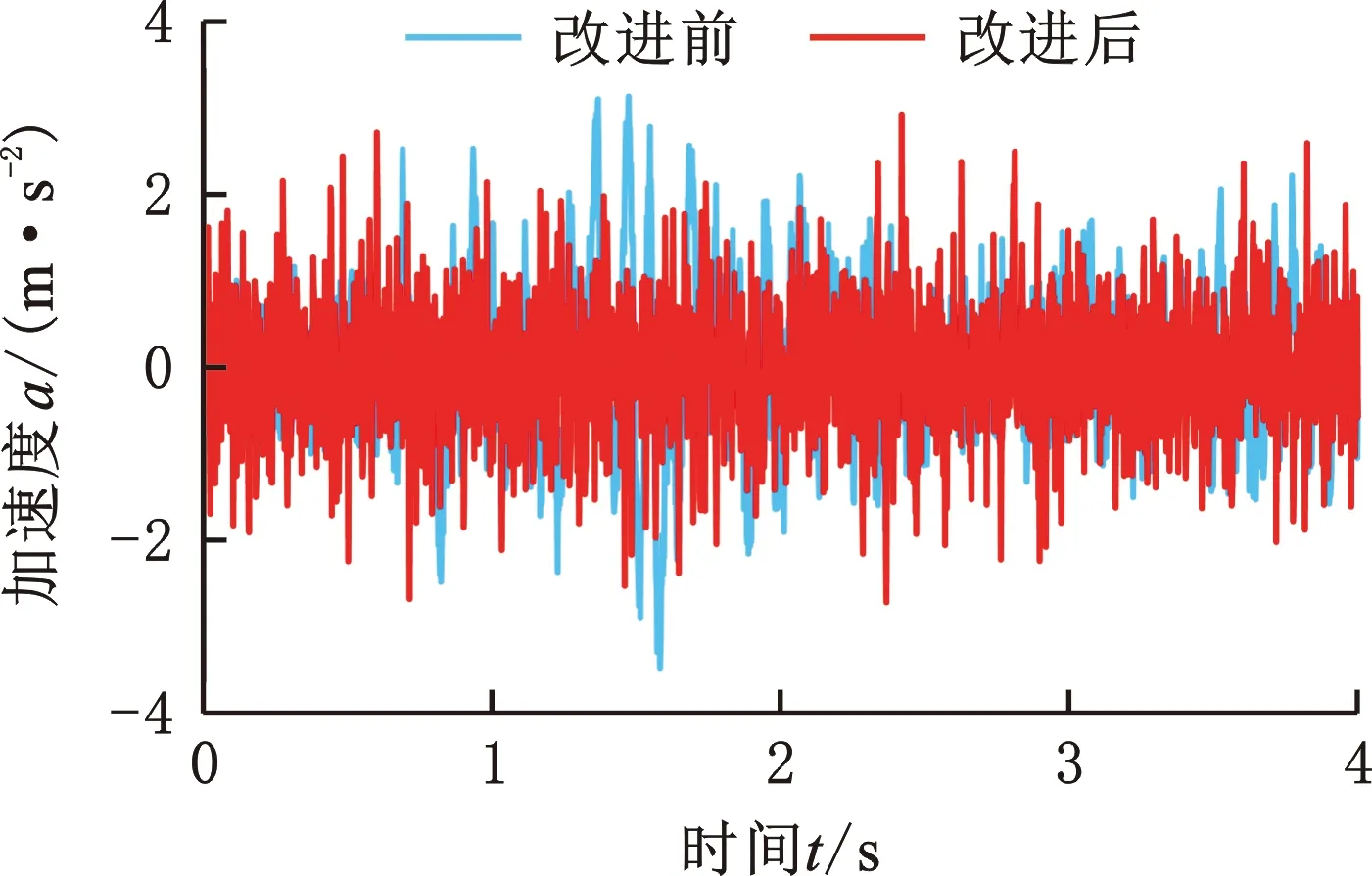
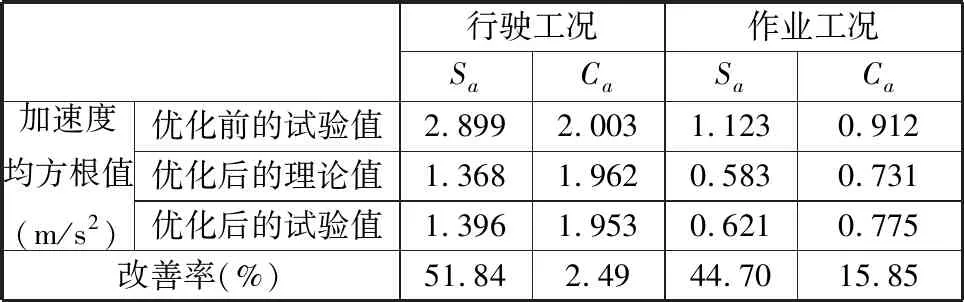
30 N/mm -1 N/mm3 400 N/mm 10 N/mm3 300 N/mm 30 N/mm3 0.3 N·s/mm 12 N·s/mm 3 N·s/mm 设定多目标遗传算法的种群个体数目为100,最优前端个体系数为0.3,变量个数为6,最大进化代数为100,停止代数为100,适应度函数选择10-6。优化得到的Pareto前沿如图12所示,可以看出,驾驶室和座椅的垂向加速度均方根值在行驶工况下是相互矛盾的,一个目标的最优要以牺牲另一个目标为代价。 图12 行驶工况下的Pareto前沿图Fig.12 Pareto frontier diagram under driving conditions 在工程应用中,驾驶员的舒适性尤为重要,故优化结果中的座椅垂向加速度均方根值所占权重应更大。以选择座椅权重为0.9、驾驶室权重为0.1的一组权重系数为例,根据图12和优化后的多目标结果的解集,选出符合要求权重的一组数据,见表3。 表3 不同权重系数下的多目标优化结果 将优化后的结果分别代入行驶工况、作业工况的阻尼模型,得到优化前后的驾驶室和座椅的振动加速度,如图13~18所示。通过该模型仿真运算得出装载机驾驶室的垂向最大位移8.6 mm、座椅的垂向最大位移110 mm。 图15 行驶工况下的驾驶室垂向振动加速度Fig.15 Vertical vibration acceleration of cab under driving conditions 图16 作业工况下的座椅垂向振动加速度Fig.16 Vertical vibration acceleration of seat under working conditions 图17 作业工况下的座椅垂向加速度频域曲线Fig.17 Frequency domain curves of seat vertical acceleration under working conditions 图18 作业工况下的驾驶室垂向振动加速度Fig.18 Vertical vibration acceleration of cab under working conditions 由图14、图17可以看出,优化后的加速度频域曲线峰值有明显减小;由图13、图15、图16、图18可以看出,优化后的加速度有所减小。 按照表3所示参数对驾驶室悬置和座椅悬架进行改进。改进后,车辆以相同车速进行试验,以驾驶室底板和座椅的垂向加速度均方根值为驾驶室系统振动特性主要评价指标;测试仪器采样频率为512 Hz,优化后的实车试验结果如图19~图22所示。 图19 行驶工况下的座椅垂向振动Fig.19 Vertical vibration of seat under driving conditions 图20 行驶工况下的驾驶室垂向振动Fig.20 Vertical vibration of cab under driving conditions 图21 作业工况下的座椅垂向振动Fig.21 Vertical vibration of seat under working conditions 图22 作业工况下的驾驶室垂向振动Fig.22 Vertical vibration of cab under working conditions 由表4可知,优化后的理论值和试验误差为3.28%。改进后,行驶工况下的座椅加速度均方根值误差减小了51.84%,驾驶室加速度均方根值减小了2.49%;作业工况下,座椅加速度均方根值减小了44.70%,驾驶室加速度均方根值减小了15.85%。优化后的驾驶室减振系统有所改善。 表4 不同工况各部位的加速度均方根值 (1)通过建立驾驶室-座椅-人体的非线性振动系统模型,并以实测的车架振动信号为模型激励,计算得到模型结果并与实车试验结果对比,二者间的最大误差在6% 以内,表明该模型可满足工程精度需求。 (2)实车试验发现,行驶工况下的装载机驾驶室振动比作业和静止工况的大得多,且座椅的加速度均方根值大于驾驶室的相应值,座椅振动明显放大。 (3)实车试验显示,优化后的驾驶室垂向加速度均方根值减小了2%~16%,座椅垂向加速度均方根值减小了48%~52%,优化提高了驾驶室的减振性能和座椅的舒适性。3.3 优化结果
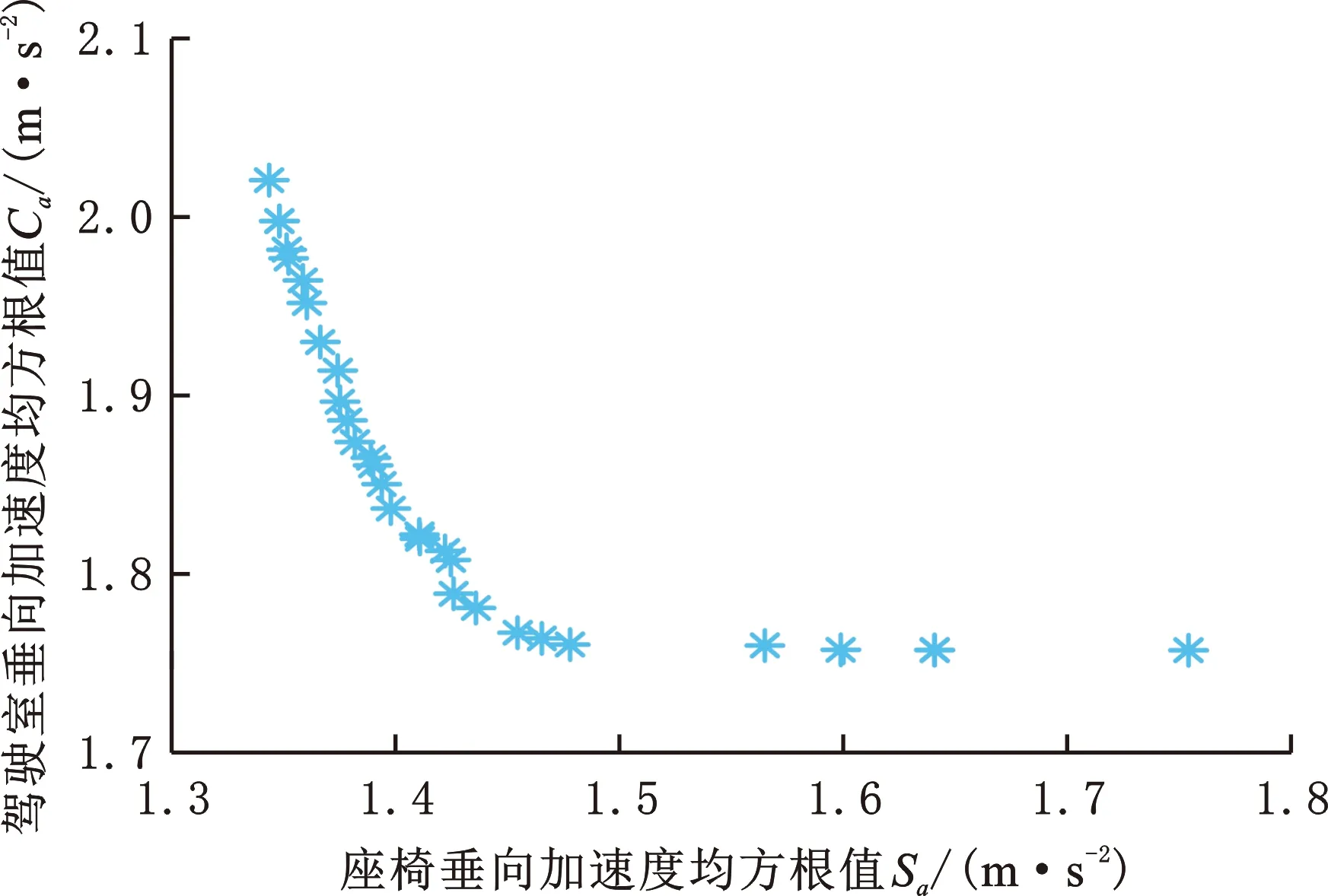
4 优化结果验证
5 实车验证
6 结论

