小交错角面铣准双曲面齿轮副的几何设计与啮合特性
刘思远 宋朝省 朱才朝
重庆大学机械传动国家重点实验室,重庆,400044
0 引言
空间小交错角齿轮传动能克服极端条件下的动力换向复杂结构效率低、成本高等问题,具有体积小、传动精度高、可靠性高等优点,在高速船舶动力倾角传动、四驱汽车动力分动倾角传动等领域有着不可替代的优势与广阔应用前景。现有的空间小交错角传动部件主要为渐开线变厚齿轮和小交错角准双曲面齿轮。
相比于渐开线变厚齿轮,准双曲面齿轮具有重合度大、啮合特性可预置、单轮节锥角不受限等优点,在正交空间传动领域具有极其广泛的应用,但在小交错角空间传动领域,其交错角与偏置距等参数极端变化导致其齿形演化与啮合机理复杂关联不清,传统基于正交安装的准双曲面齿轮设计方法不适用,严重制约了其发展与应用。
目前,国内外对小交错角准双曲面齿轮传动的研究尚在起步阶段。DOONER等[1]提出了准双曲面齿轮在小交错角传动领域应用的构想。STADTFELD[2]对小交错角准双曲面齿轮几何参数进行了初步的推导。YANG等[3]基于局部综合法对小交错角准双曲面齿轮加工参数计算方法进行了初步探索。LIU等[4]对小交角准双曲面齿轮基本几何参数取值范围进行了探讨,并绘制了封闭图。DOONER[5]基于广渐曲线提出了适用于0°~90°工况的准双曲面齿轮设计方法。综上可知,目前小交错角准双曲面齿轮仍处于探索阶段,缺乏系统性的几何设计流程、加工参数计算标准以及啮合特性分析方法。
本文基于准双曲面齿轮啮合机理,推导了考虑空间三大几何关系的小交错角准双曲面齿轮几何参数设计流程;改进局部综合法,提出了小交错角极端工况下考虑啮合特性预置的机床加工参数计算方法;提出了小交错角准双曲面齿轮副的一般加工方法;通过轮齿接触分析与承载分析,研究了外载荷对齿面啮合特性的影响,并验证了上述设计方法的正确性;设计、制造、装配了小交错角齿轮传动原理样机。
1 小交错角准双曲面齿轮的几何设计
空间交错轴传动的相对运动是螺旋运动,假想齿面毛坯母线绕齿轮回转轴旋转时形成一对单叶双曲面,如图1所示,将两单叶双曲面接触区域定义为瞬时接触轴。
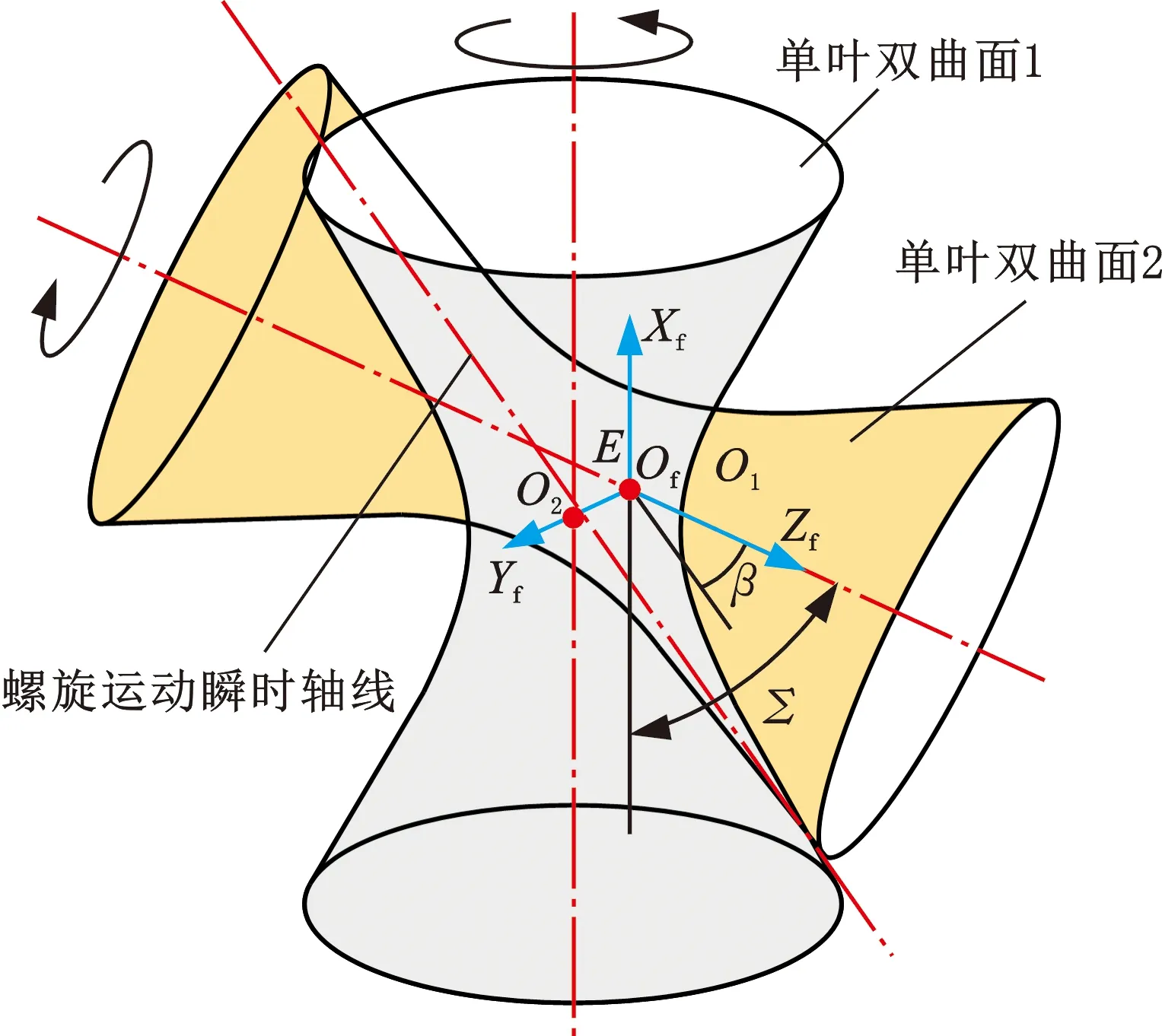
图1 空间单叶双曲面副位置关系Fig.1 Spatial position relationship between uniparted hyperboloids
2个单叶双曲面回转轴的距离定义为E,两轴线的交错角定义为Σ,2个单叶双曲面回转角速度比为m21。在2个单叶双曲面交错点上建立全局坐标系Sf(xf,yf,zf),由此,可求得螺旋运动的瞬时轴线上任意点在坐标系Sf下的坐标分量:
(1)
(2)
式中,u为参变量,表示瞬时轴线上任意点的位置;β为瞬时轴线与全局坐标系Sf中Z轴的夹角。
将全局坐标系Sf中的瞬时轴线上任意点转换至各原始坐标系中,可得单叶双曲面1和2的表达式:
(3)
(4)
式中,θ1、θ2分别为单叶双曲面1和2的回转角度控制参数。
轮齿齿宽一定时,可将齿面视为单叶双曲面上的任意截取段,并以回转圆台来替代。由此可将空间单叶双曲面的瞬时接触问题转换为空间节圆锥副的相切问题,基于式(3)、式(4)可建立单叶双曲面副实体模型,如图2所示。由于截取长度很短,因此可将切点M看作为瞬时轴线上任意一定点。
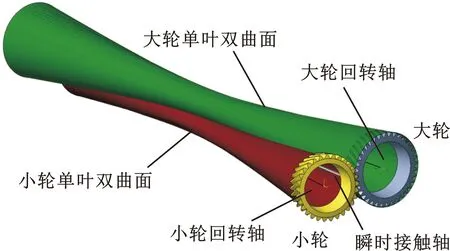
(a)小轮、大轮与瞬时接触轴的空间位置关系
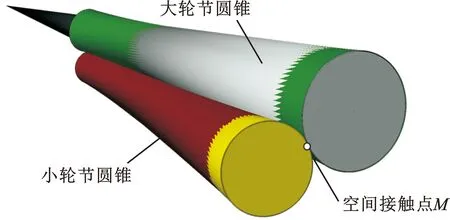
(b)切触点与节圆锥副的空间位置关系图2 单叶双曲面与节圆锥几何转化关系Fig.2 Translated relationship between uniparted hyperboloids and pitch cones
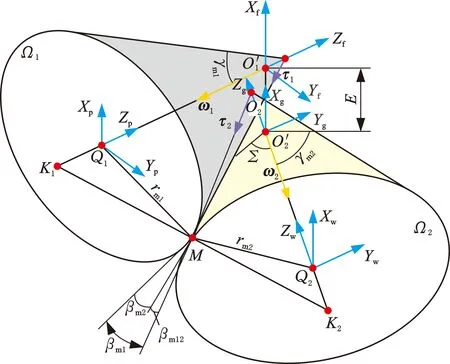
图3 小交错角准双曲面齿轮节圆锥数学模型Fig.3 Mathematical model of pitch cone of hypoid gear in low crossed shaft angle
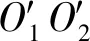
基于两节圆锥螺旋角的差值βm12可定义小交错角准双曲面齿轮的第一几何关系:
τ1·τ2=|τ1||τ2|cosβm12
(5)
τ1=(sinγm1cosθ1,sinγm1sinθ1,cosγm1)
(6)
τ2=(sinγm2cosθ2,sinγm2cosΣsinθ2,sinγm2sinΣsinθ2+cosΣcosγm2)
(7)
化简可得
(8)
基于切点M处的相对运动速度,可求得小交错角准双曲面齿轮第二几何关系:
(9)
式中,i12为齿轮副传动比;rm1、rm2分别为小轮和大轮的参考点半径。
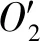
(10)
(11)
式中,l为直线段K1K2的长度。
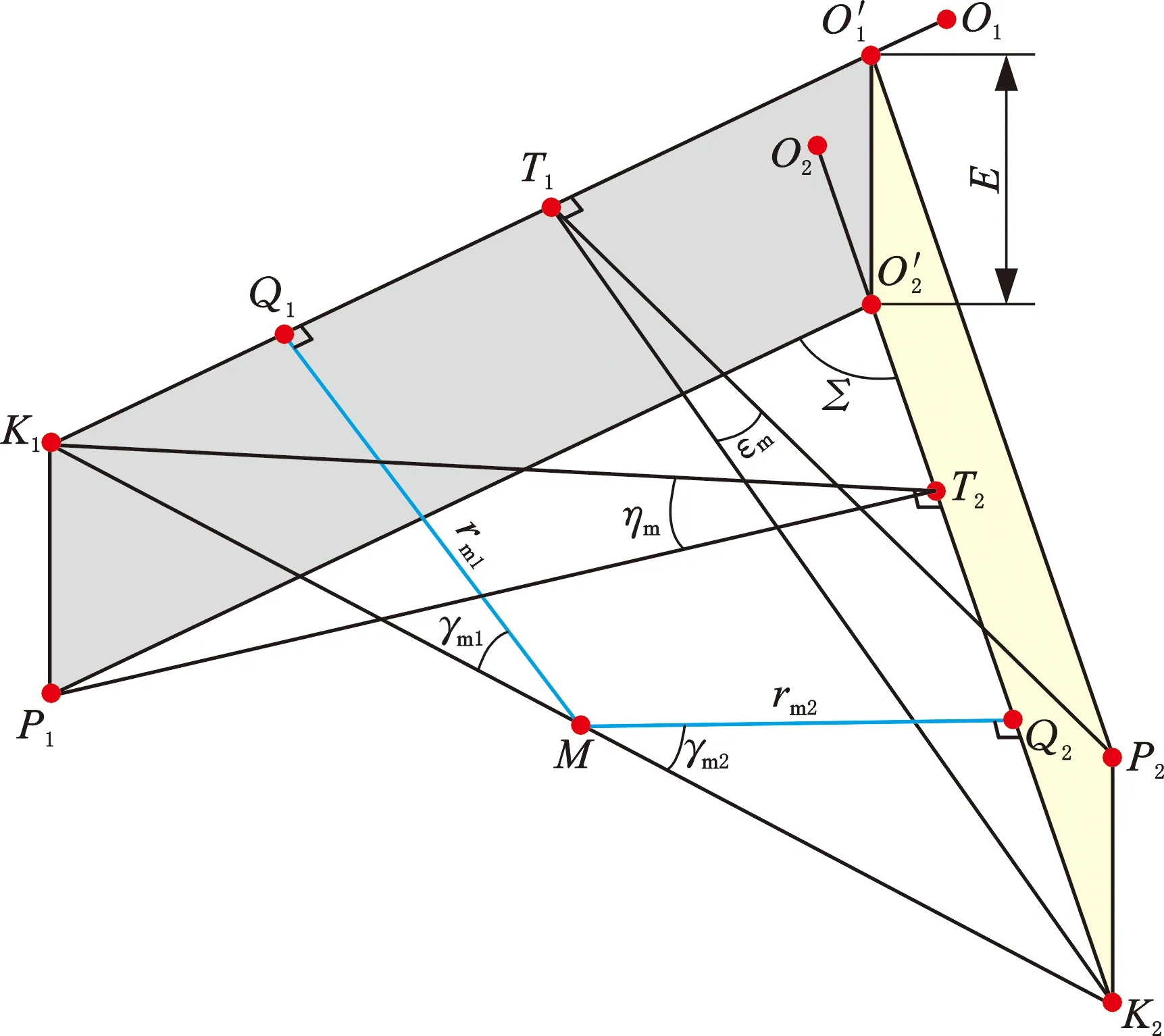
图4 小交错角准双曲面齿轮空间几何关系Fig.4 Geometric relationship of hypoid gear in low crossed shaft angle
基于节圆锥副的空间几何关系式,联立式(10)、式(11),可导出小交错角准双曲面齿轮第三几何关系:
(12)
准双曲面齿轮齿廓在节平面内存在极限单位法向量,极限单位法向量与节平面法向量之间的夹角极限压力角为
(13)
基于成形法加工的准双曲面齿轮大轮在齿面创成过程中,齿向曲率应与刀盘曲率完全一样,该齿向曲率定义为极限曲率,具体表达式如下:
(14)
(15)
(16)
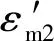
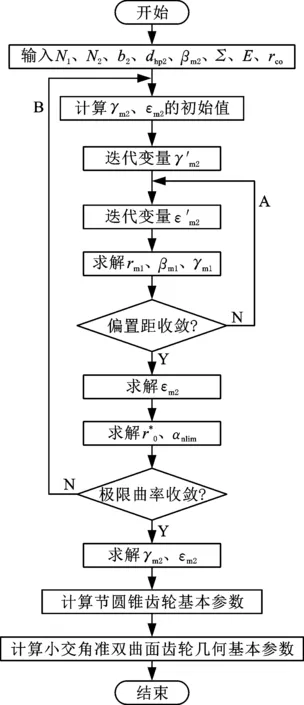
图5 小交错角准双曲面齿轮几何参数设计流程图Fig.5 Geometric parameter design flow chart of hypoid gear in low crossed shaft angle
2 小交错角面铣削准双曲面齿轮的局部综合法优化
小交错角面铣准双曲面齿轮的加工依托于现有铣齿机,齿面创成机理如图6所示[6]。ric、roc、rmc分别为刀盘的内刀半径、外刀半径和名义半径。基于展成法的小轮通过机床的9个加工参数(刀倾角Tr1i、刀转角Wr1i、径向刀位Sr1i、角向刀位Or1i、垂直轮位Er1i、水平轮位Ar1i、床位Br1i、机床根锥角Mr1i、滚比Vr1i)控制刀盘与齿面的空间位置,完成齿面的创成过程,其中,i为c表示小轮凹面,i为v表示小轮凸面。基于成形法的大轮齿面通过机床的5个加工参数(径向刀位Sr2、角向刀位Qr2、水平轮位Ar2、床位Br2、机床根锥角Mr2)控制。
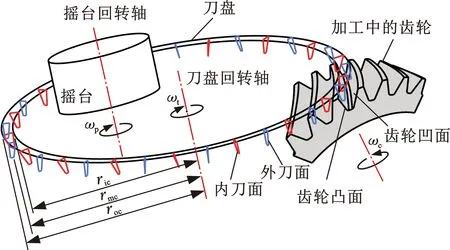
图6 准双曲面齿轮齿面创成机理Fig.6 Generated methodology of gear flank of hypoid gear
摇台回转角速度ωp、刀盘回转角速度ωt以及齿轮毛坯回转角速度ωc的关系如下:
(17)
式中,Zi、Zp、Z0分别为齿轮齿数、冠轮齿数(通常情况不为整数)和刀盘头数。
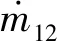
(18)
式中,Rm2为大轮节锥距;zm2为大轮锥顶超过交错点的距离。
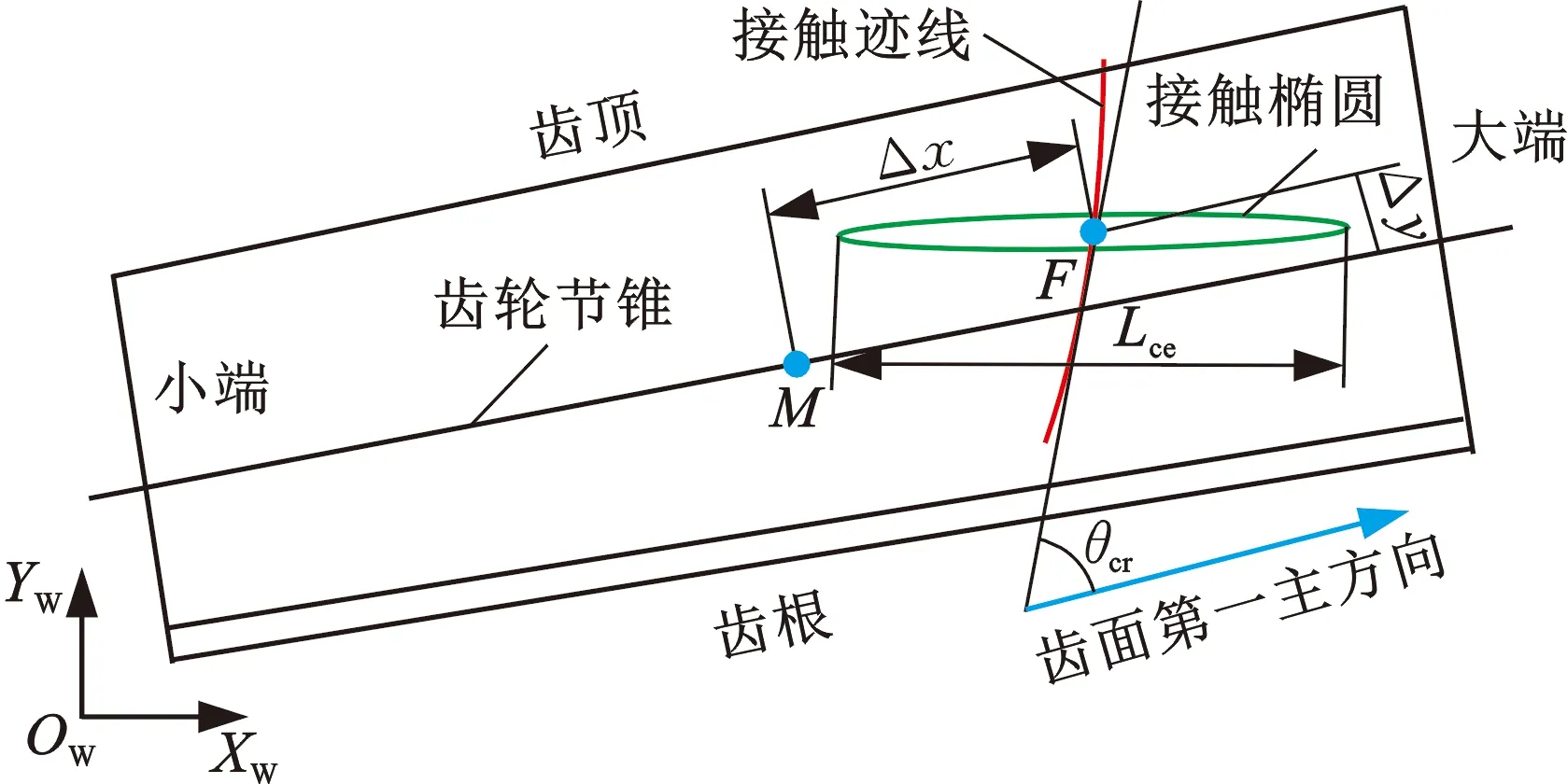
图7 基于局部综合法的啮合特性预置Fig.7 Preset mesh behavior based on the local synthesis method
局部综合法的主要应用对象是正交弧齿锥齿轮,但小交错角工况下,准双曲面齿轮对齿轮设计参数极其敏感,齿轮凹凸面加工参数差异大会导致两齿面在齿轮根部过渡区域出现台阶,直接影响轮齿的弯曲强度。形成过渡区错层的根本原因是局部综合法的机床根锥角计算方法对小交错角工况不适用。基于此,提出针对小交错角的机床根锥角修正方法。
如图8所示,将齿轮凹凸面离散化成m×n的点集。将齿轮凸面和凹面根部点定义为RAVk和RACk(k=1,2,…,n),它们在小轮齿面原始坐标系下的标分别为(xAVk,yAVk,zAVk)和(xACk,yACk,zACk)。将齿轮凹凸面根部点RAVk与RACk投影至投影面Q,RACk、RAVk在投影面Q的投影分别为点Ck和Vk。齿轮凹凸面齿根部分投影线C1Cn、V1Vn与回转轴线的夹角γmc、γmv分别为
(19)
(20)
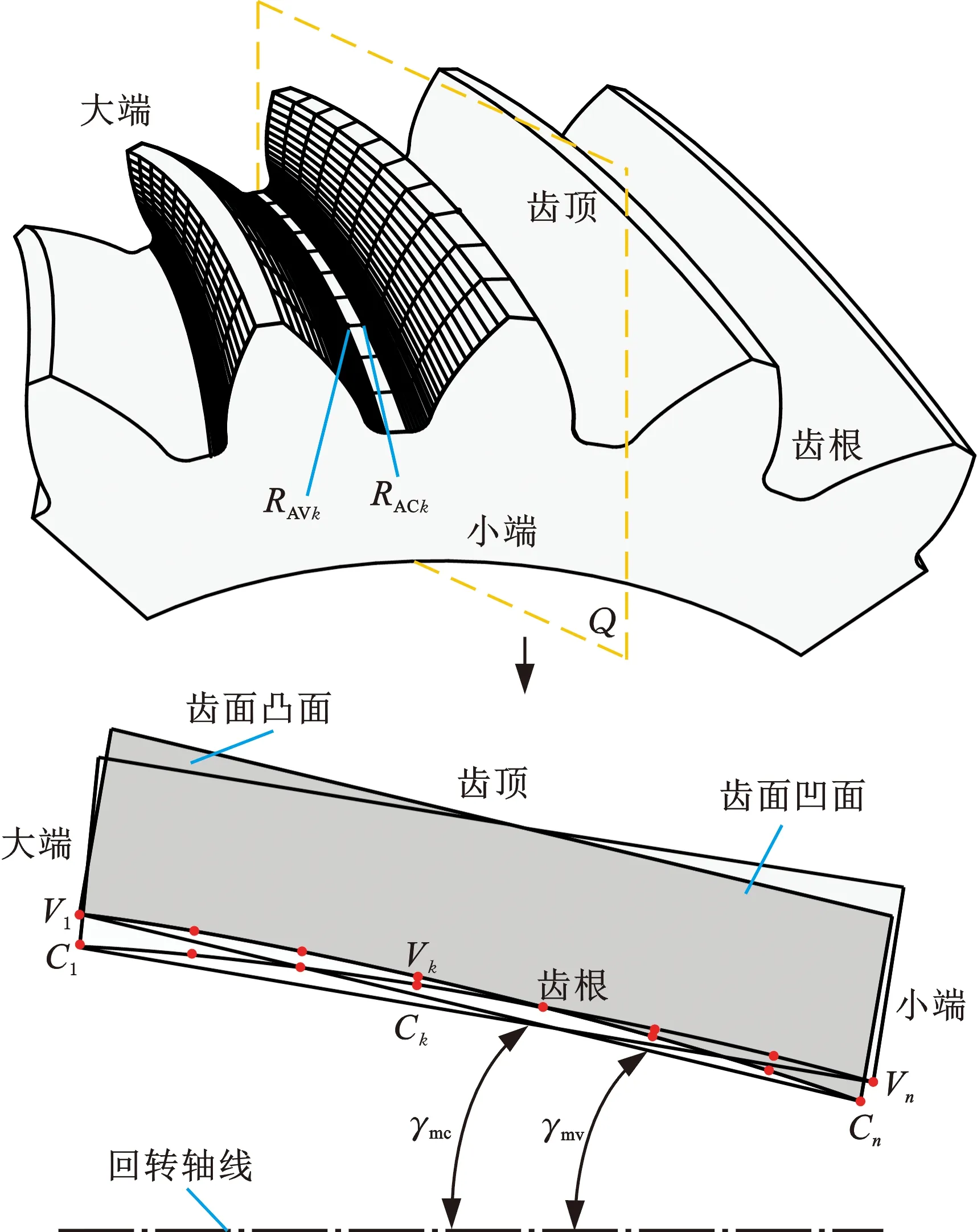
图8 轮齿根部错层修正方法Fig.8 Corrected approach of root parts of gear flank
消除齿轮根部过渡区台阶的方法为通过迭代使齿轮凹凸面机床根锥角逼近齿轮根锥角。基于此,提出针对小交错角准双曲面齿轮啮合特性控制的技术路线,如图9所示。
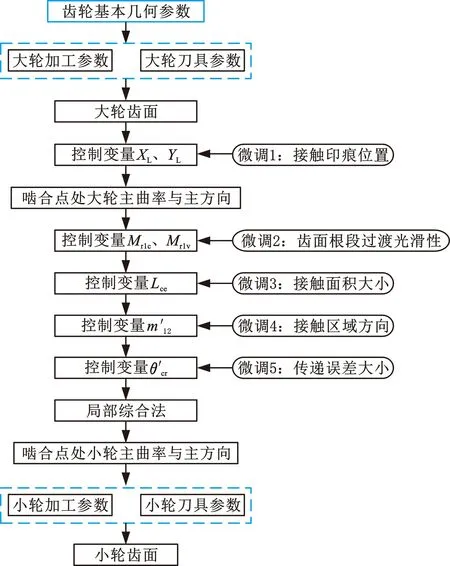
图9 小交错角准双曲面齿轮啮合特性控制技术路线Fig.9 Technology roadmap of mesh behavior controlling methodology of hypoid gear in low crossed shaft angle
基于齿轮基本参数可计算大轮加工参数与刀具参数,求解啮合方程可得到大轮齿面。设置循环变量1(理论啮合点与节圆锥参考点的距离),基于该啮合点的位置,可计算齿面在该点的主曲率和主方向。设置循环变量2(凹凸面机床根锥角)、循环变量3(接触椭圆长轴长度)、循环变量4(接触迹线与齿面第一主方向的夹角)、循环变量5(传动误差1阶导数预设值),通过上述参变量的预设值可求解出小轮加工参数与刀具参数,进而求得小轮齿面精确点集[4]。
3 基于轮齿接触分析的齿面啮合特性研究
基于上述计算流程,可推导出小交错角准双曲面齿轮副所有几何参数与加工参数。由于该齿轮工况特殊性与齿面几何形貌复杂性,上述啮合特性预置方法并未得到有效验证,外载荷对齿面啮合特性的影响也尚不清楚,因此,需建立啮合模型并对该齿轮副进行啮合分析。
3.1 齿轮副啮合模型
基于上述小交错角准双曲面齿轮副几何设计与啮合特性控制方法,计算得到小交错角准双曲面齿轮副基本几何参数;通过预设啮合特性参数,可得到大轮机床、小轮机床的加工参数,如表1~表4所示。
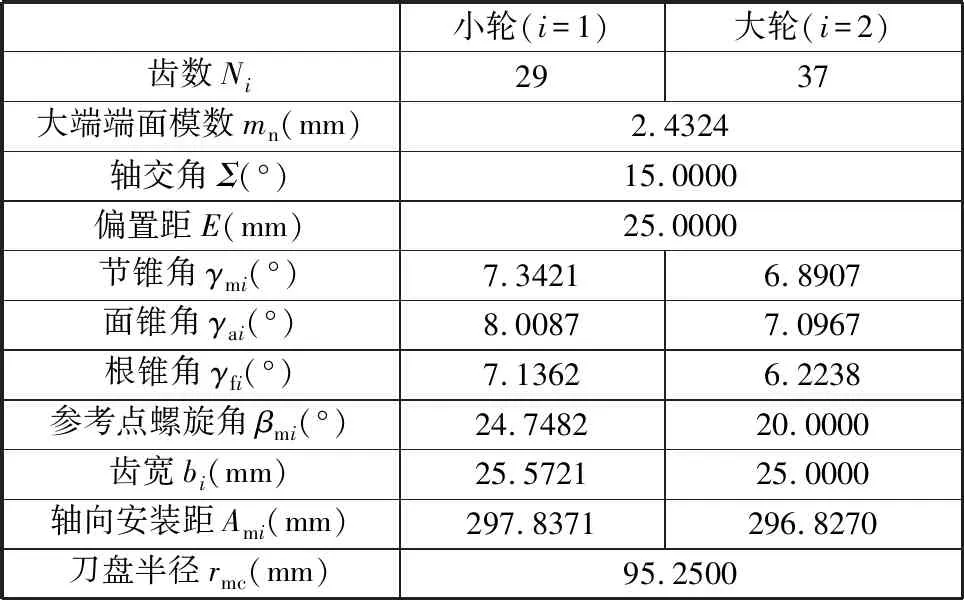
表1 小交错角准双曲面齿轮副基本几何设计参数

表2 小交错角准双曲面齿轮副预设啮合特性参数
基于齿轮基本设计参数、机床加工参数以及齿面创成原理,建立小交错角准双曲面齿轮副啮合模型。如图10所示,Am1、Am2分别为小轮与大轮的安装距离。轮齿根部平滑无错层、无根切,齿顶部分无变尖;齿轮副按照装配设计参数进行装配,可正确啮合,从而验证了上述设计优化方法的正确性。

表3 小交错角准双曲面齿轮副大轮机床加工参数
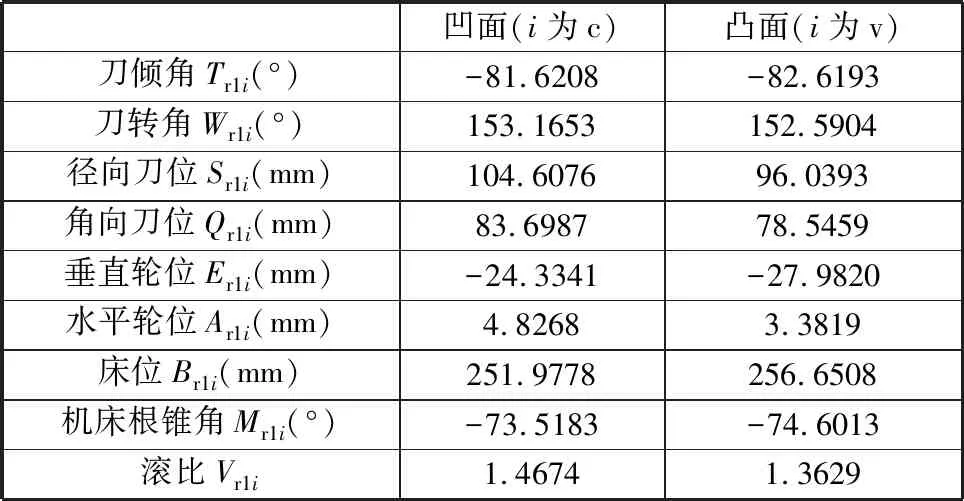
表4 小交错角准双曲面齿轮副小轮机床加工参数
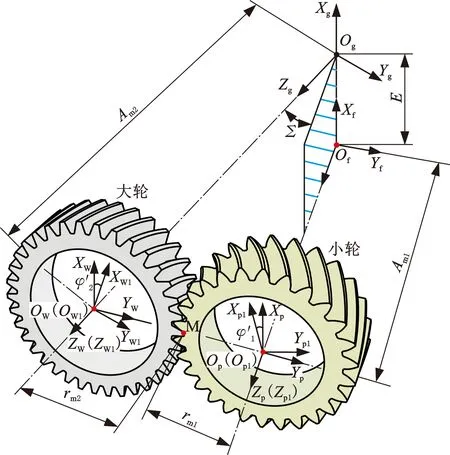
图10 小交错角准双曲面齿轮啮合模型Fig.10 Mathematical model of hypoid gear in low crossed shaft angel
由于小交错角准双曲面齿轮齿面几何形貌的特殊性,传统齿面接触分析方法在求解齿面非线性方程时,收敛性很差、效率低且对初值选取要求较高。
本文采用GALINA等[6]提出的齿面离散分析方法,将小轮、大轮的齿面离散成m×n的点集,并在全局坐标系Sf中旋转,两点间距小于6.35 μm(丹红颗粒直径)时即默认两齿面相接触时,两齿轮齿面离散点间距为
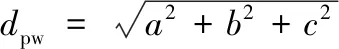
(21)
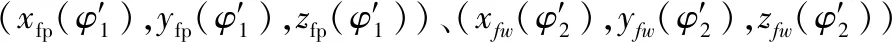
将两转角设为循环变量,遍历整个啮合过程,可得到齿轮副啮合过程中所有接触点。
图11所示为齿面接触分析的结果,可以看出,接触印痕在齿面中部,接触椭圆长轴与预设值(8 mm)一致;接触迹线与第一主方向交角与预设值(80°)一致;传动误差峰峰值与预设值(-15.0″)接近。从理论分析角度验证了上述方法的可行性与正确性。
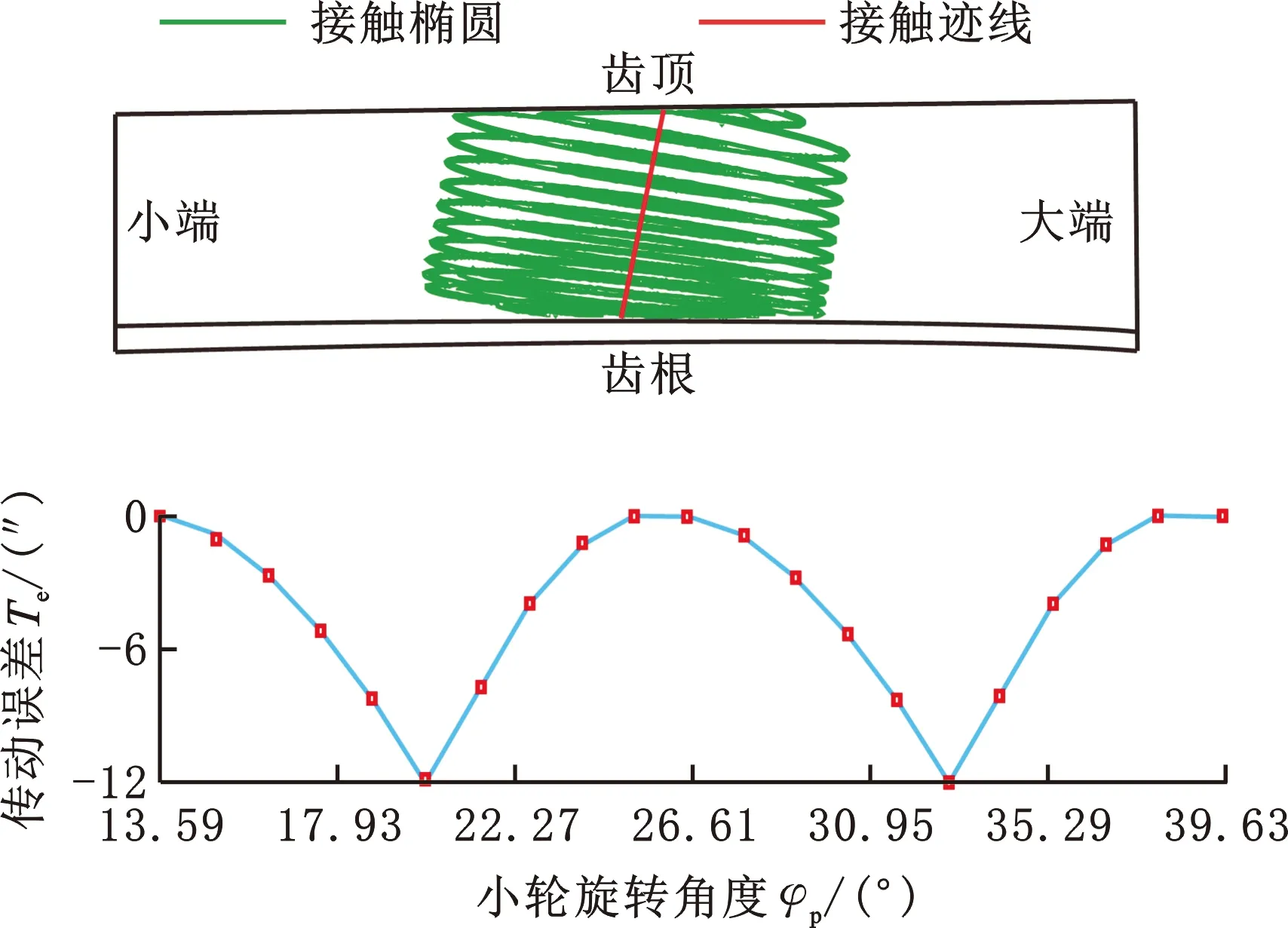
图11 基于齿面接触分析的齿轮啮合印痕与传动误差Fig.11 Contact pattern and transmission error based on the tooth contact analysis
小交错角准双曲面齿轮副有限元分析模型如图12所示。齿轮设置材料属性为各项同性(isotropic),泊松比为0.3,弹性模量为209 GPa。齿面接触约束与边界约束,如图12a所示,小轮作为主动轮施加转角,大轮作为从动轮施加力矩(方向与大轮转动方向相反)。小轮凹面与大轮凸面设置接触约束(interaction)。齿轮副网格划分如12b所示,采用六面体网格C3D8R,齿轮副接触面以及相邻齿顶齿根部分的网格密集,工作面布种100×30个,其余部分为提高运算效率,以收敛无畸变为原则,尽可能减少网格;该模型小轮有126 323个网格,大轮有134 791个网格。
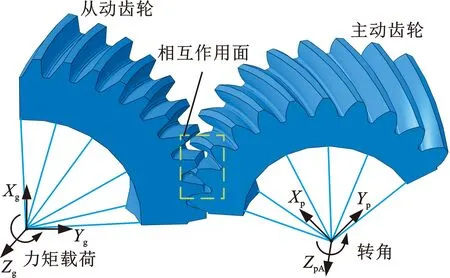
(a)齿轮副接触与边界约束
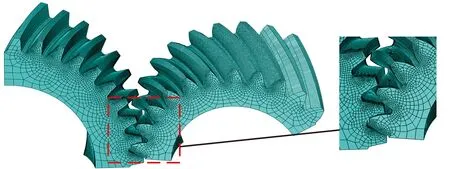
(b)齿轮副网格模型图12 小交错角准双曲面齿轮有限元分析模型Fig.12 Finite element model of hypoid gear in low crossed shaft angle
3.2 外载荷对齿轮啮合特性的影响
图13所示为不同扭矩下,基于齿面承载分析的小轮齿面接触印痕。随着工作扭矩的增大,接触椭圆长轴长度逐渐增大,齿面法向应力不断增大,接触区域占齿面百分比不断增大,但接触印痕齿面位置与接触迹线方向没有改变,验证了上述预置啮合特性方法的正确性。
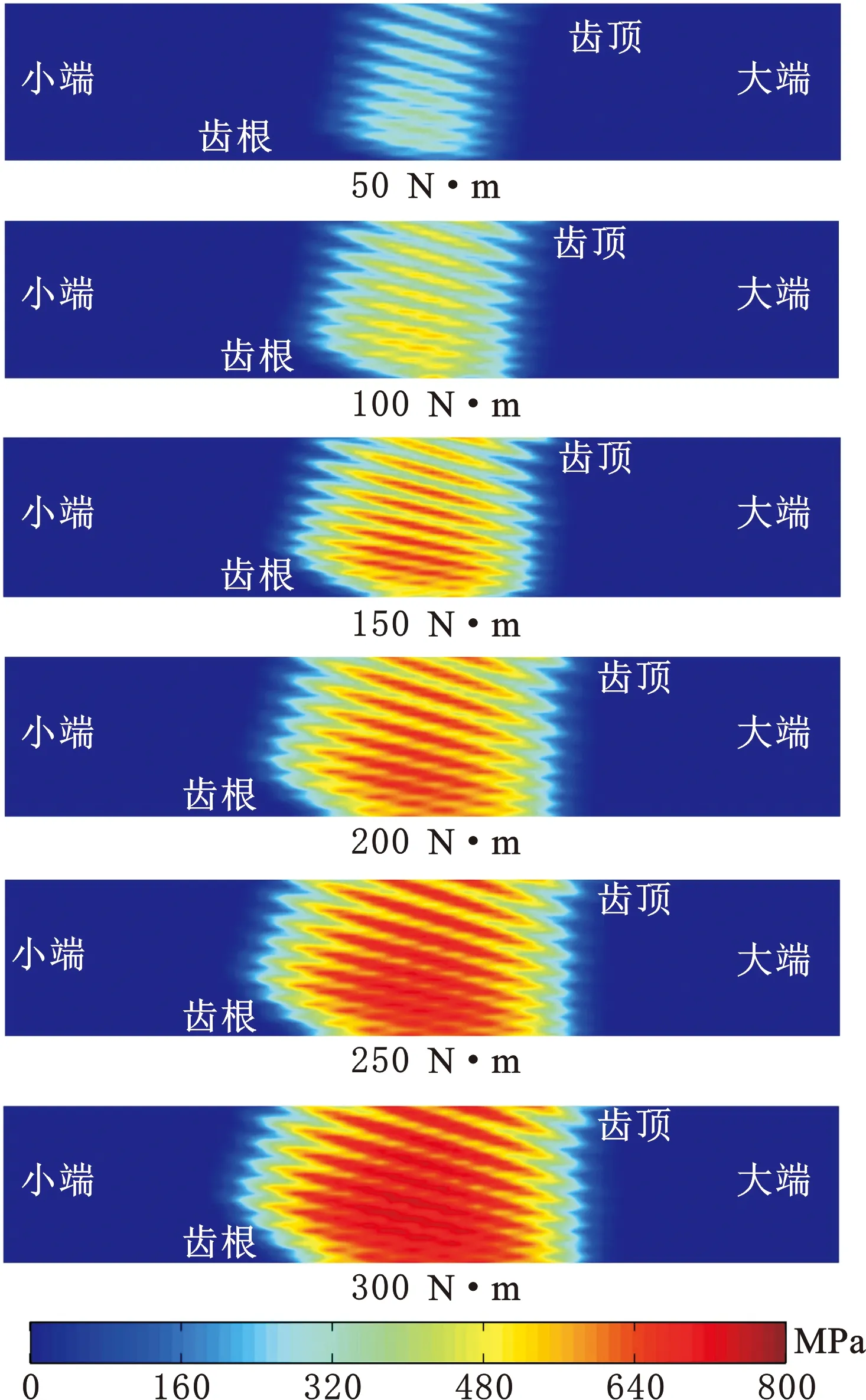
图13 基于齿面承载分析的齿轮啮合印痕Fig.13 Contact pattern based on the loaded tooth contact analysis
传动误差随载荷T变化的规律如图14a所示,传动误差曲线光滑,无明显尖点;载荷增大时,轮齿形变也逐渐增大,传动误差逐渐增大,传动误差曲线向下移动。传动误差峰峰值随载荷变化的拟合曲线如图14b、图14c所示,传动误差峰峰值随着载荷的增大先减小、后增大。
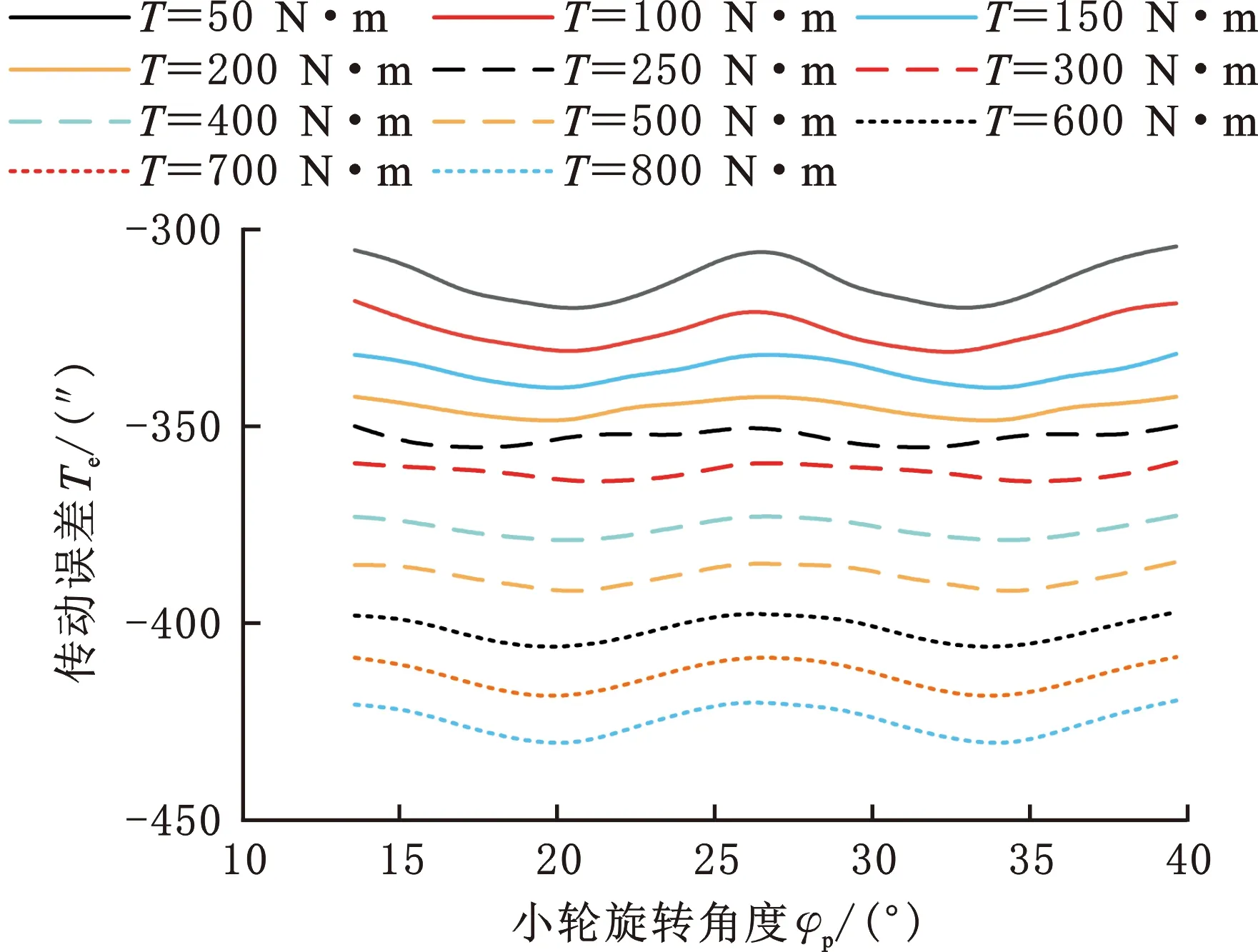
(a)不同载荷下传动误差
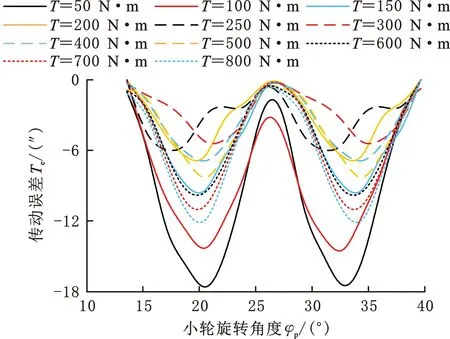
(b)不同载荷下去除平均值的传动误差
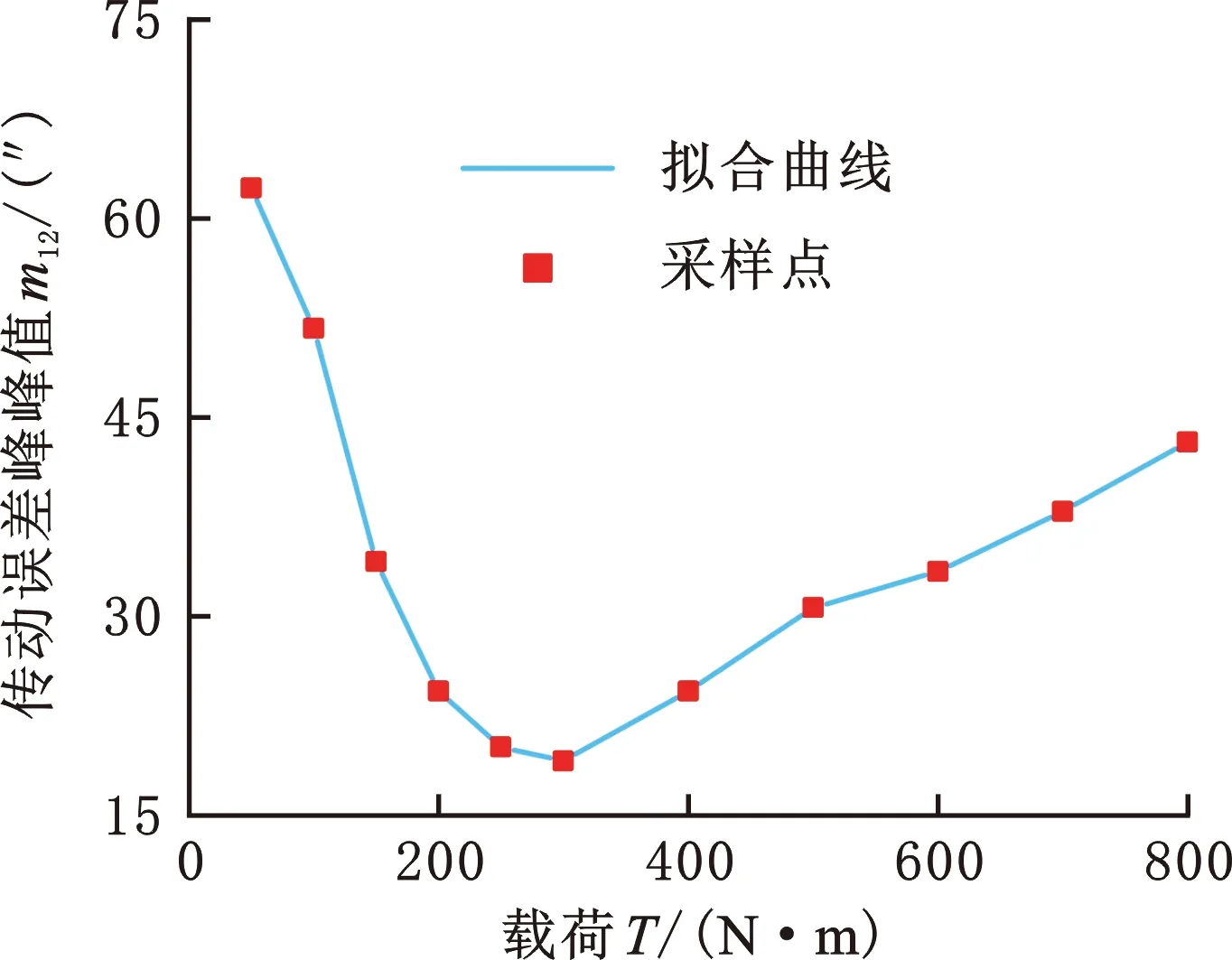
(c)不同载荷下传动误差峰峰值图14 基于齿面承载分析的齿轮传动误差Fig.14 Transmission error based on loaded tooth contact analysis
3.3 外载荷对齿面接触应力与齿根弯曲应力的影响
图15所示为不同外载荷下,小交错角准双曲面齿轮副齿面齿根弯曲应力的变化。随着载荷增大,齿面弯曲应力逐渐增大;齿根弯曲应力随齿向方向呈现先增大后减小,且曲线形状随着载荷增加无明显变化,与啮合印痕变化(图13)一致。
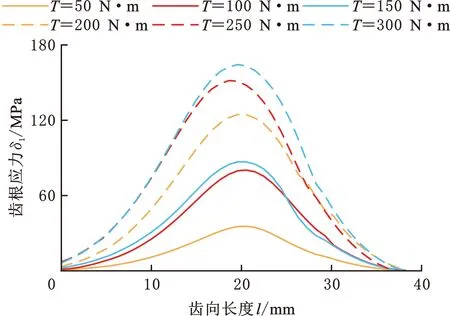
图15 外载荷对齿根弯曲应力的影响Fig.15 Influence of different loads on root bending stress
图16所示为小交错角准双曲面齿轮副齿面接触应力在不同外载荷下的变化。随着外载荷的增大,齿面接触应力增大,载荷超过100 N·m后,齿面在啮入与啮出时(齿顶、齿根处)产生边缘接触,导致齿面接触应力激增,影响啮合质量,具体如图中A和B区域所示。
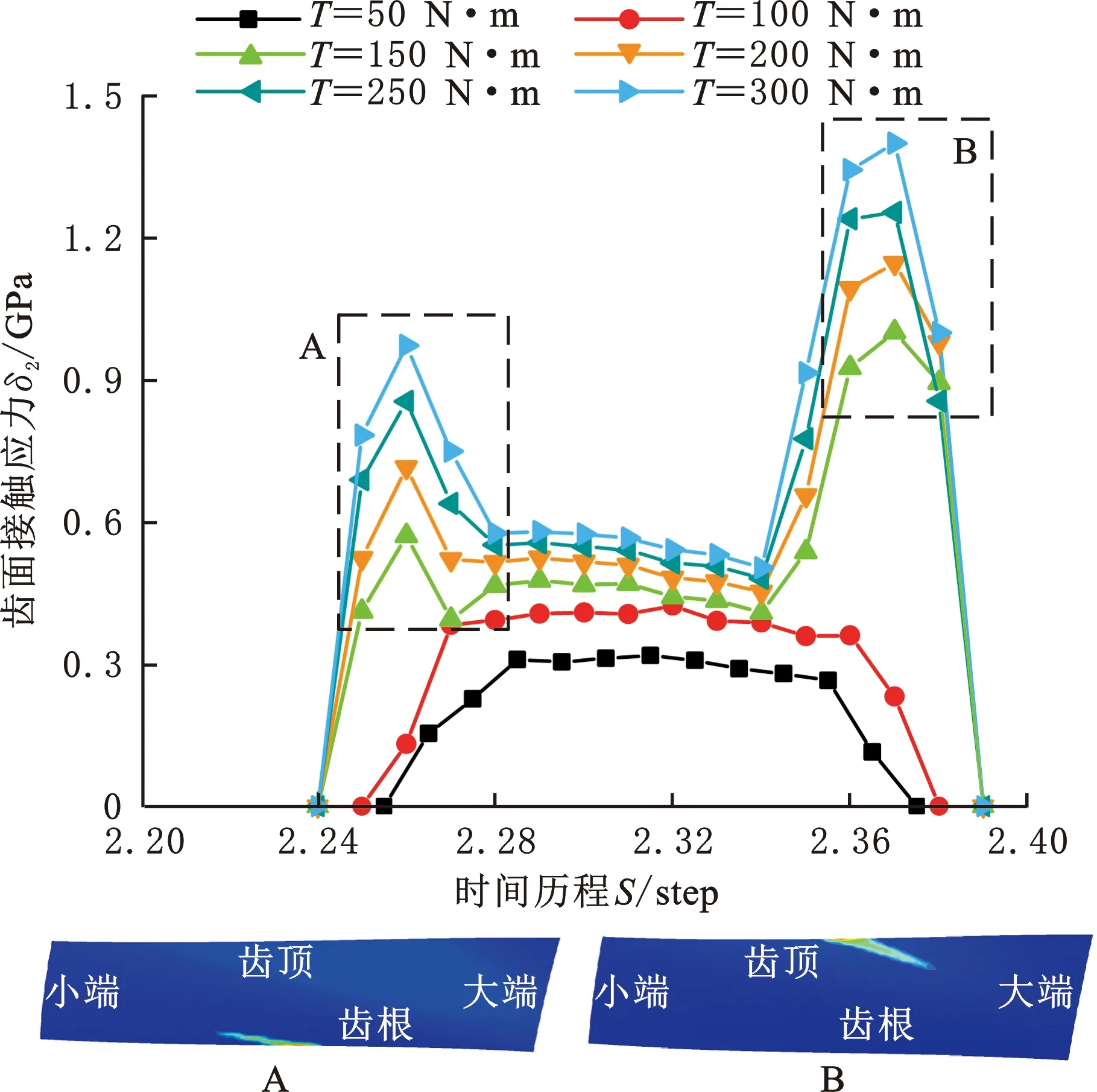
图16 外载荷对齿面接触应力的影响Fig.16 Influence of different loads on contact stress
4 小交错角齿轮传动原理样机
基于小交错角准双曲面齿轮副啮合模型,通过3D打印(打印精度0.05 mm)技术加工小交错角准双曲面齿轮副,如图17所示。

图17 基于3D打印技术的小交错角准双曲面齿轮副Fig.17 Hypoid gear in low crossed shaft angle based on 3D printer technology
交错角齿轮传动原理样机如图18所示,输入轴为小交错角准双曲面齿轮小轮回转轴,通过联轴器与电机相连接,输出轴为变厚齿轮小轮,输入轴、输出轴平行。两组齿轮副的小轮与各自大轮成15°交角,依靠分度盘控制,精度为0.02°。变厚齿轮副偏置距为60 mm,小轮、大轮的齿数分别为25与39,具体设计方法见文献[3-5]。

图18 小交错角齿轮传动原理样机详细结构图Fig.18 Structure chart of low crossed shaft angle transmission system prototype
小轮、大轮的齿廓与理论模型一致,按设计参数装配后,整个系统传动平稳。该原理样机验证了准双曲面齿轮在小交错角极端工况下平稳工作的能力,验证了针对小交错角工况的准双曲面齿轮几何参数与加工参数设计方法的正确性与可行性,说明了上述齿轮齿面模型的正确性。
5 结论
(1)基于空间单叶双曲面瞬时轴线和准双曲面齿轮啮合机理,推导了小交错角准双曲面齿轮空间三大几何关系、极限压力角、极限法曲率的表达式,提出了以大轮偏置角与节锥角为循环变量,偏置距与刀盘半径收敛为判定条件的技术路线。
(2)基于准双曲面齿轮齿面创成机理,提出了考虑齿面优化与啮合特性预置的小交错角准双曲面齿轮加工参数计算方法。基于该方法,建立了基于迭代凹凸齿面机床根锥角使齿面根部平滑过渡的齿轮加工参数求解技术路线,并建立了基于上述流程的几何参数齿轮副啮合模型。
(3)基于小交错角准双曲面齿轮啮合模型,通过齿面接触分析与齿面承载分析,探究了不同外载荷对啮合特性及齿面应力的影响。随着外载荷
的增大,齿轮啮合印痕、轮齿接触应力、弯曲应力逐渐增大;载荷过大会产生齿顶、齿根边缘接触,但接触印痕位置与接触迹线夹角没有明显变化;传动误差随着载荷的增大,逐渐增大;峰峰值随着载荷的增大,先减小后增大。上述结果验证了啮合特性预置方法的可行性与正确性。
(4)通过齿面点云建立了齿轮副实体模型,利用3D打印技术加工了与理论齿面一致的齿面;设计了小交错角准双曲面齿轮副与变厚齿轮副相组合的原理样机,样机验证了针对小交错角准双曲面齿轮几何设计、加工参数计算、齿轮副建模方法的正确性。

