基于神经-肌肉架构的仿生并联躯干柔顺控制

朱雅光 朱建伟 李茹月 宋志鹏

长安大学道路施工技术与装备教育部重点实验室，西安，710064

0 引言

在过去十年间，仿生机器人在机械结构、控制方法、能耗特性、稳定性与协调性等方面的研究都有了长足的进展。现有的仿生机器人大都可在复杂地形上实现步态切换和稳定运动，但很少有机器人具有动物般的灵活性、柔顺性和快速响应性。生物学研究表明，生物躯干的弯曲和伸展可以增大动物奔跑的步幅[1]，储存和释放能量，抵抗外界冲击，减少高速运动步态时的能耗[2]。SCHILLING[3]发现老鼠和兔子通过调整躯干姿态来改变四肢着地的角度和位置，使整体质心轨迹始终保持平稳，躯干的主动作用提高了鼠和兔的运动稳定性。DENG等[4]、BERTRAM等[5]通过观察猎豹的运动模式发现，猎豹在高速奔跑时，它的躯干可随四肢的周期性运动有节奏地伸展和弯曲以增大步幅。生物躯干的灵活性和协调性有益于提高动物运动速度。为使仿生机器人具有动物一般优良的运动特性，许多学者和研究人员对仿生躯干做了大量研究。CheetahRobot的运动速度可达45 km/h，其极限运动性能甚至可以和一些动物相媲美[6-8]。

鉴于此，本文将六自由度并联平台作为仿生躯干，并对仿生躯干的柔顺控制进行研究。这种并联机构与动物躯干构型[9]类似，具有多个自由度，还具有类似猎豹、马等动物躯干的灵活性、柔顺性和快速响应性。到目前为止，对并联机构控制方法的研究大多都集中在基于动力学模型的控制[10]、冗余驱动控制[11-12]和轨迹跟踪控制[13]。躯干实现柔性的方法有弹性元件被动柔顺[14-15]、主动驱动柔顺控制[16-17]。刚度可调的被动柔性躯干稳定、能效高，但速度变化或其他特殊情况时的刚度调节有困难。刚度调节不合适时，容易出现失稳现象。主动驱动型躯干可有效提高仿生机器人的运动速度，但由于躯干输出是预先规划好的，缺乏与外界环境的交互，因此不具备动物躯干的优点。主动柔顺控制可使仿生躯干模拟动物躯干、实现柔顺运动，因此，本文对仿生并联躯干的主动驱动柔顺控制进行研究。

本文针对仿生并联躯干[9]提出了一种基于神经肌肉控制架构的柔顺控制方法，将6个σ-Hopf非线性振荡器[18-19]作为中枢模式发生器，进而构成仿生并联躯干的神经控制网络。中枢模式发生器产生的节律信号经处理后，发送到电机从而控制6条支链协调运动。受动物肌肉模型[20]启发，本文在并联躯干输出关节的两侧构建了一对虚拟的主动肌-拮抗肌模型，在确保并联躯干快速响应的前提下，通过调节参数获得肌肉模型的刚度系数和阻尼系数。仿生肌肉控制方法将外负载转换为关节转角来驱动仿生躯干进行顺应运动。初始位姿给定时，并联平台在外力作用下的位姿变化可用来验证该方法有效性。

1 仿生并联躯干概述

1.1 结构概述

如图1所示，并联躯干由动平台、静平台和6个完全相同的支链构成。静平台和动平台通过支链连接，每条支链由2个球铰、1个连杆、1个摇杆、1个力传感器、1个电机组成。电机的额定电压为24 V，转矩常数为11.8 mN·m/A，转速常数为809 (r/min)/V，内置23∶1的行星减速器。6个直流伺服电机分成3组均布在静平台上，每组间隔120°。电机与静平面通过夹角为60°的连接件连接。支链中串联的力传感器实时采集连杆的受力信息。动平台中心安装有检测动平台姿态的传感器。并联躯干的运动是通过摇杆绕电机输出轴旋转带动连杆运动实现的。

图1 仿生并联躯干的机械结构Fig.1 Mechanical structure of bionic parallel torso

1.2 运动学分析

仿生并联躯干的几何构型如图2所示，6台电机分为3组(1-6、2-3、4-5)，静平台、动平台的坐标系分别用{B}和{P}表示，坐标系的原点分别为OB和OP，{B}和{P}的Z轴垂直于平台。SP，i和SB，i分别为连杆两端的2个球铰中心，RB，i为电机轴线与摇杆中心线的交点，下标i表示第i条链，其他的结构参数如表1所示。动平台绕X轴的翻滚角为ψ，绕Y轴的俯仰角为θ，绕Z轴的偏航角为φ。

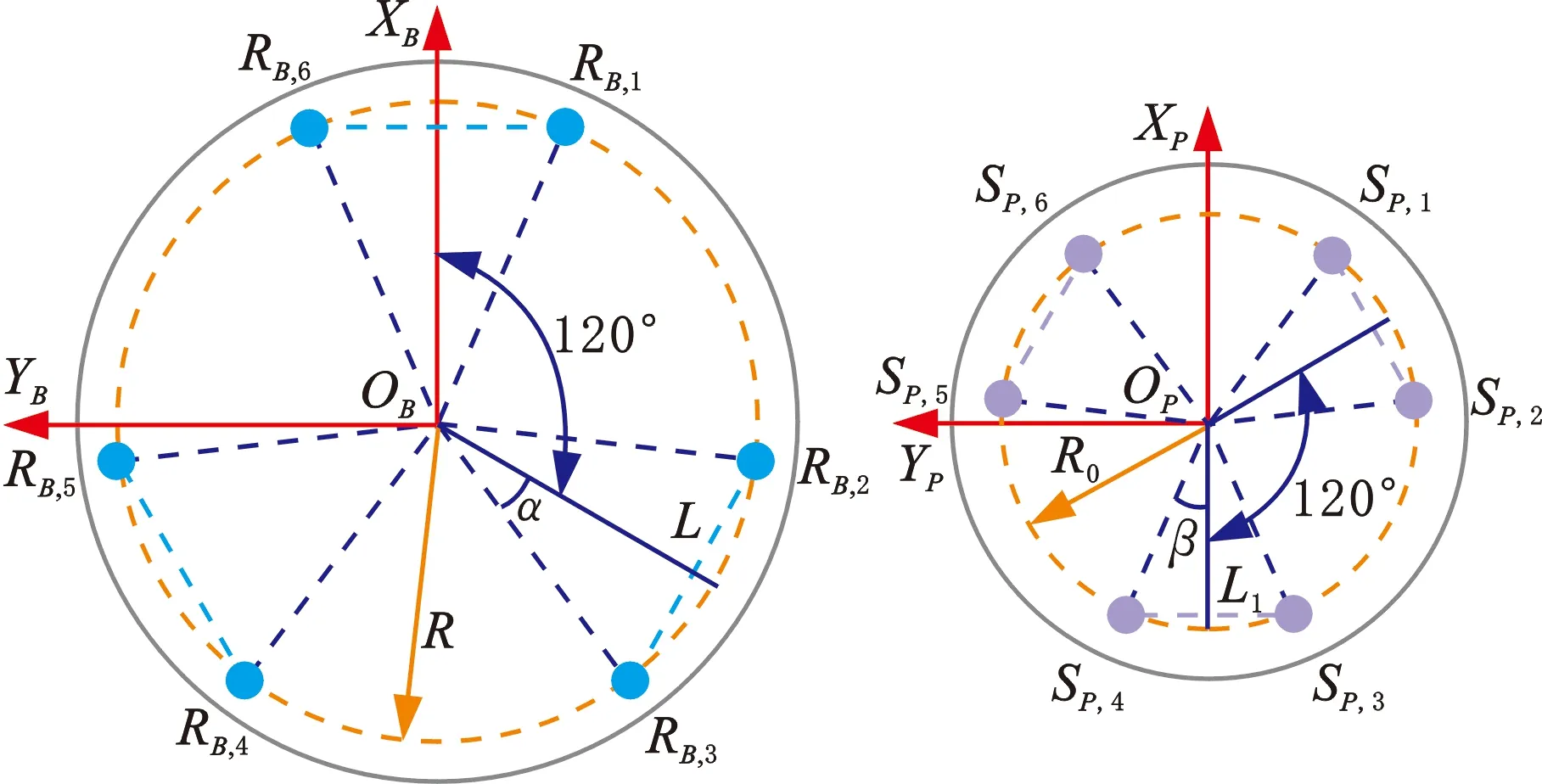
(a)静平台俯视图 (b)动平台俯视图

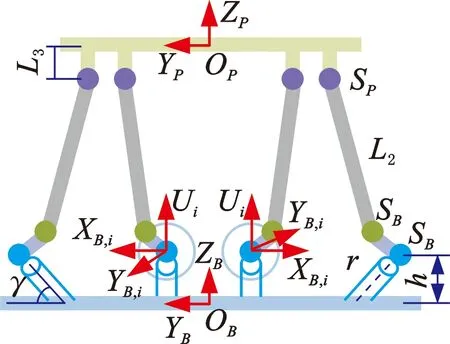
(c)仿生并联躯干侧视图图2 仿生并联躯干的几何构型Fig.2 Geometrical configuration of bionic parallel

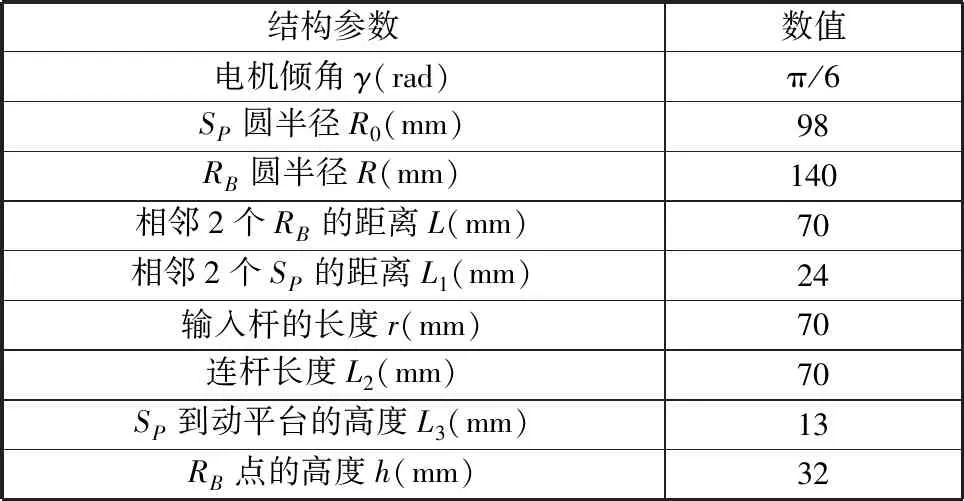
表1 结构参数

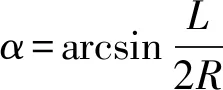
如果已知动平台在{B}坐标系下的位置(x，y，z)和姿态(φ，θ，ψ)，那么{B}坐标系下的向量OBSP，i为

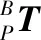
对于{B}坐标系，电机输出轴轴线的方向向量Ui=(hcosζ/tanγ，hsinζ/tanγ，h)，其中，ζ为电机在静平台平面的投影与XB轴的夹角，ζ∈{0，-2π/3，-2π/3，-4π/3，-4π/3，0}。在电机输出轴与摇杆轴线的交点建立新的坐标系，该坐标系X向的方向向量为

Y轴方向的方向向量为

Z轴方向的方向向量为

ZB=(0，0，1)

摇杆矢量RB，iSB，i=r(XB，icosθi+YB，isinθi)，支链矢量RB，iSP，i=OBSP，i-OBRB，i，连杆矢量SB，iSP，i为支链与摇杆的矢量差即SB，iSP，i=RB，iSP，i-RB，iSB，i。根据余弦定理可得点SP，i到SB，i的距离：

|SB，iSP，i|=L2=

(2)

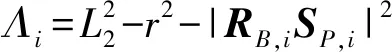
Λi+2RB，iSP，i·r(XB，icosθi+YB，isinθi)=0

(3)

将χ=tan(θi/2)代入式(3)可得

χ2(Λi-2rXB，i·SB，iSP，i)+χ(4rYB，i·SB，iSP，i)+

2rXB，i·SB，iSP，i+Λi=0

(4)

式(4)为χ的一元二次方程，通过解算式(4)，得到电机i的转角θi=2arctanχ。

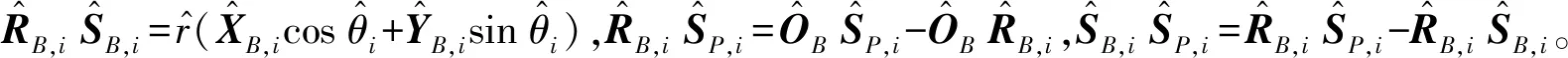
(5)

(6)

最后，应用牛顿-拉夫逊求解方法[21]，求解出动平台的位置和姿态。

1.3 运动空间

分析并联机构的运动空间得到并联机构的俯仰角θ∈[-12°，18°]、翻滚角ψ∈[-12°，12°]、偏航角φ∈[-40°，40°]。并联机构的可达姿态与马和猫躯干弯曲、翻滚、扭转可达的角度相近，因此可用于模仿躯干的弯曲、侧转、扭转。同时，并联机构的运动空间比马在3种步态(慢跑、小跑、行走)下运动时躯干的运动空间都要大。这说明本文设计的仿生并联机构的运动空间可以与马和猫在任意运动模式下躯干的运动空间相媲美。

2 控制架构

整个仿生并联躯干的控制架构如图3所示。先生成躯干的运动轨迹，由运动轨迹决定的位姿(xd，yd，zd，φd，θd，ψd)经逆运动学运算可求解出电机i(i=1，2，…，6)的关节转角qi。将qi作为角度指令发送给电机，动平台即可运动到期望的位姿状态。仅由逆运动学解算的电机角度控制的躯干不具备柔顺性，因为躯干关节会保持在期望位置且不因外负载干扰而改变。躯干受到外力冲击时，构件极易损坏。为避免冲击损坏机构，引入顺应性姿态控制模块使并联躯干在外力作用下产生柔顺运动。肌肉控制模型(muscle control model，MCM)根据力传感器反馈的力Fs可计算得到偏置角qvj(j=1，2，…，6)。逆运动学所求关节角与肌肉控制模型求解的肌肉缓冲偏置角之和为电机实际的转角，即并联躯干在外力作用下达到轨迹期望的位姿后，躯干关节还需转过偏置角qvj来模拟肌肉伸缩，使支链具备一定的缓冲性能。因此，将q=qi+qvj作为电机的最终输出角度。下面介绍图3中每个模块的具体功能。

2.1 神经运动控制网络模块

为实现类哺乳动物的仿生运动轨迹，构建图4所示的神经运动控制网络，通过反向控制策略[18，22]实现类动物的节律性运动行为。σ-Hopf非线性振荡器构成中枢模式发生器(CPG)单元；6个CPG耦合形成的神经运动控制网络生成6个关节的节律信号，节律信号经信号耦合模块后用于轨迹规划。位姿轨迹根据动物行为设计，期望关节转角由逆运动学计算得到，最终用来驱动电机转动。耦合σ-Hopf非线性振荡器的数学表达式为

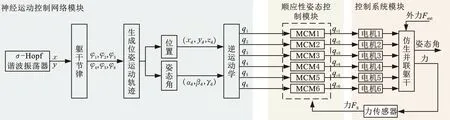
图3 仿生并联躯干控制架构Fig.3 Bionic parallel torso control architecture

(7)

(8)

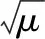
参数η决定了上升阶段和下降阶段之间的转换速度，由式(7)、式(8)可以发现T和ρ是不相关的，这意味着运动周期不会受到占空比变化的影响。

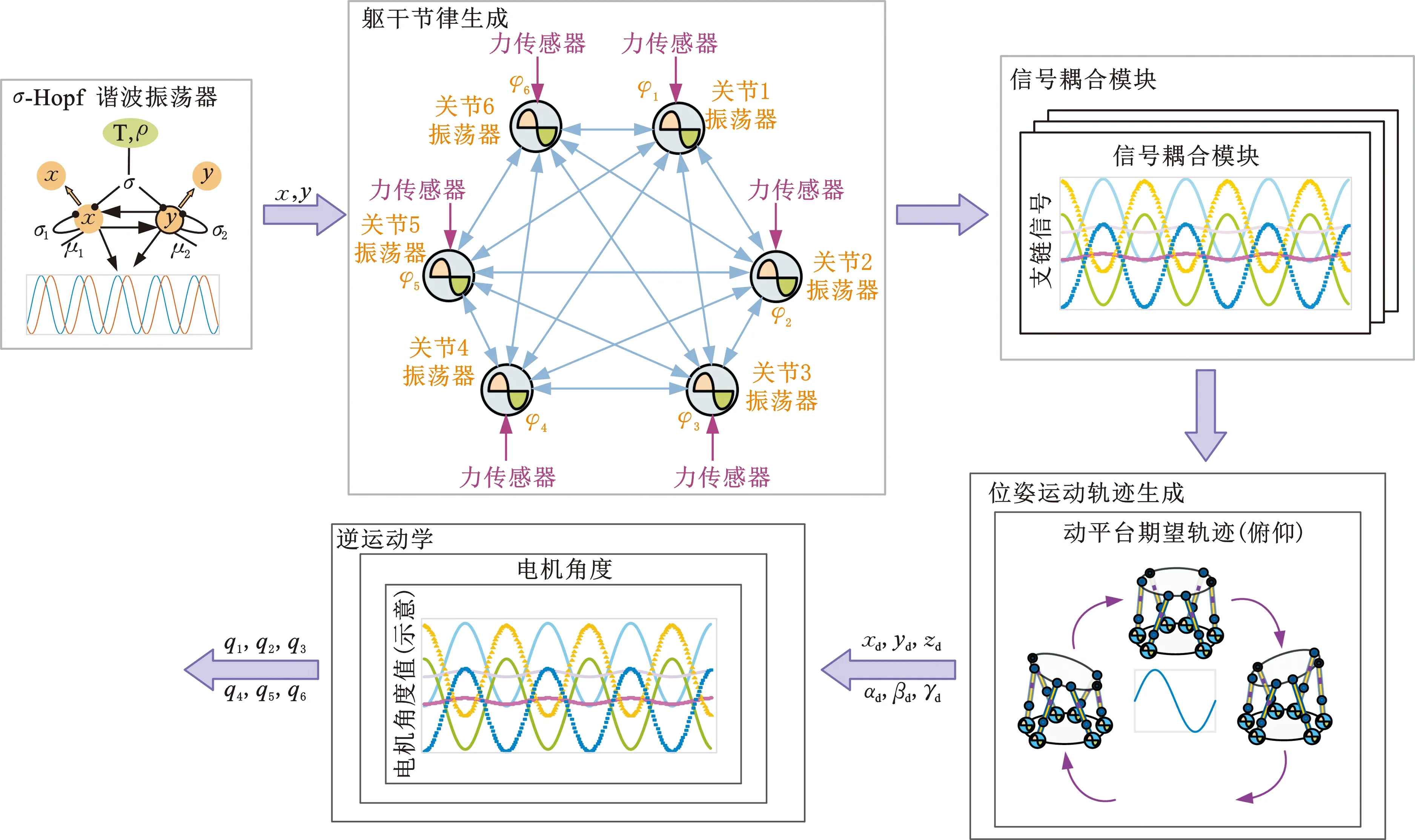
图4 并联躯干的神经运动控制网络Fig.4 Neural motor control network of parallel trunk

2.2 顺应性肌肉控制模块

MCM在顺应性姿态控制中起重要作用。单支链的虚拟肌肉模型布置如图5所示。定义输入杆转动所在平面为投影面A，将输入杆绕RB,i点旋转一周形成的圆等效为1个虚拟转动关节，然后假想虚拟转动关节两端有虚拟的拮抗肌肉M1和M2(产生的虚拟肌肉力分别为FT1和FT2)拉动关节转动。M1和M2分别由平行成分(parallel elements，PE)和收缩成分(contractile elements，CE)组成，PE产生被动力FP，CE产生主动力FC。通过肌肉刚度阻尼系统对每个PE进行建模，由PE产生的被动力为

FP=K(lP-l0)+D(vP-v0)

(9)

其中，K、D分别为肌肉的刚度系数和阻尼系数，为简化被动力的求解过程，假定刚度系数和阻尼系数相等，即K1=K2=K，D1=D2=D；lP、l0分别为PE的长度和初始长度；vP、v0分别为PE的速度和初始速度。

图5 肌肉控制模型Fig.5 Muscle control model

主动力由激活系数α和虚拟肌肉长度与速度的关系表达函数F(lC，vC)共同决定[23]，其中，lC、vC分别为CE的长度和速度，那么CE产生的主动力为

FC=αF(lC，vC)

(10)

FT1、FT2均为被动力和主动力之和，即

FT1=K(lP1-l0)+DvP1+α1F(lC1，vC1)

(11)

FT2=K(lP2-l0)+DvP2+α2F(lC2，vC2)

(12)

如图5所示，支链中的连杆可以看作是一根任意截面受力大小相等的二力杆。转动关节在外力Fext的作用下有顺时针转动的趋势，因此，肌肉控制模型中的虚拟肌肉M1有阻止转动关节转动即伸长的趋势，产生力FT1；虚拟肌肉M2与M1相反，有收缩的趋势，产生力FT2。FT1和FT2绕转动关节圆心P的力矩方向分别为逆时针和顺时针。为了方便计算Fext绕P点的力矩，定义λi=ϑi×Ui为连杆力Fext与其投影所在平面的法向量，其中，ϑi为连杆受力方向的单位向量。定义ni=Ui×λi为Fext在平面A中的投影向量。Fext和投影面A的夹角ζi、摇杆与Fext在平面A上的投影间的夹角δi分别为

(13)

Fext对转动中心P的力矩为

τi(Fext)=Fext，ircosζi|sinδi|

(14)

式中，Fext，i为第i条连杆受力。

FT1和FT2的绕转动中心P的转矩分别为

τi(FT1)=-FT1r1

(15)

τi(FT2)=FT2r1

(16)

式中，r1为输入杆的半径。

(17)

将式(14)～式(16)代入式(17)，可得

(18)

M1和M2是2块完全相同的虚拟肌肉，一个在拉伸，表现为伸肌，另一个在缩短，表现为屈肌。我们假设每个虚拟肌肉中PE和CE的长度都为虚拟肌肉的长度，即L1=lP1=lC1，L2=lP2=lC2；M1和M2的伸长量和缩短量相等，即ΔL1=-ΔL2。假定ΔL和关节转动角度θ的关系为

ΔL1=lP1-l0=θr=-ΔL2=-(lP2-l0)

(19)

虚拟肌肉的伸长和收缩速度为

(20)

设定PE的初始速度vP1=vP2=0，将式(19)、式(20)代入式(18)，得到

(21)

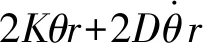
(22)

3 仿真分析

稳定柔顺的仿生躯干需在受到外界干扰(沿坐标轴的作用力和绕坐标轴的扭矩)时快速达到稳定状态且无超调和大幅波动。仿生躯干在外力作用下的姿态和关节转角可用来判断是否能实现快速柔顺的姿态控制。对整个仿生并联躯干柔顺特性的调节主要通过调整控制器参数来实现，比如式(22)中的肌肉刚度K和肌肉阻尼D。

3.1 肌肉刚度系数K和肌肉阻尼系数D

为明确各参数对系统特性的影响，先对肌肉控制数学模型(式(22))中的参数进行分析，对比不同参数下的仿生并联躯干的快速响应性和柔顺性，选择最优的K和D。仿真采用的控制架构与图3所示一致。结构参数如表1所示，初始位姿设定为(x，y，z，φ，θ，γ)=(0 m，0 m，0.27 m，0°，0°，0°)。

在D=5 N·s/m不变的情况下，增大K，动平台的高度减小，如图6所示。K=500 N/m时，动平台高度变化量为0.86 mm；K=700 N/m时，动平台高度降低了0.62 mm；K=1000 N/m时，动平台降低了0.44 mm。K过大时，动平台的高度几乎不会有任何变化，这与无肌肉控制模型的并联躯干相似，即动平台的高度为初始高度，不具备柔顺控制功能。K太小会使整个并联躯干柔性太大，如图6中的蓝色虚线。并联躯干还未受到负载(仅存在重力作用)作用时，动平台的高度下降很大，这种现象对并联躯干的负载性能有影响。考虑到K=700 N/m时动平台的高度变化量远小于竖直方向可达范围的最大值60 mm，故本文初步选用700 N/m作为后续仿真和实验的肌肉刚度系数。

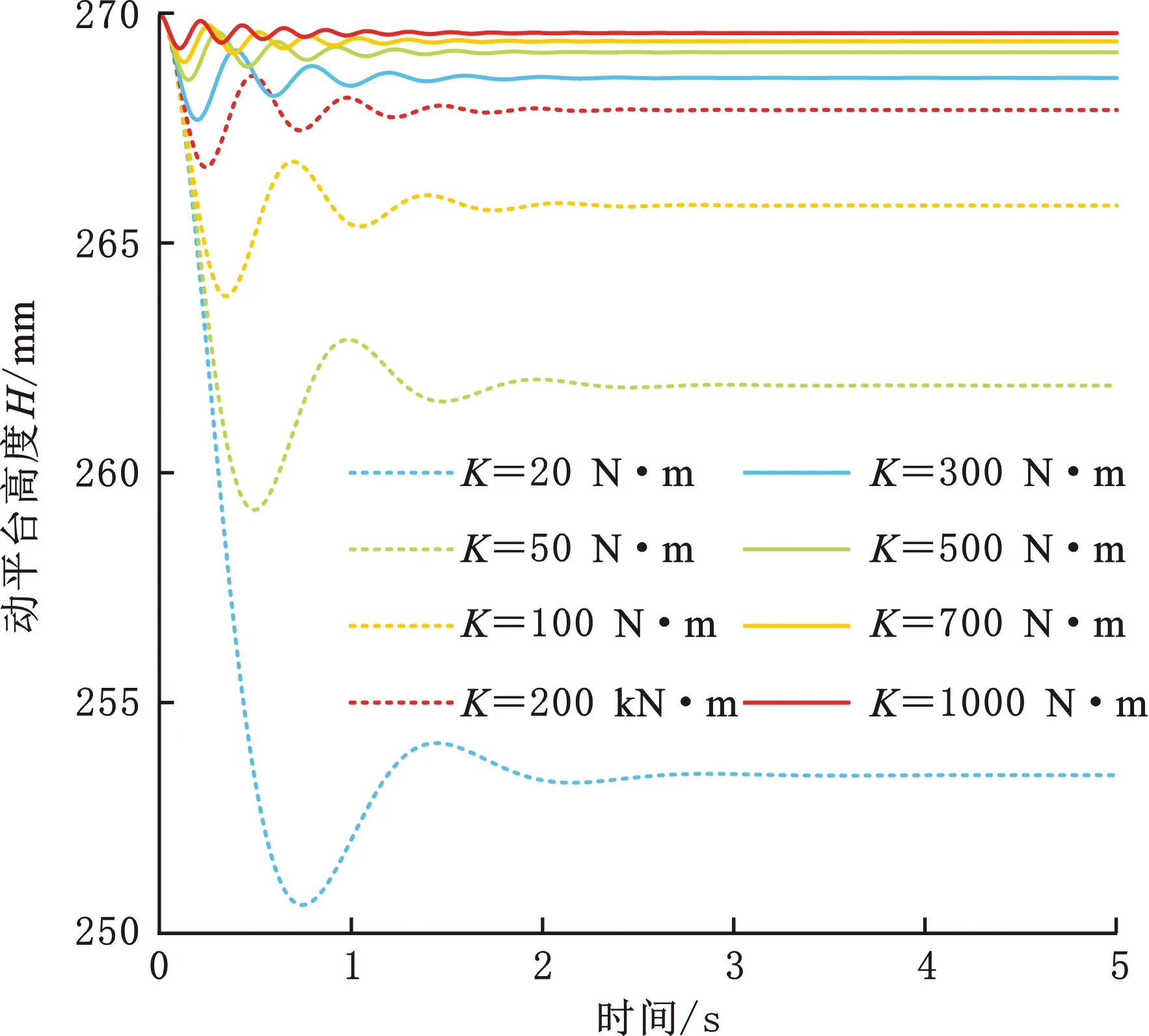
图6 K变化时动平台的高度变化(D=5 N·s/m)Fig.6 The height variation of moving platform when K varies(D=5 N·s/m)

初步确定肌肉刚度后，调整肌肉阻尼D，以便获得较短的动平台响应时间。变化的D并不影响稳态值，而仅影响动平台的响应速度和达到稳态的时间。增大D可以加快响应速度，但D增加到一定值后，达到稳定的时间会延长；D越小时，动平台高度曲线会有超调并伴随着小幅振荡，且响应变慢，稳态时间变长。如图7所示，K=700 N/m时，40 N·s/m、50 N·s/m、60 N·s/m对应的响应时间t分别为0.49 s、0.33 s和0.58 s。K=700 N/m，D=50 N·s/m时，动平台的响应最快，故后续仿真和实验的肌肉阻尼系数确定为50 N·s/m。

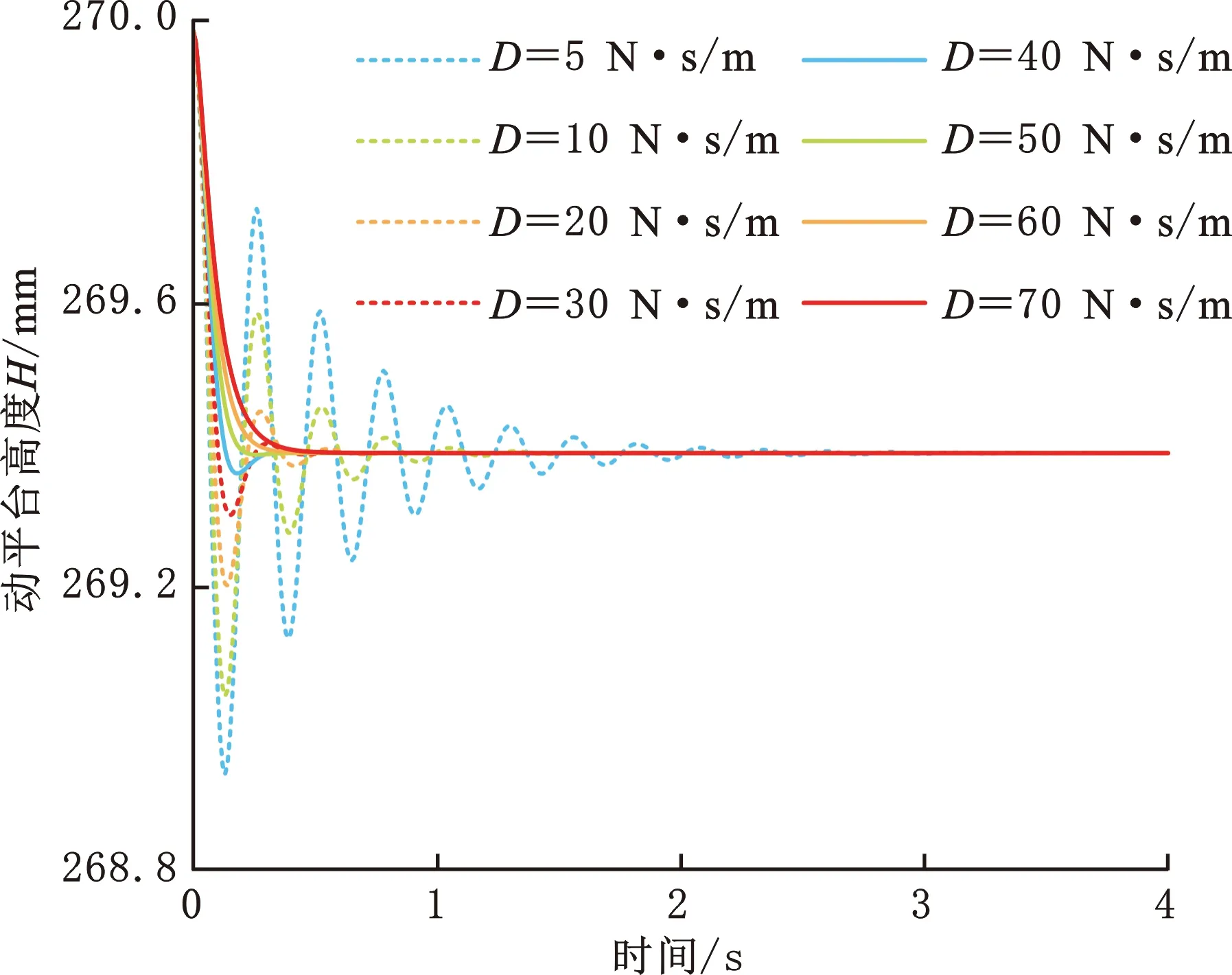
图7 D变化时动平台的高度变化(K=700 N/m)Fig.7 The height variation of moving platform when D varies(K=700 N/m)

3.2 并联平台受外力时的变化情况

向并联躯干动平台施加外力，观察并联机构驱动关节是否发生柔顺运动，判断神经肌肉控制方法是否能实现仿生并联躯干的柔顺控制。本文中所施加的外载荷分别为沿坐标轴的力和绕坐标轴的扭矩；同时，肌肉刚度K为700 N/m，肌肉阻尼D为50 N·s/m。

3.2.1施加沿Z轴的外力

动平台受力情况如图8所示。在动平台圆心，施加沿{P}坐标系Z轴负方向的力F，如图8a所示，然后观察动平台位置和姿态的变化。力的施加情况如下：0～5 s时F=0；5～13 s时F=25 N；13～21 s时F=45 N；21～25 s时F=0。

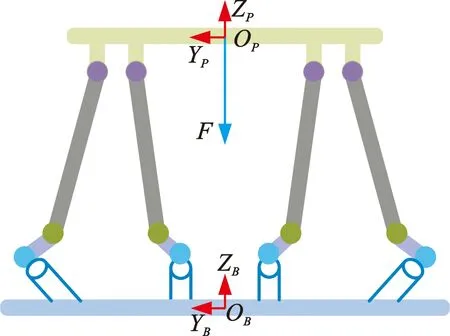
(a)施加沿Z轴的外力

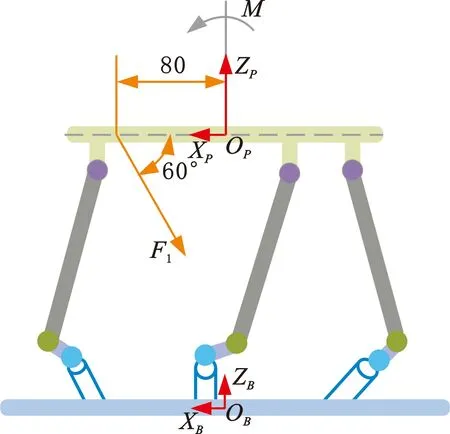
(b)施加绕Y轴的扭矩图8 动平台受力情况Fig.8 Dynamics of moving platform

若并联机构仅按照逆运动学求解的期望关节转角运动，则外力作用时，6个电机的转角始终保持在0°附近，如图9所示。采用神经肌肉控制时，并联机构在0～5 s间不受外力作用，6个电机在机构自重作用下偏转2°。5 s时施加25 N的力，电机转角增加至12°，用时0.2 s达到稳态；13 s时外力增大至45 N，电机转角为20°，响应时长为0.2 s；21 s外力撤销后，电机转角均恢复到2°并保持不变。仿真结果表明受神经肌肉控制的并联机构在Z方向的外力作用下产生了柔顺运动。

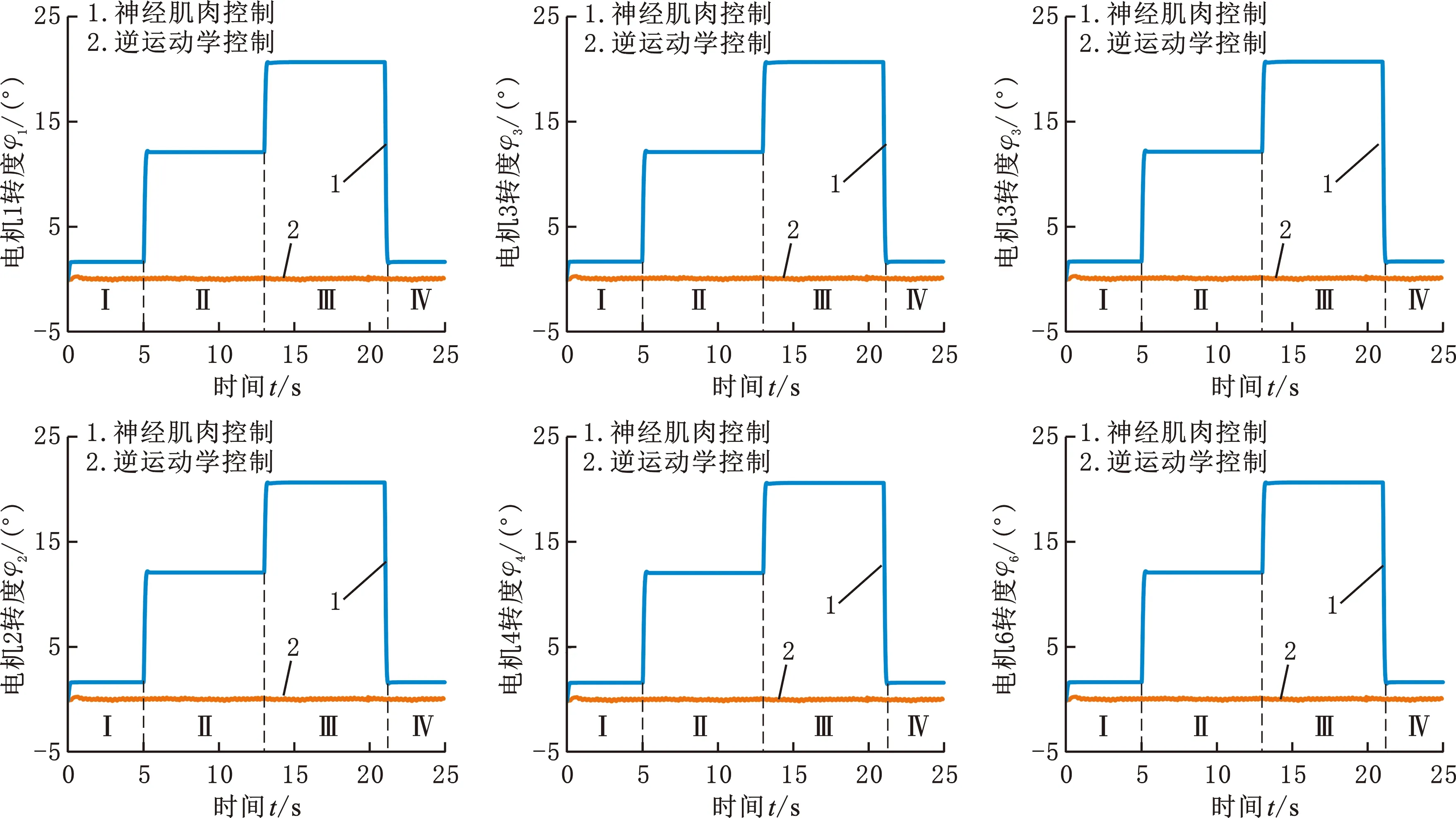
图9 在Z向外力作用下，并联平台的电机转角变化Fig.9 The variation of motor rotation angle of parallel platform under Z direction external force

3.2.2施加绕Y轴的扭矩

图8b中，与水平面夹角60°的力F1对动平台的作用效果可等效为绕Y轴的扭矩M。扭矩的施加情况：0～4 s时M=0；第4 s时M=2 N·m，并保持10.4 s；第14.4 s时M=0。

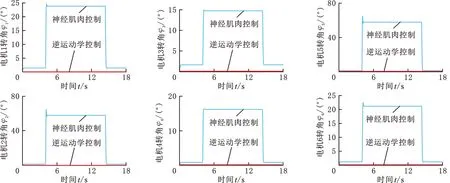
如图10所示。当并联机构仅由逆运动学控制时，对动平台施加扭矩作用，6个电机的转角均为0°。采用神经肌肉控制方法控制并联机构时，0～4 s的并联机构不受外力作用，电机转角均为2°。电机转角变化的原因是动平台和支链的总重力使肌肉模型受力，产生电机偏置角。在第4 s施加2 N·m扭矩时，动平台的俯仰角β由0°增大到5°，对应的电机2、5转过约58°，电机3、4转过约15°，电机1、6转过约21°，电机转角曲线上升所需时间约为0.2 s；第14.4 s撤销扭矩时，动平台的姿态角和6个电机转角返回初始转角0°。仿真结果表明，由神经肌肉控制的并联躯干在外界负载和干扰作用下具有一定的顺应性。

4 实验验证分析

为验证算法效果，在实验环境下，施加沿Z轴的力和绕Y轴的扭矩，观察动平台位姿和电机转角的变化，以及转角曲线上升所需时间。本实验利用NI控制板，通过LabView软件进行编程，数据通过以太网发送给NI控制板，再传送给驱动器；驱动器发送PWM波驱动直流伺服电机带动支链和动平台运动。支链上的力传感器通过采集模块与控制板卡相连。姿态传感器安装在动平台上面，通过USB通信，姿态信息传输频率为500 Hz。

4.1 施加沿Z轴的力

实验过程中施加的力与仿真施加的力一致，所得实验结果如图11所示。设定动平台的初始姿态为水平即ψ=θ=φ=0°。第I阶段(0～5 s)，仅重力作用，电机角度均在0°附近，摇杆也都保持水平。第Ⅱ阶段(5～13 s)，竖直向下的力F2=25 N，在神经肌肉控制下，6个电机转角在大约0.5 s内从0°增加至12°并保持稳定，摇杆也随电机转过相同的角度。第Ⅲ阶段(13～21 s)，竖直向下的力F3=45 N，在神经肌肉控制下，6个电机的转角在0.54 s内从12°增加至25°并保持稳定，同时摇杆也转到对应角度。第Ⅳ阶段(21～25 s)撤销所有的力；在神经肌肉控制下，6个电机的转角从25°减少至0°，动平台回到初始位姿状态，电机角度曲线下降所需时间约为0.9 s。逆运动学控制下的并联机构在整个实验过程中的电机转角和摇杆位置始终不发生变化。

(a)电机转角

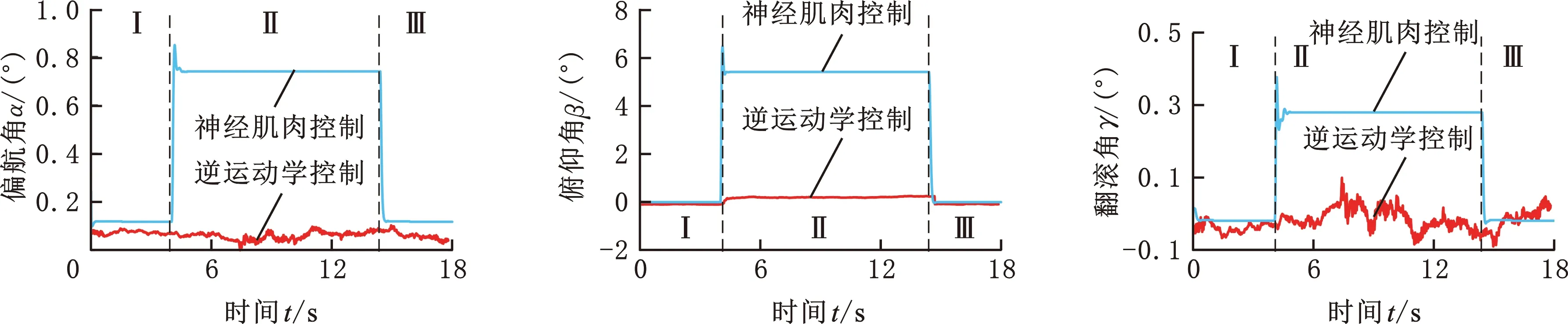
(b)动平台的姿态角图10 在绕Y轴旋转的扭矩下，并联平台的电机转角和姿态变化Fig.10 The variation of motor rotation angle and attitude information of the parallel platform under the torque of rotation around Y-axis

(a)神经-肌肉控制的实验过程 (b)逆运动学控制的实验过程

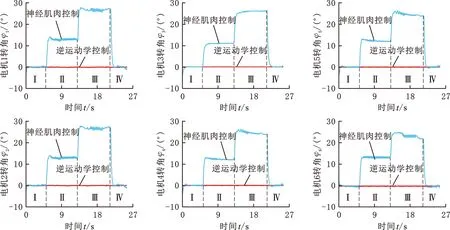
(c)电机角度变化情况图11 在沿Z轴外力下，并联躯干的柔顺控制对比实验Fig.11 Comparison experiment of compliance control of parallel trunk under external force along Z-axis

4.2 施加绕Y轴的扭矩

实验过程中施加的扭矩M=2 N·m，所得实验结果如图12、图13所示。设定动平台的初始姿态为水平即ψ=θ=φ=0°。第I阶段(0～4 s)，仅重力作用，每个电机的转角均在0°附近，每个摇杆均保持水平。第Ⅱ阶段(4～14.4 s)，施加的扭矩为2 N·m，神经肌肉控制下，动平台的俯仰角θ在0.52 s内从0°增加至6.5°并保持稳态。电机1、4的转角稳定在6°，电机2、3的转角稳定在40°，电机5、6的转角稳定在13°。第Ⅲ阶段(14.4 s之后)撤销扭矩；神经肌肉控制下，动平台俯仰角θ在0.52 s内从6.5°减少至0°并保持稳定。逆运动学控制下的并联机构在整个实验过程中的姿态角和电机角度都不发生变化。

(a)神经-肌肉控制的实验过程 (b)逆运动学控制的实验过程图12 在绕Y轴旋转的扭矩下，并联躯干的顺应性姿态控制对比实验过程Fig.12 Contrastive experimental process of compliance attitude control of parallel torso with torque around Y axis

(a)动平台的姿态角

(b)电机角度变化情况图13 在绕Y轴旋转的扭矩下，并联躯干的顺应性姿态控制对比实验结果曲线Fig.13 Contrastive experimental result curve of compliance attitude control of parallel torso with torque around Y-axis

5 结论

本文分析了仿生并联躯干的正逆运动学，建立了仿生肌肉控制模型，提出了基于神经肌肉控制架构的仿生并联躯干控制方法，在保证仿生并联躯干快速响应的前提下，增强了其对外部冲击的柔顺性。通过仿真分析了肌肉控制模块的柔顺特性和响应特性，通过实验验证了所提控制策略的有效性和可实现性。依据仿生理念，神经运动控制网络还可用于生成仿生躯干的不同运动模式。肌肉参数的调节与优化还能进一步提高仿生躯干的柔顺运动性能。神经肌肉控制方法还可以与轨迹规划方法、动力学控制等方法结合来进一步提高仿生躯干运动的柔顺性和稳定性。后续我们将对肌肉刚度的自适应调节和仿生躯干的姿态闭环控制进行研究，搭建具有仿生并联躯干的四足机器人，重点研究并联躯干对机器人整体及运动性能的影响。