一种新型附加稳定链锚泊系统的静动力特性分析

张宸鑫，李效民

（中国海洋大学工程学院，山东青岛 266100）

0 引 言

海洋油气浮式生产结构的定位主要分为悬链式锚泊系统和张紧式锚泊系统两种形式。悬链式锚泊系统随水深增加而产生的水平刚度降低、覆盖海域面积大等问题限制了结构的发展，降低了承载能力[1]。张紧式锚泊系统与海床缺乏接触段，形成的拉力提升角对抛锚点产生较大垂向锚固力，对锚的垂向抗拔性能带来隐患[2]。所以亟需探索一种融合两种锚泊系统优势的新型锚泊系统。

附加重块的锚泊系统（图1所示）能够结合上述两种锚泊系统的优势，使锚泊系统在预张力较小的情况下获得较大的回复力，不仅强化了锚泊系统的疲劳强度和定位稳定性，也降低了成本[3]。Yuan等[4]对靠近海床处固定重块的新型锚泊系统进行性能评估，证实了附加重块可以改善垂向抗拔性能和降低顶部张力。但在极端环境下重物会脱离海床，悬挂延伸成链的一部分，使锚泊系统形态急剧不稳定[5]。Gurung 等[6]在缓波型挠性立管的弯拱处布置稳定链，结果表明，稳定链对柔性立管的性能具有改进作用，降低了碰撞风险，改善了线铺设方位角。但在当前锚泊系统研究中，尚未发现采用稳定链替代重块的模型，因此，本文提出一种附加稳定链的新型锚泊系统，验证其在降低竖向轴力的同时，控制缆索与海床垂向距离，避免产生过大的集中作用力，从而减小辅助设备对缆索性能产生不良影响的作用。

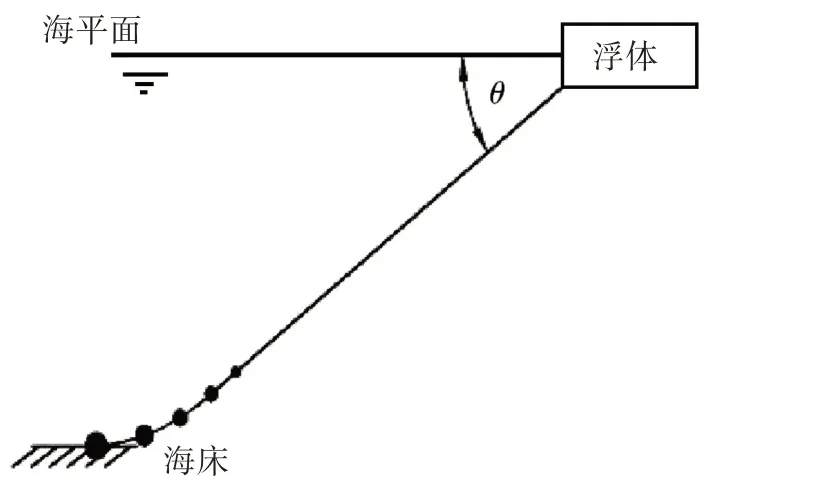
图1 附加重块的锚泊系统示意图Fig.1 Mooring system with weighted blocks

在研究锚泊系统非线性特性时通常采用悬链线方程、分段外推法、有限元法和集中质量法等传统建模方式，这些数学方法通常以连续介质力学思想为基础，在数据处理过程中具有一定的复杂性。从Ji等[7]采用悬链线方程法对新型锚泊系统的分析中了解到，悬链线方程在使用过程中遵循忽略链索弹性变形及流体力作用的假设，使得数值模拟结果与真实情况之间产生一定的误差。乔东生等[8]采用分段外推法对串联浮筒锚泊系统进行了优化设计。分段外推法在处理附加辅助装置时，每增加一个浮筒就需增加一段迭代求解过程，处理过程表现出一定的复杂性。Jaw 等[9]通过有限元方法对单点多段锚泊系统建立数学模型，采用增量法和迭代法对离散方程进行时间积分，此过程增加了数据运行的难度。Xiong 等[10]采用集中质量法分析了吸力锚的锚点、触点截断和导缆孔的复杂动力响应。虽然计算结果较为精确，但触点截断计算时的边界条件变化以及对应控制方程的模拟都给分析研究带来困难，使得求解过程变得复杂。

本文选取的向量式有限元法是一种结合向量力学和数值计算的物理模型，核心思想是将缆索离散为相互独立的系列质点集合，质点间由只存在内力而没有质量的杆件元连接，通过对质点的运动变形以及位置变化来模拟锚线在真实情况下的运动[11]。其优势在于将结构体静动力特性分析有机统一在一种建模方式中，不需要集成刚度矩阵和迭代求解控制方程，就能预测结构体的运动过程和动力响应[12]。李效民等[13]采用向量式有限元对顶张力、悬链线立管及惰型立管等典型柔性海洋管道进行动态行为分析，证明了向量式有限元法通过采用物理模式和显式中央差分法所带来的简化分析难度的优势，在海洋工程领域中处理复杂边界条件下的几何非线性问题方面具有极好的应用前景。

本文首先系统地介绍了向量式有限元的理论概念，运用Matlab对新型锚泊系统进行数学建模，分析了不同工作条件下模型的有效张力和位型，并将结果与传统有限元法进行比对，验证向量式有限元法的准确性。之后，在Yuan 等[4]提出的新型锚泊系统基础上，用具有自我调节机制的稳定链替换重块，考虑上端浮体运动影响以及复杂环境作用，通过模型敏感性研究来探索重块和稳定链间的工作性能差异。

1 锚泊系统的建模及求解

1.1 向量式有限元的基本概念

向量式有限元法以点值描述、途径单元和虚拟逆向运动[15-16]为基本框架，可对多个连续结构体间运动、变形等相互作用进行模拟。

如图2 中杆件（a-b）被离散为有限数量的质点，转换点值描述对象为空间点位置和点上的载荷作用，整个缆索的运动和变形通过质点运动和位置变化来描述。在物理意义上，点值描述舍弃了复杂的分析力学方式，直接用牛顿定律表示点的运动，用有限数量点单元位移和点力描述载荷和约束条件[16]。建立理想化模型时，锚泊系统的任一质点I的等效质量mi可表达为下式：

图2 点值描述Fig.2 Point value description

式中，mi是包括集中质量和杆件元质量的等效质量，M为空间点上的集中质量，杆件等效质量Mi=ρV/2是将实际杆件上的总质量平均分配在杆两端的连接质点上。

为了简化内力并对不连续结构进行处理，可以利用时间途径将锚泊系统模拟运动时间历程划分为一系列独立的连续途径单元。在本构关系中，结构在空间上限制在一个结构单元内，在时间上限制在途径单元内。图3 为点I从t0到tf的运动轨迹，取一组微段，用ta、tb分别表示初始时间和终结时间，模拟点I在该途径单元上的空间位置向量及运动过程。质点运动方程为

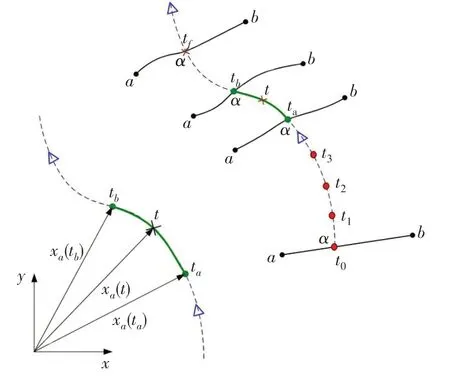
图3 途径单元Fig.3 Path unit

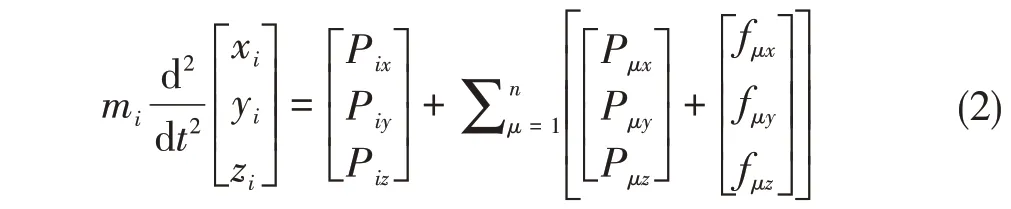
式中，Pμ和fμ是杆件元提供的等效作用力及节点内力，n为杆件元总数。

采用合适的单元可以使变形近似看成均匀变化，力的计算也可以转化成小变形、小变位的问题。图4 以ta初始时刻型态为基础构架，途径单元内任意时刻t的位置向量发生平移（-u1）和转动（-θ）的逆向运动，分别得到杆件位置（1'-2'）和杆件位置Vd(1d-2d)，这个过程与材料力学中轴力元件的基本假设相符，最后通过虚拟逆向运动得到消除平移和转动的锚泊系统的纯变形。

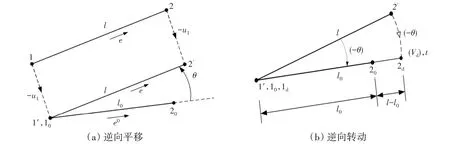
图4 逆向运动Fig.4 Inverse motion

综上所述，向量式有限元法基于牛顿力学，模拟过程中遵循运动定律和胡克定律。在分析单元结构的时候，类似将杆件的变形过程分解为一系列时间点集合，单独对这些时间片段求解。每一个结构单元相对独立，内力变化也只计算两个时间点之间的内力变化。这种计算在时间途径单元内连续，但在整体时间段上不连续，因此在时间点上，复杂边界条件变化时，只需在该质点位置处根据真实情况增减不同方向的集中载荷来替代模块作用，这对于处理重块、稳定链等辅助设备所带来的复杂边界变化具有极大优势。

1.2 锚泊系统内力计算

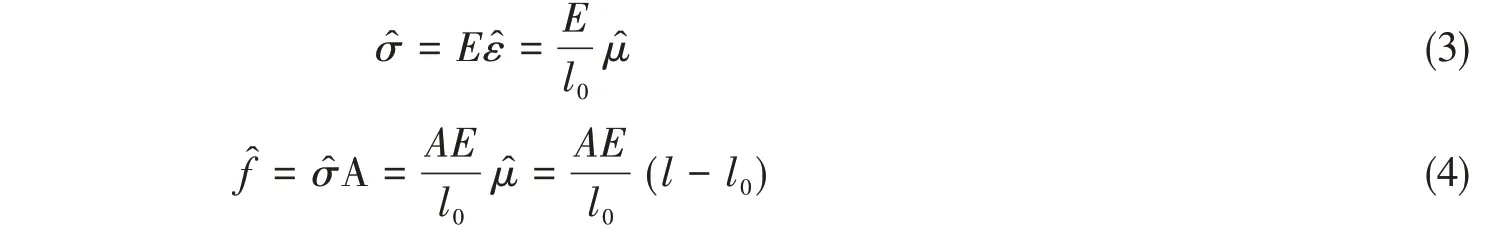
式中，E为弹性模量̂为微应变，l0为杆件元变形前长度̂为变形函数，A为截面积，l为杆件元变形后长度。改写系泊缆索轴力公式（4）成节点内力表达式为

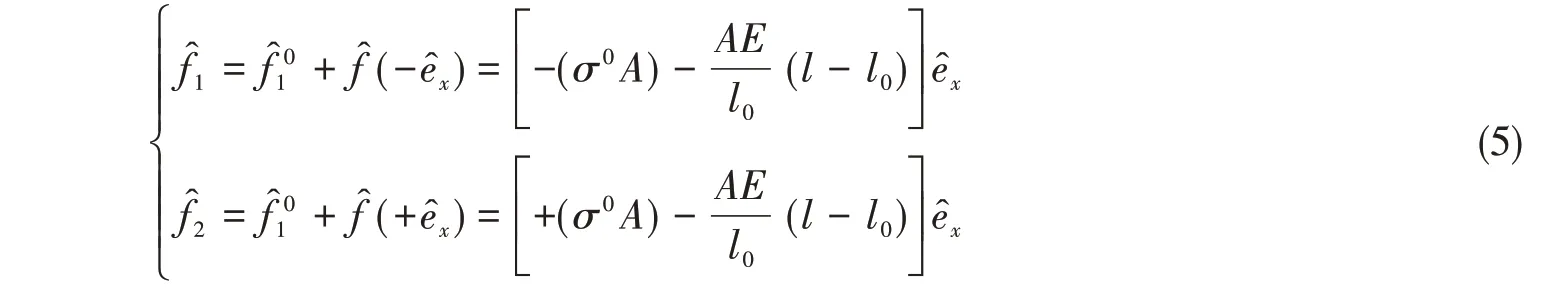
再通过正向运动使经过虚拟逆向运动的结构体回到原位置，这个过程中力的量值不发生改变，只有方向做向量转动，所以

式中，f1、f2是指空间点所提供的杆件元节点内力。

1.3 控制方程的求解

为了避免隐式差分可能带来的迭代和收敛等复杂问题，本文采用显式时间积分法，通过点运动循环和内力循环进行计算。转换公式（8）的差分计算可表达为

1.4 锚泊系统模型的建立

锚泊系统的整体坐标系如图5 所示。以O点作为缆索与海床接触的锚固点，向上均匀划分单元节点为1，2，···，i，j，···，N，N+1。对于缆索的初始位型，假设初始是具有一定倾角的无重斜直杆，底端铰接。可采用载荷控制或位移控制解决初值和边值问题，在指定时间内，将第N+1质点从A移动至目标位置B，同时以斜坡加载函数方式将载荷施加到缆索上，形成最终初始目标位型。

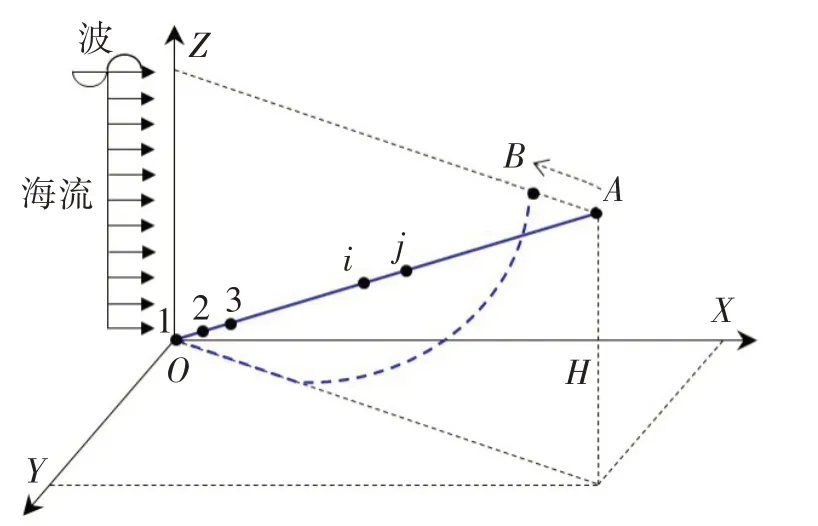
图5 锚泊系统坐标示意Fig.5 Coordinates of mooring system

1.5 海床土模型

悬链线形状使拖地段与海床相互作用，考虑海床土与锚泊系统间的接触摩擦，可以避免失稳或者疲劳断裂状况可能带来的损失。本文采用线性截断弹簧模型及库伦摩擦力模型来模拟海床土体实际情况（如图6所示）。海床土摩擦力表示为阶梯方程式：

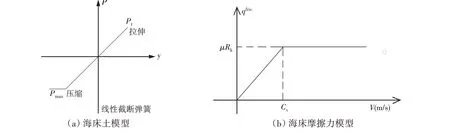
图6 海床土体的模拟Fig.6 Simulation of seabed soil

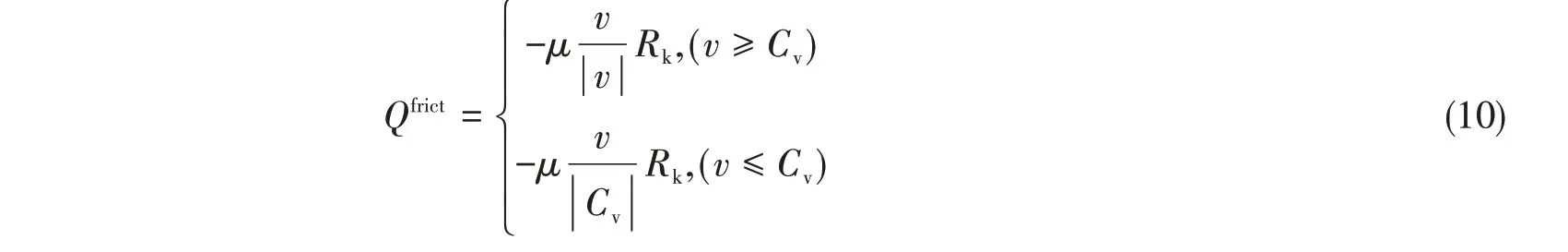
式中，μ为摩擦系数，Rk为竖向支持反力，Cv为切向速度限制，v为拖地段移动速度。

2 附加稳定链张紧式锚泊系统静动力特性分析

2.1 静水平衡状态验证

采用向量式有限元法验证水深1000 m的FPSO系泊效果，并与图7中的三种锚泊系统进行对比[4]。复合锚泊系统链长1896 m，划分为105段，材料特性如表1所示。

图7 三种不同锚泊系统Fig.7 Three different mooring systems

表1 系泊缆索材料特性Tab.1 Material properties of mooring cables

锚泊系统在静水平衡状态下的位型与张力如图8 所示，从图8（a）截取海床以上60 m 部分位型细节图可看出，TML 呈近似张紧的直线形状，HMSW 和HMSWB 呈现出悬链线特性，存在拖地段。图8（b）为稳定状态下的静张力，三种模型的张力总体呈增大趋势，中部张力增长缓慢，这是因为聚酯绳质量轻于上下段钢链。HMSW 模式由于底部重块的存在，使得张力值偏大于TML 模式。对比采用向量式有限元法得到的结果与传统有限元方法的结果，发现向量式有限元对复合锚泊系统的模拟准确且有效，在位型预测及张力分析等方面的吻合程度较高、可实施性程度较好。

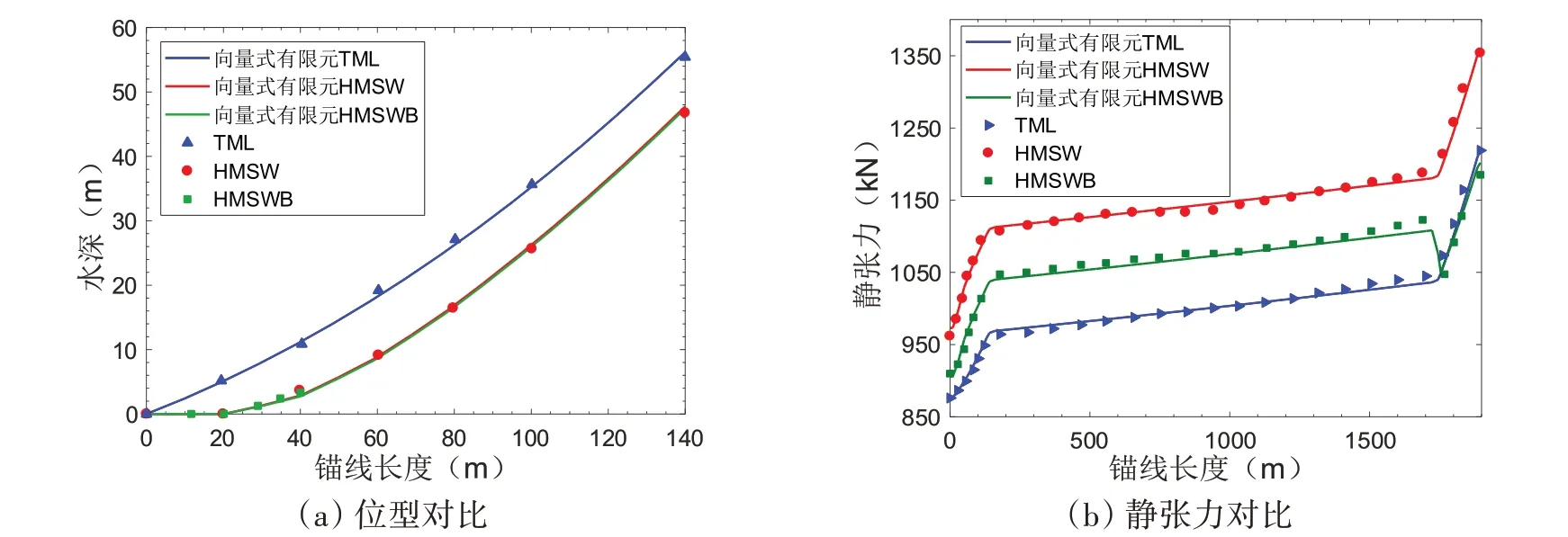
图8 新型锚泊系统位型和张力对比图Fig.8 Comparison of configuration and tension of new mooring system

2.2 环境载荷作用分析

在上述材料及布置方案基础上，采用稳定链替代重块的设计形式，连接方式与重块的连接形式相同。在抛锚点向上串联布置5 条统一特性稳定链，相互间距为20 m（如图9 所示）。分别对三种不同辅助装置锚泊系统的性能进行数值模拟：布置重块、单一稳定链及复合稳定链模式。单一稳定链材质按表2 上部材料设置；复合稳定链材质完全按照表2 所展示的材料特性。详细的环境载荷见表3。

表2 稳定链材料特性Tab.2 Material properties of stable chain

表3 环境载荷参数Tab.3 Environmental load parameters

图9 附加稳定链锚泊系统Fig.9 Additional stable chain mooring system

附加稳定链或重块会促使锚泊系统结构在锚固点附近发生悬链形变，往往带来海床摩擦效应。图10是海床摩擦作用影响锚泊系统位型和张力时程的对比图。从图10（a）截取的海床以上60 m 部分位型细节图可以看出，HMSW 和附加稳定链模型由于重块重力影响使下端线形发生变化，HMSW 呈现为存在拖地段的悬链线状，减缓了拉力提升角。无附加任何重块或者稳定链的锚泊系统呈张紧状，其余两种模型的位型处于上述两种情况之间，轻微海床摩擦作用对链型影响不大。图10（b）中，稳定链使锚泊系统位型发生微妙变化，同时可以控制张力在一定范围内，这是由于重块重力的影响使拖地段长度增大，与海床土接触产生的相互作用力变大。总之，海床土作用力的强弱与锚泊系统的链型有关，而稳定链的存在可以在一定程度上控制链型变化。

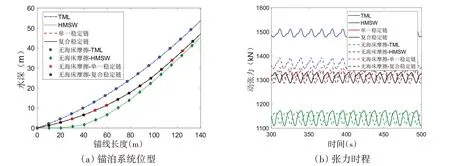
图10 海床作用下的锚泊系统位型和张力时程Fig.10 Configuration and time history of tension under seabed action

图11是TML、HMSW、单一稳定链、复合稳定链的上部浮体纵荡、垂荡运动下的时程张力图。在纵荡运动和垂荡运动中，由于重块重量会增大顶部张力，浮体的牵伸也会随之增大，所以HMSW 的动张力最大，而稳定链可以有效地控制重块的重力大小从而约束了顶部张力。图中都可以看出单一稳定链与复合稳定链仅存在可忽略不计的细微差距，因此设计时可优先考虑安装简单、成本低廉的串联单一稳定链的锚泊系统。

图11 纵荡、垂荡运动引起的张力时程Fig.11 Time history of tension induced by surge and heave motion

2.3 动张力曲线及频谱分析

锚泊系统频繁出现张紧—松弛状况会大幅度减弱稳定性，加快出现疲劳损伤危险。为了预测出现张紧—松弛状态的条件，探索稳定链和重块在相同工况作业下的性能特点，分别对动张力曲线及频谱、上部浮筒振荡进行分析。设置预张力Fp为2233 kN，顶端单元正弦位移激励作用产生动张力，振幅Am以0.5 m 为间隔从0.5 m 到5.0 m 增加，频率f以0.1 Hz为间隔从0.1 Hz增加到2.0 Hz[17]。本文选取位移激励振幅Am=1 m 时，20 组不同频率激励的详细变化趋势进行展示，其他振幅下激励结果与本组实验结果变化趋势相似。

首先依次选取f为0.1 Hz、0.3 Hz、0.6 Hz、0.8 Hz和1.0 Hz 5种频率进行分析与讨论，取出平稳段下的数值进行处理，得到的曲线和频谱见图12～16。

由图12 到图14 可以看出，低频激励作用下的锚泊系统处于张紧状态，且各点处张力均不超过预张力值，动张力曲线的形态表示为不同频率正弦曲线的叠加；从频谱图可以看出，动张力频率产生倍频成分，但其值很小。由图15～16 了解到，随频率的增大，最小张力值已经小于0，说明锚泊系统状态发生转变，由张紧转变为松弛—张紧，此时动张力的峰值也超过预张力值（图中水平黑线为预张力Fp=2233 kN基准线），动张力值变化曲线开始杂乱无章，频谱图也出现多成分高频成分。说明动张力呈非线性上升变化，而一旦链型由张紧状态进入松紧—张紧状态，那么动张力值将会显著上升。

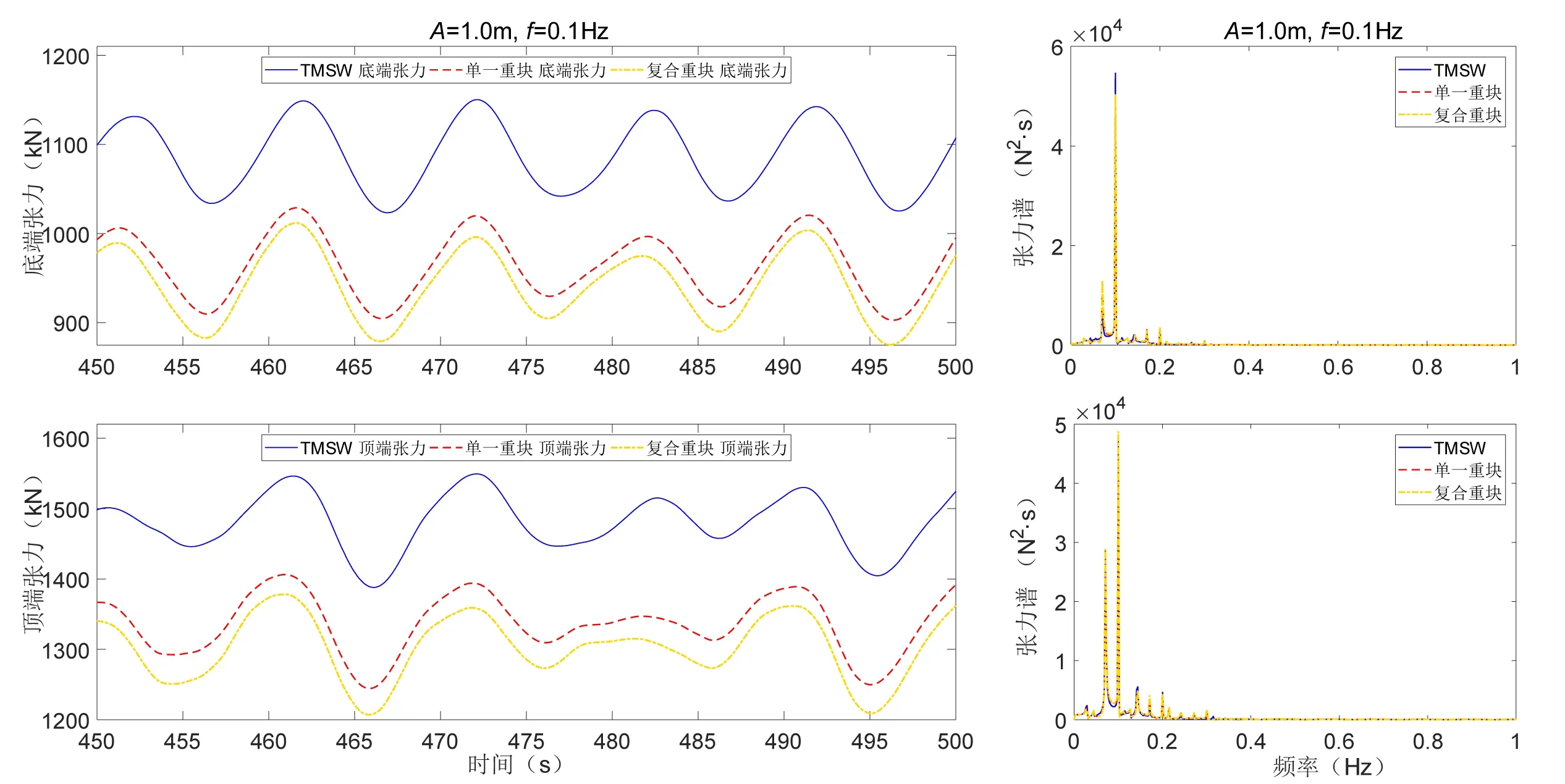
图12 f=0.1 Hz下动张力曲线及对应频谱图Fig.12 Dynamic tension curve and spectrum diagram at f=0.1 Hz

图13 f=0.3 Hz下动张力曲线及对应频谱图Fig.13 Dynamic tension curve and spectrum diagram at f=0.3 Hz

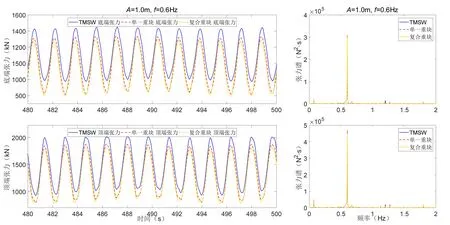
图14 f=0.6 Hz下动张力曲线及对应频谱图Fig.14 Dynamic tension curve and spectrum diagram at f=0.6 Hz

图15 f=0.8 Hz下动张力曲线及对应频谱图Fig.15 Dynamic tension curve and spectrum diagram at f=0.8 Hz

图16 f=1.0 Hz下动张力曲线及对应频谱图Fig.16 Dynamic tension curve and spectrum diagram at f=1.0 Hz

单独分析三种不同模式，从图12～16 可以看出，在相同激励下，串联重块的TMSW 锚泊系统所受的动张力值最大，其次是单一稳定链。原因是稳定链的存在使得锚泊系统下端所受重量可根据与海床之间距离进行变化，而复合成分稳定链更是发挥了可变质量这一优势，让稳定链的质量形成阶梯增加状态。但从图15～16可以看到，当锚泊系统进入松弛—张紧状态后，三种形式下的锚泊系统动张力时程曲线图交织在一起。

下面对f为1.2、1.4、1.6、1.8和2.0 Hz 5种更高频率下的锚泊系统动张力进行展示与分析，如图17～21所示。

从图17 到图21 看出，激励频率的增大并没有使松弛—张紧状态再发生转变，最大动张力均大于预张力值。频谱图中动张力的频率成分包含了高频成分、低频成分和激励频率，在锚泊系统底端处的频谱图较顶端处的激烈，高频成分出现次数较高。

图17 f=1.2 Hz下动张力曲线及对应频谱图Fig.17 Dynamic tension curve and spectrum diagram at f=1.2 Hz

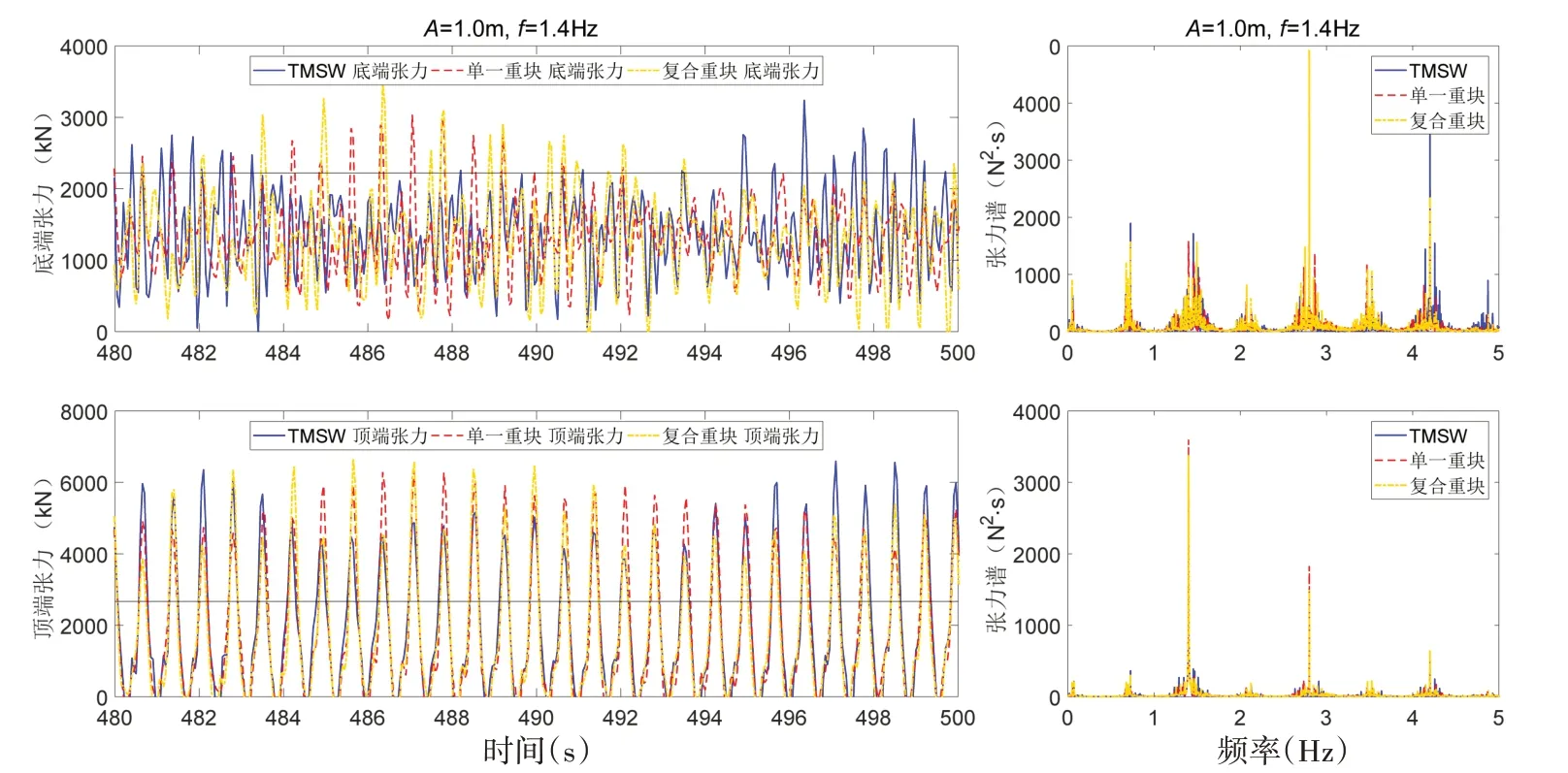
图18 f=1.4 Hz下动张力曲线及对应频谱图Fig.18 Dynamic tension curve and spectrum diagram at f=1.4 Hz

图19 f=1.6 Hz下动张力曲线及对应频谱图Fig.19 Dynamic tension curve and spectrum diagram at f=1.6 Hz

图20 f=1.8 Hz下动张力曲线及对应频谱图Fig.20 Dynamic tension curve and spectrum diagram at f=1.8 Hz

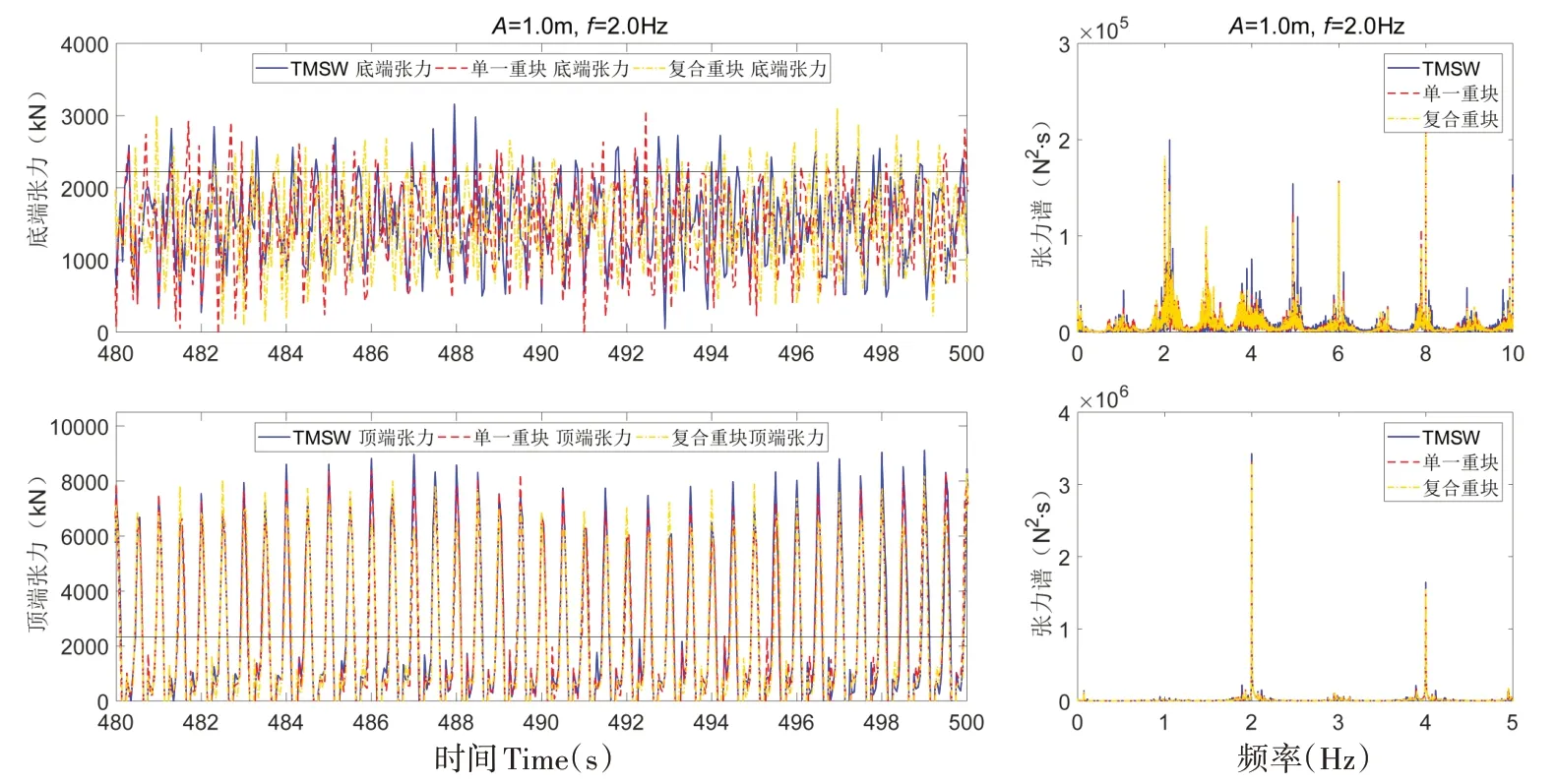
图21 f=2.0 Hz下动张力曲线及对应频谱图Fig.21 Dynamic tension curve and spectrum diagram at f=2.0 Hz

2.4 最大及最小动张力值

当锚泊系统进入松弛—张紧状态后，该时刻的动张力变化显著，锚泊系统内产生了冲击张力。为了探索冲击张力产生的条件，保持预张力2233 kN不变，将上部激励的10种振幅和20种激励频率所组成的工况进行模拟，比较稳态时刻的动张力曲线图，展示不同激励下的动张力最大、最小值图。

由图22可以看到，在多组不同激励幅值条件下，锚泊系统的最大动张力值随频率的增大呈波动上升趋势。单考虑振幅影响时，振幅越大，最大动张力值越大，在不同振幅作用下，锚泊系统进入松弛—张紧状态的频率不同，激励的振幅越大，进入松紧—张弛状态所需频率越小，且在相同频率下，幅值越大动张力的峰值越大。从最小值可以看出，在频率大于1.6 Hz时，所有工况下的最小动张力达到0，是系泊缆进入松弛—张紧状态，但当激励频率较小时，受高振幅影响的锚泊系统尚未进入松弛状态。

图22 不同激励下的动张力最大、最小值随频率变化曲线Fig.22 Maximum and minimum dynamic tensions under different excitions

3 结 论

本文基于向量式有限元法建立了张紧式锚泊系统的运动分析模型，编制的Matlab 程序分别实现了锚泊系统在静水平衡状态及串联稳定链状态下的响应分析。结果表明，向量式有限元法的最终结果与传统数学建模方法十分吻合，可作为一种新型数值模拟方法应用到锚泊系统的特性分析中，尤其适合串联重块或稳定链这种具有复杂边界条件的结构系统，可为此类锚泊系统的应用提供理论和数据支持。通过分析，得到以下结论：

（1）向量式有限元法与传统有限元法在位型预测和张力分析方面的吻合度较高。

（2）附加不同材质辅助设备会对张紧式锚泊系统的张力值及垂向抗拔性能产生不同影响。沿海底延伸的稳定链可以减缓拉力提升角度和所需垂向锚固力，相较于附加恒定质量重块模型，稳定链模式具有在运动响应不受影响的前提下，降低顶部张力并限制海床接触风险、提高运行寿命和成本效益的优势。

（3）张紧式锚泊系统状态转变会对工作性能带来不利影响。在顶端激励作用下，锚泊系统的最大动张力值会随频率的增大呈波动上升趋势，且振幅越大，最大动张力值越大，当锚泊系统进入松弛—张紧状态时，出现显著最大动张力。激励的振幅越大，进入松紧—张弛状态所需的频率越小。研究锚泊系统状态转变条件对防止整体结构断裂破坏和疲劳损伤有极大的帮助。