一种复合式非线性低频隔振器的隔振特性分析

李小彭，孙万琪，尚东阳，轩诗雨

（1.吉林大学汽车仿真与控制国家重点实验室，长春 130025；2.东北大学机械工程与自动化学院，沈阳 110819）

0 引 言

舰船上的动力设备在工作时产生的低频振动由于其高传递性和低衰减性，一直是威胁舰船隐蔽性的主要因素[1]，同时舰船设备由于其工作环境的特殊性，要求隔振系统具有一定的高静低动的刚度特性，因而构建合适的减振系统以提高舰船的隐蔽性及存活率是目前水下减振研究的主要方面。隔振系统根据是否需要外部能量输入可以分为主动隔振与被动隔振，主动隔振系统虽然效果有所提升，但其设备的复杂性以及维护的不便性限制了其在舰船工程方面的应用。被动隔振由于其结构简单、可靠性高、无外加能量，仍然有着广泛的工程应用空间[2]。

传统被动隔振能够隔离大部分高频振动，但却对低频振动的隔离效果较差[3]。何琳等[4]系统地介绍了我国船舶隔振的发展历程，其隔振的核心问题是在如何能够保证系统稳定性的前提下尽可能地降低低频振动；为了解决这一问题，邓辰鑫等[5]基于惯容器构造了主动惯容控制策略，提高了列车的低频隔振能力；吴庭等[6]将惯容器与蓄能器相结合构造出复合式低频隔振器；包国志等[7]利用磁流变阻尼器研究了船舶双层隔振系统的非线性动力学特性；朱翔等[8]针对舰船的低频线谱研究提出了一种新型惯容式动力反共振隔振器，实现良好的低频线谱隔振；刘彦[9]将惯容器分别以不同的方式与传统隔振与吸振系统相结合，研究表明加入惯容器后在不改变原系统高频隔振的基础上，能够大幅提升系统低频的效果；郭俊华等[10]针对惯容器在船舶隔振领域的深入应用，提出一种新型的惯容-橡胶复合系统的传递率计算方法，并利用实验证明了该方法的有效性。

高静低动的刚度特性既能够增强系统的侧向稳定性，也能够扩展其隔振带宽。为实现这一特性，李爽等[11]基于机械弹簧和双环永磁体设计了一款具有高静低动特性的隔振器；程春等[12]根据高静低动隔振器的特点提出一种时滞立方位移反馈控制策略；余慕春等[13]以水和疏水沸石颗粒为介质构建分子弹簧隔振器，并以此实现高静低动的非线性刚度；杨志荣等[14]将屈曲圆板和线性弹簧组合构成非线性隔振器，并利用有限元软件分析了该隔振器的高静低动特性；柴凯等[15]针对潜艇设备低频振动的难题，提出一种具有高静低动刚度特性的三磁体型隔振器。

为了满足舰船设备的隔振需求，本文通过斜置式惯容结构获得了关于惯容器的非线性特性，并将其与经典ISD（inerter-spring-damper）隔振器相结合，构造出一种复合式非线性低频隔振器（compound nonlinear vibration isolator，CNI），能够同时满足低频隔振及高静低动刚度的要求。对该非线性隔振器进行了动力学建模，并与经典ISD隔振器和经典QZS（quasi-zero stiffness）隔振器对比，分析其隔振效果；同时分析了系统结构参数对于频响及力传递的影响，为船舰低频隔振系统的设计提供了理论指导。

1 数学模型

1.1 斜置式惯容结构模型

斜置式的惯容结构如图1 所示，该结构主要由在A点相互铰接的两个惯容器组成，惯容器的另一端点分别固定于O1和O2点，且两点相距2l。假设铰接点A始终位于O1O2连线的中线上，故惯容器的终端始终沿垂直方向移动，移动距离为x。θ表示惯容器与水平线间的夹角，分析可得

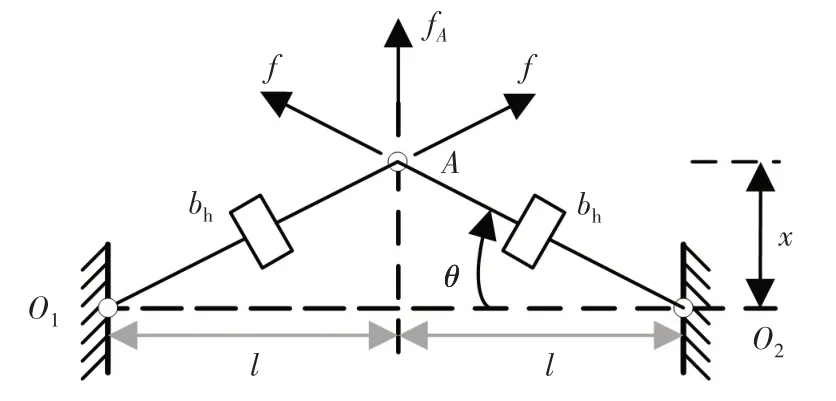
图1 斜置式惯容结构Fig.1 Inclined inerter structure

根据该斜置结构可知，沿惯容器轴向的力为

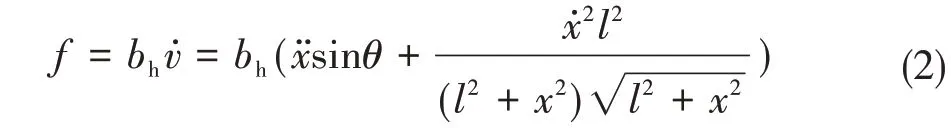
沿垂直方向的力可表示为

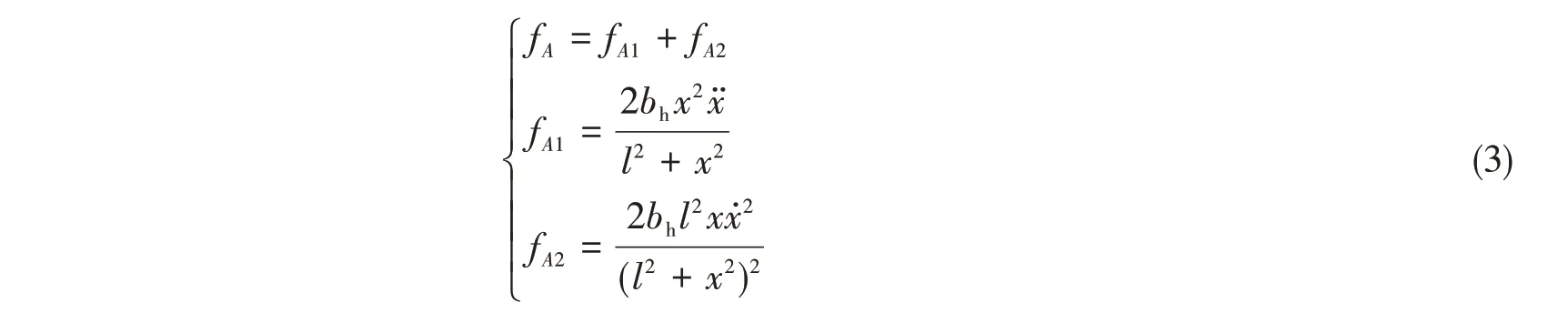
通过式（3）可以发现该结构所受到的力fA与惯容器终端A点的位移、速度以及加速度均有联系，这与经典ISD隔振结构形成了一定的对比，经典ISD隔振的作用力仅与惯容器端点的加速度有关。为了更直观地对其联系进行分析，假设惯质系数bh=0.8 kg，距离l=1.3 m，分析结果如图2所示。

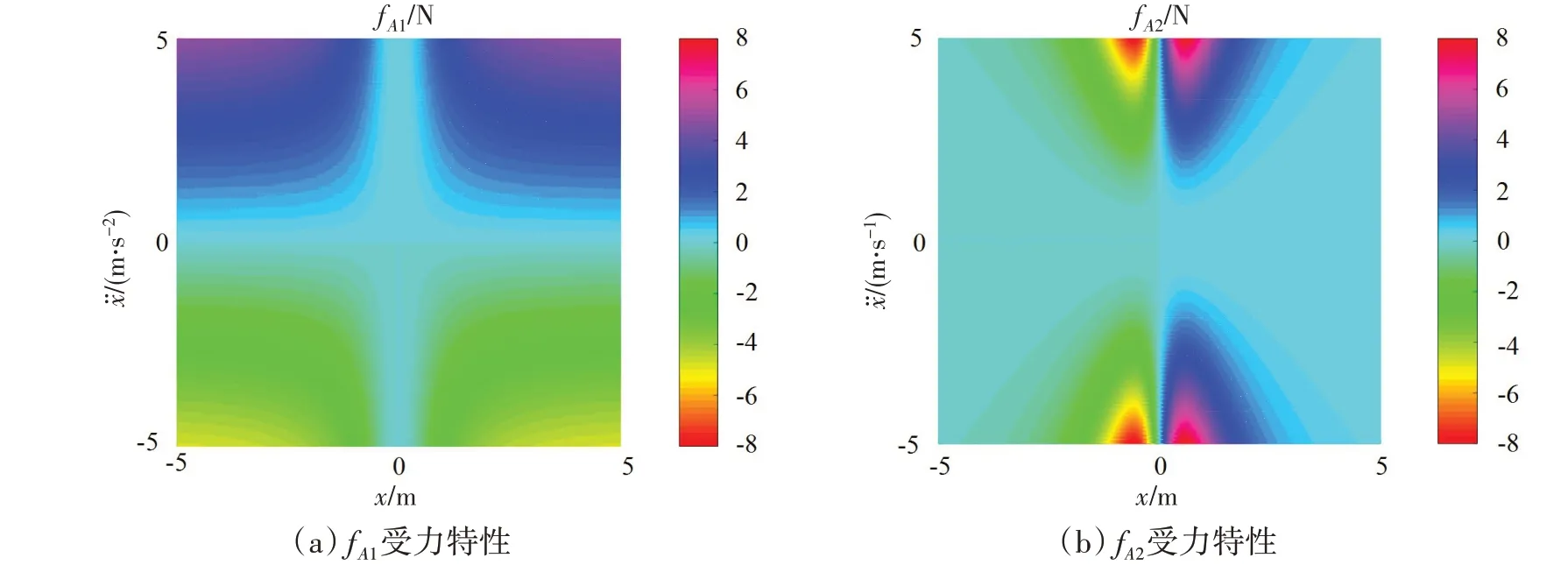
图2 斜置式惯容受力特性Fig.2 Oblique inertial capacity force characteristics

观察图2 可以发现斜置式惯容受力呈现出一定的非线性特质，fA1与终端的加速度ẍ成正比，而fA2与其终端速度ẋ的平方成正比。同时图2（b）表明fA2在位移x=0处对于速度的变化非常敏感，当位移逐渐增大时，fA2逐渐向0贴近。

1.2 隔振器动力学建模

将斜置式惯容结构引入隔振器的设计，构建一种CNI 隔振器，如图3（a）所示。同时为了对比分析，分别构建经典QZS隔振器和经典ISD隔振器，如图3（b）和图3（c）所示。

图3 不同类型的隔振器Fig.3 Different types of vibration isolators

图3（a）中的CNI 隔振器主要由一对刚度系数为kh/2 的横向弹簧、一对惯质系数为bh/2 的惯容器、刚度为k的支撑弹簧、惯质系数为b的惯容器以及阻尼系数为c的阻尼组合而成；图3（b）中的经典QZS隔振器相对于非线性CNI隔振器没有了惯容器这一元件；而图3（c）中的经典ISD隔振器仅由支撑弹簧k、惯容器b以及阻尼c组成。同时x表示质量块m在垂直方向上的位移，F表示质量块m所受到的激励力；并且在图3（a）及图3（b）中设定当位移x=0 时，横向弹簧恰好处于水平状态，并且横向弹簧及惯容器两端点距离为l，而横向弹簧原长为l0，为了获得一定的准零刚度特性，设定l＜l0。

对图3（c）中的经典ISD隔振器进行动力学分析，可得

式中，f表示激励力F的幅值，ω表示激励力的频率，x表示质量块的位移，ẋ表示质量块的速度，ẍ表示质量块的加速度。

根据图1斜置式惯容结构可知，图3（a）中CNI隔振器的纵向弹簧及横向弹簧的联合恢复力为

CNI隔振器的动力学方程为

为了简化计算，对式（6）进行无量纲化处理，令

式中，ω0表示系统的固有频率，μ表示无量纲化后的时间，λ表示系统的惯质比，λh表示斜置系统的惯质比，ξ表示系统阻尼比，L表示弹簧长度比，X表示无量纲化后的位移，K表示弹簧刚度比，Fw表示无量纲化后的激励比，ϖ表示无量纲化后的激励频率比。

将无量纲化后的结果式（7）代入式（6）可得

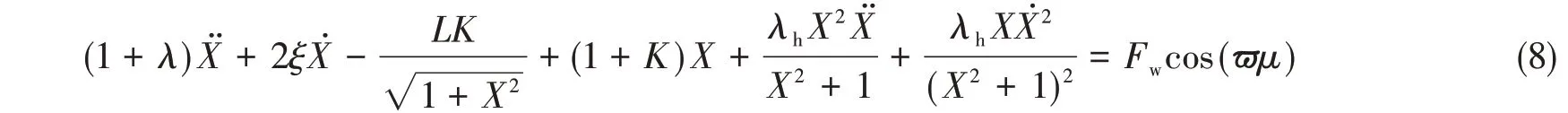
当X很小时，根据泰勒公式可得

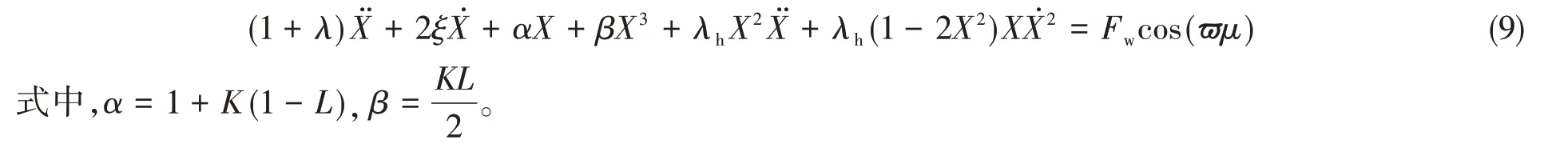
为了更加准确地描述上述隔振系统的动态响应，令质量块的位移、速度以及加速度分别为

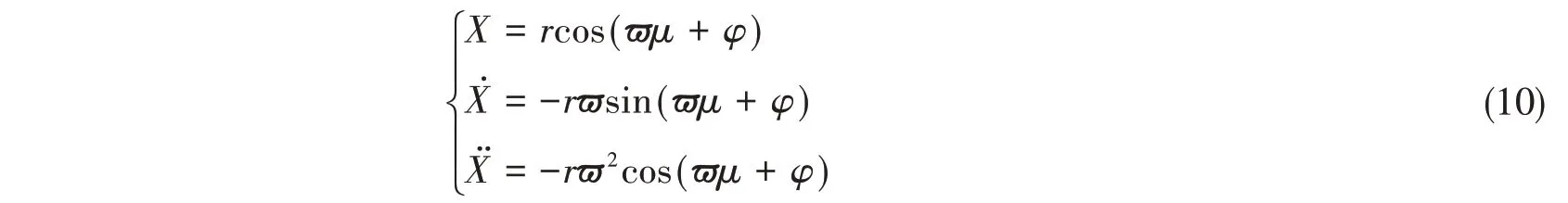
式中，r表示响应的幅度，ϖ表示响应的频率，φ表示响应的相位角。

将式（10）代入式（9）并经过变换可得

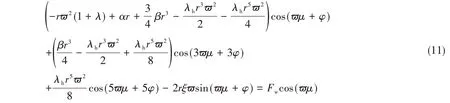
为了简化计算，本文仅考虑激励频率附近的系统动力学响应，故可得

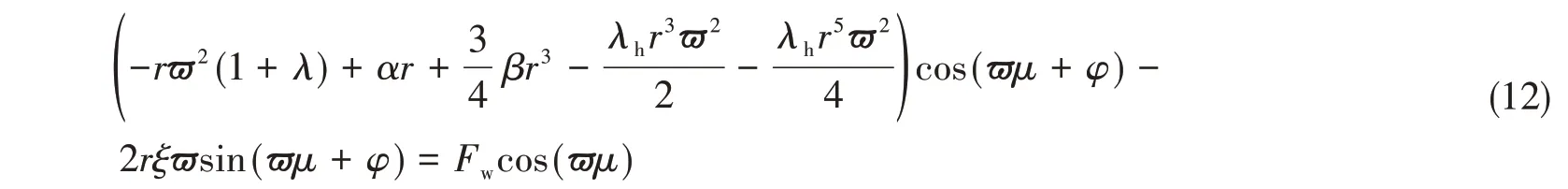
经过数学变换可得

根据三角变换，式（13）可化为

2 数值仿真及分析

2.1 隔振特性分析

根据图3（b）中经典QZS隔振器的动力学模型可知，惯质比λ与λh为0，则式（14）可化为

根据图3（c）中经典ISD隔振器的动力学模型可知

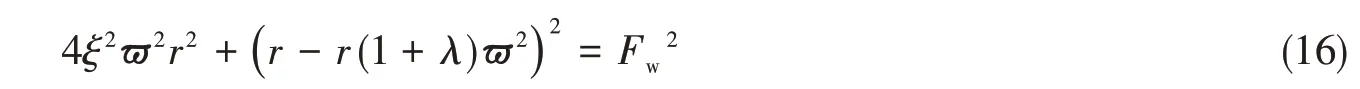
为了分析三种隔振系统的固有特性，令系统中阻尼以及外部激励等于0，则CNI 隔振系统的稳态响应如式（17）所示。

经典QZS隔振系统的稳态响应如式（18）所示。

经典ISD隔振系统的稳态响应如式（19）所示。

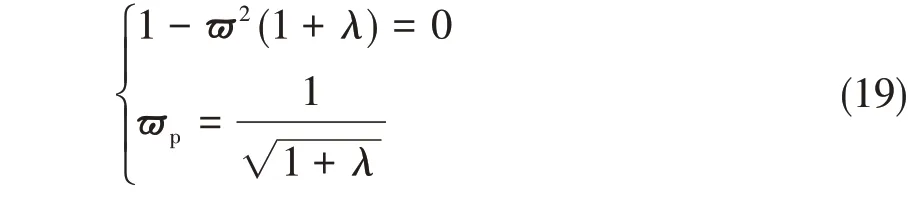
为了更直观地分析各减振系统的稳态响应，将其应用于舰船动力设备的隔振中。5DK-20 柴油发动机组作为我国经典的一款发动机组具有很多的优点，但其在工作过程中扰动扭矩较大，直列式的柴油机相较V列式会产生更大的往复惯性力，基于上述原因其在船舶工程领域上的应用受到了一定的限制。令CNI 隔振系统中α=0，β=2.2，λ=20，λh=20；经典QZS 隔振系统中α=0，β=2.2，λ=0，λh=0；经典ISD 隔振系统中λ=0。将上述参数分别代入各减振系统的稳态响应表达式中，结果如图4所示。

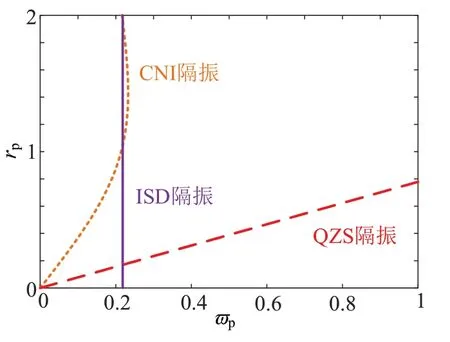
图4 稳态响应曲线Fig.4 Steady-state response curve

图4展示了图3中不同隔振系统的稳态响应曲线。通过观察可以发现，经典QZS隔振系统的稳态响应曲线随着响应频率的增加，其响应幅度也逐渐增加，即响应幅度与响应频率成正比，呈现出曲线硬化的特点；而ISD 隔振系统的稳态响应曲线则是位于低频范围内的一条直线；CNI 隔振系统的稳态响应曲线则结合了二者的特点，响应曲线开始时逐渐向高频方向发展，当其到达某一个拐点时，随着响应幅度rp的增加，曲线逐渐开始向低频方向弯曲。

为了进一步探究CNI 隔振系统稳态响应曲线变化的规律，有必要对其拐点分布作进一步讨论。对式（17）求导可得

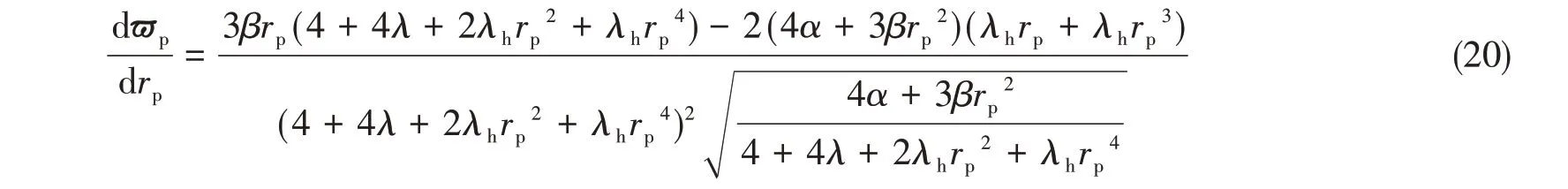
令式（20）等于0，可化简为

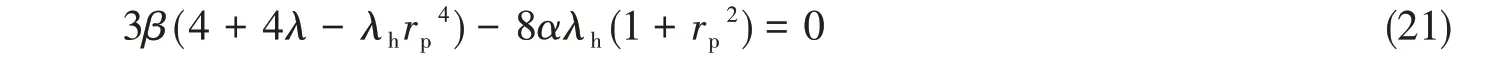
设置CNI 隔振系统参数α=0，β=2.2，λh=15，改变惯质比λ的取值，将其代入式（19）求得拐点，结果如图5（a）所示；令λ=15，改变惯质比λh的取值，结果如图5（b）所示。

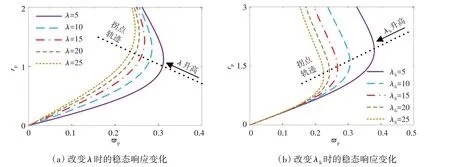
图5 改变惯质比时CNI隔振系统的稳态响应曲线Fig.5 Response of CNI vibration isolation system with the change of inertia ratio

图5 展示了改变惯质比时CNI 隔振系统稳态响应曲线的变化情况以及拐点的运行轨迹。随着惯质比的增大，可以发现响应曲线随着响应幅度rp的增大逐渐向低频方向弯曲；同时通过对式（21）的求解，获得了不同惯质比下的拐点位置，进而得到一条拐点的运行轨迹，可以看出惯质比λ及λh对于拐点运行轨迹的影响是不同的，如图5（a）所示，随着λ的增大，拐点轨迹逐渐上升，而拐点位置则随着频率比ϖp的减小逐渐向幅值rp增大的方向移动；如图5（b）所示，随着λh的增大，拐点轨迹逐渐下降，拐点位置逐渐向频率比ϖp和幅值rp减小的方向移动。这表明通过调整惯质比能够控制响应曲线拐点的位置，进而改变其隔振特性。

为了对系统隔振性能作进一步了解，设定系统参数L=1.3，Fw=0.01，K=3.4，ξ=0.01，λh=20，λ=20。将上述参数代入式（14）～（16）中，可获得不同隔振系统的动力学响应，如图6（a）所示；为了对比不同惯质比下CNI隔振系统的动力学响应，令λ=λh，其余参数不变，响应分析结果如图6（b）所示。

通过图6（a）可以发现，CNI隔振系统在低频阶段具有与QZS 隔振系统类似的硬化刚度特性，而后随着幅值的增加，频率响应曲线逐渐向低频方向弯曲，这是由于惯容器的作用。图6（b）展示了改变惯质比时CNI 隔振系统的动力学响应，随着惯质比的增大，共振峰值逐渐向低频方向移动，即惯质比的增大扩大了CNI隔振系统的有效频率范围，并且惯质比主要对共振峰区域产生影响，而对远离共振区的频率段几乎没有影响。同时可以观察到惯容器的引入增大了隔振带宽，但也不可避免地增加了共振峰的幅值。

图6 隔振系统的动力学响应Fig.6 Dynamic response of the vibration isolation system

对比图3（b）与图3（c）中隔振系统的结构，发现CNI隔振系统增加了横向弹簧，因此有必要研究横向弹簧刚度对隔振系统响应特性的影响，设置刚度比K分别为0（α=1，β=0）；0.5（α=0.85，β=0.325）；1（α=0.7，β=0.65）；1.5（α=0.55，β=0.975）；2（α=0.4，β=1.3），其他参数ξ=0.01，F=0.01，L=1.3，λ=20，λh=20。

图7展示了改变横向弹簧刚度时不同隔振系统响应曲线的变化情况，图7（a）为CNI隔振系统的响应曲线，可以看出当刚度比K为0 时，响应峰曲线逐渐向低频方向弯曲，随着弹簧刚度的增大，曲线共振峰逐渐向低频方向移动，而其曲线峰值则逐渐偏向高频方向。观察图7（b）可发现当K等于0时，曲线共振峰所处位置频率较高，且峰值曲线近似为直线；随着刚度K的增加，共振峰逐渐向低频方向偏移，峰值曲线则向高频弯曲；对比可以看出加入惯容器后会改变系统峰值曲线的弯曲方向。

图7 横向弹簧刚度对隔振特性的影响Fig.7 Influence of lateral spring stiffness on vibration isolation characteristics

2.2 系统稳定性分析

在实际工程应用中，系统的稳定与否直接决定了工程的成败。对于线性系统来说，绝大多数的运动都是稳定的，但对于非线性系统而言则未必如此[16]，因此有必要对本文所述的非线性振动系统进行稳定性方面的分析。

对于非线性振动系统来说，为了简化计算，可以利用一次近似判别法来对系统的稳定性进行判别。对于该系统有

将其概念一般化，利用状态向量[x1x2]对其变量[x ẋ ]进行替换，即可化为

非线性系统中可以有多个平衡位置，但并非所有的平衡位置均是稳定的，因此需要确定出该系统所有的平衡位置，进而对其进行辨别。平衡的条件可以表示为

在平衡点邻域内将式（23）按泰勒公式展开，则可表示为

此时非线性系统可以表示为

与之相对应的一次近似系统为

为了分析本文所提非线性隔振系统的稳定性，将式（8）进行变换可得

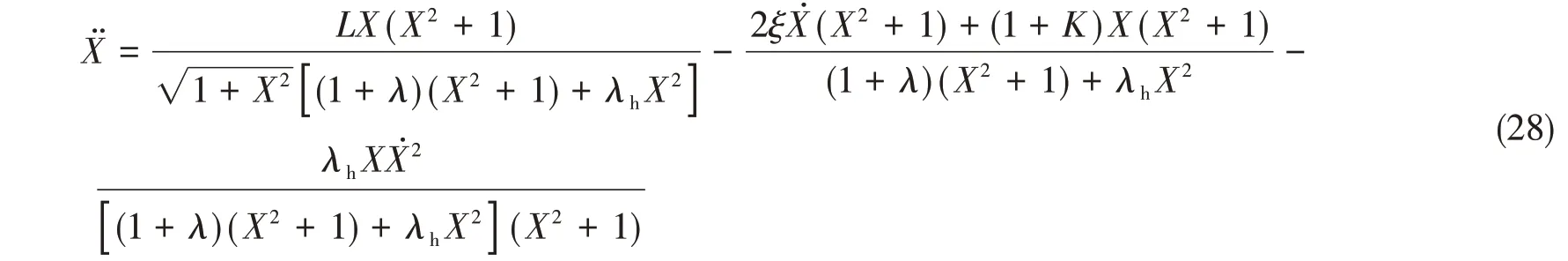
利用状态向量[x1x2]对式(28)中变量[X]进行替换，新的表达式为

依据式（24）对系统的平衡点进行求解，可获得该系统的平衡位置为

在该平衡位置将其展开为泰勒级数并简化，则式（29）可表示为

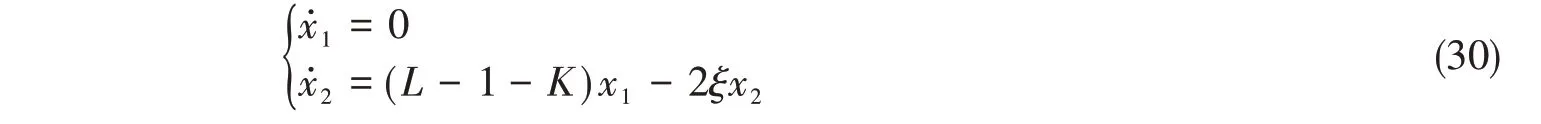
系数矩阵为

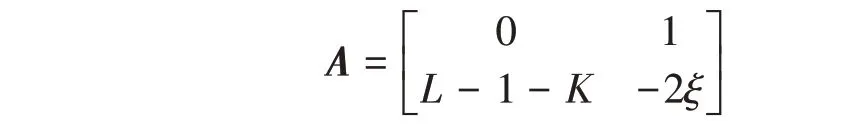
特征方程的系数为

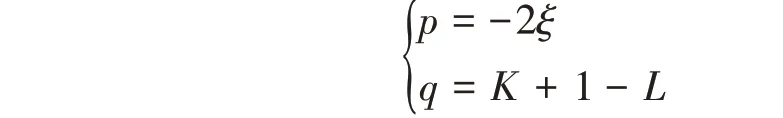
将系统参数L=1.3，K=3.4，ξ=0.01代入并计算判别式，可得

按照一次近似判别法可认定该系统是稳定的。

2.3 力传递特性分析

力传递率在隔振器的评估体系中占有重要地位，通过计算观测力传递率的大小即可判定隔振器的隔振性能。

根据系统动力学方程可知，忽略其高阶频率处的分量，CNI隔振系统传递到上层的力可近似为

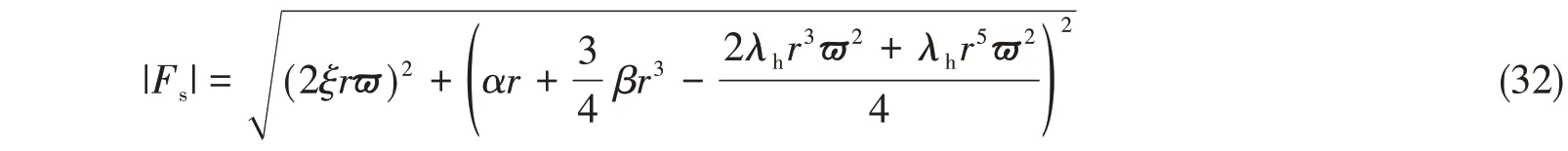
将传递力与激励的比值定义为力传递率T，则CNI隔振系统的力传递率可表示为

令参数ξ=0.01，F=0.01，K=3.4，L=1.3，将参数代入式（21）可获得该系统的力传递特性，改变惯质比λ的数值（λh=20），并基于谐波平衡法对系统进行求解，最终的力传递曲线的数值结果如图8（a）所示；改变惯质比λh的数值（λ=20），基于谐波平衡法对系统求解，数值结果如图8（b）所示；同时改变惯质比λ和λh的值（λ=λh），对系统进行求解，结果如图8（c）所示。如图8（a）中放大图所示，随着惯质比λh的增大，系统力传递率的大小基本保持不变，但曲线逐渐向低频方向移动；而改变λ时，可以发现系统的有效频率范围会随之发生改变；图8（c）展示了同时改变惯质比λ和λh时系统的力传递变化，观察发现当惯质比数值较小时，其与经典QZS 隔振系统的力传递特性类似，曲线逐渐向高频方向扩展；随着惯质比的增大，向高频方向弯曲的趋势逐渐减弱，且出现低频回转的现象。这些特性进一步证明了CNI隔振系统能够有效改善系统的隔振带宽，增大有效使用范围。同时与混合船舶动力隔振系统［17］相比，本文CNI隔振系统结构简单，未引入外部能量，并且系统能够通过改变惯质比进而控制系统的隔振特性，提供更宽的隔振频带。

图8 CNI隔振系统的力传递率Fig.8 Force transmission rate of CNI vibration isolation system

3 结 论

本文提出一种可提升低频隔振效果的的舰船CNI隔振系统，该隔振系统由横向惯容器、横向弹簧以及经典ISD 隔振器组合而成。基于谐波平衡法获得该系统的频率响应关系和力传递特性，并与经典ISD隔振器以及经典QZS隔振器进行对比，研究发现：（1）CNI隔振系统的频率响应曲线更倾向于低频方向弯曲，且相较于其他隔振器，有着更小的响应峰值；（2）随着惯质比λ的增大，隔振系统的动态响应幅值逐渐增大，并且力传递率的频带更宽，有效范围更大。

研究结果表明，该CNI隔振系统有着更好的低频隔振性能，这些发现有助于进一步了解非线性惯容隔振系统的动态特性，并且为舰船隔振系统的设计提供了新的思路。