沙柳力学性能试验及数值模拟1)
张少勇 刘志刚 裴承慧 段明泽 王淼 田丰
(内蒙古工业大学,呼和浩特,010051)
沙柳(Salixpsammophila)是我国西北地区防风固沙的主要树种,具有平茬复壮的生物习性,即到达一定生长年限需要对其进行平茬处理,否则会出现生长缓慢甚至枯死的现象。目前主要的平茬机具为圆锯片式割灌机,在实际平茬作业时出现功耗大、刀具发热严重、茬口灼伤、撕皮撕裂等现象,这些问题主要是刀具结构不合理和工作参数不匹配导致。研究沙柳力学性能,可以为平茬刀具结构设计和工作参数设定提供数据支持。
沙柳属于小径级灌木,由于其结构的复杂性,表现出正交各向异性材料特性。宏观结构有3个方向:轴向(L)、径向(R)、弦向(T),不同方向物理力学性能存在明显差异。对于同一根沙柳,不同部位的含水率不相同,而含水率会导致物理力学性能不同[1];此外,温度也会影响沙柳物理力学性能[2]。
关于木材相关力学性能的测定都有相应的测试标准,已有较多相关树种和木制产品的准静态物理力学特性研究成果[3-7],并且通过数值模拟方法研究木质结构力学特性[8-13],但对模拟过程计算方法研究较少。为此,本研究以一定含水率和温度的沙柳作为试验对象,通过准静态力学试验测定其强度参数,并依据LS-DYNA建立与试验原理相同的有限元模型,采用隐式自动切换显式算法进行拉伸、压缩、剪切试验,测定沙柳同一部位在温度和含水率一定时不同方向上的力学性能。旨在为沙柳的切削仿真研究提供参考。
1 材料与方法
1.1 试验材料
研究区位于内蒙古自治区鄂尔多斯市准格尔旗十二连城乡(40°12′~40°21′N,110°59′~111°20′E),海拔1 018~1 109 m。选用11月份处于平茬期的沙柳(Salixpsammophila);由于沙柳不同部位的含水率有很大差异,且含水率对沙柳的力学性能影响较大,所以选择健康生长、枝条通直、无侧条等缺陷的膝径大于12 mm的沙柳,并截取其平茬部位作为试验材料,样本数为15,经测定试验材料含水率为37.49%、密度为637.52 kg/m3,试验温度为20 ℃。
1.2 沙柳力学性能测试试验方法
应用WDW-T100微机控制电子万能试验机,参照GB/T 1938—2009《木材顺纹抗拉强度试验方法》、GB/T 14017—2009《木材横纹抗拉强度试验方法》、LY/T 2369—2014《沙生灌木物理力学性能测试方法》,测试抗拉强度;参照GB/T 1935—2009《木材顺纹抗压强度试验方法》、GB/T 1939—2009《木材横纹抗压试验方法》、LY/T 2369—2014《沙生灌木物理力学性能测试方法》,测试抗压强度;参照LY/T 2369—2014《沙生灌木物理力学性能测试方法》,测试抗剪强度。
1.3 沙柳力学性能测试试验的数值模拟方法
采用LS-DYNA中*MAT143_WOOD作为沙柳的材料模型。由电测法试验测得沙柳的弹性常数:其中顺纹弹性模量为9531 MPa、横纹弹性模量为722 MPa、顺纹剪切模量为385 MPa、横纹剪切模量为142 MPa、泊松比为0.454。由准静态强度试验测的沙柳的5种强度:其中顺纹抗拉强度为82.625 MPa、顺纹抗压强度为28.290 MPa、横纹抗拉强度为6.949 MPa、横纹抗压强度为4.599 MPa、顺纹抗剪强度为5.858 MPa。
依据LS-DYNA建立与试样尺寸相同的有限元模型。由于5种强度试验均为准静态试验,且试验过程中沙柳会经历弹性、塑性、失效3个阶段,故数值模拟时,若只采用显式方法,由于试验时间很长,会极大增加计算成本,若只采用隐式方法,当模拟至材料失效阶段会出现计算不收敛。故沙柳准静态试验数值模拟采用隐式自动切换显式的方法进行,在线弹性阶段可以采用大的时间步,减少计算时间,当出现隐式计算不收敛时,会自动切换为显式计算,以模拟材料的失效阶段,以此研究沙柳在拉伸、压缩和剪切中的应变分布和破坏机理。
1.4 沙柳力学性能测试试验模拟模型的构建
依据LS-DYNA建立与试样尺寸、试验原理相同的有限元模型(见图1),其中拉伸和压缩有顺纹和横纹2种模型,剪切只有顺纹模型。试验材料模型均为*MAT143_WOOD,压板和固定板均为刚体。选用Solid164实体单元,采用隐式自动切换显式算法进行,具体通过关键字*IMPLICIT_AUTO、*IMPLICIT_DYNAMICS、*IMPLICIT_GENERAL、*IMPLICIT_SOLIUTION实现。单元尺寸为1 mm;沙漏控制类型为4、系数为0.1;压缩和剪切试验中,刚体与沙柳的接触方式为*AUTOMATIC_SURFACE_TO_SURFACE,动静摩擦系数分别为0.2、0.4。通过关键字*ASCII_OPTION中接触面反作用力(RCFORC)可得到模拟过程中的相互作用力;拉伸试验中只有一个体无相互作用力,后处理中分别用断裂面上单元的应力和加载面上单元的位移即可得到应力-位移曲线。所有试验都是准静态试验,故在模拟中不考虑应变率对沙柳强度的影响。

图1 拉伸、压缩和剪切有限元模型
2 结果与分析
2.1 沙柳强度测试试验结果
沙柳的顺纹抗拉强度是指沿木材纹理承受载荷的最大能力,试验时沿着纹理方向进行单轴拉伸。沙柳的顺纹拉伸破坏形式,主要是纵向的撕裂粗纤维和微纤丝之间的剪切,而非纤丝的断裂,故断口参差不齐。试验中整体位移为1.03 mm,延伸率很小,当载荷达到1.322 kN时试件破坏,求得沙柳的顺纹抗拉强度为82.625 MPa。由图2可见:沙柳的载荷和位移呈线性关系,当强度达到82.625 MPa时开始进入塑性阶段,位移在1.024 mm到1.03 mm之间即曲线第Ⅱ段,所以沙柳的顺纹拉伸在破坏前变形很小,属于脆性破坏。
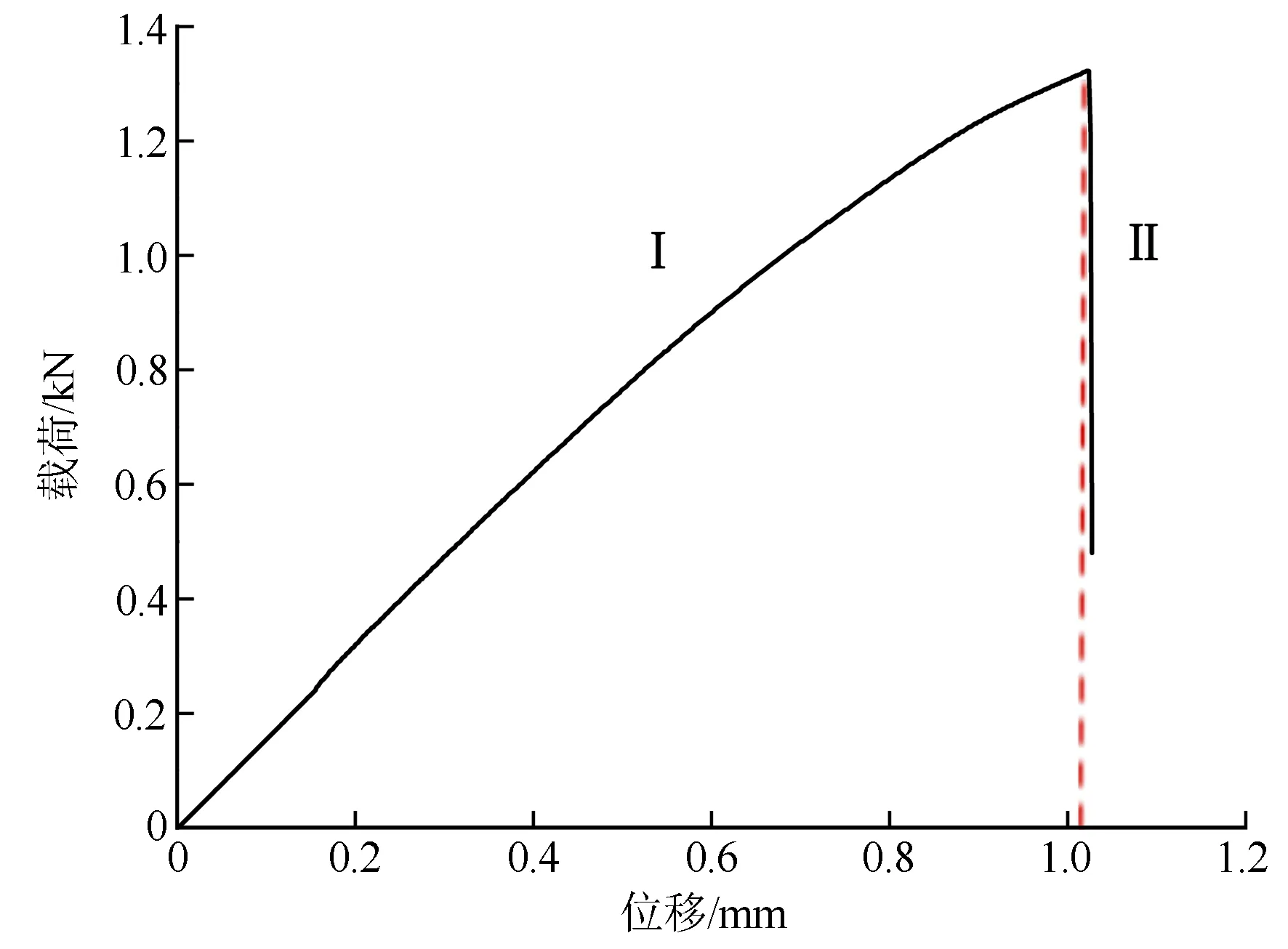
图2 沙柳顺纹拉伸载荷-位移曲线
横纹拉伸分径向拉伸和弦向拉伸,本研究试验选择弦向拉伸试件,测定沙柳的横纹抗拉强度。横纹拉伸的破坏形式为木纤丝之间非结晶物质(半纤维素、木质素和果胶)的破坏,断裂口较为平整。由图3可见:破环时载荷为0.521 kN,结合破坏截面面积得到沙柳横纹抗拉强度为6.949 MPa,载荷和位移呈线性关系且变形很小,属于脆性破坏。
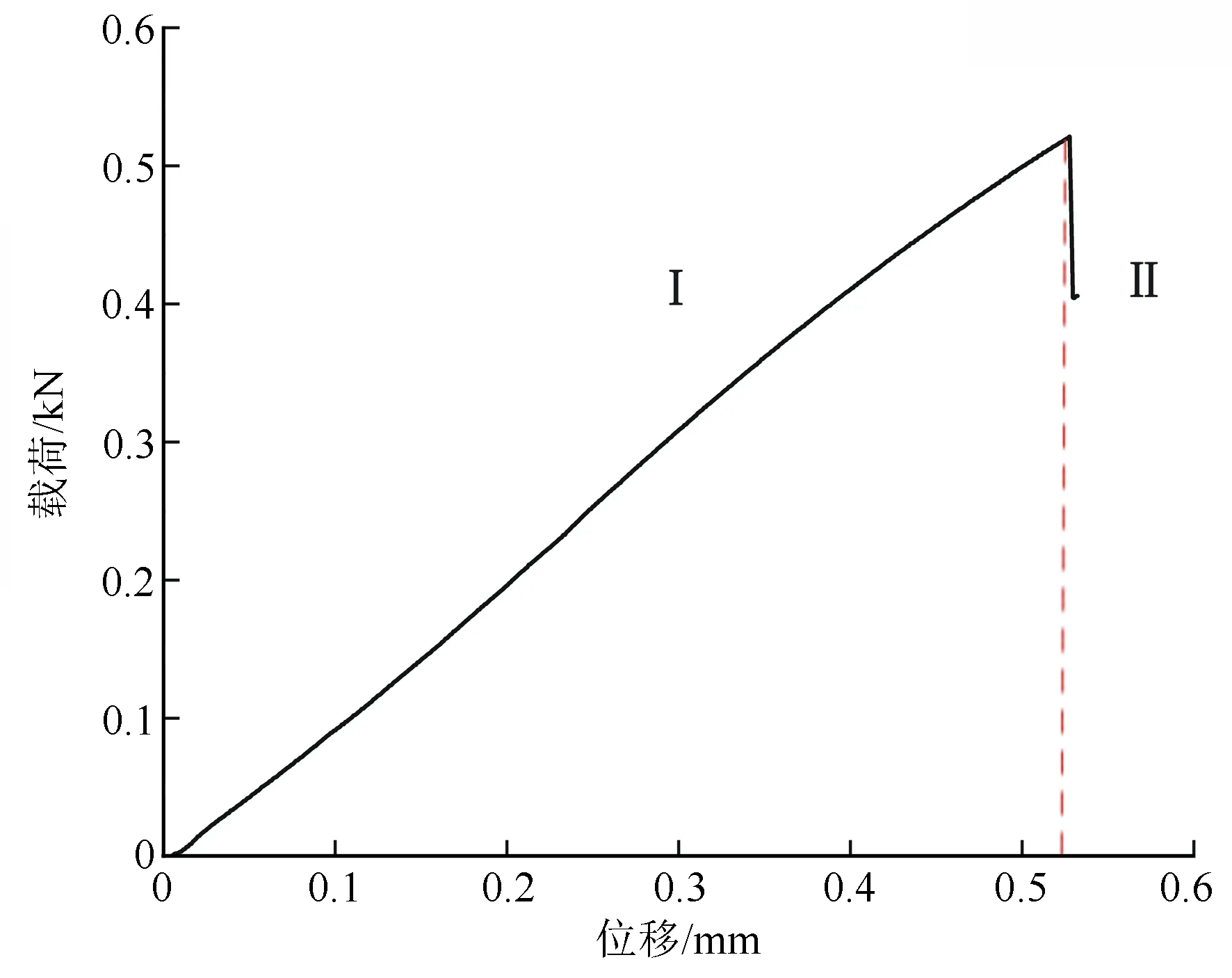
图3 沙柳横纹拉伸载荷-位移曲线
抗压强度是当沙柳在受到单轴压力时,能抵抗外力压缩变形的能力。沙柳顺纹受压破坏是木材细胞壁失稳的结果,而非木纤丝的断裂。由图4可见:载荷-位移曲线有明显的线性阶段(弹性阶段,位移从0到1.651 mm)和非线性阶段(塑性阶段,位移从1.651 mm到2.577 mm),即曲线中第Ⅰ段和第Ⅱ、Ⅲ段;其中,比例极限载荷为2.44 kN、破坏载荷为2.83 kN,求得沙柳屈服强度为24.447 MPa、极限强度为28.290 MPa。沙柳的顺纹压缩破坏前,位移在1.651 mm到2.123 mm有明显的塑性阶段,即曲线第Ⅱ段,属于延性破坏。
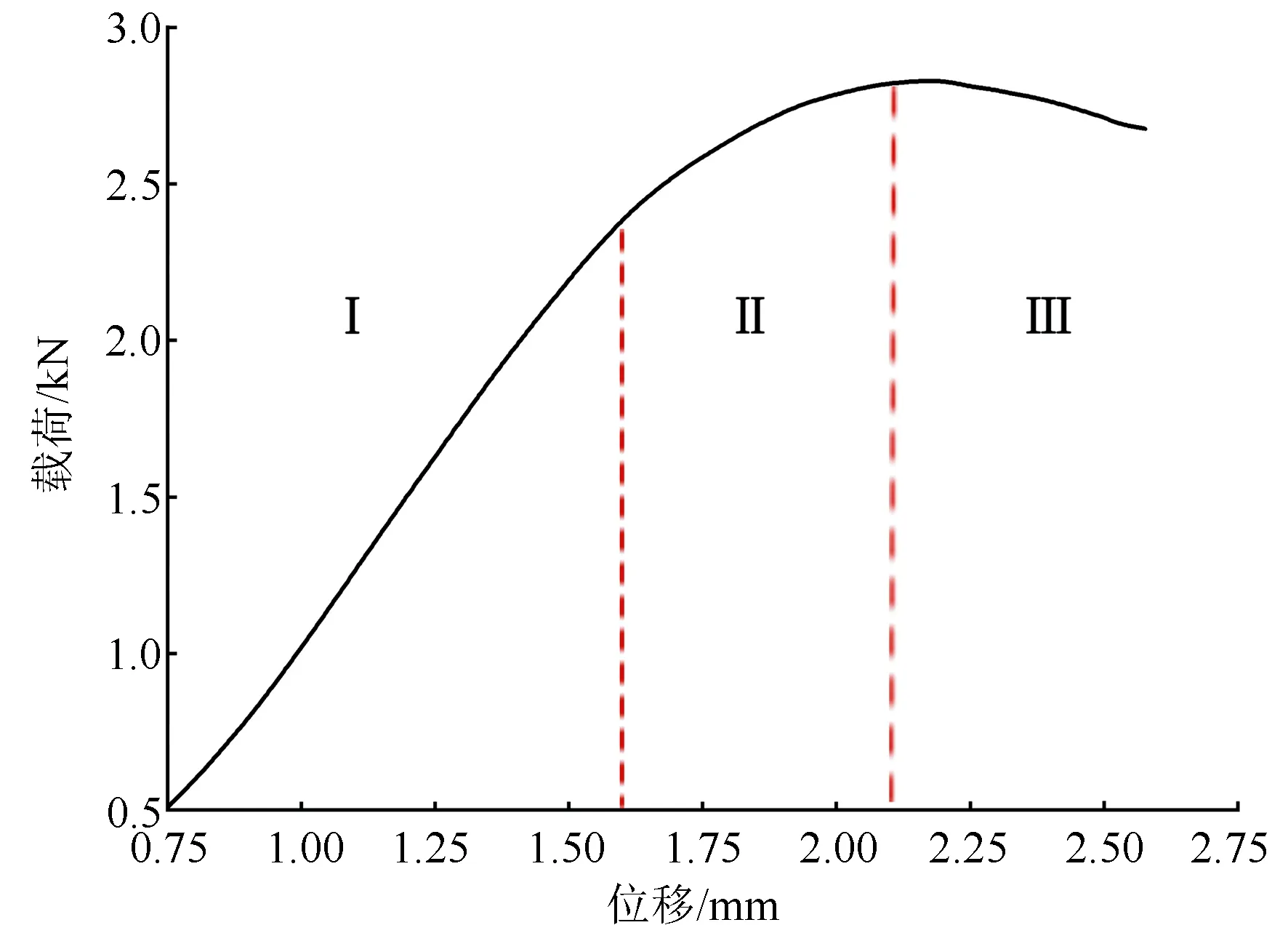
图4 沙柳顺纹压缩载荷-位移曲线
横纹压缩包括径向压缩和弦向压缩,本研究试验选择弦向压缩,测定沙柳的横纹抗压强度。由图5可见:横纹压缩的载荷-位移是一条非线性曲线,开始为弹性阶段,载荷与位移呈线性关系,比例极限载荷为0.25 kN,得出屈服强度为2.493 MPa;随着载荷的增加,越过比例极限之后,细胞壁被压溃发生腔内坍塌,导致载荷增量小而位移增量大,该阶段为塑性屈曲(也成为应力平台)[14],极限强度为4.599 MPa;随着载荷继续增加,细胞壁腔被完全填充、细胞壁相互接触,导致载荷的增量大而位移增量小。沙柳的横纹压缩有明显的塑性阶段,属于延性破坏。

图5 沙柳横纹压缩载荷-位移曲线
木材的抗剪强度分为顺纹剪切和横纹剪切,实际应用中横纹剪切十分罕见,而且由于横纹压缩强度很小,在横纹剪切时总是会先出现局部压缩失效,导致木纤丝发生拉伸作用而非单纯的剪切破坏,故通常不作为木材的力学性能指标,通常横纹抗剪强度为顺纹抗剪强度的3~4倍[15]。沙柳顺纹抗剪强度为抵抗剪切应力的最大能力,破坏特点是木纤丝在平行纹理的方向上发生相对滑移。由图6可见:沙柳顺纹抗剪试验中,载荷-位移由非线性关系转变为线性关系,破坏时载荷为1.757 kN,得出沙柳抗剪强度为5.858 MPa。沙柳材的顺纹剪切无明显塑性阶段,属于脆性破坏。
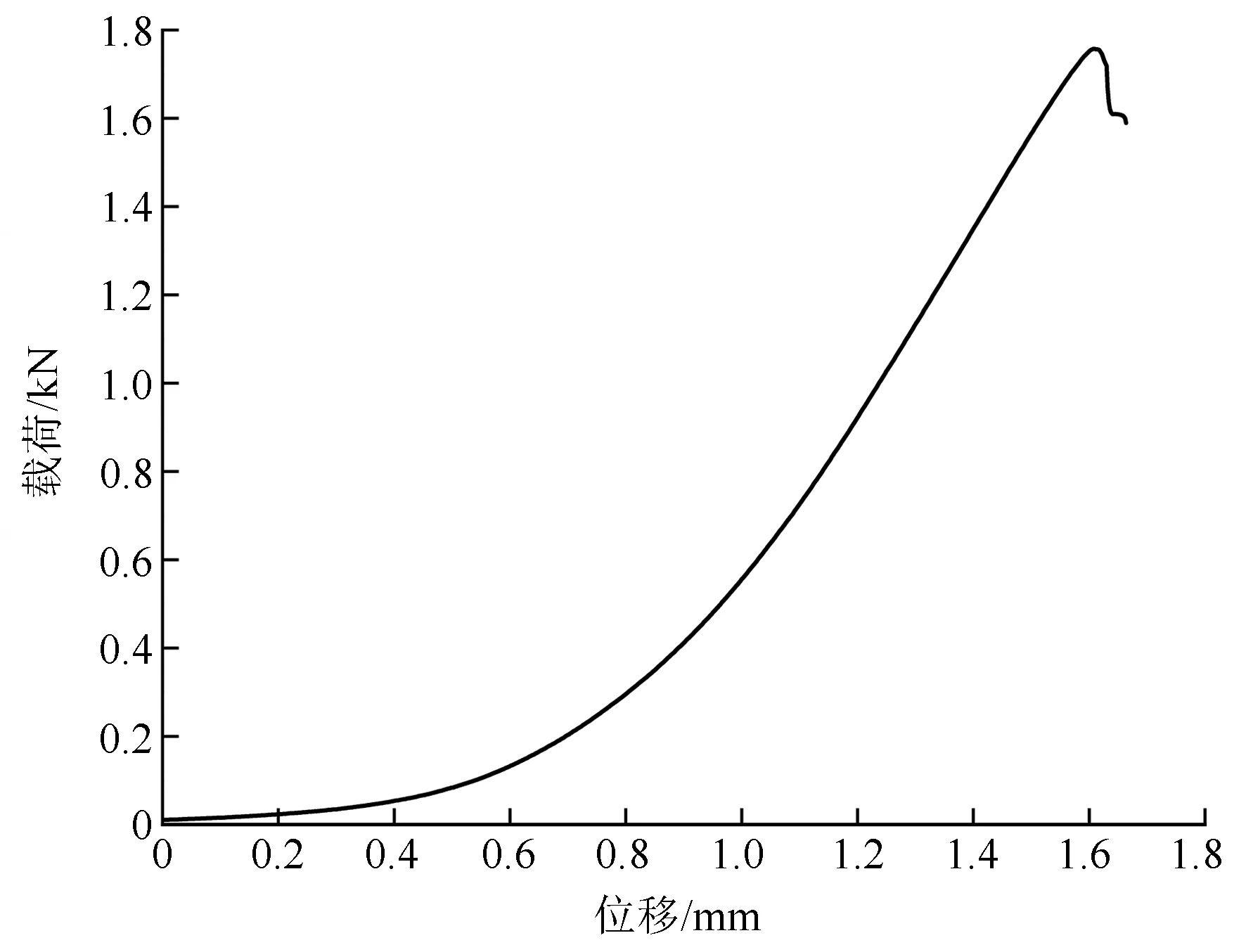
图6 沙柳顺纹剪切载荷-位移曲线
2.2 沙柳强度测试试验的数值模拟
2.2.1 沙柳拉伸试验的数值模拟
数值模拟中沙柳顺纹试件和横纹试件断裂情况不同(见图7)。沙柳的顺纹拉伸破坏形式,主要是纵向撕裂粗纤维和微纤丝之间的剪切,而非纤丝的断裂。由图7可见:断口不平整,端口处的不同单元层相互交错,单元呈“平行四边形”状是拉伸过程中发生单元间相互剪切造成的;横纹拉伸中,失效形式为木纤丝之间填充物的破坏,填充物为非结晶物质,包含半纤维素、木质素、果胶等[15],故断口较为平齐。二者破坏形式与试验试件失效形式相符。

图7 沙柳顺纹、横纹拉伸模拟试验失效状态
位移-应力与载荷-位移性质相同,沙柳拉伸破坏是脆性的,达到失效强度之后载荷会瞬间卸载,拉伸试验中位移-载荷曲线整体呈线性关系,特别是在顺纹拉伸末尾出现了短暂的塑性变形,而数值模拟过程中材料失效前位移-应力为严格的线弹性关系,斜率与沙柳的弹性模量相关。沙柳的顺纹拉伸强度为82.625 MPa,数值模拟断裂处应力为80.861 MPa(见图8),二者相差2.1%;横纹拉伸强度为6.949 MPa,数值模拟断裂处的应力为6.637 MPa(见图8),二者相差4.5%。数值模拟与试验结果基本相符。
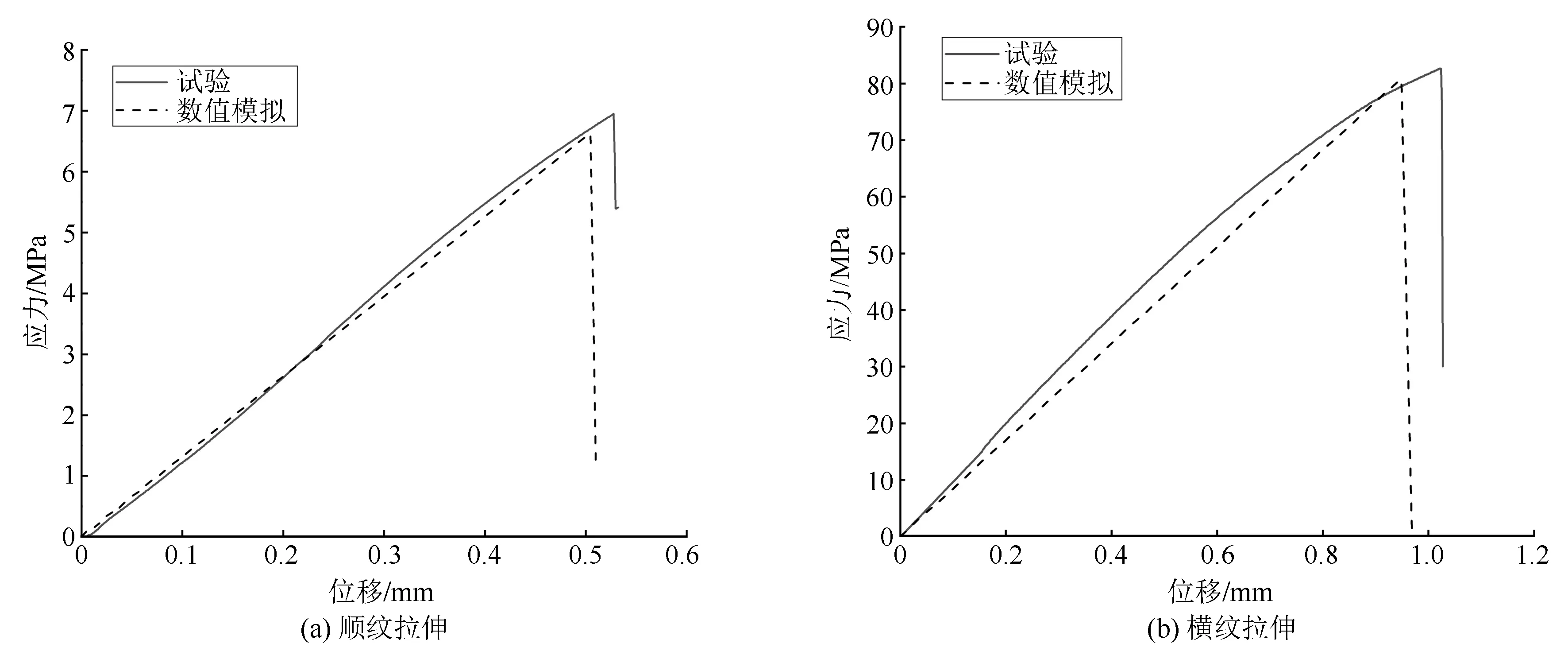
图8 沙柳顺纹、横纹拉伸模拟试验位移-应力曲线
2.2.2 沙柳压缩试验的数值模拟
由图9可见:顺纹压缩中,最大等效应变发生在试件顶部和底部,中部等效应变较为均匀;压缩模拟中,等效应变结果符合试验中试件顶部和底部变形较为明显的特征。横纹压缩中,最大等效应变云图整体呈“沙漏”状,最大应变发生在试件中部两侧的位置,与试验中试件的变形结果相符。

图9 沙柳顺纹、横纹压缩等效应变云图
由图10可见:沙柳顺纹和横纹的压缩试验中有明显的弹性和塑性阶段,弹性阶段与数值模拟结果相符;随着载荷增加进入塑性阶段,顺纹压缩与横纹压缩表现出不同的塑性变化,但是对于数值模拟,由于*MAT143_WOOD模型对木材压缩过程中没有引入损伤积累,故当载荷达到强度极限之后并无卸载,而是保持恒定应力用以表示塑性阶段。顺纹压缩数值模拟优于横纹压缩。图5和图10(b)中,横坐标位移取值范围不同,这是由于数值模拟中无法表征实际试验中沙柳达到破坏极限以后,细胞壁腔被完全填充,承载能力增强的过程;所以图10(b)中只对比了从加载开始到达到破坏极限这一阶段。
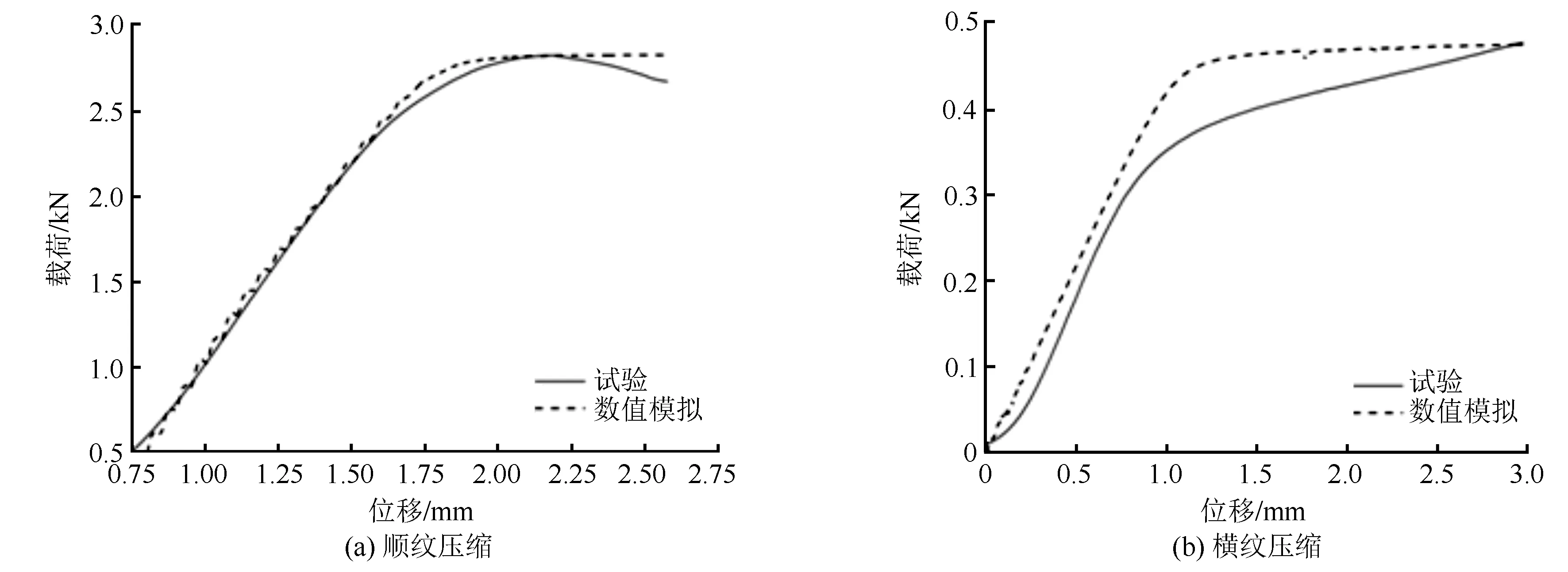
图10 沙柳顺纹、横纹压缩载荷-位移曲线
2.2.3 沙柳剪切试验的数值模拟
由图11可见:剪切失效位置与顺纹剪切试验结果相符,应变主要集中在受剪部位,且最大应变出现在试件剪切面上端。这是由于试件顶端受载面,随着载荷的增加右侧应变逐渐大于左侧应变,致使剪切过程中会出现y向载荷分量。
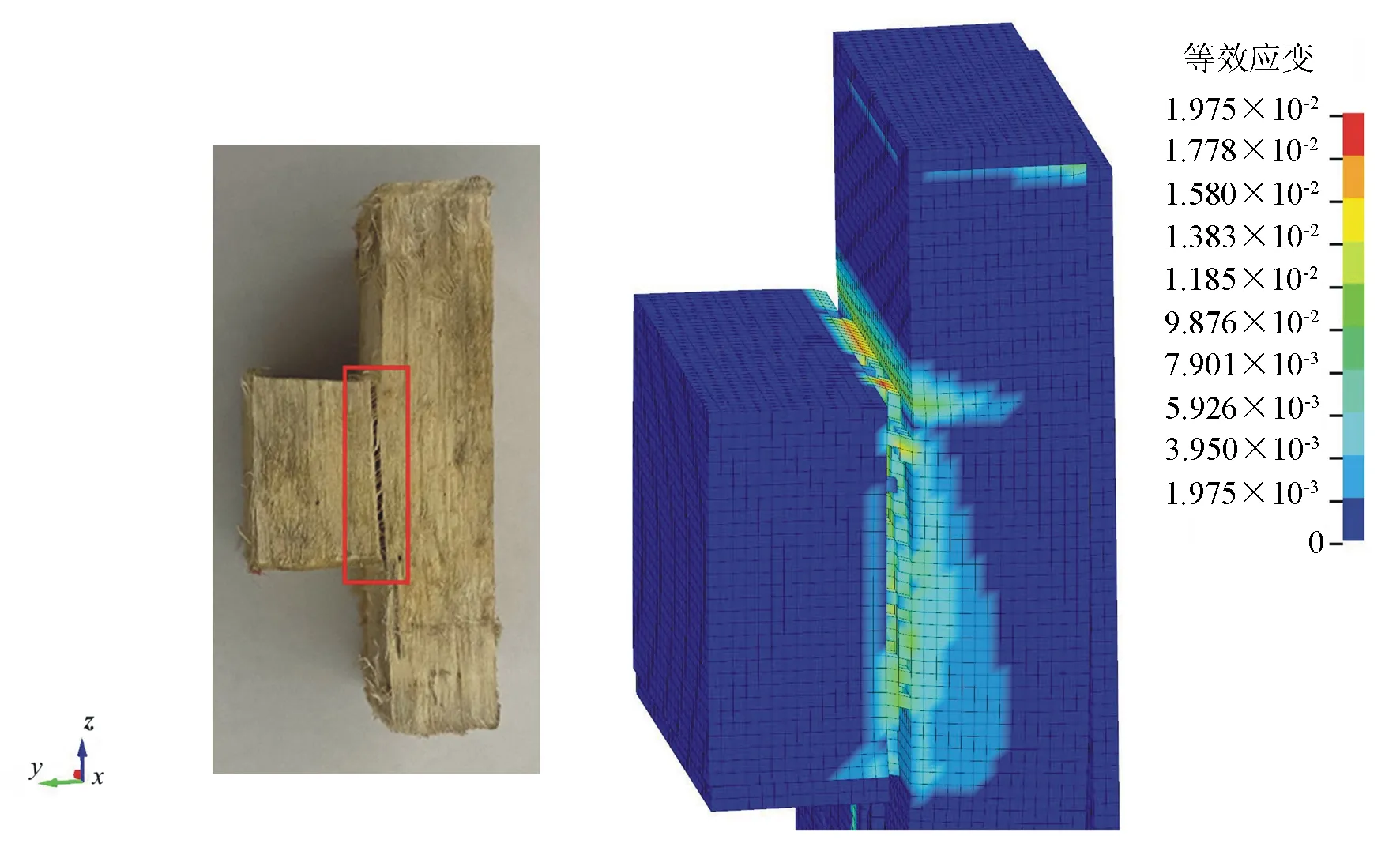
图11 沙柳顺纹剪切失效时等效应变云图
由图12可见:图中二者整体趋势接近,受试件制作精度影响,加载初期试件表面并非完全受载,使得试验曲线的前段会出现一段平缓区域。比对结果与试验结果相同,数值模拟中,顺纹剪切破坏是脆性的,且载荷-位移也是由非线性阶段过渡至线性阶段;顺纹抗剪强度为5.858 MPa,所对应载荷为1.757 kN,数值模拟失效时载荷为1.728 kN,二者相差1.7%。数值模拟结果与试验相符。

图12 沙柳顺纹剪切位移-载荷曲线
3 结论
通过强度试验,测得沙柳顺纹和横纹方向上的拉伸、压缩强度及顺纹方向上的剪切强度。结果表明:①顺纹的抗拉强度为82.625 MPa,约为顺纹抗压强度的3倍;横纹抗拉强度为6.949 MPa,约为顺纹抗压强度的1/4;横纹抗压强度为4.599 MPa,约为顺纹抗压强度的1/6;顺纹抗剪强度为5.858 MPa,约为顺纹抗压强度的1/5;均符合木材各向强度之间的关系。②沙柳在受拉和受剪中表现为脆性破坏,受压中表现为延性破坏。
依据LS-DYNA对沙柳所有准静态试验进行数值模拟,数值模拟过程采用与试验原理相同的有限元模型。计算结果表明:①在拉伸和剪切试验模拟中,试件的破坏形式与试验结果一致,数值模拟拉伸时应力-位移曲线与剪切时载荷-位移曲线基本一致,极限载荷较为接近,相差均在5%之内。②压缩试验的模拟结果中曲线趋势劣于拉伸和剪切试验,但对沙柳在压缩中表现出的弹塑性阶段均有体现,且压缩强度极限值基本吻合。验证了LS-DYNA用于模拟木材准静态试验的可行性,为应用LS-DYNA对沙柳切削仿真提供参考。

