对一道课本习题的探讨

项当

三角形求角度问题形式众多，笔者认为，在平时的学习中，不仅要重视教材本身知识，还要学会变通，会将间接条件转化为直接条件，并加以归纳应用，教学中重视对例题和习题的“改装”或引申，把分散的知识点串成一条线，最大可能地覆盖知识点，有利于知识的建构.

1 原题呈现

如图1，D是AB上一点，E是AC上一点，BE，CD相交于点F，∠A=62°，∠ACD=35°，∠ABE=20°.求∠BDC和∠BFC的度数.

解 在△ACD中，

因为∠A=62°，

∠ACD=35°，

所以∠BDC=∠A+∠ACD

=62°+35°

=97°;

在△BDF中，

∠BFC=∠BDC+∠ABE

=97°+20°

=117°.

2 变式探究

变式1 如图2，D是AB上一点，E是AC上一点，BE，CD相交于点F，∠A=62°，CD⊥AB，BE⊥AC，求∠BFC的度数.

解 因为CD⊥AB，

所以∠ADC=∠BDC=90°，

因为BE⊥AC，

所以∠AEB=∠CEB=90°，

在△ABE中，

∠ABE=180°-∠A-∠AEB=28°，

在△BDF中，

∠BFC=∠BDC+∠ABE

=90°+28°

=118°.

变式2如图3，D是AB上一点，E是AC上一点，BE，CD相交于点F，∠A=62°，CD平分∠ACB，BE平分∠ABC，求∠BFC的度数.

解 因为CD是∠ACB的平分线，

所以∠ACD=∠BCD=12∠ACB，

因为BE是∠ABC的平分线，

所以∠ABE=∠CBE=12∠ABC.

在△ABE中，

∠BEC=∠A+∠ABE，

在△ECF中，∠BFC=∠BEC+∠ACD，

所以∠BFC=∠A+∠ABE+∠ACD

=∠A+12∠ABC+12∠ACB

=∠A+12（∠ABC+∠ACB）

=∠A+12（180°-∠A）

=90°+12∠A

=121°.

变式3 如图4，D是AB上一点，E是AC上一点，BE，CD相交于点F，CD⊥AB，BE平分∠ABC，∠ABE=23°，求∠CFE的度数.

解 因为CD⊥AB，

所以∠BDC=∠ADC=90°，

在△BDF中，

∠BFD=180°-∠ABE-∠BDC

=180°-23°-90°

=67°.

所以∠CFE=∠BFD=67°.

变式4 如图5，D是AB上一点，E是AC上一点，BE，CD相交于点F，∠A=62°，∠BDC=98°，BE平分∠ABC，∠DCB=12∠ACD，求∠BFC的度数.

解 在△ADC中，

∠ACD=∠BDC-∠A=98°-62°=36°，

因为∠DCB=12∠ACD，

所以∠DCB=18°，∠ACB=54°，

在△BDC中，

∠ABC=180°-∠A-∠ACB=64°，

因为BE平分∠ABC，

所以∠ABE=∠CBE=12∠ABC=32°，

在△BDF中，

∠BFC=∠BDC+∠ABE=98°+32=130°.

變式5 如图6，D是AB上一点，E是AC上一点，∠BDC=∠ACB，BE平分∠ABC，BE，CD相交于点F，∠ACD=22°，求∠CFE的度数.

解 因为

∠BDC=∠ACB，

设∠ACB=x，∠BDC=x，

在△ACD中，∠A=∠BDC-22°=x-22°，

在△ABC中，∠ABC=180°-∠A-∠ACB

=202°-2x，

因为BE平分∠ABC，

所以∠ABE=∠EBC=101°-x，

在△BDF中，

∠DFB=180°-∠BDC-∠ABE

=180°-x-（101°-x）

=79°，

所以∠CFE=∠DFB=79°.

变式6 如图7，D是AB上一点，E是AC上一点，BE，CD相交于点F，∠A=60°，CD平分∠ACB，BE平分∠ABC，BE=CE+BD，求∠ABC的度数.

解 如图8，在BC上截取BH，使得BD=BH，因为CD是∠ACB的平分线，

所以∠ACD=∠BCD=12 ∠ACB，

因为BE是∠ABC的平分线，

所以∠ABE=∠CBE=12∠ABC，

∠BFC=∠A+∠ABE+∠ACD

=∠A+12∠ABC+12∠ACB

=∠A+12（∠ABC+∠ACB）

=∠A+12（180°-∠A）

=90°+12∠A

=120°，

所以∠DFB=∠EFC=60°.

在△BDF和△BHF中，

BD=BH，∠DBF=∠HBF，BF=BF，

所以△BDF≌△BHF（SAS），

∠DFB=∠BFH=60°，

于是∠HFC=∠EFC=60°，

在△EFC和△HFC中，

∠HFC=∠EFC，FC=FC，∠HCF=∠ECF，

所以△EFC≌△HFC（SAS），

CE=CH，

BC=CH+BH=CE+BD，

所以BC=BE，∠BEC=∠BCE，

设∠ABE=x，

∠BEC=∠BCE=60°+x，

在△ABC中，

∠A+∠ABC+∠ACB=180°，

60°+2x+60°+x=180°，

x=20°，

∠ABC=2x=40°.

变式7 如图9，在Rt△BDC中，∠BDC=90°，DB=DC，F是DC上任意一点，CE与BF的延长线相交于点E，∠ECF=∠DBF，连接DE，求∠DEB的度数.

0

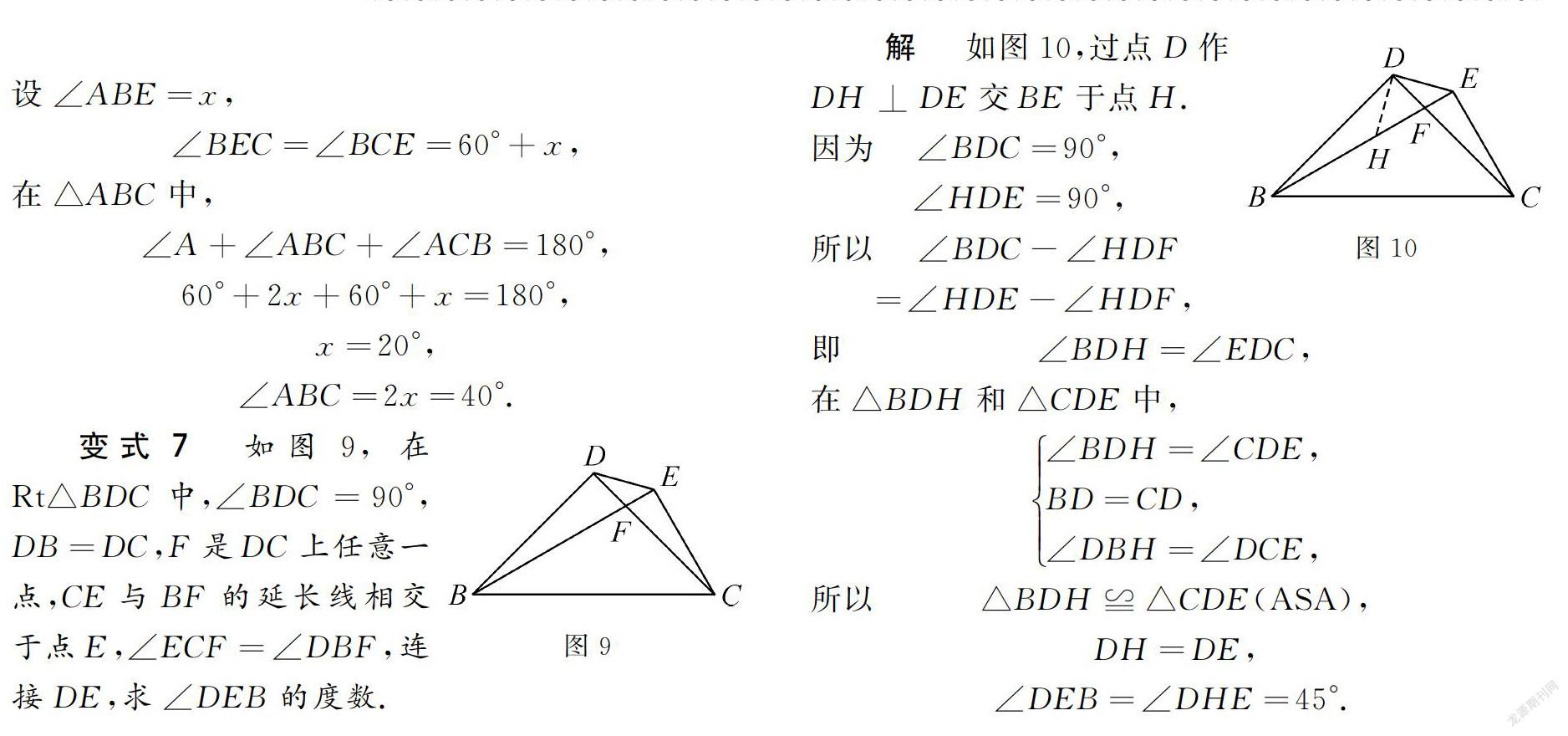
解 如图10，过点D作DH⊥DE交BE于点H.

因为∠BDC=90°，

∠HDE=90°，

所以 ∠BDC-∠HDF

=∠HDE-∠HDF，

即∠BDH=∠EDC，

在△BDH和△CDE中，

∠BDH=∠CDE，BD=CD，∠DBH=∠DCE，

所以△BDH≌△CDE（ASA），

DH=DE，

∠DEB=∠DHE=45°.