探析分类讨论法在初中数学解题教学中的实践

朱军平

【摘要】在我国初中阶段，数学学科作为一门复杂学科，具备严密逻辑性，同时，也是学好其他学科的重要基础.初中数学在教学过程中，要求立足于课本教学实际情况，制定符合学生特点的教学方法，能够通过激发学生兴趣，进一步提高学习成绩.当前在初中数学教学中，分类讨论思想不仅是学生学习难点，同时，也是考试重点，因此，作为数学教师需高度重视分类讨论思想，在课堂教学中的重要应用，同时在课后需布置分类讨论思想相关习题，能够使学生熟练掌握分类讨论思想的作用和应用.

【关键词】分类讨论法;初中数学;解题教学

1 分类讨论思想应用原则

分类讨论思想在运用时需要遵循互斥性和多层次性原则.比如初二某班级共有7名学生参与田径比赛球类比赛，其中4名学生参与球类比赛，5名学生参与田径比赛，表明在所罗列的7名学生中有同时参与两项比赛的学生，并且为两名，不能将7名简单进行田径比赛和球类比赛分类，否则会出现逻辑错误，在数学课题讲解过程中经常会遇到复杂问题，通常可采用二分法，结合对象层次进行逐层分类.

2 分类讨论思想具体应用

2.1 数值比较

要想使用正确分类讨论法解题，要求明确分类对象，具体包括对象、范围、性质等相关因素，同时确定对象之后，按照对象性质、属性完成分类，分类对象标准统一，不能出现重复和遗漏问题，需合理划分，分清主次，不能出现越级讨论的现象，这也是运用分类讨论思想解题的关键.

例1比如在有理数a与8a大小比较时，首先，需分析两数均是和有理数a相关的数字，a作为字母表示有理数，根据有理数分类，其具备不确定性，同时，在这一道题中还涉及有理数分类的概念.根据题目要求，当a大于等于a，此时a大于零时，a与B均为正数，由正数比较法则，绝对值大，那么该数值就大，因此a小于8a，当a=零时，此时a=8a=0，当a小于0时，此时a与8a均为负数，根据负数比较法，则绝对值大，该数值越小，因此a>8a.

例2 如果m-n=n-m并且m=4，n=3求（m+n）（m+n）的数值，对于该数学题需采用分类讨论法进行求解.首先，应当明确绝对值概念，涉及绝对值的问题，需进行分类讨论，只有通过分类讨论才能够得到完整且正确的结论，如果不进行分类讨论，会导致结果出现错误，对于该问题进行分析解答，由于m=4，n=3，因此m=±4，n=±3，又因为m-n=n-m，因此n-m≥0，n>=m，当n等于3时，m取值可能为-4.最终结果为1，如果a=-3时，m取值为-4，最终结果为49，所以（m+n）（m+n）数值为1或49.

2.2 方程求解

确定分类讨论对象之后，需要进行分类标准确定，通常标准是统一的，需合理进行分类，要求无互斥、无遗漏，无重复，做好相关准备工作之后，即开始进行分类讨论.

例3比如结合参数的取值范围分类，讨论求解含有参数的相关问题.比如关于X的方式方程进行求解，

x-ax-1-3x=1

已知该方程无解，求a的数值.类似这种问题需进行分类讨论.在求解该方程时，两边同时乘x（x-1），那么能够得到

（x-a）×x-3×（x-1）=x×（x-1），

经过整理，

（a+2）×x=3，当a+2=0时，

此时a=-2，

该方程无解，那么原有方程也无解，如果当x=1那么原方程无解，

此时（a+2）×1=3，a=1.

综合上述研究，如果原有方程无解，那么a的取值为1或-2.

例4比如在分式方程3x-3+axx2-9+=4x+3中，要想求解a的值，可需要借助分类讨论思想.

解

经过去分母之后能够获得下列公式

3（x+3）+ax=4（x-3）

（a-1）x=-21，

已知-21a-1=-3或者21a-1=3，或者a-1=0，因此a=8a=-6或1.

在这种变式中将无解变为有增根，如何进行求解？ a=8或a=-1.

此外，在一元二次方程中同样也可运用分类导学思想，比如在m2x2+（2m+1）x+1=0方程存在实数根，需要求解m的取值范围.对于这种情况下可将其分为两种情况：第一，如果m2=0，此时m=0，该方程为一元一次方程，那么x+1=0存在实数根x=-1;第二，如果m2≠0，此时该方程为一元二次方程，所求方程存在实数根，所以？（2m+1）2-4m2=4m+10那么m大于1/4，此时m2≠0，综合来看m应该大于-1/4.

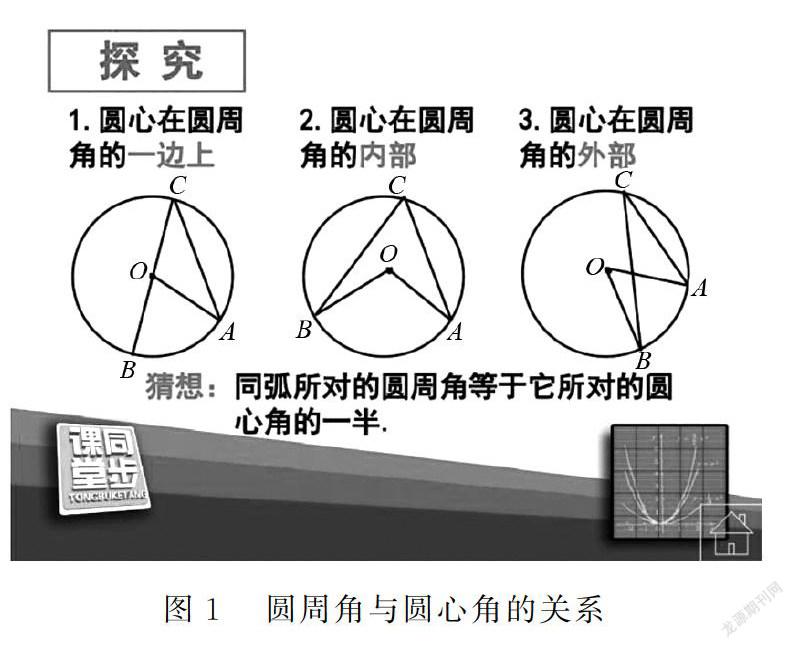
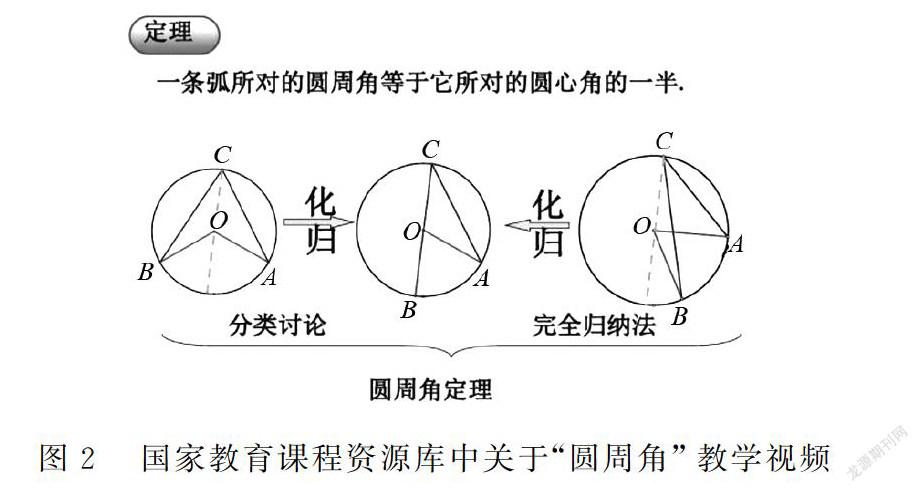
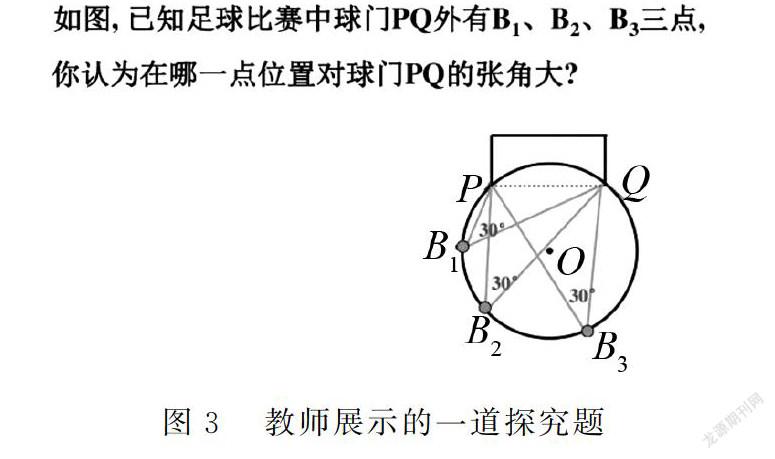
2.3 在圆和三角形中的运用

分类讨论思想也可用于圆和三角形等一些几何图形中.

例5 比如已知某函数y=- 33x+3 3在x，y軸交点分别为A、B两点.在x轴中寻找一个点P，使得？PAB为等腰三角形.对于这一类题由于在？PAB中P点的位置不确定，因此无法确定？PAB，且不清楚哪两条边为等腰三角形的腰.这种情况下对于？PAB来说存在三种情况，可将其分为：第一，PA=PB;第二，PA=AB;第三，PB等于AB，此时分别求解B的坐标为（0， 3），a点的坐标为（9，0）设置P点为（x，0），利用两点距离公式，针对上述三种情况罗列对应方程，可求出P点坐标为（-9，0），（9+6 3，0）（9-6 3，0）.在上述例题中舍去不满足条件的解集.

在解答这一问题中很容易出现漏解的问题，因此在解答时需考虑图形可能存在的位置，紧扣题目中已知条件分类，画出符合条件图形.

由于部分几何问题或者实际应用问题题目已知条件和结论不是唯一的，这种情况下也要对此进行分类讨论.

例6 已知在△ABC中，两边a=6，b=8，此时求解第三个边.

解

第一，当△ABC为直角三角形，此时c为斜边时c=10，如果c不是斜边，由于8>6，那么b为斜边，因此c= 82-62= 7.

第二，当△ABC为锐角三角形，此时由于a

①b2

②C2

③b

④c

由于①和②均屬于锐角三角形，③和④保证存在三角形，而③和④可通过①和②得出，

因此b2

第三，当△ABC为钝角三角形，此时由于a

那么C2>a2+b2ca2+c2b

此时10

2.4 点运动变化

由于点运动变化也会引起分类讨论，由于运动导致的点存在不同位置，需针对不同位置进行求解，否则会出现漏解.

例7 比如平面动点中分类讨论思想的运用，如下图所示，

已知在该正方形ABCD中，其边长为10厘米，P为动点，从A点出发，其运动速度为2厘米每秒，沿正方形边逆时针匀速运动.如图所示回到A点停止，当P点运动至t秒时，求取P，D两点之间的距离.对于该题根据已知条件可知，P点是从A点出发分别到达B、C、D，那么到达A点左右时间为10/2秒，20/2秒，30/2秒，40/2秒，也就是5秒、10秒、15秒、20秒，因此可将其分为以下几种情况：第一，t介于0～5之间，此时P位于线段AB中.那么PD=P1D= （2t）2+102=2 t2+25厘米.

第2，如果t介于5～10之间，那么P点位于线段BC上，此时PD=P2D.由此可回顾之前所学椭圆相关概念界定，视椭圆半长轴a可变，也就是说a为参数，这种情况下可令2c= （8-2）2+（3+5）2=10，在该椭圆中2a>20C，因此结论是成立的.意味着结论，可加强，将89/9替换成10，此时不等式仍然成立.

参考文献：

[1]李国巍. 分类讨论思想在初中数学教学中的应用方法分析[J]. 2021（2020-14）：13-14.

[2]包吉明.分类讨论思想在初中数学解题教学中的运用探究[J].好家长，2019， 000（003）：152-152.