初中物理解题中极限思维法的有效应用
时华夏
【摘要】在物理学发展历程中,极限思维法始终占据着重要地位,现在已经成为一种常用的解题方法.在初中物理解题教学中,教师可指导学生有效应用极限思维法,使其发散思维,转变固有的思维模式,能够触类旁通、举一反三,让他们学会运用极限思维法解答物理问题.笔者主要对初中物理解题教学中怎么应用极限思维法进行探讨,同时列举部分有效举措.
【关键词】初中物理;解题教学;极限思维
极限思维法即将复杂的物理过程进行分解,分解的小过程变化单一,因此,选择整个过程的两个端点和中间的极限对问题进行分析,在结果中包括物理过程讨论,更加直观、简单的解答问题.初中物理教师在解题教学中指引学生有效应用极限思维法,让他们迅速找到准确的解题思路以及方法,使其解题过程变得事半功倍.
1 利用极限思维法,找准问题入口
物理是学生在初中时期才接触到的一门新科目,他们在处理物理题目时,往往无法读懂题意,更是无法判定出各个数值在题干中所起到的作用,无法找到问题的入口.而且传统的解题方式極易限制学生的思维,解题过程显得程序化,难以找到快捷的解题方法,初中物理教师可指引他们利用极限思维法找准解题的切入点,使其在较短时间内就确定解题方法.
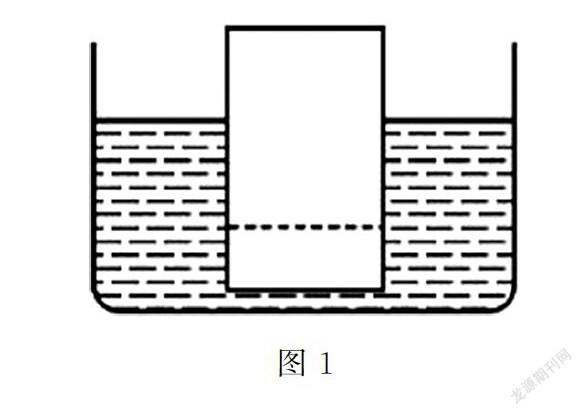
例1 在杯子中盛有半杯水,将一块木块放入其中,木块上半块浮出水面,沿着图1中的虚线位置将木块下部分截掉,那么剩余的木块位置将会发生什么变化?[1]
解析 如果使用传统的解题方式,学生将会考虑到木块的密度是均匀的,无论是否将下半部分截掉,都一定会浮在水面上,不过当木板的下半部分被截掉以后,体积将会变小,受到的浮力同样会变小,判断出木板的位置同之前相比会有所下降.运用极限思维法时,学生可反向思考,根据题目中的要求,将木块的下半部分截掉,木块依然处于水中漂浮状态,因为木块自身密度没有发生变化,导致木板仍然能够在水中漂浮,因此,木块下半部分也一定会浸泡在水中.在解题中,引导学生利用极限思维法,快速找到解题的切入点,以免出现计算数值的繁琐,有效节省解题时间.
2 运用极限思维法,活跃学生思维
物理作为一门典型的自然科学类科目,学习这类课程知识时,最担心的一个问题就是学生“钻牛角尖”,思维陷入到瓶颈之中,出现固定不变的情况,甚至很难发生转变,以至于他们无法顺利学习.在初中物理解题教学中,教师应该采取多种方式调动学生的解题兴趣,使其学会运用极限思维法来解题,让他们思维变得活跃起来,在解题中表现得更为高效[2].
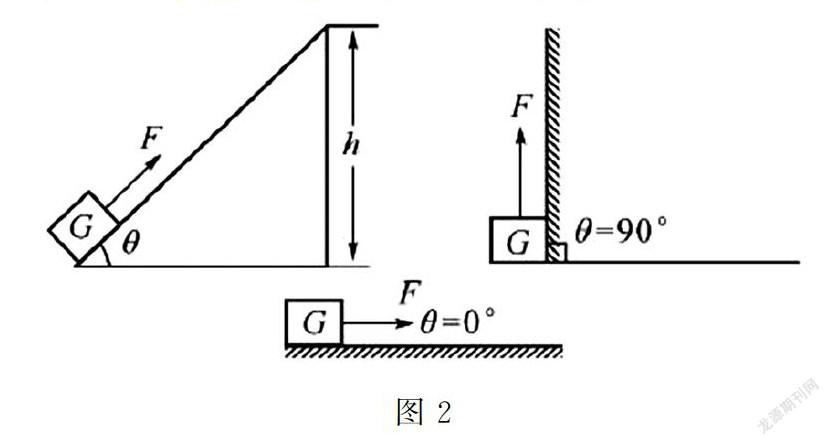
例2 如图2所示,在平行斜面上向上拉一个物体,斜面机械效率受到哪些因素影响?
解析当把一个物体往斜面上拉时,一定会出现摩擦力,因此,需要做有用功,机械效率高低和额外功存在很大的关系,额外功越高,机械效率就会越低.同时,额外功的大小还同摩擦力存在联系,大小和摩擦力基本相同,摩擦力的大小和物体压力相同,同时和斜面的粗糙度有着直接联系;物体压力大小和斜面倾斜度大小有着联系,倾斜面角度越大,物理压力则越小.结合极限思维法进行分析,倾斜面的倾斜角度和机械效率相关,斜面角度越大,则压力变小,当压力变小后,物体对斜面的摩擦力会减小,摩擦力越小,则其额外功就越小,额外功越小,则其机械效率就会越高.因此,机械效率高低和物体压力、斜面粗糙程度、倾斜度有着密切关系.
3 应用极限思维法,解决力学问题
力学整个物理知识体系的基础,在初中物理解题教学中,不少力学问题中都会存在角度或者长度的变化,这个时候通常可以采用极限思维法来分析试题,考虑角度或者长度变化中区间端点的特殊情况.初中物理教师可指导学生把题中的数值、物理量的方向推向某一个极端值的状态,降低力学问题难度,明确学生解题思路,使得解题思路更为简化[3].
例3 在某一角度可变化的斜面上放置一个由细绳牵引的物体,质量是G,角度变化的范围是0°—90°,在整个牵引过程中,保持物体处于静止状态,如果斜面的摩擦力足够大,当倾斜角从0°增大至90°的过程中,物体受到的支撑力有着什么样的变化?
解析不少学生认为,由于物体在斜面上处于静止状态,所以受到的支撑力有可能是不变的,教师可提醒他们分析题目中出现的变化量,即为斜面的角度,使其应用极限思维法,直接思考变化角度区间的两种极限情况,也就是0°与90°的情况.
当斜面角度是0°时,物体承受的支撑力大熊和物体的重力相同,当倾斜角是90°时,物体承受的支撑力为零.因此,在整个变化中,物体始终保持静止状态,因此,物体受到和支撑力相同且相反的平衡力,变化过程保持其连续性,则物体所授支持力的变化范围是0—G.
4 巧用极限思维法,解答运动问题
初中物理学习中,运动类题目是非常常见的题目,在问题解答中需要应用到极限思维法,在具体的使用中,应当引导学生对题目中的物理量进行梳理,并紧密结合实际生活,不能脱离基本事实与违背物理原理,使其根据具体解题需求确定好进行极限化处理的物理量,把运动学问题变得简单易处理,提升他们的解题效率[4].
例4 甲、乙两地之间有一条河流,其中甲位于上游,两地之间的距离是s,现在有一艘小船从甲处行驶至乙处,速度是v,达到乙处以后立即向甲处返回,已知往返一次的时间是t,那么下列选项中表述正确的是()
(A)t>2s/v(B)t=2s/v
(C)t<2s/v (D)上述情况均有可能.
解析 假如使用传统解法,需考虑到船速与水速的合成,并结合路程列出计算式求解,过程显得较为复杂,不适用于选择题,而使用极限思维法处理这一运动类问题,就显得没有这么繁琐.具体来说,本道题目中主要涉及到路程、水速与船速三个有关运动的物理量,学生采用极限思维法时,首先需考虑将哪一个物理量进行极限化处理,分析以后发现最恰当的是船速,当船逆流返回到甲处时,如果和水流的合成速度为零,那么船则无法返回,因此,返回的时间则是无限大的,即为本题的正确答案是选项(A).
5 借助极限思维法,解答电学问题
初中物理课堂中,部分电学问题较为复杂,属于难度相对较大的题目,要想更好地处理这类物理试题,需要加强课堂引导,利用电路图的优势,对问题进行分析,针对存在滑动变阻器等范围变动的问题,应更为灵活地使用极限思维法,使其准确找到处理问题的区间,找出不同物理量在不同区间的极值,完成电学问题的思考和解答[5].
例5 将一个滑动变阻器和定值电阻串联,构建成电路,其电压是220V,互动变阻器的阻值范围是0—100Ω,定值电阻为10Ω,在滑动变阻器的滑片移动中,电压表的读数范围是多少?
解析 在处理这道电学类的题目时,学生应找到本题中出现的变化量,即为滑动变阻器的阻值大小,因为是一個变化的区间,所以运用极限思维法解题时,可以把滑动变阻器的两个端点阻值大小当作计算依据,即为0Ω与100Ω.具体解答过程如下:运用极限思维法对滑动变阻器的阻值情况进行极限处理,当滑动变阻器接入电路的阻值是0Ω时,电路中电流最大,此时的定值电阻两端电压最大,即220V;当滑动变阻器的阻值是100Ω时,定值电阻两端电压值最小,即为20V,那么本题的正确结果就是定值电阻两端所测定的电压表读数范围在20V至220V之间.
6 采用极限思维法,解决压强问题
压强是一个表示压力作用效果的物理量,指的是物体所受压力的大小与受力面积之比,压强越大,压力的作用效果就越明显.
在初中物理课程教学中,压强也是一个比较重要的知识点,还是中考中的必考点之一,处理部分压强类的问题时,教师引导学生利用极限思维法,对物体压强做出分析,使其找准解题的突破口,帮助他们形成清晰的思路[6].
例6 在水平面上,放置有两个不同高度的实心金属圆柱体,两个圆柱对地面压强相同,从水平方向就能够两个实心金属圆柱体截掉相同高度,两个金属圆柱体剩余部分对水平面的压强有着怎样的关系?
解析 在此题解答中,题目中并没有明确给出实心金属圆柱体的高度,同时,对圆柱体截取的高度也没有提出,题目中的已知条件比较少,内容较为抽象,解答的难度比较大.
在解题中,如果让学生采取传统解题思路,需要利用压强公式计算圆柱体密度的关系,截取高度相同,那么,密度较大的金属圆柱体剩余部分产生的压强较小,此种解题方式计算繁琐,分析过程也比较复杂,很容易出现解题错误.
作为教师,引导学生利用极限思维法解题,将截取金属圆柱体高度最大化,当截取的金属圆柱体高度和较低圆柱体高度相同,那么较低实心圆柱体则就被完全截取,对水平面的压强是零,另一个实心圆柱体依然有剩余,对地面压强则不可能是零,通过这样可以轻松解答题目,即可以得出较好实心圆柱体被截取后对水平面的压强较大.
处理初中物理中的压强类试题时,通常会涉及到高度变化问题,教师就需引领学生采用极限思维发,对最大长度展开考虑,并把握好长度区间的变化,把变化的物理量推向某一个极端,以此更好的判断出物理量的值,提升他们的解题水平.
7 总结
在初中物理解题教学活动中,由于学生在初中阶段才开始接触物理学科,解题过程更为繁琐,既要分析、又要计算,容易遇到思维障碍,很多时候甚至一头雾水,不知道从何处下手,教师应多指导他们运用极限思维法处理题目,使其思维得以充分发散开来,学会进行逆向思考,继而不断提升自身的物理解题能力,同时掌握更多解答物理问题的技巧与方法.
参考文献:
[1]凌习华.初中物理解题中的极限思维运用[J].数理化解题研究,2021(29):83-84.
[2]胡庆霞.极限思维在初中物理解题中的融合[J].数理化解题研究,2020(08):78-79.
[3]张晓芳.极限思维法在初中物理解题中的妙用[J].试题与研究,2019(30):144.
[4]李花.探究极限思维在初中物理解题中的应用[J].数理化解题研究,2019(08):45-46.
[5]杜云伦.极限思维在初中物理解题中的应用[J].数理化解题研究,2019(20):58-59.
[6]徐红伟.探讨极限思维在初中物理解题中的应用[J].数理化解题研究,2019(17):69-70.

