当量实心板计算管板应力的方法介绍

牟力波

(哈电发电设备国家工程研究中心 黑龙江 哈尔滨 150028)

0 概 述

随着国内制造能力不断提升，管壳式换热器在工业设备中的使用数量逐年提升，且呈现高参数、大型化的发展趋势。管板是管壳式换热器的主要受压部件之一，管板的合理设计，对合理选择和节省材料，降低加工制造工艺的难度具有重要意义。由于管板结构的复杂性，影响管板强度的因素较多很多，所以现行各国规范的管板厚度计算公式，都是对实际管板作一定的简化假定而得到的近似公式，由于所采用的简化假定各不相同，与管板实际受力状况必然有不同程度的差别，造成在同样条件下用采用现行的各国规范计算公式得到的计算厚度也有差别，同时对于近似公式的计算，往往有其限制条件或适用范围，对于超标准设计管壳式换热器管板时，往往采用应力分析法。

应力分析法计算管板时，常采用三维实体模型，模型包含管板、换热管、法兰、螺栓螺母、垫片等，模型网格节点多达几百万个，同时，当垫片密封处设置了接触，计算过程往往需要2～3天，大部分时间花费在求解节点的刚度矩阵和载荷矩阵上，计算分析效率极低。

1 管板分析设计的基本考虑

从管板分析数学模型上考虑，假设管板作为承受规则排列的管孔削弱、同时又被管子加强的等效弹性基础上的均质等效圆平板来计算，结合管板实际结构及工况，还应考虑以下因素：

a.管板周边部分较窄的不布管区按其面积简化为圆环形实心板；

b.管板边缘可以有各种不同型式的连接结构，各种型式可能包含有壳程圆筒、管箱圆筒、法兰、螺栓、垫片等多种元件，并按各元件对于管板边缘的实际弹性约束条件进行考虑；

c.考虑法兰力矩对于管板的作用；

d.考虑换热管与壳程圆筒间的热膨胀差所引起的温差应力，还应考虑管板上各点温度差所引起的温度应力。

e.计算换热管的多孔板折算为等效实心板的各种等效弹性常数与强度参数。

基于上述几点，综合考虑管板的结构和受力特点，可以将管板简化为一个载荷对称、结构对称、材料属性对称的轴对称问题，据此管板可以简化为当量实心板分析计算。

2 管板当量实心板应力计算

管束主要由管板和换热管组成，管板为大平板上开同规格管孔，既有管孔的消弱也有换热管的加强，如果不考虑换热管的加强，可以将管板简化为多孔平板，在受到同等载荷下，多孔板中的应力大于实心板，如果假设多孔板与实心板中的应力相等，反求实心板的本构关系，得到的实常数，即为需要修正的常数值。

基于上述概念，根据参考文献[4]，采用多孔板的有效弹性模量(E*)和有效泊松比(μ*)代替板的弹性模量(E)和泊松比(μ)，就可用普通板的常规公式来确定当量实心板的名义应力。E*和μ*是孔带系数(η)的函数，对于0.05≤η≤1.0范围内的E*在图1(孔带系数与有效弹性常数关系图)中μ*对η和E*/E对η的形式给出，计算或分析是只要用孔带系数(η)将板的弹性模量(E)和泊松比(μ)折算成用多孔板的有效弹性模量(E*)和有效泊松比(μ*)，就可以计算出当量实心板名义应力，再按图2(计算双轴比与应力修正系数(K)的关系图)查的修正系数(K),乘以实心板名义应力，即可确定多孔板应力强度的实际值。计算双轴比为管板径(周)向与周(径)向应力比值(β)。

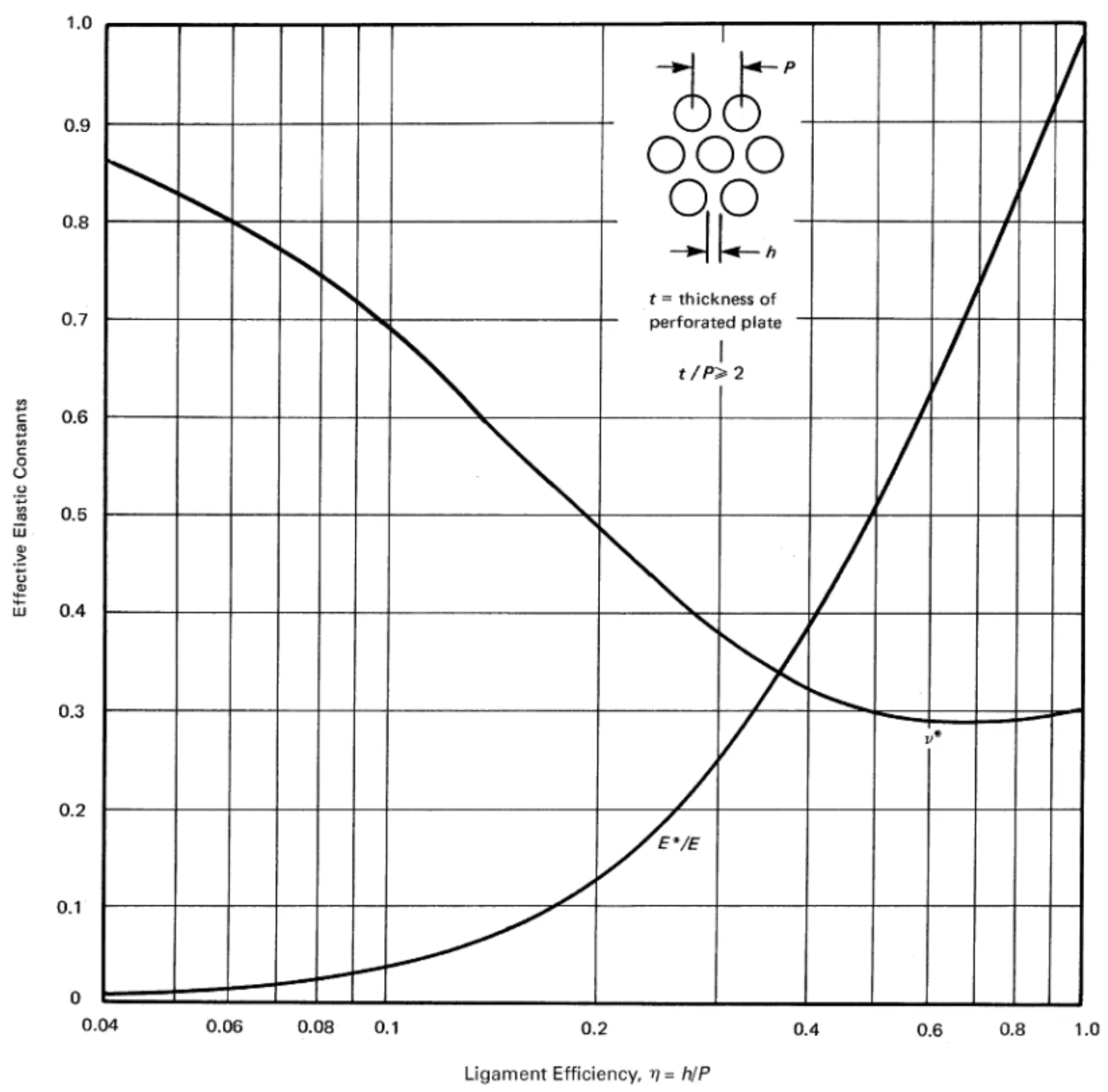
图1 孔带系数与有效弹性常数关系图[4]

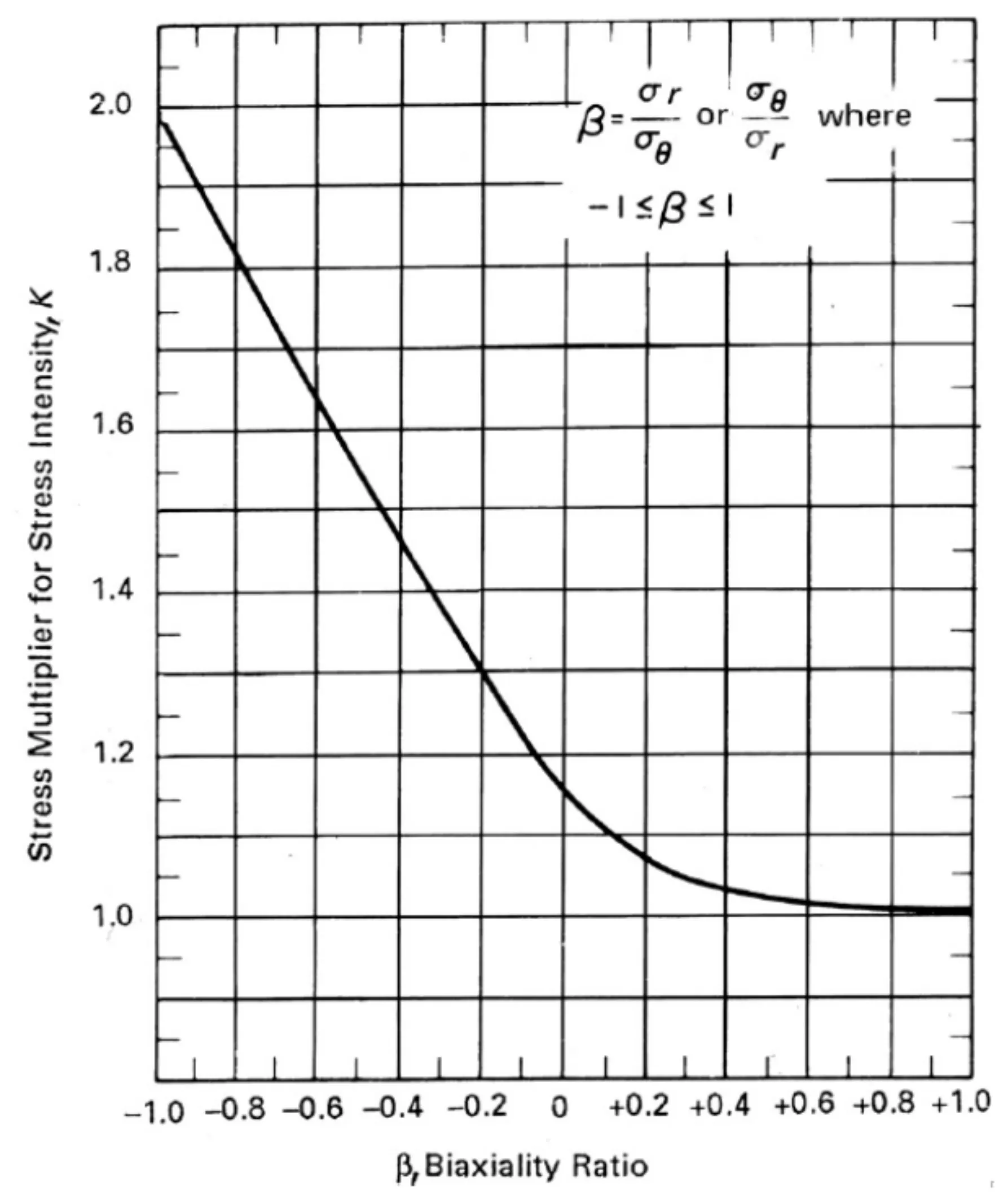
图2 计算双轴比与应力修正系数(K)的关系图[4]

3 公式法计算管板应力

根据参考文献[3]，管板当量圆平板后，受力以圆形薄板在横向均布压力作用下为数学模型，应力不仅和位置有关，也与周边支承方式有关，以管板两侧简支，正三角布管为例介绍多孔管板应力计算方法，布管图见图3.根据管板两侧受均布压力载荷，管板的数学模型计算见图4.

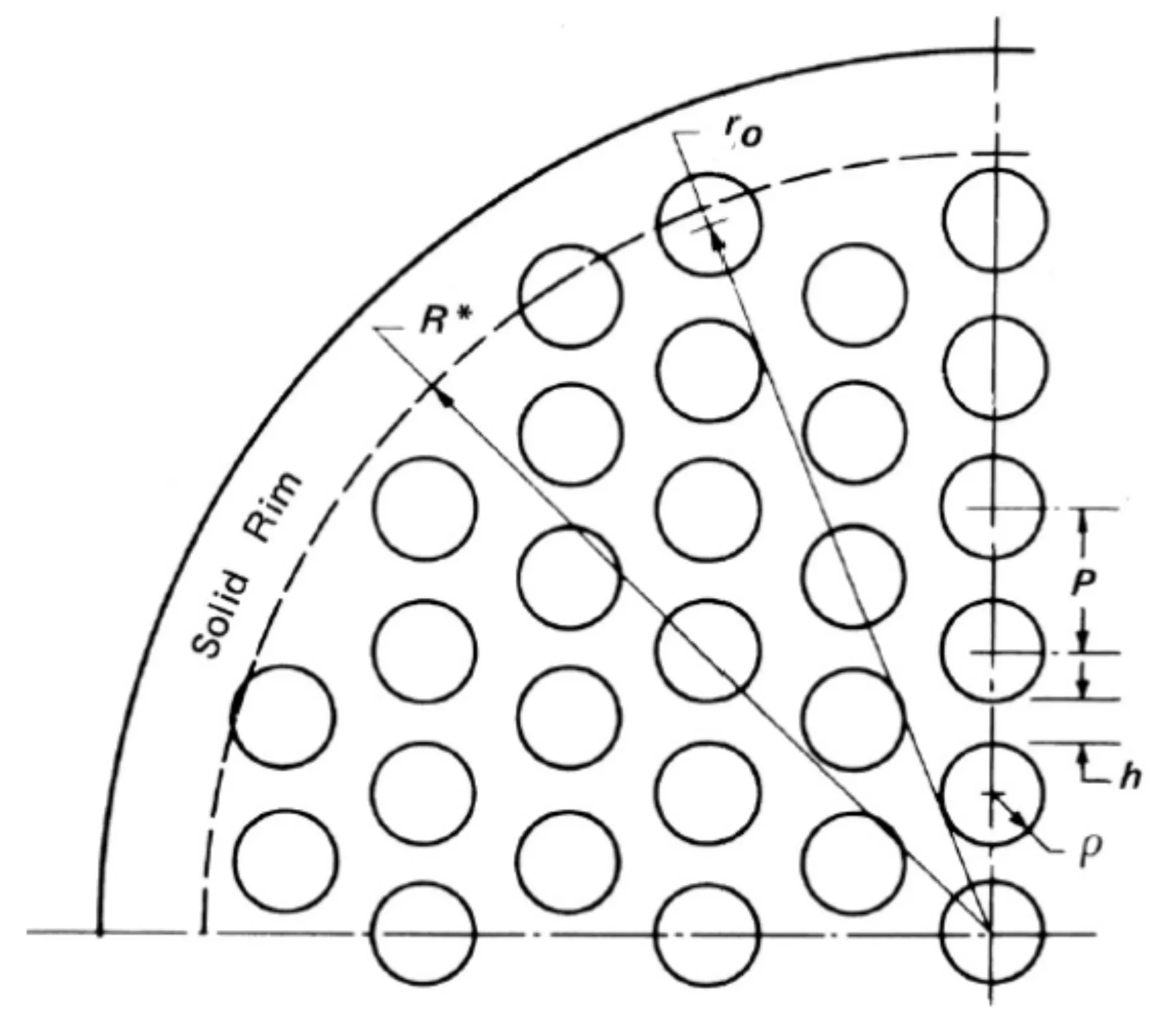
图3 管板布管图

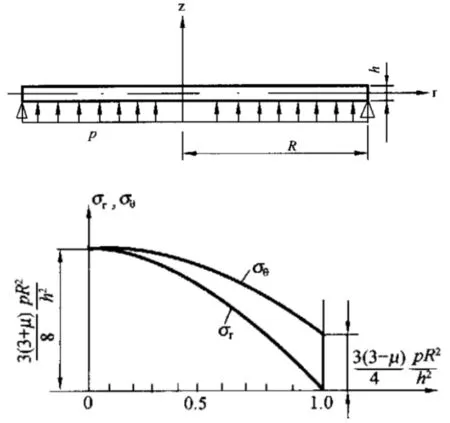
图4 当量管板计算(周边简支)

根据参考文献[1]:

径向弯曲应力：

(1)

周向弯曲应力：

(2)

在平板中心处：r=0，可得：径向弯曲和周向弯曲相等且有最大值

(3)

其中；R:为圆板外半径;μ:泊松比；P:横向均布压力；δ::圆板厚度。

管板当量实心板后的受力图见图5当量管板受力图，化简公式(1)和(2)得管板表面上任意r处的应力为：注意公式(6)的弹性模量E采用当量前的实际值。

径向弯曲应力：

(4)

周向弯曲应力：

(5)

中面边缘挠度：

(6)

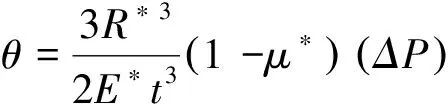
(7)

其中：

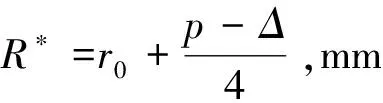
μ*：当量后泊松比,无量纲，根据孔带系数η查图1得出

E*：当量后弹性模量,MPa，根据孔带系数η查图1得到E*/E比值，计算出E*

r：从管板中心沿径向的任意取值,mm

ΔP:管壳侧压力差，MPa

t: 管板厚度，与图4中h相等,mm

r0：从管板中心到最外孔中心的径向距离，见图3,mm

p:管心距，见图3，mm

h:孔带宽度,h=p-?，见图3，mm

Ø：换热管直径等于2ρ，见图3，mm

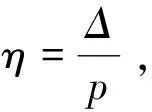
K:根据计算双轴比，按图2查系数乘数，无量纲

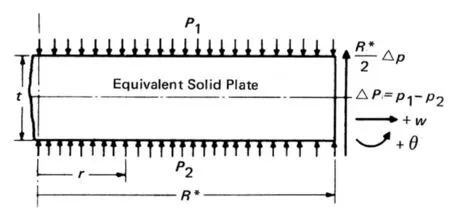
图5 当量管板受力图

4 应力分析法计算管板应力

根据参考文献[2，5]，采用应力分析法计算管板应力，根据多孔板当量实心板理论，简化换热管实体，采用正交各项同性定义材料属性，用孔带系数折算布管区弹性模量和泊松比，折算方法采用图1。模型其余部分按真实结构创建，通过示例说明其方法。

4.1 有限元几何模型

有限元几何模型见图6。

图6 有限元几何模型

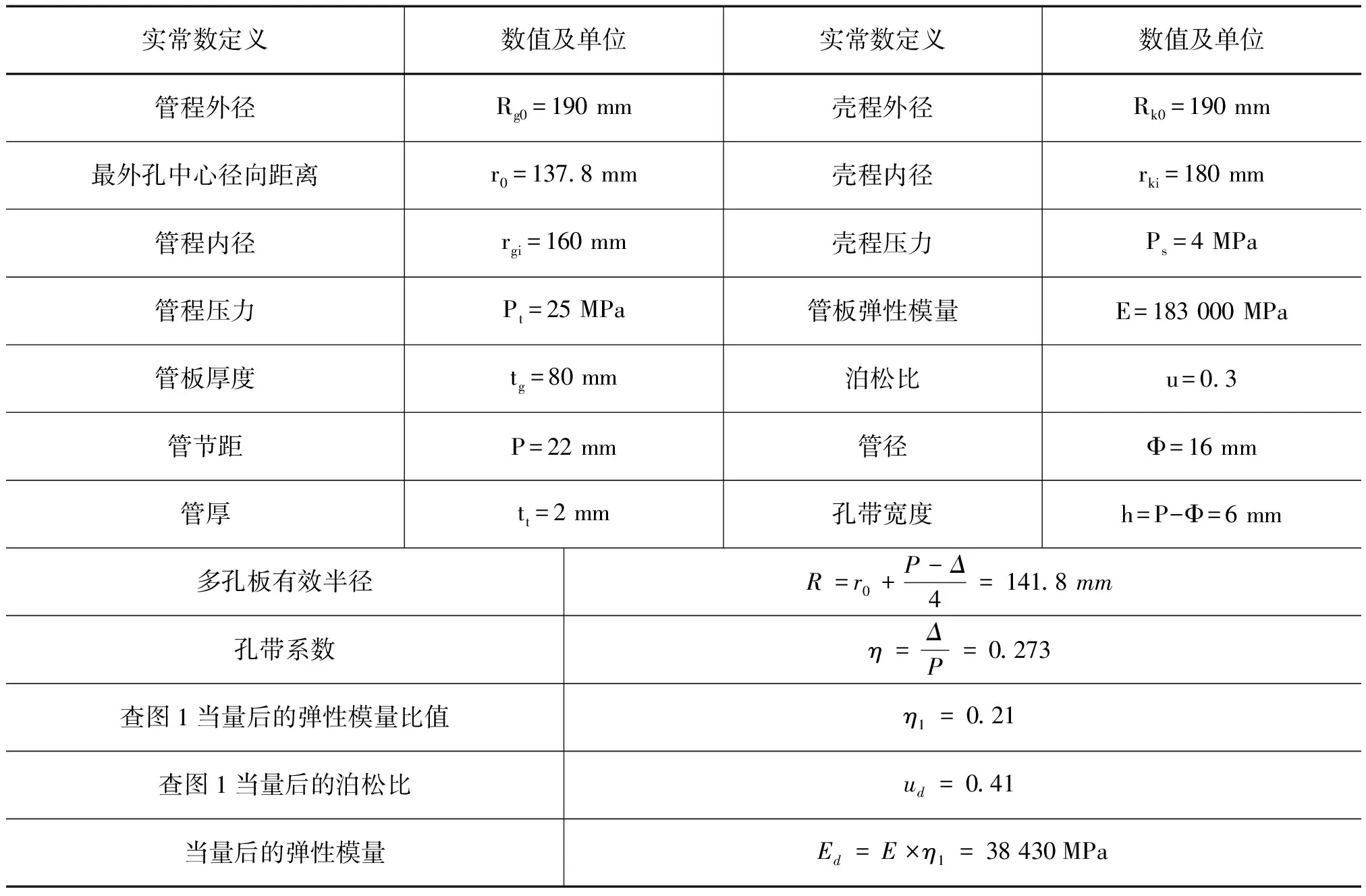
实常数定义数值及单位实常数定义数值及单位管程外径Rg0=190 mm壳程外径Rk0=190 mm最外孔中心径向距离r0=137.8 mm壳程内径rki=180 mm管程内径rgi=160 mm壳程压力Ps=4 MPa管程压力Pt=25 MPa管板弹性模量E=183 000 MPa管板厚度tg=80 mm泊松比u=0.3管节距P=22 mm管径Φ=16 mm管厚tt=2 mm孔带宽度h=P-Φ=6 mm多孔板有效半径R=r0+P-Δ4=141.8 mm孔带系数η=ΔP=0.273查图1当量后的弹性模量比值η1=0.21查图1当量后的泊松比ud=0.41当量后的弹性模量Ed=E×η1=38 430 MPa

4.2 模型实常数计算

4.3 有限元模型

有限元模型见图7。

图7 有限元模型

4.4 有限元边界条件及结果路径设置

有限元边界条件及结果路径设置，见图8和图9。

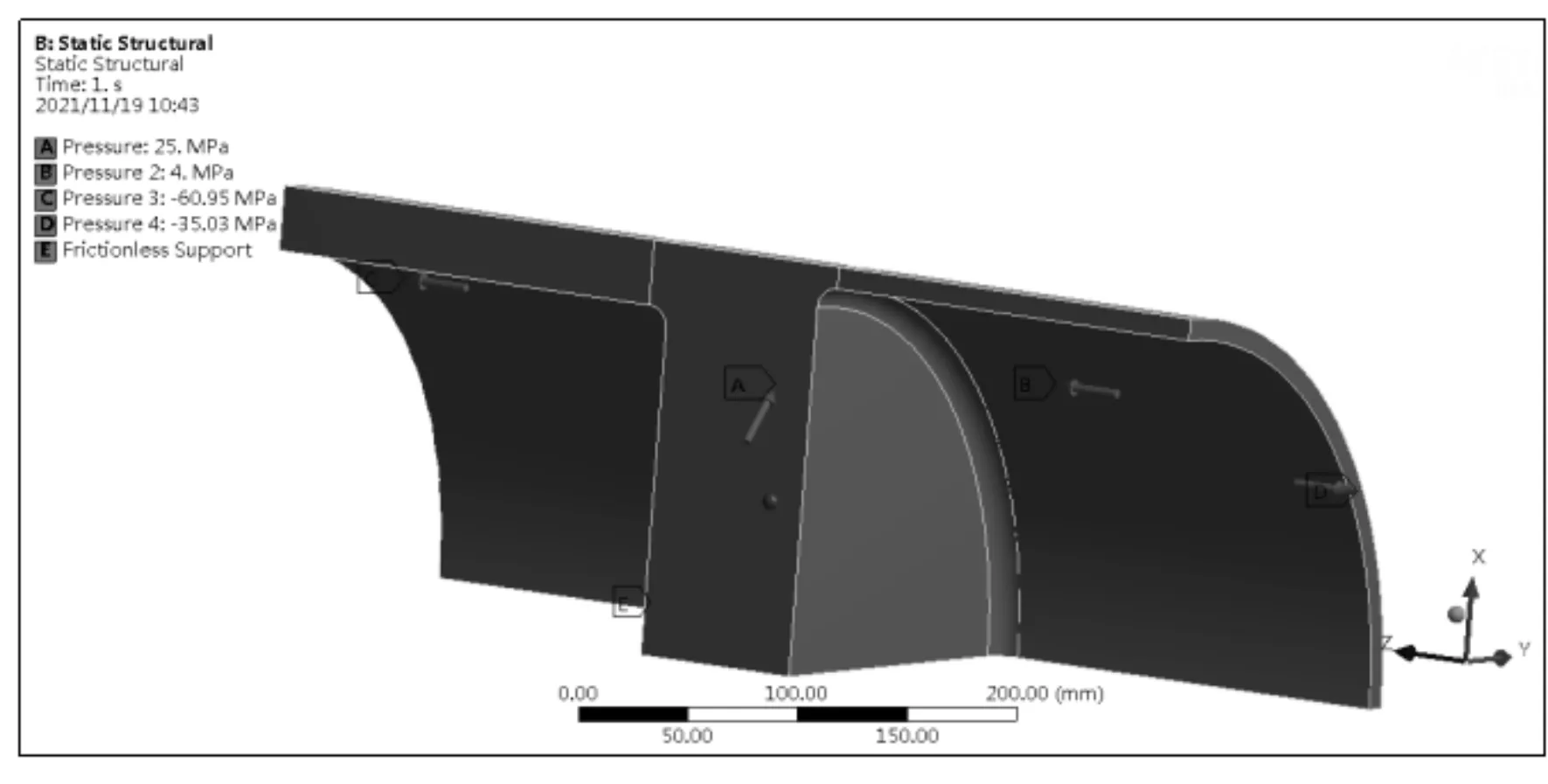
图8 边界、结果与路径设置图

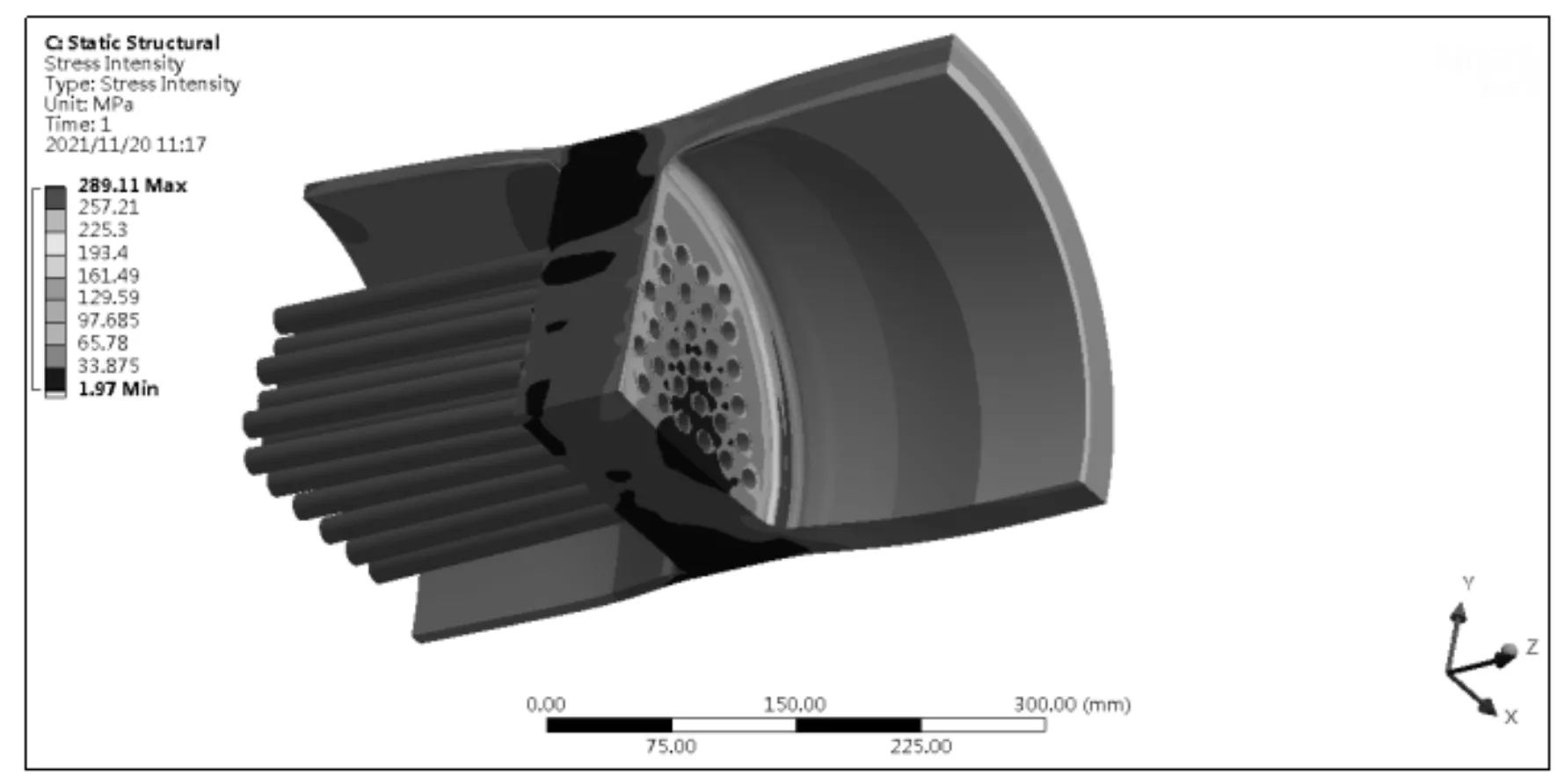
图9 未简化带换热管分析结果

5 管板应力限值

不管采用公式法计算还是采用应力分析法计算，对于薄膜应力(总体和局部)的限值按5.1确定，对于薄膜+弯曲应力限制按5.2计算。

5.1 薄膜应力限制

对于沿最小孔带宽度和沿板厚上取应力的平均值的应力强度，即薄膜应力，取下列S1和S2的较大值,求解示例见表1和表2。

式中其它符号意义参看第3节定义；

σr：沿当量实心板厚度取平均应力，MPa

5.2 薄膜+弯曲应力限制

沿最小孔带宽度取平均应力值(而非沿板厚的平均值)，按薄膜+弯曲应力限值。求解示例见表1和表2。

其中;K:按图2双轴比查取

σave：取④式和⑤式的最大绝对值。

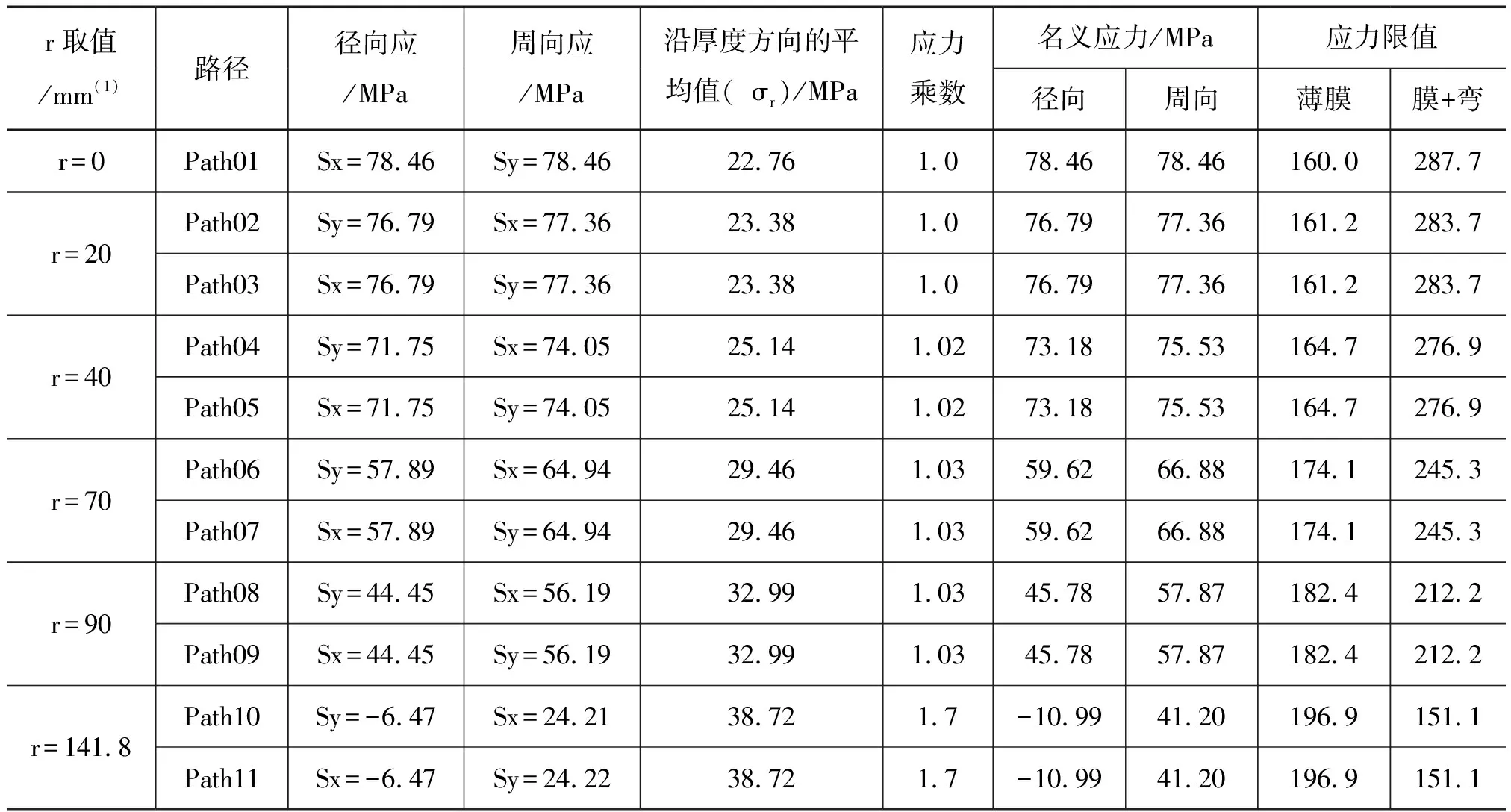
表1 应力分析法求解结果表

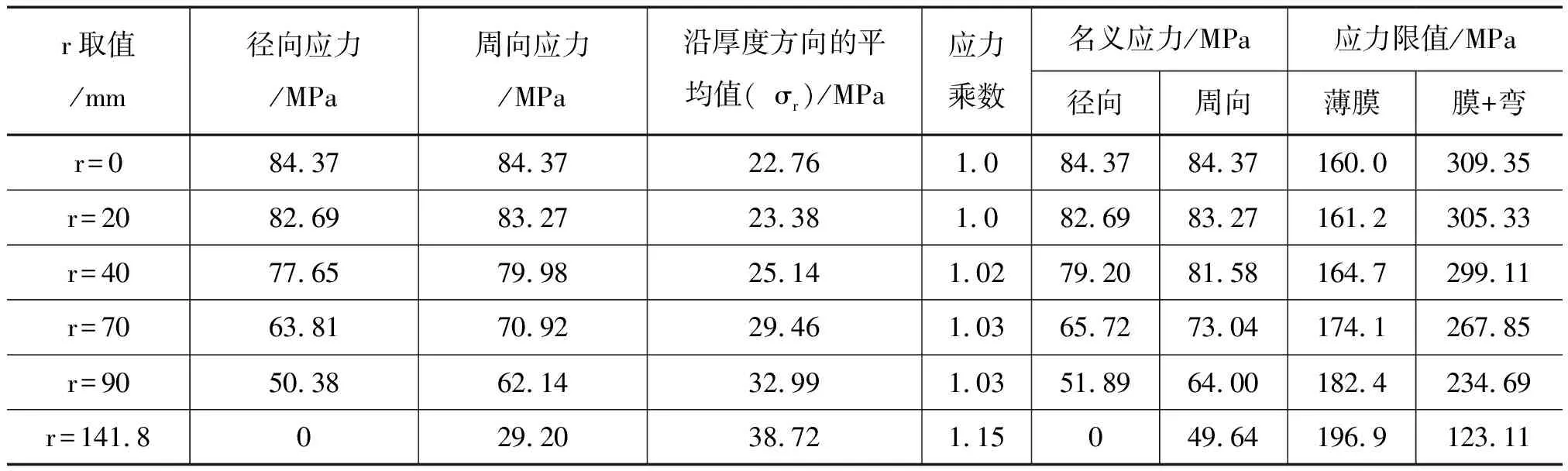
表2 公式法求解结果表

6 总 结

采用当量实心板计算多孔板中的应力，可以大大简化模型，提高运算效率。本文介绍了两种方法供读者使用，经对比两种方法，可得出以下结论。

1)当量实心板公式法计算比当量实心板应力分析法计算值保守，原因是公式法计算中考虑较为保守的计算策略，忽略对管板有益的条件；

2)两种方法计算结果一致，管板中心应力大于边缘应力，且中心应力径向和周向相等，任意半径处的周向应力大于径向应力，这两种应力随半径的增大而减小，符合管板理论分析；

3)对于管板计算分析时，优先选用当量实心板公式法计算，计算评定不合格时，采用当量实心板应力分析计算，若评定结果再不合格时，采用三维实体带换热管模型计算，如图9所示；

4)管板采用当量实心板计算，即为孔带减弱系数当量弹性模量和泊松比，是否可以采用孔带减弱系数进一步当量正交各项异性材料属性分析计算，此时模型可完全采用二维轴对称模型分析计算，届时可大大简化模型，提高运算效率。