例析高中物理综合类大题的解题策略

四川绵阳实验高级中学（621000） 朱忠胜

一、高中物理综合类大题的种类

综合类大题可从“综合”和“大”两个方面理解。“大”很好理解，一般从题干的“体量”就能直观看出它的“大”。综合类大题往往占据压轴题的“宝座”，是一套试卷中名副其实的“老大”，但让考生畏惧它的往往是“综合”这个关键词［1］。综观各类考试，很容易发现，综合类大题并不只是简单地考查一个知识点，而是综合考查多个知识点，甚至是跨学科综合考查，尤其容易与数学知识综合考查。总体来说，它可分为以下四大类：

1.力学综合类。这类题看似只有力学一个大知识板块，但是涉及的内容却是方方面面的，尤其是多过程问题、多体问题、多情况讨论问题。

2.复合场类。这类题一般以某类粒子为研究对象，研究其进入电、磁复合场的复杂问题，其中复合场又分为临界复合场和组合复合场，复合场还分无边界复合场和限制边界的局部复合场，粒子的运动也分为依次进入不同场运动和直接进入复合场运动，等等。这类情况最常见的是多过程问题和多情况讨论问题。

3.电磁感应类。这类题多在电场和磁场的大小、方向变化上做文章，使问题变得复杂，常结合相关图像对学生的解题能力进行考查。

4.力电磁综合类。这类题综合以上三个类型，可以说是对高中物理知识的“大乱炖”，它往往表现为研究过程复杂、物理情境多变、解题思路隐蔽，需要学生对每一板块知识都有清晰的认知，还要能够灵活运用［2］。

总结总是笼统的，接下来我们先通过3 道例题来看看综合类大题的真面目。

二、例题分析

［例1］在一次学校运动会上，某体育老师模拟冰壶运动设计了一个简化版的比赛项目——推球比赛。比赛项目的规则是：如图1 所示，比赛选手在A点处用恒力F将静止的球推出，一段时间后撤去力F，让球沿着AC方向自由运动。若球最终停止在BC区域内，则得分；若球未停在BC区域内，则不得分。如图1中标记，已知L1=5 m，L2=1 m，比赛用球的质量m=0.5 kg。若推球的力为恒定不变的水平力，当球受到推力作用时其加速度的大小a1=36 m/s2，没有推力作用时其加速度的大小a2=4 m/s2，重力加速度g取10 m/s2，整个运动过程中球可视为质点。如果选手想要得分，则：

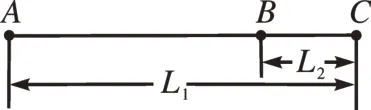
图1

（1）手作用在球上的最长时间为多少？

（2）手作用在球上的最短距离为多少？

分析：本题属于最基本的力学综合类题，涉及匀变速运动知识和几何知识，解题的关键是找到临界点，进而准确分析研究对象的运动过程，然后运用运动学公式结合几何关系列式求解。题中的关键点有：①球从A点开始运动，先受恒力作用，做匀加速直线运动；②手离开球后，球在摩擦力作用下做匀减速直线运动；③手作用在球上的时间越长，球运动的距离越远，若想得分，球最远的运动距离不能超过C点；④与③同理，若想得分，手作用在球上的最短距离，也必须要到B点。有了以上的认知，这道题就不难解决了。

解：（1）若想比赛得分，当球停在C点时，手作用在球上的时间最长。设手作用在球上的最长时间为t1，在t1时刻球的速度为v，由牛顿第二定律可得：

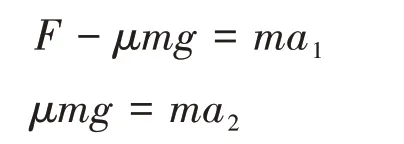
球匀加速直线运动过程中的位移为：

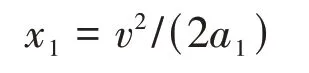
球匀减速直线运动过程中的位移为：

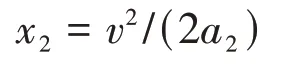
由几何知识可得：

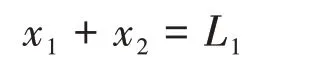
又知v=a1t1

（2）若想比赛得分，球至少要运动到B点，此时手作用在球上的距离最短，设该距离为d，手离开球时球的速度为v′，则有：

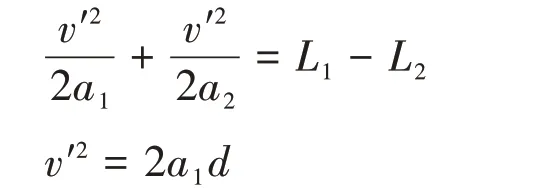
联立以上两式并代入题给数据可得d=0.4 m。

即若想比赛得分，手作用在球上的最短距离为0.4 m。

［例2］如图2 所示，在水平轨道的左端B点平滑连接着一个竖直放置的光滑半圆形轨道，O点是半圆形轨道的圆心，D点是半圆形轨道的最高点，C点是最左侧点，半圆形轨道的半径R为0.2 m。在水平轨道的A点静止放置一个质量m=3.0 kg、带电荷量q=+5.0×10-3C 的小物块。已知小物块与水平轨道间的动摩擦因数μ=0.2，点A、B间的距离L=1.0 m，重力加速度g取10 m/s2。

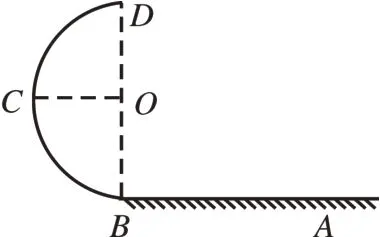
图2

（1）若加一个方向水平向左、场强大小E=2.0×103N/C 的匀强电场，则小物块达到最大速度时处在哪个位置？

（2）按照（1）中的情况，小物块会在水平轨道上运动的总路程为多长？

分析：本题属于力电综合类题，涉及力学问题中的多过程（直线运动、圆周运动和往复运动）分析，功能关系分析，还综合了电学的电场力做功、数学的极值求解，等等。解第（1）小题时，先要分析出功能关系，根据动能定理列出关系式，判断小物块的运动情况，尤其是判断出它是否会脱离半圆形轨道，然后通过数学知识求出极值。为了计算简便，还可以用“合场”思维求解，将重力场和电场进行等效替代。

解：（1）设小物块运动到半圆形轨道最左侧的C点处时，速度为vC，利用动能定理可得：

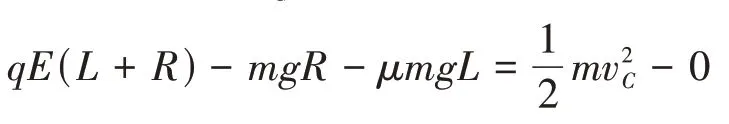
代入数据可得vC=0。

由此可知，小物块并没有脱离半圆形轨道，一直在系统所给的轨道上运动。

为了方便研究，可设电场力和重力的合力方向与竖直方向的夹角为θ。

如图3 所示，过O点作半径OM，OM与OB的夹角为θ，则可知M点就是合场中小物块做圆周运动时的最低点，也是小物块达到最大速度的点。由几何知识可知：

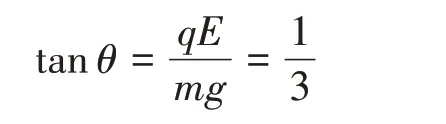
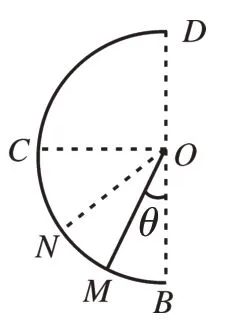
图3

（2）根据（1）中的结果分析，物块在以M点为中心的两侧往复运动，如图3所示，N点和B点是往复运动的左右端点，根据几何知识可知ON、OB与OM的夹角均为θ。

设小物块在水平轨道上运动的总路程为x，同样由动能定理可得：

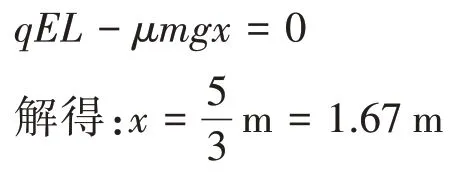
［例3］如图4 所示，在平面直角坐标系xOy的第一象限和第四象限内存在电场强度为E的电场Ⅰ和Ⅱ，电场方向如图4 所示，其区域分别为：电场Ⅰ在双曲线（在0 ≤x ≤L，0 ≤y ≤L区域）的一段与x轴、y轴围成的区域内；电场Ⅱ在直线x=-L、x=-2L、y=0、y=L所围的区域内。现有一个重力不计、带电荷量为-e的微粒。

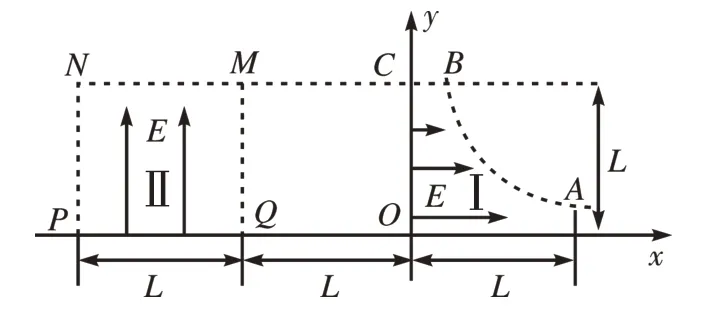
图4

（1）如将微粒由B点静止释放，求该微粒从电场Ⅱ中飞出时点的坐标。

（2）如将微粒从曲线AB上任一点静止释放，求微粒飞出电场Ⅱ时的最小动能。

分析：该题是一道组合电场题，带电粒子在不相邻的两个有界电场中运动，涉及数学的双曲线方程、极值计算，物理的加速直线运动、匀速直线运动、类平抛运动、动能定理等知识点，尤其考查学生的数学知识储备。

解：（1）由题意知B点在双曲线上，其纵坐标yB=L，可得其横坐标设微粒从B点运动到C点时的速度为v1，由动能定理得：

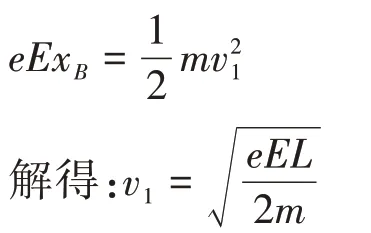
微粒从C点到M点做匀速直线运动，故可知微粒以速度v1从M点水平向左进入电场Ⅱ，然后做类平抛运动，设其在电场Ⅱ中的运动时间为t1，由平抛运动公式可得：

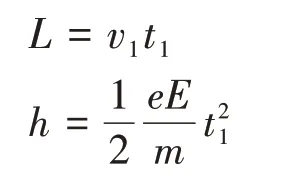
解得h=L，即微粒从电场Ⅱ中飞出时点的坐标为（-2L，0），也即飞出点为P点。

（2）设释放微粒的坐标为（x，y），微粒进入电场Ⅱ时的速度为v2，在电场Ⅱ中做类平抛运动的时间为t2，可得：

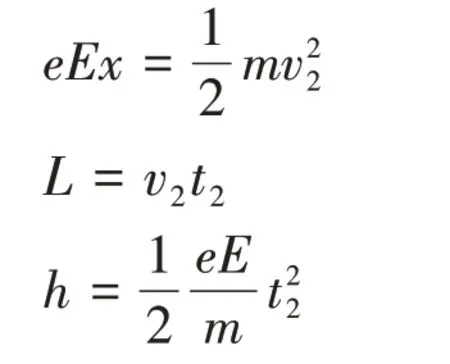
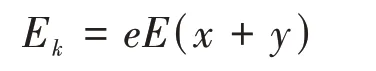
三、解题策略总结

通过上面例题的解析，不难发现，虽然综合类大题的物理情境复杂，涉及知识面较广，但是只要准确找到解题的关键点，用好相关规律公式，解决问题就容易了，甚至还有点“题大解小”的感觉。就如例2，如果不能巧妙利用“合场”思维找最大速度，将问题化繁为简，那么分析起来就会比较困难。

下面具体总结解决综合类大题的策略。

1.认真审题，深挖隐含信息。在考试中，尤其是高考这类重要考试中，综合类大题的设计者肯定会千方百计地设计陷阱，且常将有用信息巧妙换装或隐藏，因此解题时必须认真审题，深挖题中的隐含信息。题中涉及的物理现象、物理过程和所给图表都可能隐含着有用信息，需要对其做出准确判断。而要做到这一点，则需透彻理解物理知识。

2.准确选取研究对象，正确确立相互关系。尤其是面对多体问题时，选取正确的研究对象，是保证解题事半功倍的关键［3］。选取并分析研究对象时，常用的方法有隔离法和整体法，当然，有时需要将两种方法综合应用。选取研究对象后，就可以进行受力分析以及运动状态和运动过程分析，明确功和能关系，最终确定使用什么定理、定律列式求解。

3.认真分析制约条件，仔细思考多种可能情况。解决综合类大题时，要注意分析多种情况。尤其是遇到有制约条件（如复合场有边界、涉及竖直圆周运动等）的题目时，必须仔细推敲，逐类讨论，谨防漏解，以免造成“题会做却没能拿到满分”的遗憾。

4.认真计算，避免出现计算错误。综合类大题往往计算较多，还可能涉及三角函数等各种带小数的麻烦运算，个别题目对结果的精确值也会有要求，因此必须认真计算，按照题目要求给出结果。

总之，综合类大题看似困难，其实只要采取正确的战略战术，就能成功解题，取得高分。