氧煤燃烧熔分炉熔池内射流行为规律的物理模拟

申耀宗,张巧荣,赵 凯,甄常亮,齐渊洪

(1.华北理工大学 冶金与能源学院,河北 唐山 063210;2.钢铁研究总院先进钢铁流程及材料国家重点实验室,北京 100081)

现有高炉炼铁工艺面临碳排放大、环境负荷大等严重问题,制约了钢铁行业的绿色可持续发展[1-3]。非高炉炼铁工艺的开发是减少高炉炼铁碳排放的有效途径之一,其中熔融还原炼铁是当下研究的热点[4-6],以现有二步法熔融还原为代表的COREX 和FINEX 炼铁工艺已实现工业化生产,但仍存在铁水成本过高、无法完全摆脱对焦炭依赖等问题[7-9]。因此,综合分析各熔融还原熔炼技术,结合Romelt 熔融还原炼铁及有色冶金烟化炉,以煤基回转窑为预还原基础,提出了回转窑预还原-氧煤燃烧熔分炼铁新工艺[10]。氧煤燃烧熔分炉作为该工艺的核心反应器,冶炼过程属于高温封闭式冶炼,无法对熔池区域进行可视化研究,而对非稳态流体流场中相关特性的认知又是优化反应器结构、掌握流体运动机理的前提。

目前,有关高温密闭反应器的研究中,物理模拟[11-12]方法被广泛使用,其中BRIMACOMBE 和CASTILLEJOSE[13-14]等均是基于物理模拟的基础上研究反应器内的气液变化,而针对熔池内的射流流场情况,吴晅等[15]通过建立相关模型,对反应器中3 种不同的喷吹方式进行研究,表明气泡聚并行为的发生会对周围射流流场产生交互作用。Peng Yan等[16]以数值模拟为基础,发现了气泡所受作用力的变化会影响气泡之间的聚并概率,由此可知,气泡运动是反应器内射流流场变化的基础,而射流行为的规律又是单个气泡运动的整体表现。吕明等[17]通过结合理论计算和模拟分析,发现在圆形反应熔池内,随着顶吹枪位的提高,射流对熔池的冲击面积会伴随增加。LI Ming-ming 等[18]通过模拟结果预测了反应器中喷溅和射流冲击形状。综上可知,关于熔池内射流行为的研究大多集中在以圆形炉型反应器为基础的工艺中,对矩形熔池的研究还缺乏统一认知,而针对新型无焦炼铁反应器所采用的矩形侧吹浸没式熔池熔炼,熔池中射流行为的变化会直接影响熔池内熔炼及搅拌情况,稳定的射流行为会促进搅拌,提高熔池熔炼效果;紊乱的射流行为又会冲击炉衬,对耐火材料造成严重冲刷。

本研究通过水模拟实验,基于相似原理,搭建了5∶1的反应器模型,辅以高速摄像系统实时拍摄,对氧煤燃烧熔分炉熔池区域的射流行为规律进行研究。并以射流形态中单个气泡受力为基础,建立射流气泡上升运动模型,将氧枪直径和氧枪浸没深度作为研究变量,考察了侧吹射流穿透行为的影响因素和作用机理,为氧煤燃烧熔分炉侧吹炉体和氧枪设计提供理论指导。

1 回转窑预还原-氧煤燃烧熔分炼铁工艺介绍

回转窑预还原-氧煤燃烧熔分炼铁工艺流程见图1[10]。该工艺核心熔池设计采用矩形炉型,双排风口浸没式侧吹熔炼,上下排风口交错式分布,见图2。其中,氧煤燃烧熔分炉熔池区域分为2 个部分:一部分是下排风口向上区域;另外一部分是下排风口向下区域。在第一部分中,熔池区域渣铁未完全分离,以熔体形式存在,而金属相是在下排风口往下区域被完全分离。在此仅研究第一部分,将渣相处理为液相,进而研究矩形熔池中的气液两相流流动规律。

图1 回转窑预还原-氧煤燃烧熔分炼铁工艺流程Fig.1 Process flow of rotary kiln pre-reductionoxygen coal combustion melting and separation ironmaking

图2 氧煤燃烧熔分炉设计Fig.2 Design of oxygen coal combustion melting and separating furnace

2 实验原理和装置

以氧煤燃烧熔分炉为原型,采用有机玻璃制作熔分炉模型,通过改变氧枪直径和氧枪浸没深度,考察不同氧枪变量对矩形侧吹浸没熔炼熔池内射流行为变化的规律。

2.1 实验原理

在熔池喷吹进行过程中,要同时满足模型和原型的Fr和Re均相等存在很大困难,只有保持1∶1的相似比才可实现,且Re在超过自模化区规定的值后,此时Re的变化几乎不会对流场特性造成影响。除此之外,由于本工艺熔炼反应器中主要涉及气液两相流动,重力和惯性力为主要考虑因素,因此,在此选择Fr,并对其进行修正。

用水模拟渣相,空气模拟CO,为了保证熔池内射流运动的相似性,根据相似原理,采用修正的弗劳德数F′r为相似准则数,相关表达式见式(1)。

根据动力相似,实验模型和实际原型的弗劳德数相等,即得式(2)。

将式(2)代入(1)可得式(3)。

侧吹气体在管中的流速计算公式见式(4)。

联立(1),(2),(3),(4)得式(5)。

式(1)～(5)中:F′r1、F′r2分别为模型和原型的修正弗劳德数;Q1、Q2分别为模型和原型的气体流量,Nm3/h;d1、d2分别为模型和原型的氧枪出口直径,mm;ρl1、ρl2分别为模型和原型的液体密度,kg/m3;ρg1、ρg2分别为模型和原型的气体密度,kg/m3。

2.2 实验装置

通过式(1)、式(2)计算得到水模型不同侧吹流量、氧枪直径以及氧枪浸没深度的实验值。如图3所示,根据实际熔分炉尺寸,建立5∶1水模型装置,熔池液面高度需盛放到液位523 mm 处。

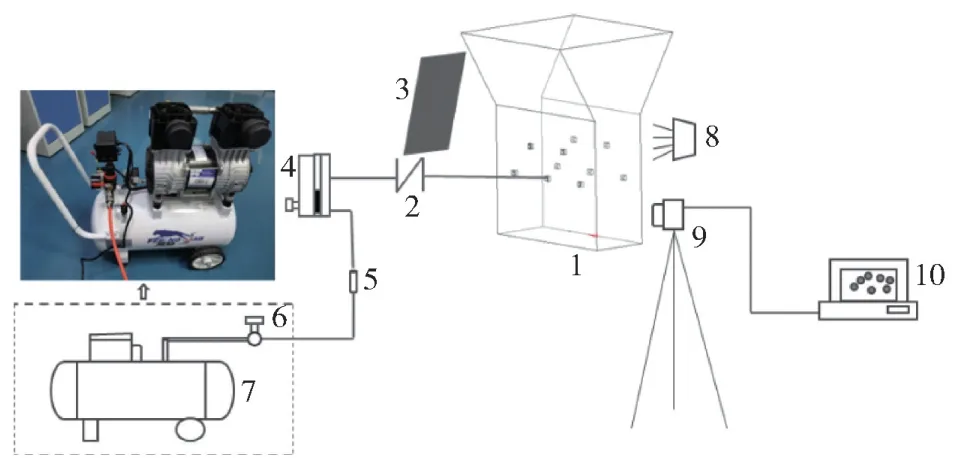
图3 氧煤燃烧熔分炉射流穿透行为实验平台示意Fig.3 Schematic diagram of experimental platform for jet penetration behavior of oxygen coal combustion melting and separating furnace

实验平台采用高速摄像机采集反应器内射流变化,并配合冷光源、空气压缩机等,将采集的图像通过Photoshop 软件结合Matlab 处理,得到射流行为相关特性参数。

3 实验结果和理论分析

气泡作为多相流动的最小单元,是衡量非稳态流体射流规律的有效途径,而射流运动的实质又可看作是单个气泡运动规律的整体表现。因此,对单个气泡上升过程的受力情况进行分析,可以实现对整体射流变化行为的理论预测。

3.1 侧吹气体射流运动模型

对射流过程中单个气泡的上升过程进行受力分析,假定气泡在静止的液体中运动,气泡的形态可近似认为是球形。气泡分别受到向下的重力FG、虚拟质量力[19]FVM、曳力Fy以及向上的浮力Ff。其中,由于受到气泡大小及形状的影响,在两相流流动的过程中,虚拟质量力远小于曳力,因此在受力分析过程中,不考虑虚拟质量力的作用。而本工艺中气泡受到的曳力体现为两相流中连续液相对气相中分散小气泡的集合所作用的力,方向与气泡和熔池中液体的相对运动方向相反,因此,将气泡的运动方向视为正方向,曳力的方向为反方向(竖直向下)。

3.1.1 单个气泡在射流内的运动模型

根据射流中单个气泡上升的受力分析情况,建立动力学方程,方向选取竖直向上为正方向,气泡的受力情况见式(6)。

分别代入各分力的表达式[20],化简得式(7)。

结合实验现象和图4,射流在上升冲击液面的同时,气泡存在匀速、加速2 个阶段,受力分析分别如下所述。

图4 射流中的气泡运动情况Fig.4 Movement of bubbles in the jet

1)匀速运动受力分析

匀速运动受力情况见式(8)。

式中:ρg、ρl、d以及重力加速度均为已知变量。

对(8)做变换,可得速度和直径的关系式,见式(9)。

式中:d为气泡直径,由于该受力模型仅对射流过程中的微小气泡进行研究,所以气泡直径较小;CD为阻力系数,由于雷诺数处于湍流区,CD取0.44;ρl、ρg分别为水和空气的密度。

选取不同梯度的小直径参数作为变量,根据式(9)可得速度随直径变化的趋势图,如图5所示。在小气泡形态中,随着气泡直径的增加,速度以近似一次函数的形式同时增加,分析可知,在湍流区域气泡群的研究范围内,相对较大直径的气泡会以更快的速度上升。

图5 气泡速度随小气泡直径的变化关系Fig.5 Relationship between velocity and bubble diameter

2)加速运动受力分析

加速运动受力情况见式(10)。

将公式(6)代入(10)得式(11)。

式中:a可以表达为

令X1=4ρgd,X2=4gd(ρl-ρg),X3=3CDρl,整理代入(11)中可得式(12)。

对式(12)进行分离变量,当t=0,u=u0,整理可得式(13)。

在t=0,u=u0时,沿竖直方向,令u0等于0,随着气泡最初受力的不平衡,气泡加速上升,根据式(13)计算可得5 种不同直径的气泡速度随时间的变化趋势图,如图6所示。由图可知,随着时间的增加,不同直径的气泡速度也在增加,最终趋于稳定,且直径越小的气泡,最终达到稳定时的速度越大。从气泡受力的角度来讲,气泡在形成初期,所受到的合力向上,浮力在合力中占主导地位,气泡加速上升。随着气泡的上升,向上和向下的合力逐渐平衡,最终速度无限接近匀速,达到受力平衡,针对本工艺,在形成射流的同时,由于所研究气泡很小,因此,气泡速度很快趋于稳定。

图6 不同直径下气泡速度随时间变化趋势Fig.6 Change trend of bubble velocity with time under different diameters

式(13)中,u可表示为其中y为小气泡上升的路程,t为气泡上升所经历的时间,当t=0,y=0,对式(13)化简、积分整理可得y关于t的数学表达式,见式(14)。

根据式(14),选取不同直径的小气泡,根据气泡加速阶段数学模型,绘制气泡上升路程y随时间的变化趋势图,以及气泡上升速度u随气泡上升路程y的趋势变化图,分别如图7、图8所示。在小气泡的研究范围中,直径越大,由于气泡体积的增加,气泡上升所经历的路程越短,从而气泡所受到的阻力越大,且气泡在熔池中的停留时间越长,此时会提升熔池中的气含率,对实际工艺来讲,更有利于气液两相的充分混合,从而强化熔池搅拌。

图7 不同直径气泡上升路程y 随时间的变化趋势图Fig.7 Change trend of rising path y with time under different bubble diameters

据图8所示,在气泡经历相同的上升路程中,气泡直径越小速度越大,运动达到稳定时的速度也就越大,速度大的气泡群冲击液面,释放动能,易引起更强烈的喷溅现象。

图8 不同直径气泡上升速度u 随气泡上升路程y 的变化趋势Fig.8 Change trend of rising velocity u with the rising path y of bubbles under different diameters

综合气泡的加速和匀速2 个阶段,气泡在射流形成的同时,先经历加速阶段,气泡加速上升,不同的直径大小的气泡会以不同的速度加速上升,最终达到稳定阶段,基于工艺所研究气泡很小,所需加速时间很短,在气泡速度达到稳定时,此时气泡竖直方向受力平衡,气泡接近匀速,冲击液面后,气泡破裂释放动能,引起搅拌。

3.2 侧吹气体射流穿透行为

氧煤燃烧熔分炉的炉型结构属于矩形侧吹浸没式熔炼炉,气体从氧枪喷入熔池后的形态变化情况如图9所示。氧枪气流随着流量的不同会形成不同形态的射流,而不同形态的射流会促使熔池搅拌体系呈现出不同的效果,如图10所示。

图9 射流形态变化示意Fig.9 Diagram of jet shape change

实验分别在不同流量工况下,选用不同评价参数对熔分炉内的射流现象进行研究。

3.2.1 射流穿透行为现象分析

针对矩形侧吹浸没式熔池工艺条件,分别选取不同直径和不同浸没深度的氧枪,通过流量的变化,探究矩形侧吹浸没式熔炼熔池内射流穿透行为的变化趋势。氧枪射流的穿透距离L在此定义为气相自氧枪口至气相出现明显上升时的距离,其中在可视化实验中,射流穿透距离的示意图如图11所示。

图11 模型穿透行为示意Fig.11 Diagram of model penetration behavior

通过综合3 组不同的氧枪浸没深度,绘制如图12所示趋势图,可知,在保持氧枪直径为4 mm 不变的情况下,随着喷吹流量的增加,侧吹射流的穿透距离近似线性增加,但不同氧枪浸没深度下,射流穿透行为的差异并不大。分析可知,当氧枪浸没深度较小时,气相在形成过程中,会更贴近壁面,在从气泡流到射流转变的过程中,部分形成的射流或气泡所带来的动能会由于“贴壁效应”造成对炉壁的冲刷作用而被消耗,进而促使射流向前喷吹的动能减小,穿透距离随即减小。但随着流量的增加,气泡流阶段缩短,气流在短时间内便可达到射流状态,此时,射流受“贴壁效应”的影响降低,因此不同氧枪浸没深度下穿透行为变化不明显。

图12 不同浸没深度下侧吹射流穿透距离趋势Fig.12 Trend of jet penetration distance under different intrusion distances

为了对4 mm 氧枪直径下的实验结果形成对比,选取氧枪浸没深度为15 mm 不变,改变氧枪的直径分别为3 mm 和5 mm,研究不同工艺流量下穿透距离的变化。

根据3 组不同的氧枪直径,绘制趋势图,如图13所示。可知,在保持氧枪浸没深度不变的情况下,射流的穿透距离继续随着喷吹流量的增加而增加,而在同一流量中氧枪直径越小,氧枪穿透距离越远。根据直径和速度流量关系可知,随着直径的减小,氧枪出口速度会增加,而出口速度的增加,会引起射流动能的增加,增强射流的穿透行为,促使射流的穿透距离相应增加。而由于氧枪直径的变化会时刻影响着氧枪出口动能的变化,因此,综合实验结果可知,在流量不变的情况下,氧枪直径对射流穿透距离的影响较大。

图13 不同氧枪直径下侧吹射流穿透距离趋势Fig.13 Trend of jet penetration distance under different oxygen lance diameters

3.2.2 射流穿透行为理论分析

为了将穿透距离和氧枪直径形成对比,基于氧枪直径对射流穿透距离影响较大的基础上,建立数学模型,进一步探究射流穿透行为和相关准则数的联系。

通过对比实验结果,在氧枪出口处射流的变化主要受到雷诺数Re、弗劳德数Fr和韦伯数We的影响。如图14所示,矩形侧吹浸没式熔炼工艺所采用的是圆管氧枪,而由于圆管氧枪喷吹在短时间、短距离内收缩现象不明显[21],因此惯性力、黏性力以及重力为主要影响因素,可忽略表面张力的影响。

图14 圆管氧枪示意Fig.14 Schematic diagram of round tube oxygen lance

综上,射流穿透距离L所表示的函数关系见式(15)。

式中:L为射流穿透距离;D为氧枪直径;g为重力加速度,取值9.8 m/s2。

根据文献[21]中所述,结合穿透距离的函数关系和影响因素,将穿透距离和氧枪直径表示为准则数的形式,见式(16)。

式中:a为系数;b、c分别为雷诺数(Re)和弗劳德数(Fr)的指数。

将式(16)转化为对数形式,见式(17)。

通过建立多元回归方程,运用Matlab 软件计算系数得:lna=-10.739;b=

因此,可得射流穿透距离表达式,见式(18)。

综上,根据射流穿透现象及理论分析结果,结合图15可知,射流穿透距离是氧枪和侧吹炉体设计的关键,针对本工艺所采用的矩形侧吹浸没熔炼熔池,喷吹流量的变化为射流穿透行为改变的主要因素;在流量恒定时,氧枪直径对穿透行为的影响相比氧枪浸没深度的影响较大;本工艺采用直管式氧枪侧吹工艺,射流入熔池时的直径可近似为氧枪直径,因此,侧吹射流穿透距离变化所引起的能量变化主要为动能转换。

图15 侧吹射流穿透情况Fig.15 Side-blown jet penetration condition

4 结论

氧煤燃烧熔分炉所采用的矩形侧吹浸没式炉型作为一种全新的无焦炼铁反应器,为钢铁领域内低碳减排问题提供了新的炼铁思路。针对矩形侧吹浸没式熔池内的射流变化,分别从射流运动模型到侧吹穿透行为进行了研究,得出以下主要结论。

1)以射流实验中单个气泡的受力情况为基础,建立射流气泡上升运动模型,在气泡匀速上升阶段,由于气泡群处于湍流区域的研究范围内,因此速度随直径呈线性增加;在气泡加速上升阶段,射流气泡直径的大小直接影响最终气泡群达到稳定时的速度变化,直径越小,达到稳定时的速度越大,进而匀速冲击液面,促使液面发生不稳定波动。

2)喷吹流量是影响侧吹穿透距离的主要因素;而在流量恒定时,氧枪直径的变化时刻会影响氧枪出口动能的变化,作用效果强于氧枪浸没深度变化引起的贴壁损耗,因此氧枪直径对穿透行为的影响相比氧枪浸没深度的影响较大。

3)综合实验结果,建立了侧吹射流穿透距离圆管氧枪数学表达式以此为基础得知,侧吹射流穿透距离变化所引起的能量变化主要为动能转换。