浅海负跃层中利用互相关输出峰值迁移曲线的声源深度判别

李晓彬 孙超† 刘雄厚

1) (西北工业大学航海学院，西安 710072)

2) (西北工业大学，陕西省水下信息技术重点实验室，西安 710072)

3) (西北工业大学，海洋声学信息感知工业和信息化部重点实验室，西安 710072)

1 引言

水下声源深度判别为发现疑似目标后的应对措施提供重要依据.不同于声源深度估计，深度判别旨在较宽容的条件下利用较少的信息对声源处于近水面还是水下进行判断.目前大多数方法是依据声源在不同深度上激发的各阶简正波的不同来分类声源，大致分为两类，一类是将接收信号中分离出的简正波模态与利用声场计算得到的模态矩阵来匹配，不同之处在于如何获取单个简正波模态.Touzé等[1]利用简正波模态的频散特性，采用时频分析的方法分离得到简正波;Nicolas 等[2]将时频分析后的信号变换到频率—波数域再得到简正波;随后，Courtois 等[3]提出利用压缩感知的方法，更好地在频率—波数域上分离各阶模态;Lopatka 等[4]发现同时利用模态的幅度和相位(符号)将得到更稳健的声源定位结果.然而此匹配场类方法容易受环境失配影响，计算得到的模态矩阵有误差，导致方法性能下降.另一类是要求声源移动较远的距离(即保证足够的水平孔径)以获取简正波模态函数并匹配的方法.Shang[5]和Neilsen[6]利用垂直阵采集到的声场模态函数的正交完备性，通过奇异值分解获得模态矩阵，并与分离的简正波模态做匹配来估计声源深度.Reeder[7]和Yang[8]通过对运动声源激发声场做Hankel 变换得到波数谱来区分水面声源和水下声源.事实上，对于声源深度判别而言，上述两类方法所使用的先分离单个模态再深度匹配的处理过程是非必须的，这是由于对声源的判别仅要求将近水面声源和水下声源区分开即可，不求解具体深度数值，无需精准匹配单个模态.

浅海负跃层的存在会使得近水面声源和跃层以下声源激发的各阶模态能量有明显差异，可以由上文介绍的分离模态方法一一反映，也可组合起来由波导不变量β反映[9，10](但这仍然要求声源相对接收阵移动).声源激发模态能量的相对大小还可以由延时求和波束形成反映[11].这是因为根据简正波理论，各阶简正波除能量不同以外，各自的俯仰角也不同.水面声源激发的高阶简正波占主导，其俯仰角较大，而水下声源低阶简正波能量占比重较大，其俯仰角较小，可以对阵列接收信号做常规波束形成(conventional beamforming，CBF)，来观察不同深度声源激发简正波的到达结构[12，13]，并基于此结构分析到达接收阵列的主导简正波，进而判别声源深度.本文借鉴文献[13]的思路，将垂直线列阵(vertical linear array，VLA)波束输出与单阵元接收信号做互相关处理，避免非脉冲声源信号的到达重叠问题，对不同时刻时延的输出取最大值并分段线性拟合，获得互相关输出峰值迁移曲线.声源深度决定了到达接收阵的主导简正波类型，其俯仰角可由曲线位于互相关时延为0 时的位置确定，依此可分辨水面声源和水下声源.互相关输出峰值迁移曲线受波导中声速随深度变化的影响较小，曲线在互相关时延为0 时刻位置的判别阈值由前几阶简正波决定，区分水面声源和水下声源的深度区间由跃层的位置和厚度决定，且跃层上下声速差越大，越有利于声源深度判别.此方法无需模态分离、声源相对垂直阵移动，也不要求精准测量声速剖面.

本文其他部分安排如下.第2 节推导了VLA的互相关输出峰值迁移曲线方程，提出了利用该曲线的声源深度判别方法，分析了水体声速随深度变化对曲线的影响，得到了曲线互相关时延为0 时刻位置的判别阈值，给出了判别算法流程图.第3 节通过仿真实验给出了本文所提方法的判别结果，深入分析了跃层参数改变对方法的影响，研究了不同信噪比条件下算法的性能，验证了方法的适用性.第4 节通过公开试验数据验证了所提方法的有效性.第5 节给出了本文得到的相关结论.

2 负跃层环境下的声源深度判别方法

2.1 垂直线列阵的互相关输出

考虑距离无关的浅海负跃层波导，采用单层海底模型，覆盖全水深的VLA 位于roz坐标系原点位置，声源位于 (rs，zs) 处.如图1 所示，rs是声源与垂直阵的水平距离，zs是声源深度，k是波数，ψ是阵列扫描角，ψn是第n阶简正波的俯仰角.

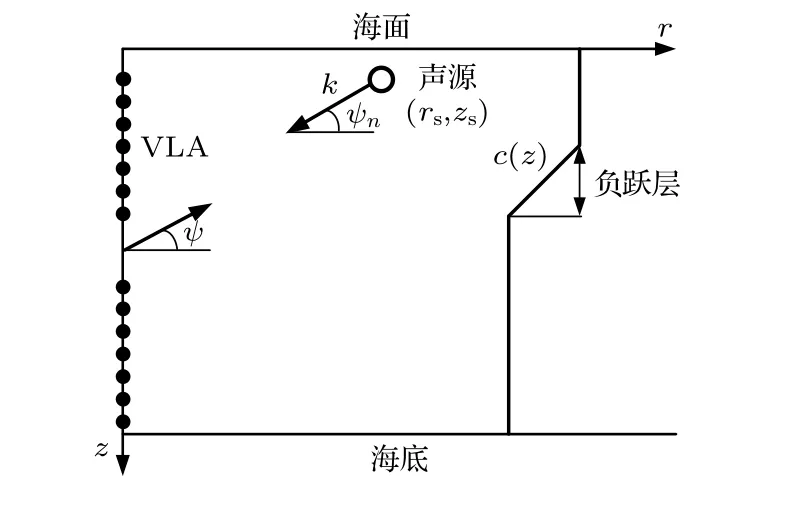
图1 VLA、声源位置和负跃层声速剖面示意图Fig.1.VLA，the position of the source and SVP in shallow water with a negative thermocline.

定义VLA 的互相关输出Iae(s，τ) 由阵列时域波束输出pa(s，t) 与任一阵元接收时域信号pe(zl，t)做互相关处理得到，是关于阵列扫描角ψ和互相关时延τ的函数

式中，s=sinψ;T为信号处理时长，zl是阵元深度，l=1，2，···，L，L是阵元个数.(1)式中的时域表达可以由阵列频域波束输出Pa(s，f) 和单阵元接收声压信号Pe(zl，f) 复共轭乘积的逆傅里叶变换得到:

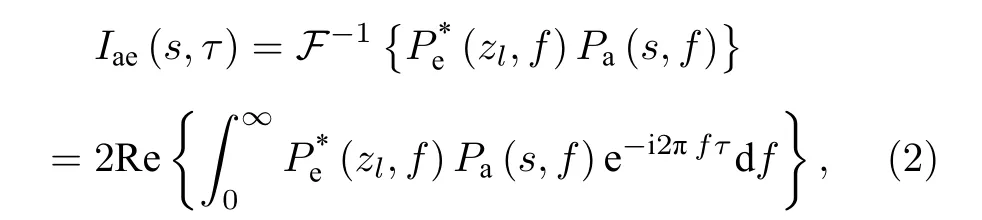
式中，F-1表示傅里叶逆变换，Re {·}表示取实部.

在远场简正波假设下，位于 (rs，zs) 位置上的点声源辐射的声压为[12]

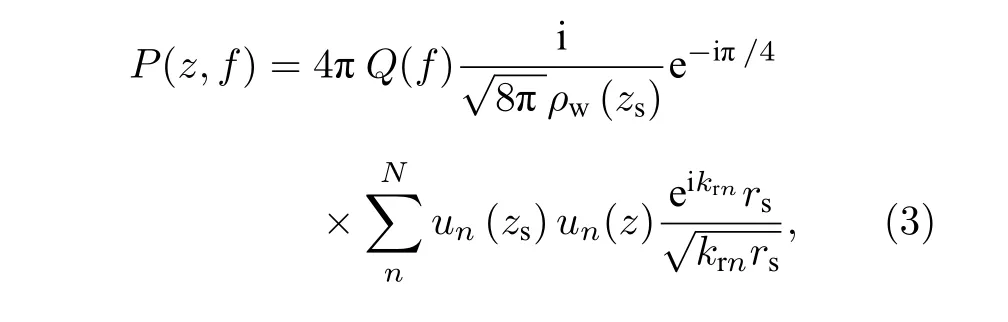
式中，Q(f) 是声源频谱;ρw是水体密度;N是声源激发简正波模态的总阶数;krn是第n阶简正波的水平波数;un是第n阶简正波的模态函数且满足，H为波导深度.VLA 对接收信号波束形成后的频域输出Pa(s，f) 可以表示为阵列扫描角ψ的函数:

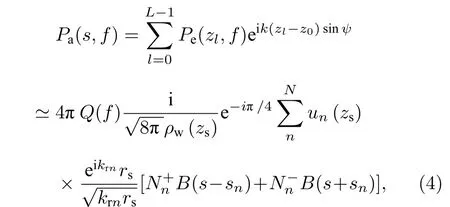
式中，sn=sinψn;是用WKB 近似将第n阶简正波模态函数表示为形式时的平面波幅值，kzn是第n阶简正波的垂直波数;B(s) 是VLA 的波束图.

将(3)式和(4)式代入(2)式可得

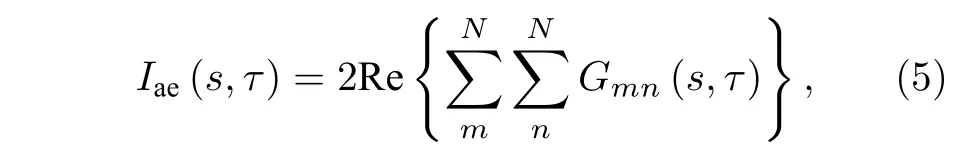
式中，Gmn(s，τ) 为Pa的第m阶模态和Pe的第n阶模态乘积的复包络

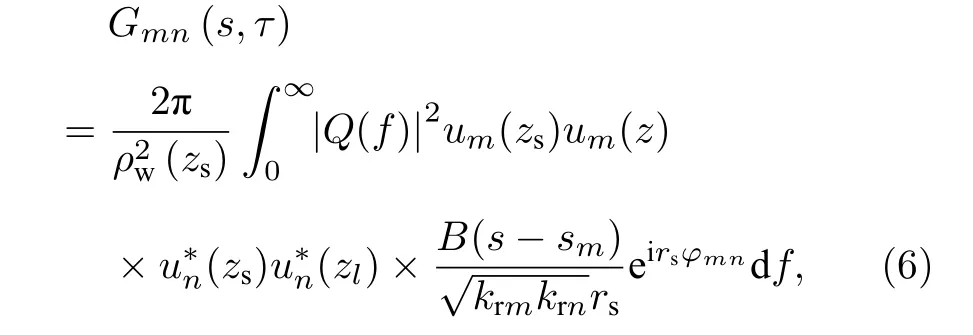
式中，φmn=(krm-krn)-2πfτ/rs.关于m=n和m/=n时的Gmn具体形式及推导见附录A.Gmn中的模态能量大小由um(zs) 和un(zs) 决定.

求解(6)式中的积分需要利用稳相法[14]，即要求φmn满足:

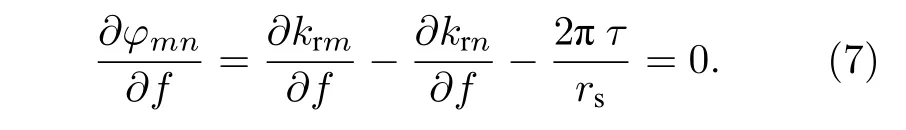
此时，恰好有互相关时延τ等于第m阶模态和第n阶模态的到达时间差τmn:

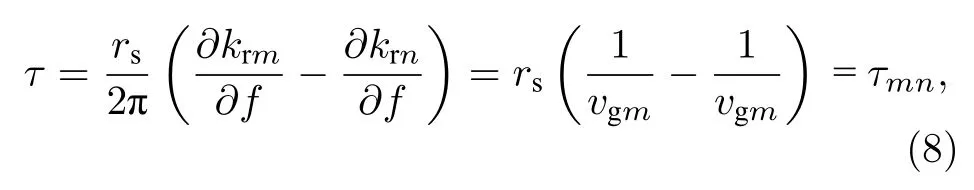
式中，vgm和vgn分别为第m阶模态和第n阶模态的群速度.

综上，Iae(s，τ) 包含了模态间的到达时间差τmn、模态俯仰角ψm和模态能量um(zs) 以及un(zs)，即显示了模态到达结构，且Iae(s，τ) 仅与声源功率谱|Q(f)|2相关，与源信号在时域上的具体形式无关.图2 展示了Iae(s，τ) 阵列指向角s＞0 (水平方向向下为正)的部分，这是由于每个简正波实际上可以表示为一个上行和下行平面波的叠加[11]，考虑一侧也可观察简正波到达结构.

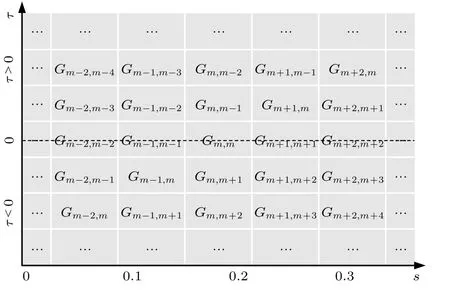
图2 互相关输出示意图Fig.2.The cross-correlation output.

由图2 可以看出:1)由于Gmm是第m阶模态自相关的形式，其位于τ=0 位置.第m阶模态的俯仰角ψm随m增大而增大，Gmm在s轴上的位置向右移 动;2)当m＞n时，vgm ＜vgn，τmn＞0，Gmn出现在τ＞0 区域，且随着n减小，τmn增大，Gmn在τ轴的位 置上移.当m＜n时，vgm ＞vgn，τmn ＜0，Gmn出现在τ＜0 区 域，且随着n增 大，τmn减小，Gmn在τ轴的位置下移.

2.2 互相关输出峰值迁移曲线

负跃层波导下，互相关输出峰值迁移曲线指的是，在τ(时延)变化时，Iae(s，τ) 在s(角度)维上的最大值连成的曲线.由2.1 节中的(5)式和(6)式可知，最大值出现在τ=τmn且s=sinψm，即互相关时延等于模态到达时间差，且阵列扫描角对准第m阶模态的俯仰角:

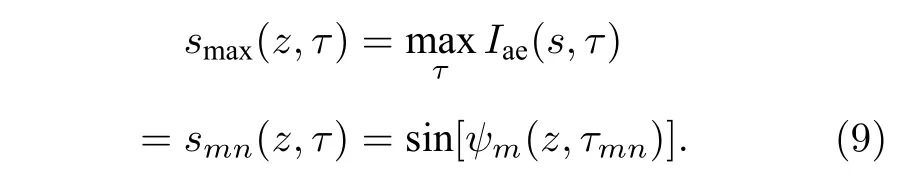
当τmn＞0 时，(9)式可以写成(推导过程见附录B):

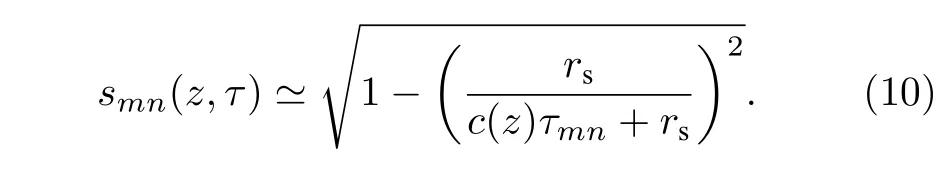
该式表明，峰值smn将随着τ的增大向右上方迁移，原因有:1)更高阶模态与第n阶模态的到达时间差更大使峰值向上移;2)更高阶模态有更大的俯仰角使峰值向右移.为方便分析，不妨假设声源激发信号经远距离传播后到达接收阵能量最大的模态是第m阶模态.依简正波理论，模态衰减系数随阶数增大而增大，这意味着第1，2，···，m— 1阶模态的激发程度远小于第m阶模态，也小于第m+1，m+2，···阶模态等，因此Gm，m-1＜Gm+1，m，Gm+1，m-1＜Gm+2，m，···，依此类 推.随 着τ的 增大，峰值将在τ维逐次向上移τmn，同时在s维逐次向右移 sinψm-sinψn，即总的来说，峰值向右上方迁移.

当τmn≤0 时，(9)式可以写成(推导过程见附录B):

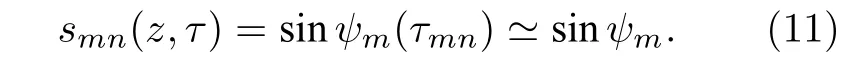
该式表明，峰值smn将随着τ的减小向下方迁移，位置仅与ψm有关.声源激发的第m阶模态能量最大，也即Gmm(s，τ)＞Gmn(s，τ)，n/=m，使得峰值在s维不会左右迁移.更高阶的第n模态与第m阶模态的到达时间差更大，峰值将在τ维逐次向下移τmn.

然而由(10)式可以看出，在负跃层环境下利用VLA 观察简正波的到达结构，还有水体中随深度变化的声速c(z) 造成的两个现象:1)不同深度上的声速不同导致同一阶模态在不同接收深度上的俯仰角不同，使得Iae(s，τ) 上出现同一阶模态具有不同俯仰角的峰裂分现象，可能影响峰值在s轴的位置;2)不同深度上的声速不同导致CBF 的相邻阵元间的延时Δ与单阶模态到达相邻阵元的时间差不匹配，使得峰值在s轴的位置发生偏移.下面对这两个现象及其对峰值位置的影响逐一分析:

1)定义相速度小于水中最大声速的模态为陷获模态[15](trapped mode，TM)，它对应前文提到的低阶模态，仅在模态函数反转点深度以下的水体中传播.定义其他模态为非陷获模态(non-trapped mode，NTM)，对应前文中的高阶模态，在全深度水体中传播.定 义kr-TM和kr-NTM分别为TM 和NTM 的水平波数，kup，ktc和kdn分别为跃层上、中和下部分的波数.图3 给出TM 和NTM 在不同接收深度上的俯仰角示意图，ψTM-tc和ψTM-dn分别为TM 在跃层中和跃层下的俯仰角，ψNTM-up，ψNTM-tc和ψNTM-dn分别为NTM 在跃层上、中和下部分的俯仰角.

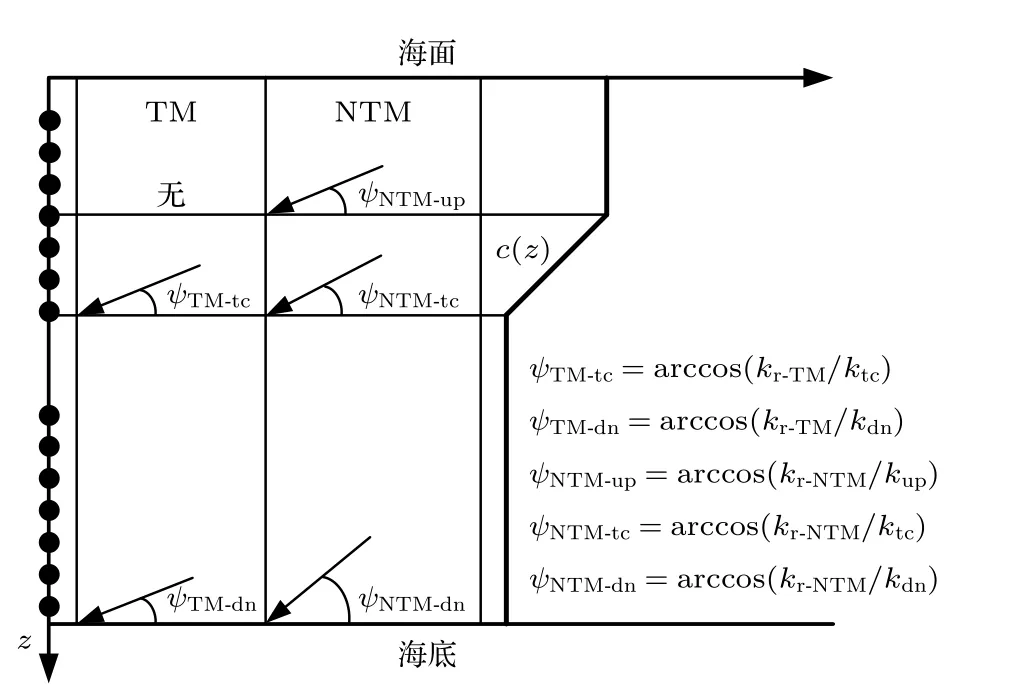
图3 TM 和NTM 在不同接收深度上的俯仰角示意图Fig.3.The elevation angles of TM and NTM at different depths.

由于跃层上和跃层中的声速比跃层下的声速大，因此kup＜ktc＜kdn.NTM 在跃层上中部分水体的俯仰角比跃层下的要小，即更靠近s=0 端，可能被误认为是较小俯仰角的TM，进而影响峰值位置.但一般地，水体跃层下的厚度大于跃层上和跃层厚度之和，这部分模态的能量多数仍集中在跃层下部分.因此对互相关输出取最大值，仍然处于跃层下的模态俯仰角处，即对峰值位置没有影响.

2)Iae(s，τ) 包含了阵列波束输出，声速不失配时CBF 的相邻阵元间的延时可以写成Δ=dsinψ/c.而负跃层水体中声速c(z) 随深度变化，这将导致互相关输出的峰值位置 sinψ产生偏差.经过简单推导可将偏差|sinψ-sinψe|写成:

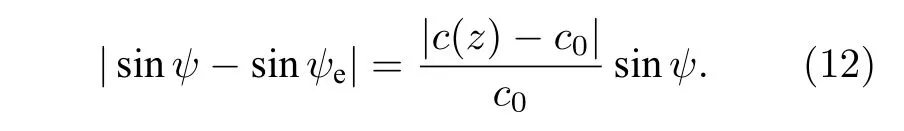
一般浅海水体中声速范围在1440—1540 m/s[16]，此处c0选择CBF 中的常见声速1500 m/s，用于判别的ψ也小于 1 0°(下文有证明)，所以该偏差最大约为0.0069.因此即使有偏移，对结果影响也极小，可以忽略不计.

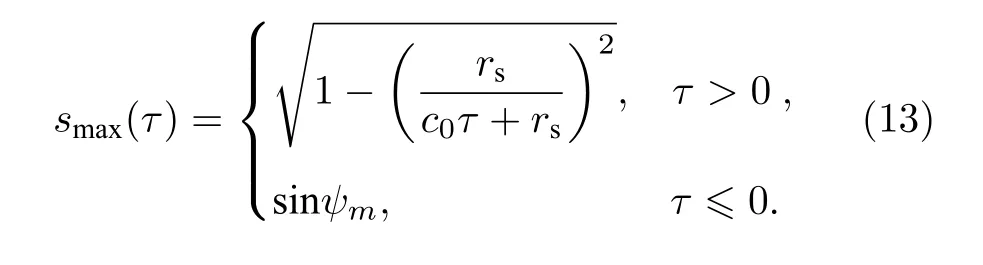
综合上述分析，将(10)式和(11)式重写如下:即为负跃层波导下的互相关输出峰值迁移方程.取Iae(s，τ) 在不同τ时刻上的峰值，按(13)式分段线性拟合，得到负跃层波导下的互相关输出峰值迁移曲线smax(τ)，如图4 黑线所示，曲线在τ=0 时的位置位于到达接收阵能量最大的第m阶模态的俯仰角处.

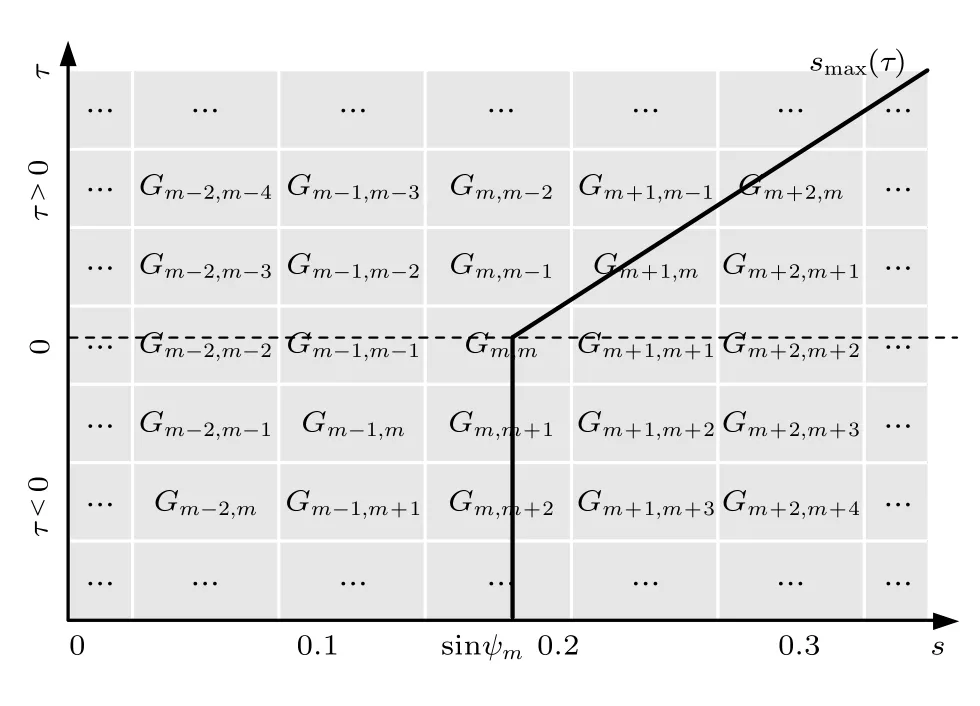
图4 互相关输出峰值迁移曲线示意图Fig.4.The peak migration line of the cross-correlation output.

2.3 声源深度判别方法

在负跃层波导中，TM 存在反转点，其模态函数在反转点以深是振荡变化的，在反转点以浅呈指数规律迅速衰减[17].水面(跃层以上)声源位于所有TM 的反转点深度以浅，激发的TM 能量极小，到达接收阵的主导简正波是NTM，互相关输出峰值迁移曲线在τ=0 的位置位于NTM 的大俯仰角处.而位于水下(跃层以下)的声源，激发的TM和NTM 能量虽然有大有小，但由于TM 远距离传播后的衰减较小，到达接收阵的能量大，TM 的小俯仰角处成为曲线τ=0 的位置.利用跃层上下声源激发的各阶简正波能量和俯仰角的不同，可以根据互相关峰值迁移曲线互相关时延为0 时刻的位置进行声源深度判别.

基于上述分析，主导简正波的类型由声源深度也即TM 的激发程度决定.这意味着，前几阶TM的俯仰角将成为互相关时延为0 时刻位置的判别阈值.第n阶简正波的水平波数krn(f) 在理想波导条件下(负跃层波导下也满足)可以表示为

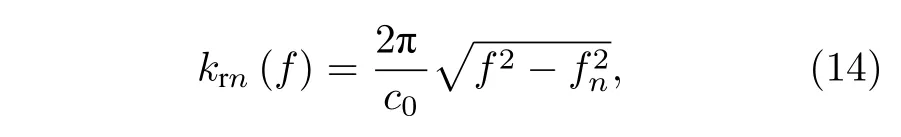
式中，fn表示第n阶简正波的截止频率，在前几阶TM 的截止频率远小于信号分析频率的条件下(也即fn/f≤0.1≪1)，可由泰勒级数得到:

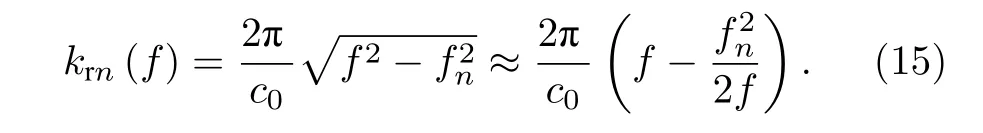
则第n阶简正波的俯仰角为

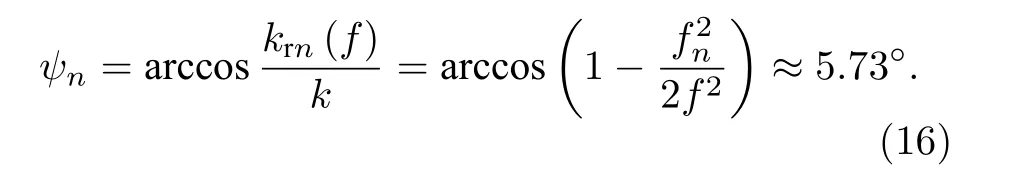
得到曲线互相关时延为0 时刻位置的判别阈值sinψn ≈0.1，依此就可以进行声源深度的判别.因此，阵列接收信号的互相关输出峰值迁移曲线的smax(τ=0)＞0.1 时即可判别为水面声源，否则为水下声源.

作为总结，图5 给出了本文提出的利用互相关输出峰值迁移曲线判别声源深度的算法流程图.

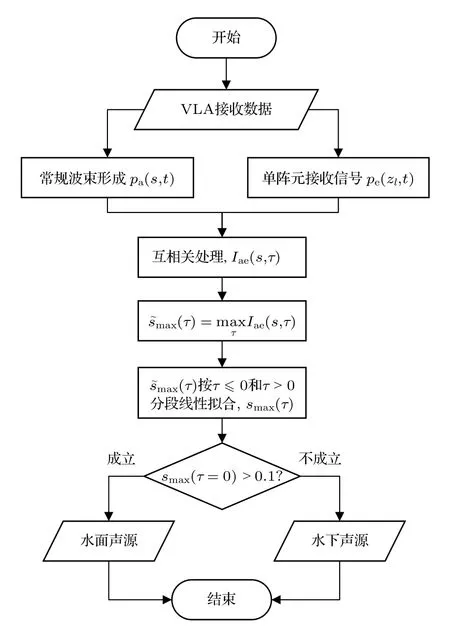
图5 判别算法流程图Fig.5.The flow diagrams of the source depth discrimination.

3 仿真实验与分析

本节将通过仿真实验验证利用互相关输出峰值迁移曲线判别声源深度方法的有效性，并探究曲线随跃层参数的变化规律及造成这种变化的物理机理，以及研究不同信噪比条件下算法的性能.仿真使用的波导环境模型和VLA 如图6 所示，图中标注了相关的海洋环境参数，负跃层波导水深100 m，跃层位于20—40 m 深度.VLA 覆盖整个水深，阵元个数L=100，起始阵元深度为1 m，阵元间距为1 m.声场与模态函数由Kraken 程序计算.

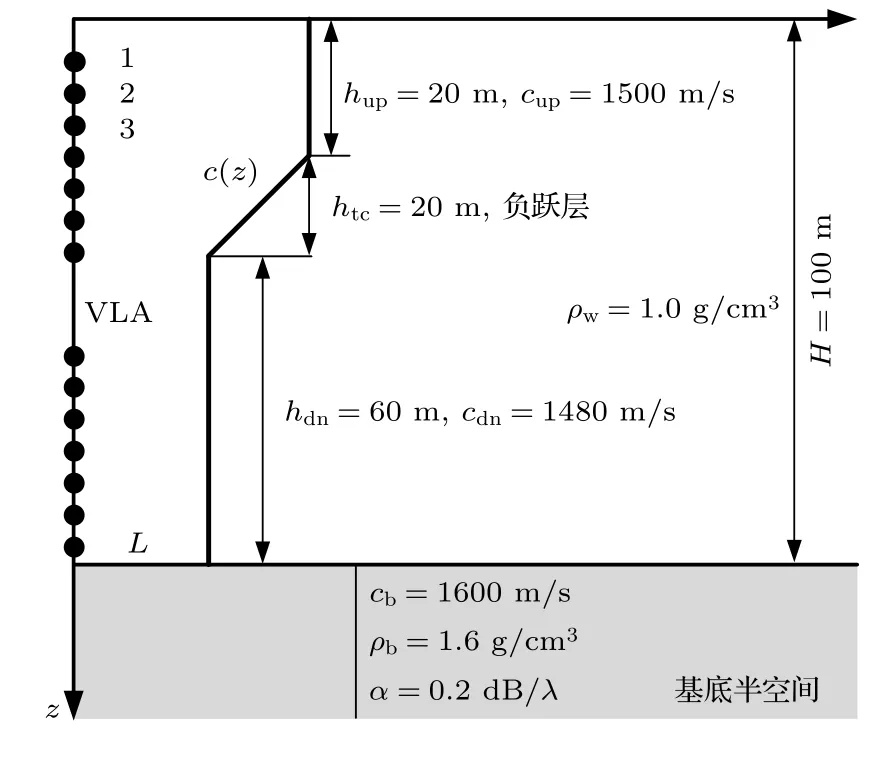
图6 负跃层波导环境及其相关参数Fig.6.The shallow water waveguide with a negative thermocline and its environmental parameters.

3.1 数值仿真

图7 给出此仿真环境下的频率400 Hz 声源激发的各阶模态函数.由图7 可以看出，位于负跃层深度以上的声源，TM 的激发程度很低，同时受到远距离传播衰减影响，到达接收处能量比重较大的是NTM 的前几阶.而负跃层深度以下的声源，TM和NTM 都有激发，同样由于衰减，到达接收阵的TM 占能量主导.

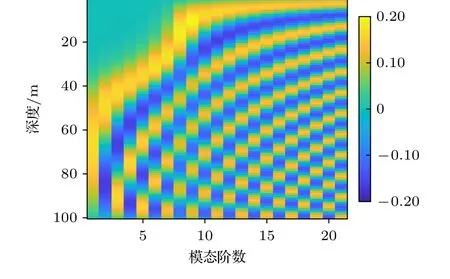
图7 各阶模态函数Fig.7.The mode functions.

假设声源深度分别为10 和50 m，声源与VLA水平距离为5 km，选取的声源信号为线性调频信号，频率范围为380—420 Hz，时长1 s.对不同深度声源的接收信号分别做CBF，再与99 m 处阵元接收信号做互相关(与任一阵元都可反映模态互相关)，得到互相关输出Iae(s，τ)，分别提取不同τ时刻上Iae(s，τ) 的最大值s˜max(τ)，并分段线性拟合，即得到互相关输出峰值迁移曲线smax(τ)，如图8 所示.

观察图8(a)发现，白色虚线圈内有能量较大的部分，这是由于位于跃层之上的声源激发的前几阶NTM 在跃层上和跃层中的俯仰角较小，且群速度稍小于TM，出现在Iae(s，τ) 的τ较小的负值位置且靠近s=0 处，对应2.2 节分析c(z) 造成的现象1)即同一阶模态具有不同俯仰角的峰裂分现象.然而在搜索最大值的过程中，同样的模态在跃层下的俯仰角更大且跃层下接收能量更大(阵列数更多)，使得最大值落在较大的俯仰角处.所以当τ ＞0 时，smax(τ) 位 于s＞0.1 .当τ≤0 时，smax(τ)仅与激发的NTM 的俯仰角有关，因此仍位于s ＞0.1 .而观察图8(b)发现，当τ≤0 时，跃层下声源的smax(τ) 位于s≤0.1 处.以上即证明了互相关输出峰值迁移曲线用于声源深度判别的有效性.

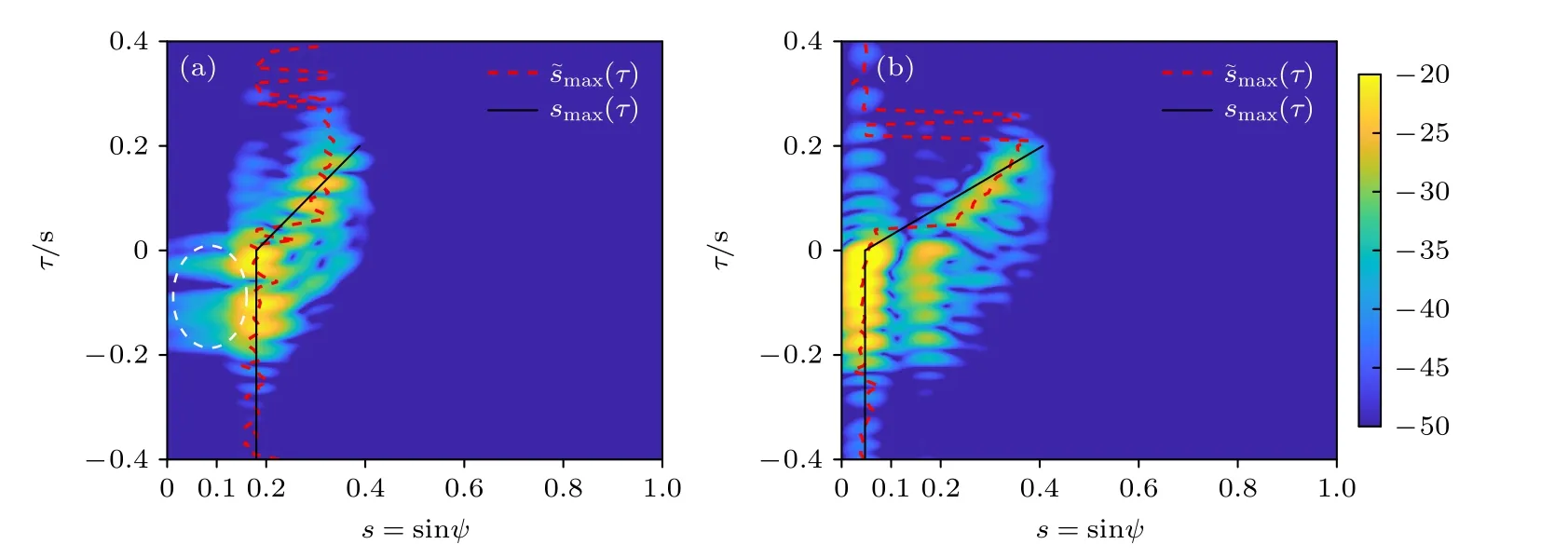
图8 不同声源深度的 Iae(s，τ)，s ˜max(τ) 和 smax(τ) (a)声源深度10 m，白色虚线圈标注了峰裂分现象;(b)声源深度50 mFig.8.Iae(s，τ)，and smax(τ) of sources at different depths:(a) Source at a depth of 10 m，with the peak splitting indicated by white dashed circle;(b) source at a depth of 50 m.

3.2 跃层参数对曲线位置的影响及机理分析

对于激发TM 极小的水面声源来说，其互相关输出峰值迁移曲线的smax(τ=0) 位置将在所有TM 的俯仰角以右，因此决定其位置的是TM 的数量及其占激发简正波总数的比例(一般地，声源激发的简正波总数受声源频率和水深影响最大，环境参数变化对其影响较小).而TM 数量与跃层参数相关，这就使得互相关输出峰值迁移曲线会受到跃层参数的影响.

为充分说明跃层参数不同时对曲线的影响，这里给出跃层厚度变化、跃层起始深度变化和跃层上下声速差改变时的理论分析结果，以及跃层上下声速差改变时的示例.除声速剖面和跃层外其他环境参数与3.1 节示例相同.TM 临界数n*可以写成[18]:

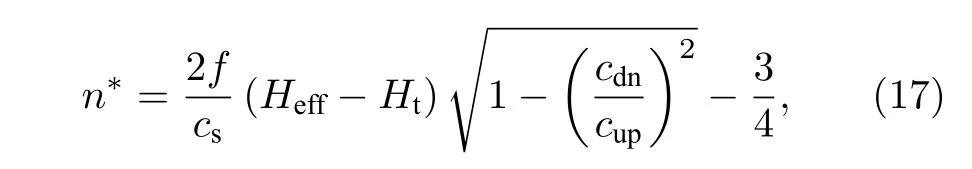
式中，cs是水面的声速;Ht是反转深度;cdn是跃层下的声速;cup是跃层上的声速;等效深度[19]Heff可以写成:

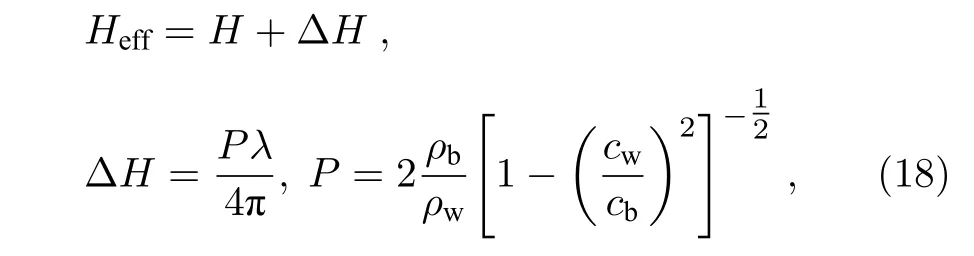
式中，P为反射系数的相位参数;ρb为海底底质密度;ρw为水体密度;cw为水底声速;cb为海底底质声速.将(18)式代入(17)式可得

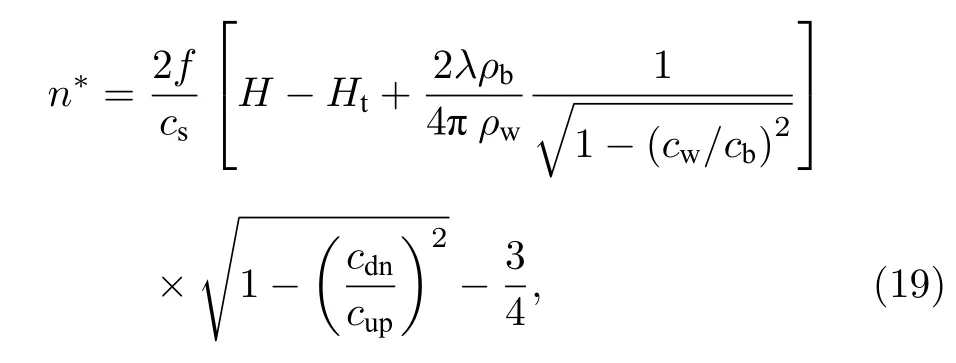
式中，TM 的临界反转深度Ht为跃层起始深度，cw=cdn.由(19)式可知，影响TM 的临界数n*的参数主要有声源频率f，跃层起始深度Ht，跃层下声速cdn和海底底质声速cb.

单独改变跃层厚度htc，临界数n*没有变化，本文所提方法有效且能完全区分开跃层上下的声源.当htc=0 m 时，此时波导变为理想负跃层波导，仍存在有反转点的TM.当htc变大时，也仅改变了判别声源来自水面还是水下的深度范围.

单独改变跃层起始深度Ht，对临界数n*的影响较小，本文所提方法仍然有效.起始深度变浅，TM 的反转深度变浅，比起始深度更浅的声源会被判别为水面声源.起始深度变深，TM 的反转深度也变深，此时只有比跃层下界更深的声源才会被判定水下声源.

固定跃层厚度htc、跃层起始深度Ht和跃层上声速cup不变，将跃层上下声速差 Δc由前文中的20 m/s(1500—1480 m/s)变为0 和40 m/s，得到其他条件相同时的模态函数和处理结果如图9 和图10 所示.由(19)式简单推导可知，跃层上下声速差减小到0 时，波导变为等声速波导，n*为负数，说明此时已没有TM，水面声源和水下声源都将激发低阶和高阶简正波，曲线互相关时延为0 时刻位置均位于s＜0.1，本文所提方法失效，如图10(a)和图10(b)所示.跃层上下声速差 Δc变大，cdn和cw都减小，(19)式中因子位于加法计算使n*变小，而因子位于乘法计算对临界号数的影响更大，最终使n*变大即TM占总体简正波的比例增加.因此互相关输出峰值迁移曲线将整体右移(对比图8(a))，如图10(c)所示，更有利于声源深度判别.

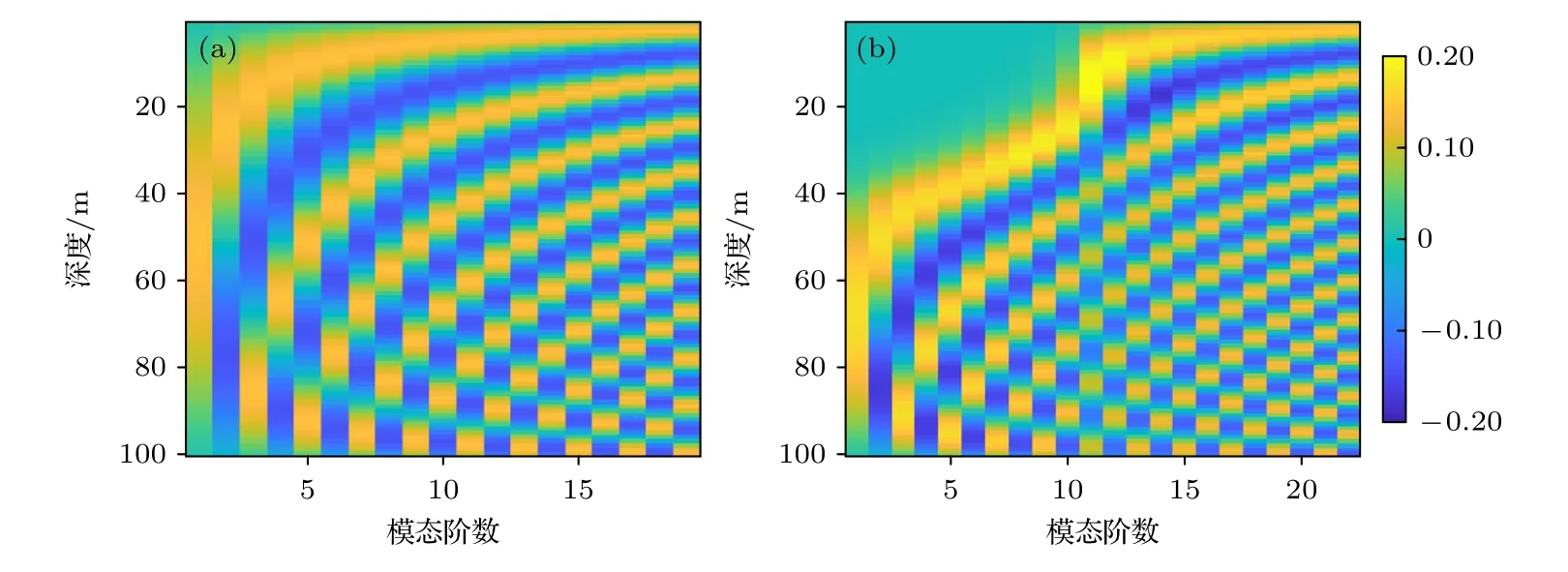
图9 不同声速差时的各阶模态函数 (a) Δ c=0 m/s;(b) Δ c=40 m/sFig.9.The mode functions with different Δ c :(a) Δ c=0 m/s;(b) Δ c=40 m/s.

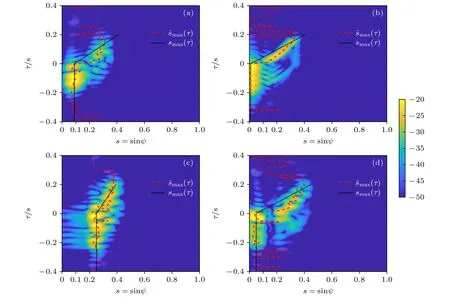
图10 不同声速差时不同声源深度的 Iae(s，τ)，和 smax(τ) (a) Δ c=0 m/s，声源深度10 m;(b) Δ c=0 m/s，声源深度50 m;(c) Δ c=40 m/s，声源深度10 m;(d) Δ c=40 m/s，声源深度50 mFig.10.Iae(s，τ)，and smax(τ) of sources at different depths with different Δ c :(a) Δ c=0 m/s，source at a depth of 10 m;(b) Δ c=0 m/s，source at a depth of 50 m;(c) Δ c=40 m/s，source at a depth of 10 m;(d) Δ c=40 m/s，source at a depth of 50 m.

3.3 不同信噪比条件下判别方法的性能

本小节通过改变不同输入信噪比条件，研究所提判别方法的性能.除信噪比设置外，其他仿真条件与3.1 节设置相同.定义输入信噪比为各阵元接收信号功率的平均与阵元噪声功率的比值:

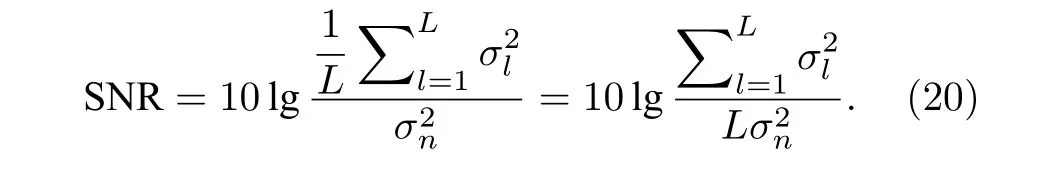
图11 给出了SNR 分别为—10，—20 和—25 dB下 的Iae(s，τ)，s˜max(τ) 和smax(τ) .由 图11(a)—(d)可以看出，在SNR=—10 和—20 dB 时，尽管信噪比较低，仍能从图中提取互相关峰值迁移曲线有效进行声源深度判别.这是由于利用覆盖全水深的VLA 接收信号做波束形成已经获得了相当的阵增益，得到输出后再与单阵元接收信号做互相关处理，相当于匹配滤波操作，进一步获得了一定处理增益.当SNR 进一步降低(—25 dB)，互相关输出Iae(s，τ)已完全被噪声主导，如图11(e)和图11(f)所示，提取出的互相关输出峰值轨迹混乱，无法拟合有效的峰值迁移曲线smax(τ)，也无法判别声源来自水面还是水下.图11 结果表明，利用所提方法判别声源深度，需要保证一定的SNR，在阵元极低SNR 条件下，方法性能下降甚至无法有效判别.

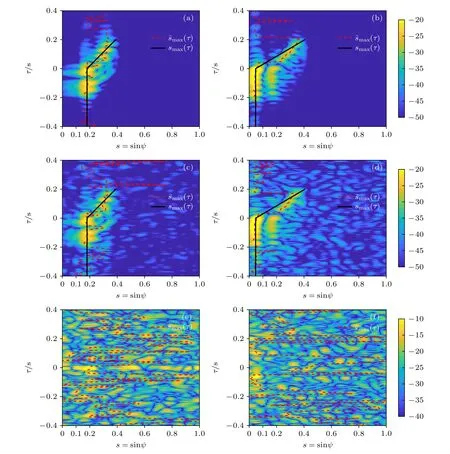
图11 不同SNR条件下，不同声源深度的 Iae(s，τ)，和 smax(τ) (a) SNR=—10 dB，声源 深度10 m;(b) SNR=—10 dB，声源深度50 m;(c) SNR=—20 dB，声源深度10 m;(d) SNR=—20 dB，声源深度50 m;(e) SNR=—25 dB，声源深度10 m;(f) SNR=—25 dB，声源深度50 mFig.11.Iae(s，τ)，and smax(τ) of sources at different depths with different SNR:(a) SNR=—10 dB，source at a depth of 10 m;(b) SNR=—10 dB，source at a depth of 50 m;(c) SNR=—20 dB，source at a depth of 10 m;(d) SNR=—20 dB，source at a depth of 50 m;(e) SNR=—25 dB，source at a depth of 10 m;(f) SNR=—25 dB，source at a depth of 50 m.

4 海试数据分析

本次海试数据是来自SWellEX-96 水声试验[20].本文采用试验S5 部分的数据对所提深度判别方法的有效性进行验证.

图12(a)展示了S5 试验的阵列布放位置及发射船拖曳声源的航迹(蓝色方格为船只每5 min 的位置).VLA 布放在航迹西北方向处.试验场海底有23.5 m 的沉积层，覆盖在800 m 厚的泥岩层上，声速剖面细节如图12(b)所示，可以近似看作负跃层波导环境.发射船拖曳了“浅”声源(J-13，9 m 深)和“深”声源(J-15，54 m 深)，各自的频率如表1 所示.依给出的VLA 阵元间距(6 m 左右)选取合适的处理频率范围100—170 Hz，此频带内，J-13 声源有109，127，145 和163 Hz 四个频率成分，J-15声源有112，130，148 和166 Hz 四个频率成分，采样频率为1500 Hz.

表1 不同声源的频率Table 1.Frequencies transmitted by different sources.

图13 是依实验波导环境仿真的135 Hz 的简正波各阶模态函数图，图中用黑线标出深度9 m和54 m.再结合图12(b)可以看出，J-13 声源位于负跃层以上，而J-15 声源位于跃层靠近下端位置，可以近似为负跃层以下，考虑使用本文所提方法进行声源深度判别.

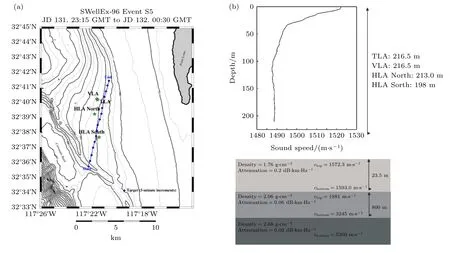
图12 S5 试验情况 (a) 试验场环境与发射船轨迹;(b) 声速剖面Fig.12.Event S5:(a) The environment and the track of the source ship;(b) SVP.

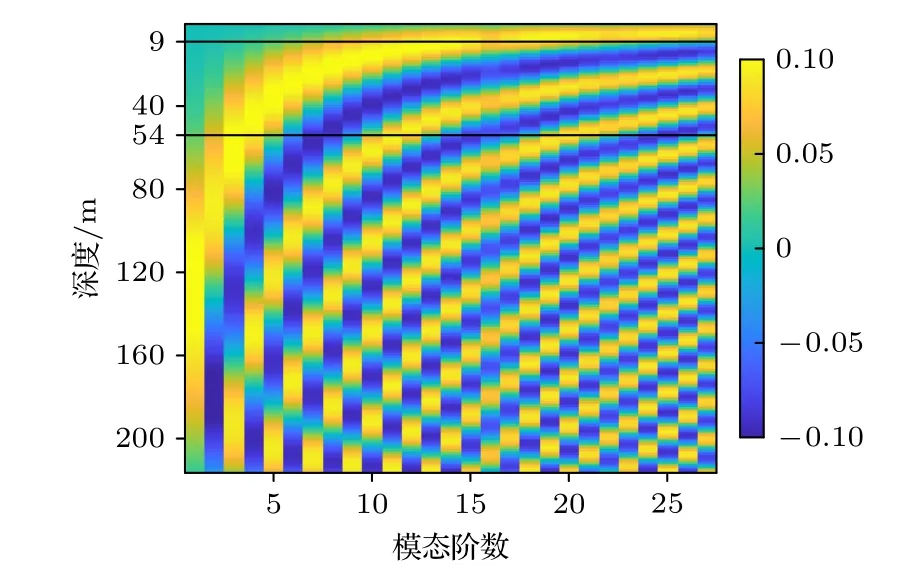
图13 S5 试验波导下频率135 Hz 的各阶模态函数Fig.13.The mode functions in S5 waveguide with f=135 Hz.

取VLA 第2700—2701 s 接收数据分别滤除水面声源频点和水下声源频点后做CBF，与第1 号阵元(深度212.25 m)第2700—2701 s 的接收信号做互相关处理得到输出和互相关输出峰值迁移曲线如图14 所示.在S5 试验水文条件下，仿真计算可以得知135 Hz 激发的前8 阶简正波为TM，且 第9 阶模态 的俯仰角为ψ9=13.43°，sinψ9=0.23 .从图13 也可以看出，声源位于深度9 m 处激发的TM 能量极小.因此J-13 声源的互相关输出峰值迁移曲线的smax(τ=0) 在0.2 附近(如图14(a)所示)，可以判断为水面声源.而J-15 声源位于54 m 深度，处于除第1 阶外的其他所有TM 的反转深度以下，因此其互相关输出峰值迁移曲线的smax(τ=0) 在0.1 附近(如图14(b)所示)，可以判断为 水下声源.

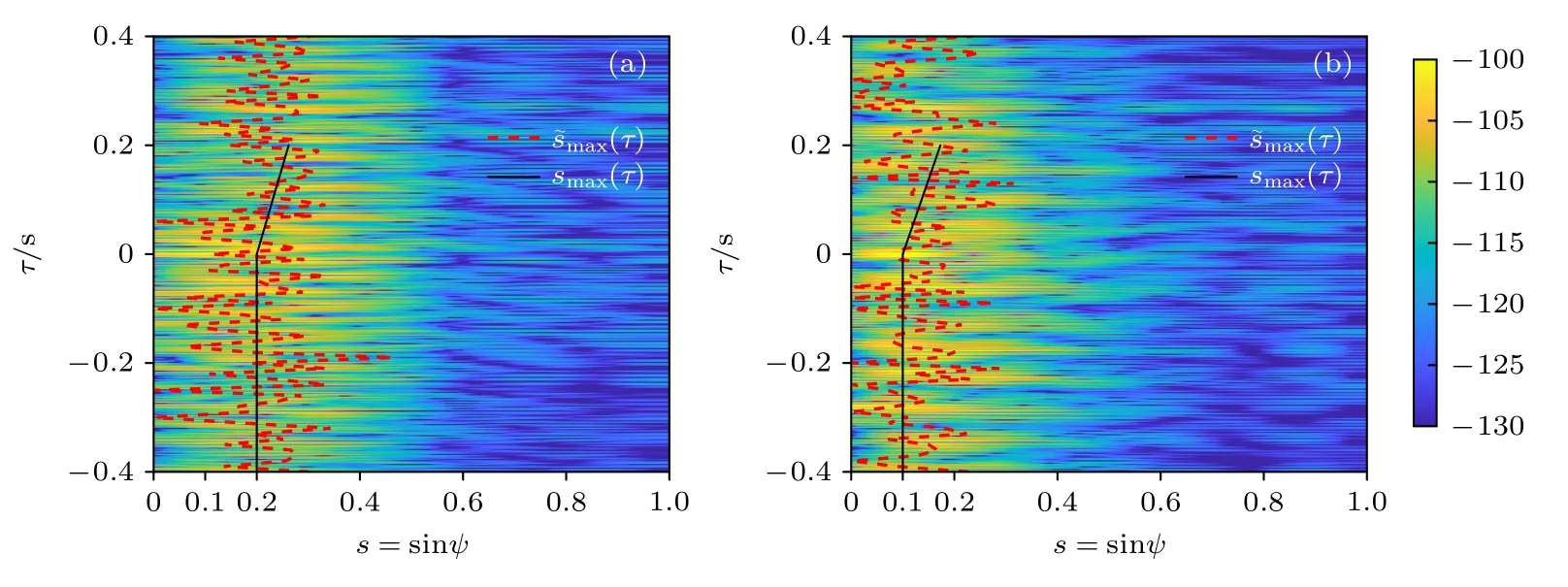
图14 J-13 和J-15 声源的 Iae(s，τ)，s ˜max(τ) 和 smax(τ) (a)J-13，9 m;(b)J-15，54 mFig.14.Iae(s，τ)，and smax(τ) of different sources:(a) J-13，9 m;(b) J-15，54 m.

5 结论

本文研究了浅海负跃层波导中的声源深度判别，根据声源激发各阶简正波模态的能量和俯仰角不同，提出了一种利用互相关输出峰值迁移曲线的声源深度判别方法.通过理论分析、仿真实验与海试数据验证得到了如下结论:1)方法利用垂直阵波束输出与单阵元接收信号的互相关输出来观察简正波的到达结构，互相关峰值迁移曲线反映声源激发简正波的相对大小.方法无需分离模态、声源相对接收阵移动，也不要求对声速剖面的精准测量;2)曲线受负跃层波导中声速随深度变化的影响较小，曲线互相关时延为0 时刻位置由声源信号到达接收阵的主导简正波的俯仰角决定;3)曲线互相关时延为0 时刻位置的判别阈值由声源激发的俯仰角较小的前几阶陷获简正波决定;4)跃层的位置和厚度决定了声源所属的深度区间，且跃层上下声速差越大越有利于声源深度判别.

附录A

对于m=n，Gmn可以写成:

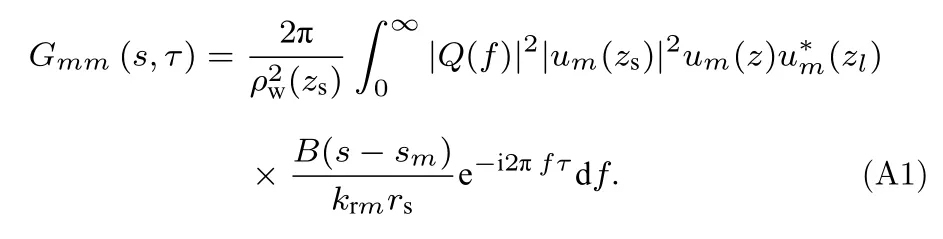
在τ=0 时，Gmm是第m阶模态自相关的形式.

对于m/=n，Gmn可以由稳相法近似成:

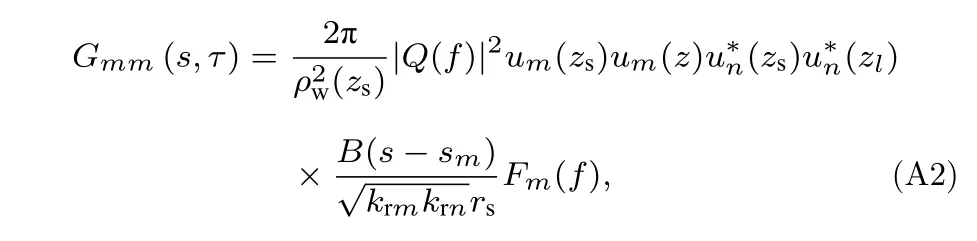
式中，Fm(f) 是利用稳相法得到的与相位有关的函数:

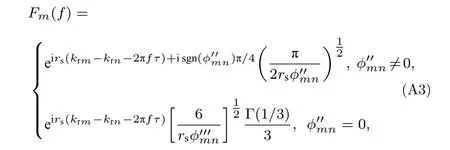
式 中，sgn {·}为符号函数;分别表 示对函 数φmn求关于f的二阶导函数和三阶导函数;Γ (·) 为Gamma函 数.

附录B

在水平分层波导中，简正波模态的群速度和俯仰角的关系[12]为

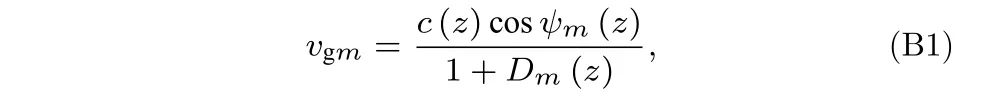
其中Dm(z)=[c(z)/2π]sinψm(z)[dkzm(z)/df] .对于大多数远离截止频率的简正波而言，Dm(z) 可以忽略.

当τmn＞0 时，此时m＞n，n取1 方便推导，cosψn ≃1，s inψn ≃0，Dn(z)≃0 .代入(B1)式有

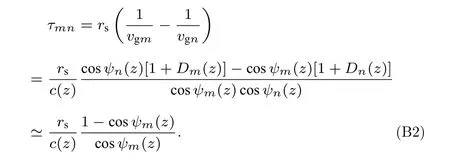
再根据(9)式和(B2)式得到:

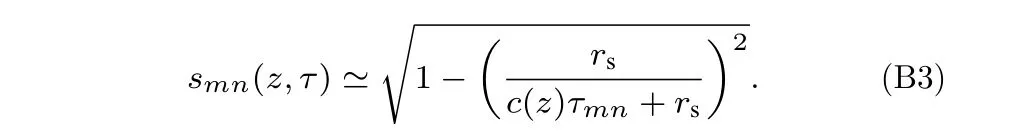
当τmn≤0 时，此时m≤n，一般都有更高的第n阶模态与第m阶模态的到达时间差更大，使曲线向下迁移.同时由于声源激发的第m阶模态能量最大，使得曲线不会左右迁移.因此有