利用脉冲延迟实现微波波导中量子态存储与异地按需读取*
朱道泉 项玉 孙风潇† 何琼毅2)
1) (北京大学物理学院,人工微结构和介观物理国家重点实验室,北京 100871)
2) (北京大学,教育部纳光电子前沿科学中心,北京 100871)
1 引言
以量子物理为基础的量子信息技术,在保障信息安全、提高运算速度、提升测量灵敏度等方面具有巨大的潜力.其中,量子存储是量子信息处理的关键步骤[1-5],是未来拓展量子通信应用[6,7],实现量子计算[8-10],建立大尺度量子网络[11-13]等量子信息前沿应用的核心技术之一.随着量子技术的加速发展,各类量子信息处理任务对量子存储的要求也越来越高.以量子计算为例,为了实现更大规模的集成通用型计算线路,需要将不同节点处的量子处理器连接起来进行分布式量子计算提升对量子态的处理能力[14-16].这不仅要保证每个节点处对量子态进行长时间、高保真的存储,还需要实现量子态在不同节点之间的高保真传输[7,17-20]与按需读取[20-29].所谓按需读取,是指量子态写入存储器以后再根据需求决定读出的时间,这为更大的量子通信或计算单元实现同步操作提供可能.比如,2020 年中国科学技术大学首次实现了按需式读取的可集成固态量子存储器[27].
目前,人们已经在多种物理体系中对量子存储进行了深入的研究,在单个原子[30]、原子系综[7,12,20,31-39]、光学腔[40-42]、微波腔[19,25,43,44]、固态体系[4,21-24,26,29,45-51]、混合体系[28,52,53]等物理体系中已经实现了量子态存储.大多数的研究工作中量子态的写入与读取操作是在同一节点处进行,再将量子态传输到另一节点,存储与传输是两个分开的过程.而在超导体系中,微波波导既可以设计为高品质因子的微波谐振腔,作为量子存储器进行量子态存储[25,43],又可以作为微波传输线实现量子态传输[17-19],因此基于微波波导可以将两个过程结合起来.比如,已经有实验利用单一微波谐振腔同时实现了单量子比特的量子态存储与传输[43],这里为了实现量子态存储,波导长度需要设计为其谐振波长的一半.进一步,2021 年清华大学采用超导多谐振器的动态调控与微波传输线相结合的结构,首次在实验中实现了对单光子水平微波脉冲的存储与按需读取[25].那么,是否可以简化模型,利用单一波导实现量子态的高保真存储和按需读取,同时解除对波导长度的设计限制,对此我们在下面进行了初步的理论探讨.
一种可能的方案是利用受激拉曼绝热路径(stimulated Raman adiabatic passage,STIRAP)将待传递的量子态编码到体系的暗态上[54],这样可以将量子态绝热地从一个模式通过中间的微波波导传输到另一个模式[55,56].进一步,我们在原始STIRAP方案的基础上在两个控制脉冲之间引入延迟,使得它们分别作用在波导两端作为写入与读出脉冲,将输入量子态存储到中间的微波波导中.具体的,考虑图1 所示的由两端超导谐振腔和中间微波波导构成的量子电路模型.两端的谐振腔分别作为量子态的写入和读取单元,中间的波导用来存储和传输量子态.以存储高斯态为例,我们采用正弦波形脉冲,通过设计写入与读出脉冲的持续时间以及二者的延迟时间,数值模拟后发现写入脉冲的持续时间在一定范围时,一旦量子态在波导中的存储时间超过某一临界值,在之后的任意时刻都可以施加读出脉冲对量子态进行读取,在理想条件下读出量子态的保真度可高达0.999.这样就可以根据任务需求决定读出时间,实现量子态的异地高保真按需读取.并且,通过对比相同保真度下的脉冲持续时间可以看出,本方案可以将脉冲面积降为原始STIRAP方案的三分之一,消耗能量更少.最后,考虑到体系暗态与外界解耦,因此量子态受波导模式耗散与噪声的影响很小,可以保持较稳定的量子态存储.据此,我们对结果进行了鲁棒性分析,证实本方案对中间波导中的平均热光子数和读取脉冲的持续时间具有较强的鲁棒性.
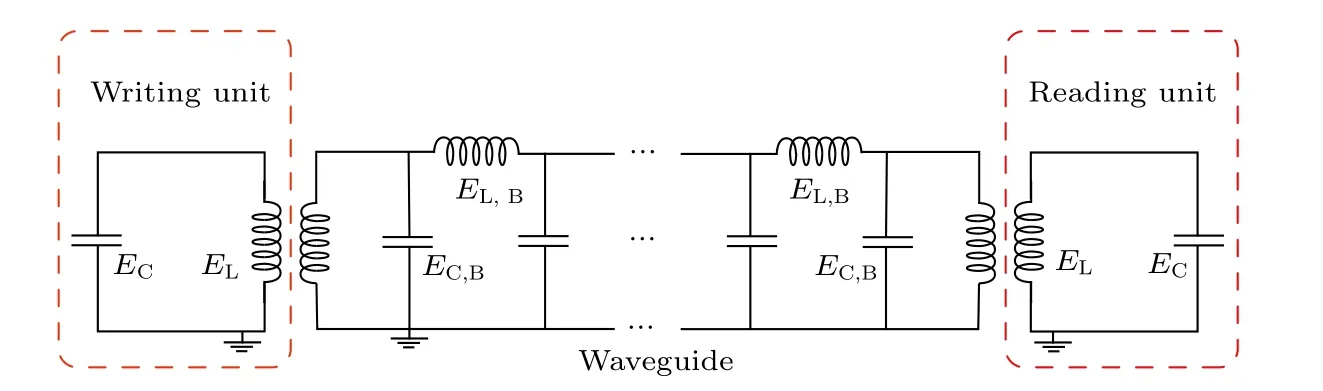
图1 量子态存储与异地读取方案图.EC,EL 分别代表两端读写腔的电容充电能和电感能量.EC,B 和 EL,B 为波导中每个单元的电容充电能和电感能量Fig.1.Setup for quantum state storage and remote retrieval.EC,EL are the capacitive and inductive energies of both writing and reading cavities,respectively.EC,B and EL,B are the capacitive and inductive energies for the unit cell within the waveguide.
2 体系模型
2.1 离散波导模型
本文对位于中间的波导采用离散化模型[57]描述,把波导看成 2N0+1 个单元(N0≥0),每一个单元包含1 个电容和1 个电感.这样在正则量子化后,1 个单元可以用1 对共轭算符来描述.设波导单位长度的电容为cB,单位长度的电感为lB,每个单元的长度为x.则每个单元的电容的充电能为EC,B=e2/(2cBδx),电感能量为,其中Φ0=ℏ/(2e),为约化磁通量量子.整个波导的哈密顿量为
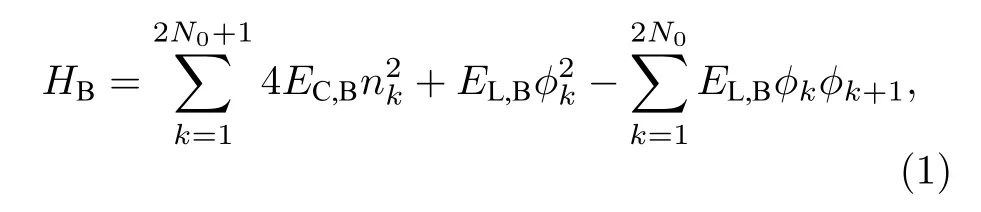
式中,无量纲电荷算符nk和磁通量算符φk构成一组共轭算符,满足对易关系 [φk,nk]=i.理想波导需要满足连续性极限假设[58],即 2N0+1→∞,且波导长度d固定,这就要求每个单元的长度δx=d/(2N0+1)→0 .在这一极限下,我们可以得到波导中的色散关系为

2.2 体系的演化方程
谐振腔与波导之间通过互感相互作用耦合,体系的总哈密顿量可以表示为

式 中:EC=e2/(2C) ,EL=Φ02/L,C,L分别为 微波腔的电容和电感强度;M是波导与微波腔的互感强度;下标 0 代表写入腔,下标 2N0+2 代表读出腔.需要注意的是,哈密顿量的半正定性要求M≤从(3)式中可以得到两微波腔的频率为ω=,我们根据这一频率对系统中的所有时间ti、频率ωi进行无量纲化处理,即ti →ωti,ωi →ωi/ω.
一般而言,体系的维度随着模式个数的增加会指数增长,数值求解多体系统的完整动力学演化是比较困难的.对于某些量子态,我们可以通过计算其不同阶矩来对体系进行刻画,这样就使得系统维度由原本的指数增长降为多项式增长.因为体系哈密顿量的形式是关于所有共轭算符的二次型,所以如果体系的初始量子态为高斯态,那么体系将一直处于高斯态上.这样我们只需获得其一阶矩和二阶矩就足够对体系进行完美刻画.接下来,我们就以高斯态为例,研究它在体系中的传输规律.
首先对于共轭量 {(φi,ni),i=0,1,2,···,2N0+2},可以定义如下的场算符矢量v=[φ0,φ1,···,φ2N0+2,n0,n1,···,n2N0+2]T.其一阶矩与二阶矩可以被表示为
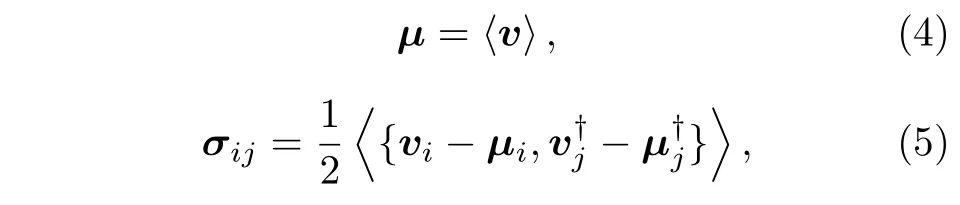
式中,〈·〉代表期望,{A,B}=AB+BA,为反对易子.场算符矢量v所满足的动力学方程为线性方程
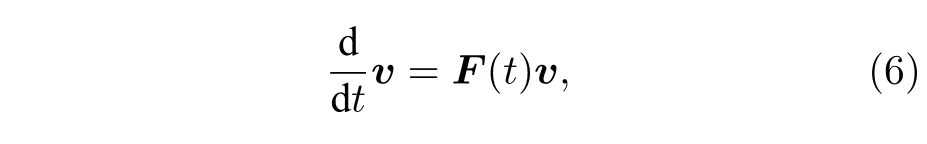
式中,F(t) 表示v的演化矩阵.通过海森堡方程,我们可以确定F(t) 的各个矩阵元,

由(6)式可以得到v的前两阶矩的运动方程分别为
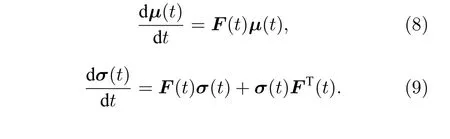
3 量子态存储与按需读取的理论方案
3.1 受激拉曼绝热路径
首先对原始的STIRAP 做一个简单介绍.对于1 个Λ型三能级体系,我们可以通过施加两束控制光ΩP和ΩS,分别控制 1↔2 与 2↔3 之间的 跃迁.在旋波近似、双光子共振的条件下,体系的哈密顿量为
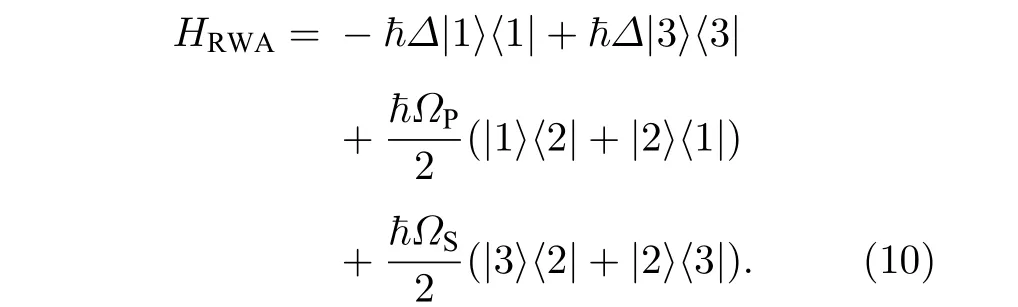
其中取|2〉 能 级能量为零,Δ为|1〉、|3〉 能级与|2〉 能级之间的跃迁频率.通过求解体系的本征能量,可以发现该体系存在1 个仅由|1〉 和|3〉 构成的暗态|dark〉=cosθ|1〉 -sinθ|3〉,其中tanθ=ΩP/ΩS.根据绝热定理,如果系统初始时刻处于系统哈密顿量的本征态上,那么当系统进行绝热演化时,系统将一直处于该本征态上.因此通过缓慢调节脉冲,使其由初始时刻的ΩP(0)≪ΩS(0) 缓慢变化到末时刻的ΩP(tf)≫ΩS(tf),可以将体系从|1〉 绝热地演化到|3〉 .需要指出的是,STIRAP 方法不仅对三能级体系适用,也适用于三模式系统,使其中A 模式的量子态绝热地传递到与之不相邻的C 模式中,且对中间模式B 的耗散鲁棒[55,56].
3.2 基于改进的STIRAP 方案实现量子态按需读取
在原始STIRAP 的方案中需要全过程施加脉冲,导致其脉冲能量利用率比较低.因此我们需要对STIRAP 进行一定的改进,希望仅仅通过简单的脉冲调控就能提高能量利用率并实现量子态的按需高保真读取.考虑到波包在波导中传播需要一定的时间,我们这里在原始STIRAP 方案中的两脉冲之间引入时间间隔 ΔT,得到本方案中的写入脉冲ΩW(t) 和读出脉冲ΩR(t)

式中,A为脉冲的最大幅值,T为脉冲持续时间,ΔT为读出脉冲的可控延迟.
为了刻画读取出量子态的保真度,这里采用基于写入和读出量子态的Wigner 函数的保真度定义[59]
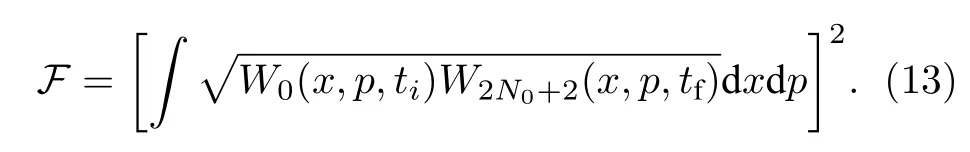
在 2N0+1=11,A=0.1ω,且波导中热光子数为零的条件下,数值遍历所有的T和 ΔT的取值,我们得到如图2 所示的结果,可以看出,图中存在1 个可用于量子态长时间高保真存储的区域.在该系统参数取值下,主要数值模拟结果已经收敛,因此可认为 2N0+1=11 已经近似满足连续性极限假设.图中所有的时间、频率都以读写腔的频率ω进行了无量纲化.
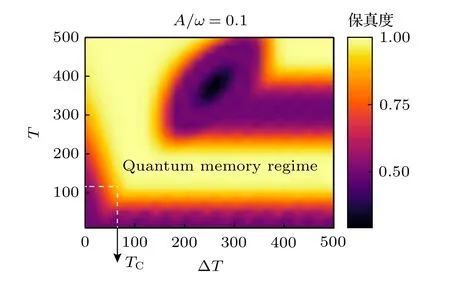
图2 读出量子态与写入量子态之间的保真度随着读写脉冲持续时间 T、读出脉冲延迟 Δ T 的变化关系图.这里的读出脉冲与写入脉冲最大强度均为 A=0.1ω .图中所有的时间、频率都以读写腔的频率 ω 为参考进行无量纲化.当脉冲写入时间满足 1 00/ω ≲T ≲200/ω 时,读出脉冲可以在临界时间 TC 之后的任意时刻对量子态进行高保真读取Fig.2.The fidelity of the scheme as a function of the duration of the pulse T and the delay of the reading pulse Δ T .The amplitudes of both the writing and reading pulse are A=0.1ω .Each frequency and time scale in this figure are normalized by the bare frequency ω of the writing/reading cavities.One can notice that once the duration of the writing pulse satisfies the condition 1 00/ω ≲T ≲200/ω,highfidelity quantum state retrieval is possible after the critical time TC .
基于图2 的结果,可以发现:1)当 ΔT=0 时我们的方案就回归到原始的STIRAP 方案(实现态传递,但未实现态的存储),可以看出,它只在脉冲持续时间足够长(T≳500/ω)的时候才能实现量子态读出的保真度大于0.999;2)基于我们改进后的STIRAP 方案,当脉冲持续时间满足 100/ω≲T≲200/ω时,延迟时间 ΔT只需大于某一临界时间TC,此后的任意时刻读出量子态的保真度都可以大于0.999.这与中间模式为单一模式时的情况截然不同.当中间模式为单一模式时,读出脉冲与写入脉冲之间的大的延迟时间会严重破坏体系的绝热性质,导致体系发生非绝热演化,从而无法实现有效的态读取[54].
根据(11)式和(12)式,脉冲面积正比于脉冲持续时间.比较获取相同保真度时,原始STIRAP(ΔT=0 时)所需的脉冲持续时间为T~500/ω,而本方案中考虑波导中传输时间引入脉冲延迟(以ΔT=400/ω为例)所需的脉冲时间为T~150/ω,对比发现,后者所需的脉冲能量大约为前者的三分之一.需要注意的是,以上结果是在不考虑体系耗散的理想情况下得到的,考虑微波波导谐振腔的品质因子很高,可高达 1 06~108[17,60],因此我们这里考虑的存储时间 ΔT远小于体系的相干时间,这意味着耗散不会对上述结果造成显著影响.
接着,根据图2 的结果,选择脉冲持续时间为T=150/ω,两脉冲之的延迟为 ΔT=400/ω,我们在图3 中展示写入和读取量子态的Wigner 分布,以及相应的写入和读出脉冲波形及延迟.以初态为压缩态相干态|ψ(0)〉=S(r)D(α)|0〉=|α,r〉为例进行数值计算.其中平移算符与压缩算符分别为参数取值分别为,r=0.5 .这里a†和a是正则量子化后得到的产生、湮灭算符,即φ=φZPF(a+a†) ,n=nZPF×i(a-a†),其中φZPF=(2EC/EL)1/4,nZPF=[EL/(32EC)]1/4分别为磁通量和电荷的零点振荡.图3(a)和图3(b)分别为写入和读出量子态在相空间的Wigner 准概率分布,通过(12)式计算得到量子态的保真度为0.9997.图3(c)展示了写入脉冲ΩW(t) 和读出ΩR(t) 脉冲波形.
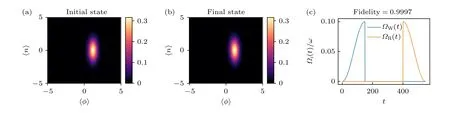
图3 量子态的存储与读取结果展示 (a)和(b)分别为写入量子态与读出量子态的Wigner 准概率分布;(c)所需写入脉冲与读出脉冲的波形以及量子态的读取保真度.参数取值分别为:T=150/ω,Δ T=400/ω,A=0.1ωFig.3.Numerical results for the storage and the retrieval of a quantum state in a waveguide:(a) and (b) are Wigner distributions of the initial state and the final state,respectively;(c) shows the pulses of our protocol used for storing and retrieving the quantum state.The related parameters are T=150/ω,Δ T=400/ω,A=0.1ω .
在原始STIRAP 中要求初始时刻ΩW(0)≪ΩR(0),末时刻ΩW(tf)≫ΩR(tf),而本方案的脉冲不满足上述条件,因此接下来我们对本方案量子态读取的鲁棒性进行研究.在图4 中,我们固定脉冲 .延迟 ΔT=400/ω,写入脉冲时间T=150/ω.图4(a)和图4(b)分别考虑了保真度与中间波导模式的平均热光子数Nth以及读出脉冲的持续时间T2之间的关系.从图4(a)中可以看出,保真度对于波导中的平均热光子数有较强鲁棒性,在热光子数大约为80 时保真度仍然保持在0.90 左右.图4(b)中的结果同样展示出保真度对于读出脉冲的时间具有较强鲁棒性,随着读写脉冲持续时间差别|T -T2|的增大,保真度发生缓慢下降,当这一差别|T -T2|为写入脉冲持续时间T的一半时,保真度依然大于0.90.因此我们的方案可以实现鲁棒、高保真的量子态存储与按需读取.
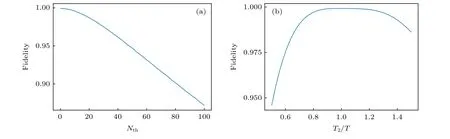
图4 量子态保真度的鲁棒性.将写入腔的初态制备在1 个压缩态|ψ(0)〉=|α,r〉,其中 α=,r=0.5 .(a)和(b)分别展示了保真度对微波腔中平均热光子数,以及对读出脉冲持续时间的鲁棒性.参数取值分别为:写入脉冲持续时间 T=150/ω,读出脉冲延迟 Δ T=400/ω,脉冲的最大幅值 A=0.1ωFig.4.Robustness of the fidelity for the retrieval of the quantum state.The initial state in the writing cavity is prepared to be asqueezed coherent state|ψ(0)〉=|α,r〉 with α= and r=0.5 .(a) and (b) show the robustness of the fidelity against the average number of thermal photons inside the waveguide and the duration of the reading pulse,respectively.Here we fix the duration of the writing pulse T=150/ω,the delay of the reading pulse Δ T=400/ω and the maximum amplitude for both pulses A=0.1ω
4 结论
本文在STIRAP 方案的基础之上,通过设计正弦波形写入脉冲的持续时间,并对读出脉冲引入可控延迟,实现了量子态在微波波导中的长时间存储与异地高保真按需读取.以体系初态制备在高斯态为例,我们的结果表明,在理想条件下量子态在波导中存储时间达到某一临界值之后,可以在任意时刻施加读出脉冲读取量子态,且保真度高达0.999,由此实现了对量子态的高保真按需读取.并且,所得到的保真度对波导中的平均热光子数、读出脉冲的持续时间都有较好的鲁棒性.这些结果展示了利用微波波导作为中间模式进行量子态存储与读取的优越性.目前还有一些开放性问题值得后续继续研究,比如,这里展示的结果是针对高斯态,对于非高斯态,基于波导的方案是否依然能够保持很好的鲁棒性;将处于纠缠态的某一方利用该方案存储并传输到异地,是否仍然可以保持良好的纠缠特性,进而实现基于纠缠的各种量子任务;尽管高品质的微波波导腔耗散小,不会对现有理想条件下的结果造成显著影响,但考虑未来实验实现的可能性,依然需要进一步考虑实际物理体系的各项参数,以及与环境耦合导致的耗散等因素,为方案的具体实施提供进一步理论依据.

