高维宇称-时间对称系统中的信息恢复与临界性*
曲登科 范毅 薛鹏
1) (东南大学物理学院,南京 211189)
2) (北京计算科学研究中心,北京 100084)
3) (中国人民解放军陆军步兵学院,石家庄 050083)
1 引言
量子力学要求封闭系统的物理可观测值由具有实特征值的厄密算子表示.然而在自然界中,由于耗散现象的普遍存在,不可避免地存在能量、粒子以及信息等物理量的丢失,物理量的守恒性会被破坏.因此真实的物理系统实际上是非厄米系统.近年来,非厄米系统及其动力学特性越来越受到人们的关注[1-20].研究量子系统与环境之间的相互作用是至关重要的,此相互作用可以导致耗散、衰退和退相干等现象.值得一提的是如果系统满足宇称-时间对称性,则一类非厄米哈密顿量可以具有完全为实数的本征能量[21-23].非厄米哈密顿量的本征能量为实数的一个充分条件是哈密顿量满足宇称时间对称性,并且哈密顿量的本征函数同时是宇称-时间对称算子的本征函数.满足宇称-时间对称性的非厄米系统包含两个相区域:宇称-时间对称性保持的区域,在此区域内整个本征谱都为实数,在宇称-时间对称性破坏的区域本征值形成复共轭对的形态.在这两个相区间存在着奇异点,在奇异点处会有非常规的相变发生[24].
在增益和损耗平衡的经典系统已经预测和观察到宇称-时间对称系统的几个独特的性质[25-32].自从第一次在光学系统中观测到宇称-时间对称性破坏和功率振荡[25,26]以来,研究人员相继报道了非守恒系统中独有的丰富的波的现象,如单向性[30]和多功能设备中的光传输[27].相关现象已经在物理学的其他子领域进行了研究,包括电路[28]和机械振荡器[29].在量子体系中,同样研究了宇称-时间对称系统的各个方面[33-43],如玻色-哈伯德二聚体[33]、纠缠[34]以及临界现象[39-42].
虽然损耗通常被认为会对系统的相干性产生损坏[44,45],但是满足宇称-时间对称性的经典系统中的独特的现象和有用的应用说明了平衡增益和损耗的作用.从经典系统的研究成果来看,满足宇称-时间对称性的量子系统有望显示出对退相干的鲁棒性,可能会导致量子信息处理中的长相干时间.近年来,满足宇称-时间对称性的系统的信息论表征开始被探索[40-42,46].除了实际的重要性之外,这种信息论表征对于更深入地理解宇称-时间对称系统可以作为开放量子系统是必备的.在开放量子系统中宇称-时间对称的非幺正动力学的一个典型的例子就是系统与环境之间信息流动的可逆-不可逆的临界性[46].
在2019 年,中国和日本的研究小组利用两能级的光学系统,借助量子态间的可区分性量化信息的流动,实验上验证了当系统处于宇称-时间对称相区域时,流入环境的信息可以完全恢复[40].当系统自发破坏宇称-时间对称性时,信息的流动是不可逆的.同时,在宇称-时间转变点周围信息的流动具有独特的临界性,通过该点时,可逆的信息变得不可逆,反之亦然.然而对于宇称-时间对称系统的量子信息的可逆性的学习目前还限于二维希尔伯特空间的系统中,在本文中,将重点介绍在高维希尔伯特空间中,在宇称-时间对称性保持的相区域,损失到环境中的信息仍然可以完全恢复,在靠近奇异点区域时,量子态间的可区分性会出现幂律的行为.我们使用量子态间的可区分性这一物理量统一量化了低维与高维量子系统与环境之间的信息流动.
宇称-时间对称系统中的信息恢复为更好地控制量子系统的行为提出了新的可能性,其方式不同于量子芝诺效应[47-49]或动态解耦[50-52].动态解耦依赖于脉冲注入的时间反转,而本文中的信息恢复是有对称性保护的隐藏的纠缠伙伴引起的.这其中潜在的物理本质上不同于无退相干的子空间,在无退相干的子空间中,幺正态的演化由一定的对称性保持[53-59];相比之下,在宇称时间对称性保持与破坏的相区域,宇称-时间对称的动力学过程本质上都是非幺正的.本文第2 节会介绍信息流动的定义.第3 节回顾两维希尔伯特空间中信息流动的恢复与临界性.第4 节介绍高维希尔伯特空间中使用量子态间的可区分性来衡量信息的流动.最后对全文进行总结与展望.
2 信息流动
控制的动力学可以由下式表示[60]:

这里,通常使用希尔伯特-施密特内积.考虑一个通用的N能级量子系统,并根据同一系统的两个量子态之间的迹距离来表征进出系统的信息流动[61]:

马尔可夫演化问题的主要解决方法是可以基于可除性[66,69,74,75]、态的可区分性[67]、量子纠缠[69]、量子费舍尔信息流动[76]、保真度[76]、互信息[70,77]、几何表征[78]等物理量.但并不是所有的物理量都可以很好地量化表示宇称-时间对称的动力学,由于非线性的原因,可除性等物理量就无法探测宇称-时间对称系统的动力学的非马尔可夫性.然而,量子态之间的可区分性仍然可以作为宇称-时间动力学中的非马尔可夫性的一种度量,因为这种度量可以直接量化系统与环境之间的信息流动,从而检测记忆效应的存在,即使动力学是非线性的.虽然采取其他的测量方法也是可行的,由于迹距离区分了所有不同的量子态,并且只取决于系统的动力学,因此迹距离非常适合作为信息流动的测量方法.
非马尔可夫性起源于本征态的非正交性.为了解释这个,对(1)式表示的宇称-时间对称的动力学进行本征分解:

其中,|φn〉是本征能量为En的右本征矢.当动力学过程是幺正过程时,本征态是相互正交的,由(3)式的分母给出的归一化因子始终是一个常数.在宇称-时间对称的动力学过程中,归一化因子由于本征态的非正交性而振荡,表明系统与环境之间存在连续的信息交换.在这一方面,在各种系统中观测到的功率振荡可以解释为信息从环境中回流的证据[25-28,44],以及在宇称-时间对称性保持的相区域的非马尔可夫特征.
3 二能级系统中的信息恢复

值得一提的是,在量子系统中使用单光子实现宇称-时间对称的动力学演化的难度在于无法实现单光子的增益.已有实验通过更少损失与更多损失的交替来替代宇称-时间对称动力学中的增益与损失,从而实现了满足宇称-时间对称的量子系统的动力学演化过程[37].基于这种思路,该二能级系统的哈密顿量对应的有效非厄米的哈密顿量可以写为

图1(a)和图1(b)给出了在宇称-时间对称的区域(0<a <1)量子态之间的可区分性随时间的演化.作为对比,也给出了幺正演化(a=0)的情况.从图中可以看出,量子态间的可区分性随时间会出现一个周期性振荡的现象.这也意味着存在一段时间区域,在此时间中量子态间的可区分性的一次导数是大于 0 的.因此,系统恢复了流入环境的信息,在宇称-时间保持的相区域展示了独特的非马尔可夫行为.并且从图1(a)和图1(b)可以看出,振荡的时间周期随着系统逐渐靠近奇异点的位置也逐渐上升.

图1 在宇称-时间对称的两能级系统的信息流动 (a),(b) 在宇称-时 间对称保持的区域(0 <a <1),量子态的可区 分性表现出周期性振荡,当逐渐靠近奇异点(a=1)时,信息恢复的周期会变长;(c) 在宇称-时间对称性被破坏的区域(a >1),量子态的可区分性在一直在衰减Fig.1.Information flow in the parity-time-symmetric twolevel system:(a),(b) The distinguishability oscillates with period in the parity-time-unbroken phase (0 <a <1).When approaching the exceptional point (a=1),the period of the information retrieval.(c) The distinguishability between quantum states is declining in the parity-time-symmetry-broken regime (a >1).
图1(c)给出了在宇称-时间对称性被破坏的相区域(a>1)的量子态间的可区分性随着时间的演化.可以看出,可区分性随时间呈现指数衰减的趋势.若使用函数D(t)=D(0)e-t/τ对数据进行拟合,其中D(0) 为常数,τ为弛豫时间,可以发现弛豫时间随着系统接近奇异点而增加[40].在奇异点的位置(a=1),可区分性在长时间限制内可以表现出幂律的行为.如图2 所示,将计算的数据使用函数xt-y进行拟合,可以得到量子态间的可区分性展示出的幂律行为是D(t)~t-2,这与解析结果是完全符合的[46].
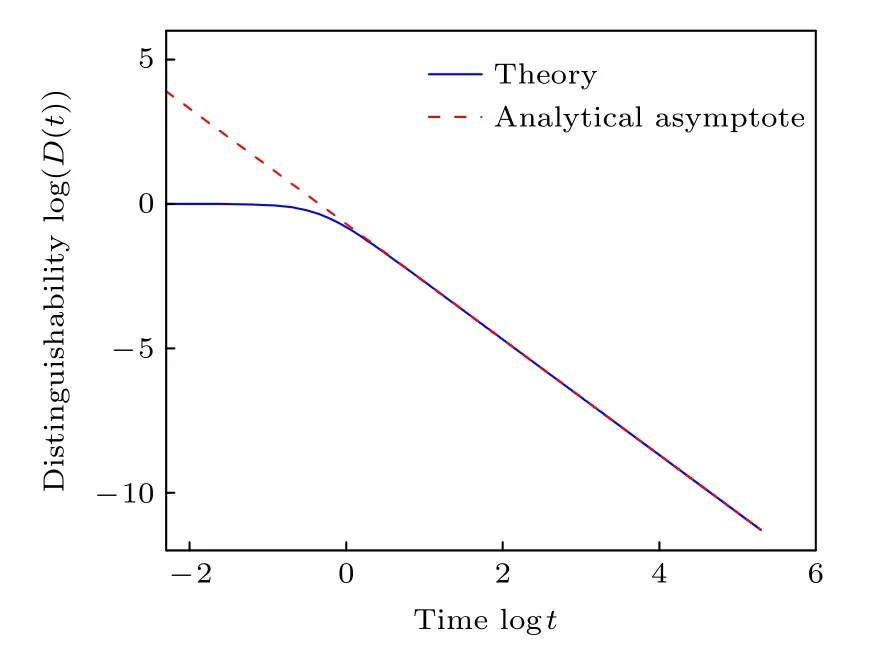
图2 在宇称-时间对称的两能级系统在奇异点处(a=1),量子态的可区分性的幂律行为Fig.2.Power-law behavior of the distinguishability of the parity-time-symmetric system at the exceptional point a=1 .
4 四能级系统中的信息恢复
对于满足宇称-时间对称性的系统的研究,还大多停留在二维希尔伯特空间中.本节主要介绍在四维希尔伯特空间中宇称-时间对称的动力学的信息恢复.考虑一个四能级的宇称-时间对称系统[41,80-82],其由以下哈密顿量描述:

其中和为SU(2)群的自旋— 3/2 表示.该哈密顿量写成矩阵表示为

该四能级系统的基态为计算基 {|1〉,|2〉,|3〉,|4〉}.该哈密顿量与反线性的宇称-时间算符对易,其中宇称算符为antidiag(1,1,1,1) 且时间反演算符由它的复共轭给出.(7)式中前两个计算模代表增益,后两个计算模代表损失.宇称-时间对称哈密顿量的本征能 量可以 表示为λk={-3/2,-1/2,+1/2,,(k=1,2,3,4),在γ=J的位置产生四阶奇异点,表示有 4 个本征值与 4 个本征态都是简并的.该宇称-时间对称的哈密顿量的能量间隙为,因此在γ<J时,系统位于宇称-时间对称性保持的相区域,在γ>J时,系统的宇称-时间对称性被打破.为了衡量在四能级系统中 的信息流动,选择初 态ρ1=1/2(|1〉+|2〉)(〈1|+〈2|) 和ρ2=1/2(|3〉+|4〉)(〈3|+〈4|) .依 然可以通过通过(2)式计算两个态随时间演化的可区分性.
如图3(a)和图3(b)所示,选择参数J=1,对于系统处于幺正演化的情况(γ=0),量子态之间的可区分性始终为 1,也就意味着系统的信息没有流失.在宇称-时间对称性保持的相区域(γ<J),与二能级系统中展示的宇称-时间对称的动力学过程相同,量子态之间的可区分性呈现出周期性振荡的现象,这种现象也标志着系统流入环境的信息会完全恢复.随着系统逐渐逼近奇异点,振荡的周期也是逐渐变长,并且信息恢复的程度也在变大.图3(c)表示量子态之间的可区分性随着时间的增加一直在衰减.当接近奇异点时,量子态的可区分性渐进地表现为D~1/t2.如图4 所示,在奇异点的位置(γ=J),量子态之间的可区分性在长时间的演化后表现出幂律行为.将计算结果使用函数xt-y进行拟合,可以得到在奇异点处,量子态的可区分性表现出的幂律行为是D~1/t2.

图3 宇称-时间对称的四能级系统的信息流动 (a),(b) 在宇称-时间对称保持的区域(γ <J),量子态的可区分性表现出周期 性振荡,当逐渐靠近奇 异点(γ=J)时,信 息恢复的周期会变长;(c) 在宇称-时间对称性被破坏的区域(γ >J),量子态的可区分性在一直在衰减Fig.3.Information flow in the parity-time-symmetric fourlevel system:(a),(b) The distinguishability oscillates with period in the parity-time-unbroken phase (γ <J).When approaching the exceptional point (γ=J),the period of the information retrieval.(c) The distinguishability between quantum states is declining in the parity-time-symmetrybroken regime (γ >J).

图4 在宇称-时间对称的四能级系统在奇异点处(γ=J),量子态的可区分性的幂律行为.Fig.4.Power-law behavior of the distinguishability of the parity-time-symmetric system at the exceptional point γ=J .
由于线性增益放大器中噪声的量子限制[83],不可能在量子领域中创建具有平衡增益和损失的量子系统[84].奇异点的简并现象也可以在具有模式选择损失的耗散系统中实现.这种被动的宇称-时间对称系统已经在量子领域实现,如单光子[85-88]、超冷原子[36]、超导传输子[89].基于以上基础,针对本文提出的高维希尔伯特空间中的信息恢复与临界性的方案,也可以借助单光子光源去实现耗散系统[90-96],从而观测到宇称-时间对称动力学演化的临界现象.
5 总结和展望
高维的宇称-时间对称系统可以视为两个或者多个最小的非厄米量子系统的组合,为宇称-时间对称性与奇异点简并性的相互作用的量子模型提供了一个新的起点.本文发现流入环境中的信息可以在高维的宇称-时间对称系统中恢复.在非厄米动力学过程中,奇异点扮演着临界点的角色,当系统穿越该点时,信息流动的可逆性变为不可逆,反之亦然.在临界点的周围,量子态间的可区分性这一物理量表现出幂律行为.并且使用量子态的可区分性统一量化了低维与高维宇称-时间对称系统中的信息流动.这些发现可能在量子控制中找到新的应用.
——日晕

