一种基于认知的复杂干扰环境下雷达抗干扰处理方法

王金峰 郝慧军

(1.中国电子科技集团公司第三十八研究所 合肥 230088；2.孔径阵列与空间探测安徽省重点实验室 合肥 230088)

0 引言

随着雷达应用中电磁环境复杂性的不断提高，对雷达抗干扰能力的需求越来越迫切。能否适应复杂的干扰环境成为雷达系统成败的关键。

为了提高雷达在复杂电磁干扰环境中的性能，已经广泛采用了频率捷变、超低副瓣、副瓣匿影、自适应副瓣对消、自适应波束形成、盲源分离等抗干扰措施。自适应副瓣对消和自适应波束形成通过干扰和目标回波在空间响应上的差异，通过干扰协方差统计矩阵在干扰方向形成方向图的零陷，实现干扰的抑制。但当干扰位于主瓣波束宽度内时，目标方向矢量与干扰特征矢量部分相关，造成目标方向的波束无法有效形成，同时引入主瓣方向图的偏移。对于主瓣进入的干扰，学者们提出了基于盲源分离理论的抗干扰方法，其利用干扰和目标回波统计独立的特性，通过对系统响应矩阵的估计，实现目标回波的分离提取。其中基于四阶累积量的特征矩阵近似联合对角化(JADE)算法性能相对稳定，适用于弱目标强干扰环境。盲源方法虽具有较好的抗干扰性能，但其四阶累积量的构建及其排序不确定性会增加系统的复杂度。

本文针对主瓣、副瓣干扰同时存在的环境，提出一种基于干扰环境认知的干扰抑制空域信号处理方法。首先，利用MUSIC算法对线性阵列雷达系统的接收信号进行空间谱估计，得到干扰源的空间分布，并根据雷达波束的指向对主瓣、副瓣干扰情况进行判别；接着构建副瓣干扰子空间，并将阵列信号在子空间投影，实现主瓣保形副瓣干扰抑制；对副瓣干扰抑制后的信号进行多波束合成，形成覆盖主波束的多波束，并通过基于JADE的盲源分离实现目标的提取。该方法对仅有副瓣干扰或者仅有主瓣干扰的环境同样适用。

1 干扰环境的认知

根据抗干扰处理域的不同，抗干扰方法可概括为：频率方法、时域方法、空域方法和极化域方法及多域综合的处理方法。本文方法利用雷达系统的空域信息进行，属于空域抗干扰方法。因此，对干扰环境的认知主要为空间分布信息。

1.1 信号建模

本文以均匀分布的线阵进行讨论，设天线单元数量为，则接收信号矢量表示为

=[,,,…,]

(1)

其由源信号与系统模型共同决定，并将其表示为

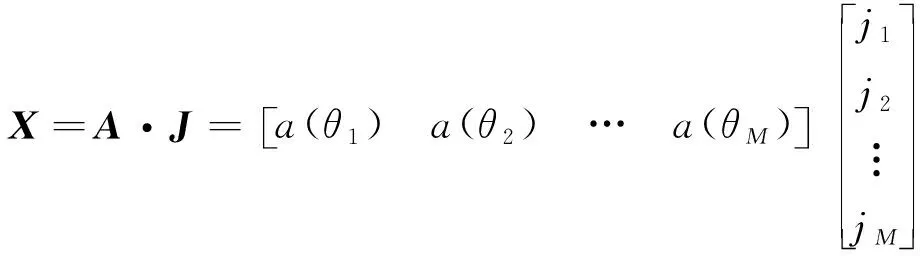
(2)

其中为信号源的数量，并满足<，()=[1,e2πsin,…,e2π(-1)sin]为方向矢量；为单元间距；,=1,…,为源的角度；为波长；,=1,…,表示信号的幅度。

1.2 基于MUSIC的干扰环境认知

基于子空间分解的MUSIC方法已广泛应用于波达方向估计的应用中。在本文中，首先对接收信号进行协方差矩阵估计为

×={}

(3)

其中H表示共轭转置。将其表示为特征值和特征矢量的形式为

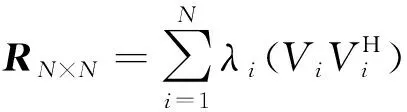
(4)

由于协方差矩阵为正定复Hermite矩阵，其特征值为正实数，对应于信号的能量，对应着个信号源的系统特性。将特征值按照从大到小的顺序进行排列，≥≥…,,…,≥，其对应的特征矢量分别为：,,…,,…,。并定义干扰子空间和噪声子空间为

={,…,}
={+1,…,}

(5)

此时，构建的信号子空间中既包括主瓣干扰，也包括副瓣干扰和可能的目标信号。

那么，MUSIC算法的空间谱由式(6)得到

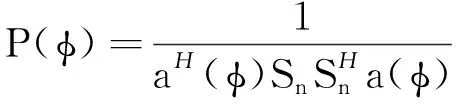
(6)

其中()=[1,ej2πsin,…,ej2π(-1)sin]为方向搜索矢量。通过空间谱估计可以得到所有强信号源的角度分布Φ=[,,…,]，结合发射波束的指向，可判别得到信号源位于主瓣波束还是副瓣波束，及各自的信号源数量：主瓣干扰个，角度为：,…,∈Φ；副瓣干扰个，角度为,…,∈Φ。

2 基于副瓣子空间补的副瓣干扰抑制

由于信号中不仅包含了副瓣干扰，还有主瓣干扰和可能的目标回波，不能直接采用数字波束形成的方式进行副瓣干扰的抑制。本文通过构建副瓣干扰子空间的方式剔除主瓣干扰和目标分量的影响，实现主瓣波束保形的副瓣干扰抑制。

对于副瓣空间角∈Φ,1≤≤可构建其对应的方向矢量()，通过相关性最大的准则找到其对应的子空间特征矢量如式(7)所示。

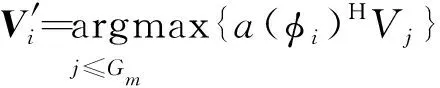
(7)

那么就可以利用副瓣干扰特征矢量构建副瓣干扰空间的补空间如式(8)所示。

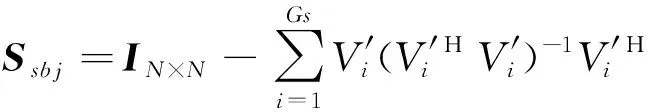
(8)

其中×为维的单位对角矩阵。将阵列信号在子空间的补空间投影，即可得到副瓣干扰抑制的信号。

=

(9)

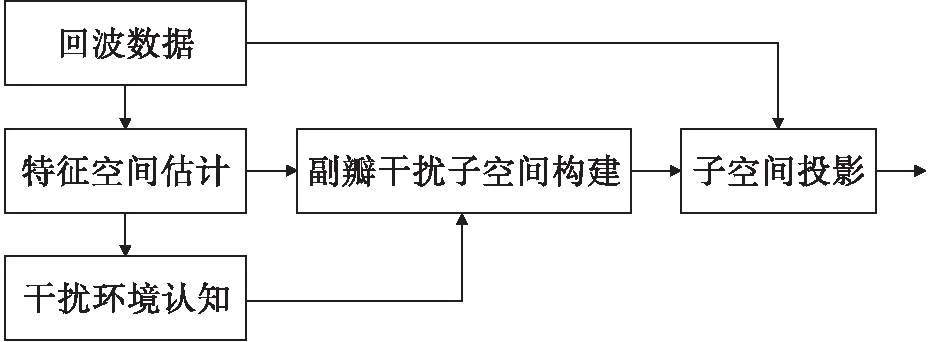
图1 基于副瓣子空间的副瓣干扰抑制

基于副瓣子空间的方法，通过特征向量分解构建副瓣干扰的子空间，可以对包含主瓣目标信号的数据进行处理，对主瓣具有保形的特性。因此该算法不需要干扰信号的采集时序，所有的处理都在当前数据上进行。对干扰变化的场景尤其必要。

3 基于多波束盲源分离的主瓣干扰抑制

盲源分离是从观测到的多源混合信号中分离并恢复出相对独立的源信号的过程。所谓“盲”是指对源信号及混合过程知之甚少，可利用的信息只有观测到的混合信号。干扰环境下的雷达回波不论是源的形式还是系统混合形式均不可知，与盲源分离应用环境相一致。因此，应用盲源分离技术实现雷达主瓣抗干扰的方法越来越得到重视。

3.1 多波束盲源分离

雷达系统中一般采用空间分集实现干扰和目标的分离。然而，雷达系统的单元数一般较大，直接进行盲源处理的运算量大，统计矩阵估计的所需样本数大，难以适应时变的干扰环境。

本文中通过干扰环境的感知，已经得到了主瓣干扰的数量及其对应的角度分布情况。为了充分利用该认知信息，降低运算的维度及复杂度和其它因素(如杂波等)对空间统计特性估计的影响，采用多波束的空间分集形式作为盲源分离的输入。

首先为了获得干扰的高质量统计特性，在主瓣干扰方向∈Φ,1≤≤上构建其对应的方向矢量()，对副瓣干扰抑制后的信号，进行波束合成，得到指向主瓣干扰方向的合成多波束矢量为

=[,…,]

(10)

其中=()·,1≤≤。一般情况下，由于目标信号远小于干扰的强度，很难在干扰环境的认知中得到目标的角度分布。因此，为了尽可能获得指向目标的波束，在主波束角度内再合成个指向均匀分布的波束。

=[,…,]

(11)

其中=()·,1≤≤，为以发射波束中心为原点均匀覆盖波束宽度的指向角度。那么最终得到的波束覆盖分布如图2示意。

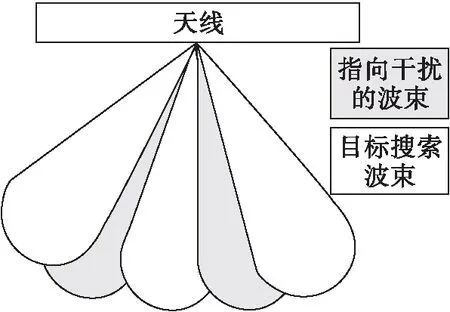
图2 多波束分布示意图

为了后续表示方便，将所有波束域信号表示为矢量形式：

()=[(),(),(),…,()]

(12)

其中，=+；为距离维的快时间。

3.2 基于JADE的盲源分离算法

随着盲源分离技术的不断发展，针对各种应用领域已提出了大量的实现算法。其中，由Cardoso于1993年提出的基于四阶累积量的特征矩阵近似联合对角化(JADE)算法，具有较好的环境适应性，在雷达抗主瓣干扰的应用中得到了一定的应用。

JADE算法利用矩阵迹的酉不变性，简化函数代价函数，将其转化为未知参数构成的列矢量的函数，通过特征值分解得到Givens旋转参数有效估计。其要求混合矩阵为酉矩阵，因此，首先需对空间分集的信号进行预白化处理。

将距离点数为的波束域数据，可将协方差矩阵估计表示为

(0)=[()()]

(13)

对协方差矩阵进行特征分解，将特征值按照从大到小的顺序进行排列，≥…,≥+1…,≥，其对应的特征矢量分别为：,…,,+1,…,。则白化矩阵可构建为

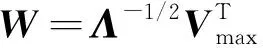
(14)

其中=[,…,,…,]由个大特征值对应的特征矢量构成，并满足>，为对角线矩阵，其对角线元素为-,…,-,…,-，为-个小特征值的均值。

对多波束数据进行白化滤波处理得到

()=W()=[()+()]

=s()+()

(15)

其中，为未知的正交矩阵；为混合矩阵；()为高斯噪声。式(15)表明，只要得到，就可以将源信号()求解出来，从而得到干扰和目标的信号。

JADE算法利用空间维信号的四阶累积量实现与本质相等的酉正交矩阵的估计。定义四阶累积量矩阵()的第行第列表达式为

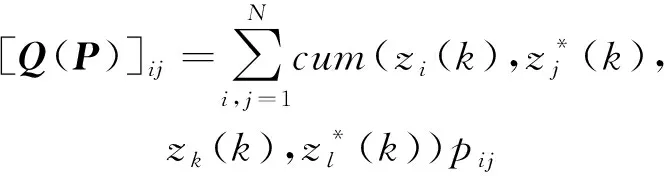
(16)

其中为任意矩阵，为的第行第列元素，(·)为四阶累积量运算。根据累积量的多线性性质，()可表示为多矢量空间投影累加的形式为

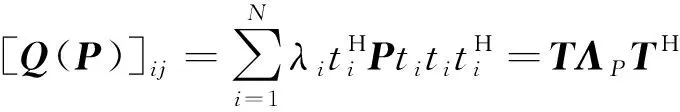
(17)

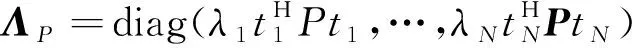
[()]=Σ

由本质相等矩阵带来的排列不定性和相位模糊性并不影响抗干扰的应用。因此，即为混合矩阵的估计，从而通过分离得到源信号的估计为

()=()

(18)

4 仿真验证

本文方法首先通过阵列维度信号利用空间谱估计的方法，获得雷达接收信号的空间分布，实现干扰环境的认知；基于认知信息，构建副瓣干扰子空间的补空间，实现主瓣波束保形的副瓣干扰抑制；基于主瓣干扰的认知信息构建多波束空域分集信号，通过基于JADE算法的盲源分离方法，实现主瓣干扰与目标回波的分离，实现主瓣干扰的抑制。具体实现流程图可总结为图3所示。

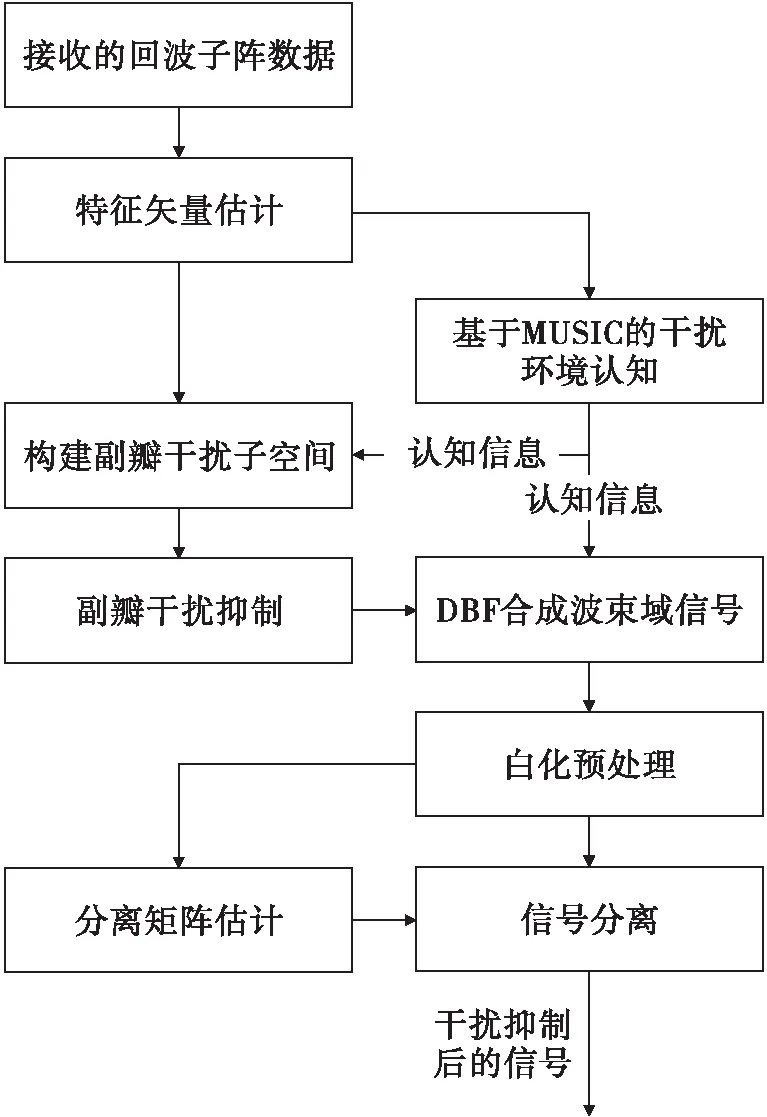
图3 基于认知的抗干扰处理流程

下面采用计算机仿真对本文方法进行有效性验证。回波仿真的线性阵列由32阵元组成，阵元间距为半波长均匀分布，其对应的主瓣波束宽度为3.58°。为了减少脉冲压缩因素对信噪比、信干比的影响因素，仿真采用窄脉冲波形进行(如果是宽脉冲波形则为脉冲压缩后)。波形为0.2μs，对应的等效带宽为5MHz。采样点数为1000点，且目标位于500采样点单元。为了减少波束扫描时波束宽度的影响因素，雷达的工作波束指向法线方向(0°)。目标的幅度设定为0dB，噪声功率为-6dB，对应的波束合成后的信噪比约为21dB。5个干扰分别来自副瓣和主瓣，对应的角度和强度如表1所示。

表1 干扰仿真的环境参数

首先产生各天线单元的接收信号，无干扰和有干扰的回波如图4所示。可见干扰抬高了信号的整体能量水平，此时雷达无法进行有效的目标检测工作。按照本文方法的流程，首先进行干扰环境的认知，对单元回波进行二阶统计矩阵估计后并进行特征分解，得到的特征值分布如图5所示，其中5个大的特征值对应了5个干扰。对其进行MUSIC谱估计，得到空间分布如图6所示。基于雷达主工作波束的指向，可得到环境中包含4个副瓣的(干扰)信号，角度分别为：-30.06°，-10.02°，20.04°和40.08°；1个主瓣的(干扰)信号，角度为：0.5273°。

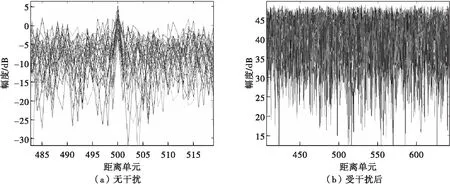
图4 单元级回波信号的幅度分布

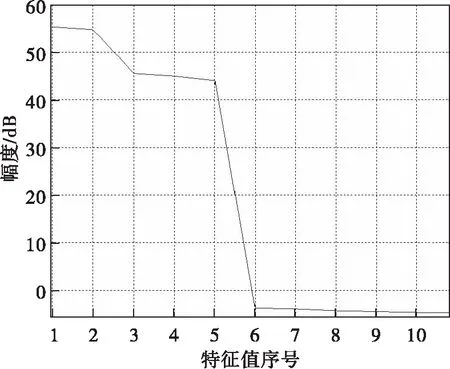
图5 特征值的分布情况

图6 接收信号的空间分布环境

通过特征矢量和干扰环境认知的副瓣干扰角度分布，构建副瓣干扰的子空间补，并投影得到副瓣干扰抑制后信号幅度、特征值分布和空间角分布如图7所示。可见，干扰信号占主要分量，副瓣方向的干扰已经被抑制，只剩下一个空间分量且角度分布在主瓣内。

图7 副瓣干扰抑制后的信号特性

对于仅有主瓣干扰的信号，采用多波束分集进行盲源分离处理。仿真中形成指向主瓣干扰方向0.5273°的波束，再形成5个均匀分布的目标搜索波束(指向分别为-1.8°、-0.9°、0°、0.9°和1.8°，覆盖3.58°的主波束宽度)。对多波束信号进行白化预处理和分离矩阵的估计和滤波，最后通过式(18)实现盲源分离。如图8所示，得到三个分离结果：分离结果1对应最强分量(干扰信号)；分离结果2中得到了分离的目标回波信号，其信噪比为18.1dB，相对波束合成的无干扰情况损失了接近3dB；分离结果3对应比目标更弱的分量(噪声信号)。

图8 主瓣干扰、噪声和目标信号的分离结果

5 结束语

本文针对主瓣、副瓣干扰同时存在的复杂干扰环境，首先通过干扰环境的认知得到主副干扰的情况；再根据副瓣干扰角度构建副瓣干扰子空间补，通过子空间投影实现主瓣保形的副瓣干扰抑制；对于剩余的主瓣干扰，构建多波束空间分集信号，通过基于JADE的盲源分离方法实现主瓣干扰的抑制。仿真处理结果表明该方法具有适应复杂干扰环境的良好性能。