一种LFM 连续波目标多普勒补偿耦合改进算法

叶宇麒

(第七一五研究所，杭州，310023)

近年来连续波探测的相关研究逐渐兴起，其中将传统LFM（Linear Frequency Modulation）脉冲声呐探测消除发射占空比，转变为LFM 连续波探测的方式是相关研究中的热点之一。常规的连续波主动探测信号处理与脉冲声呐探测相似[1]。不同的是连续波探测仅使用LFM 信号，可同时进行多普勒估计与时延估计[2]。此外，连续波处理通过子带信号处理，提高目标更新速率[3-4]，提升目标跟踪性能[5-6]。

连续波探测中，受平台相对运动以及海洋信道传播时变、空变等因素的影响，目标回波发生多普勒频移[7-8]，限制了连续波探测性能。常规的解决方法是对拷贝信号进行多普勒补偿，构建一系列多普勒处理通道，覆盖潜在目标存在的多普勒分布，以提升连续波探测的检测和估计性能。虽然常规处理较为全面的覆盖目标多普勒分布，但随着处理精度的提升，计算存储规模不断增加。因此缩减连续波探测多普勒估计的计算与存储规模，提升疑似目标多普勒观测效率与观测精度，具有极大的应用价值。

本文针对LFM 连续波探测多普勒估计进行了研究，基于常规目标多普勒估计方法提出一种耦合改进方法，利用实验数据验证本文提出的耦合改进方法。

1 问题背景分析

1.1 目标多普勒频移

LFM 连续波信号具有线性时频比例的特点，常见信号短时谱如图1 所示。图中信号带宽B=500 Hz，单周期脉宽T=60 s。传统脉冲声呐探测中LFM 脉冲信号通常被认为是非多普勒敏感信号[4,8]，在连续波探测中，随着处理脉宽的增加，有限带宽的LFM信号的频率分辨能力不断提升[8]。因此，使用LFM连续波信号处理方法可以同时测量回波时延与多普勒。

图1 LFM 连续波信号短时谱

由于目标回波多普勒频偏，匹配滤波器输出增益降低；目标回波峰值受多普勒时延Δτ影响，回波时延τ估计不准确，目标运动模型出现偏差。以不同多普勒假设条件下的子带相关处理为例，仿真目标回波多普勒4.4 m/s，信号参数同图1 信号所示。子带处理带宽BB=50 Hz，子带脉宽TB=6 s，根据信号参数计算LFM 子带宽带多普勒容限βk与多普勒容限速度Vk[9]，其中Vk约为4.4 m/s。分别以0 m/s、4.4 m/s、8.8 m/s 的多普勒速度假设条件对回波做相关，顺序排列子带处理结果，绘制距离时间历程图见图2。

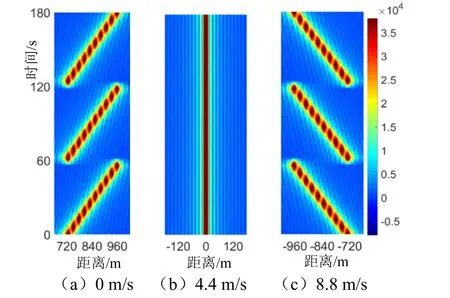
图2 归一化距离时间历程图

图2 中子带中心频率由低到高均匀分布，重复三个周期，距离误差随中心频率递增，最大距离误差为960 m，最小距离误差720 m，当拷贝信号多普勒小于回波时，距离误差为正，大于回波多普勒时，距离误差为负，子带误差分布对称。为减小误差，常规连续波处理通过设置多普勒处理通道，补偿信号多普勒，根据目标最大峰值所需补偿量估计多普勒[10-11]。

1.2 常规处理与计算规模

常规LFM 连续波信号处理中，传感器数据通过降基带、降采样、滤波的基带处理，将数据采样率降低至fs0；基带处理数据通过波束形成处理，将数据输出为Nbeam个波束通道；波束数据通过匹配滤波、能量累计、背景归一化处理输出。输出结果中包括波束通道、子带处理通道、多普勒通道。通常波束通道与子带处理通道是固定的，大带宽B的单周期信号被分解成多个子带BB信号进行处理，以实现探测的连续性，提升目标更新速率，减少不定性区域增长[5]，常规处理流程如图3 所示。

图3 常规LFM 连续波处理流程

多普勒通道数与信号多普勒容限相关，Vk越小多普勒通道数NDoppler越多。在考虑NB个子带处理的条件下，常规连续波多普勒处理每秒数据量为

2 多普勒估计改进算法

为提升多普勒估计精度，减小计算存储规模，本文展开对目标运动模型、多普勒时延补偿的相关研究，并基于常规多普勒补偿方法提出一种耦合改进算法。

2.1 目标运动模型

根据疑似目标距离、方位先验信息，以探测平台为坐标原点，建立直角坐标系运动模型，如图4所示。图中，vs为探测平台航速，vT为目标航速。目标多普勒估计速度v、切向线速度δ分别为

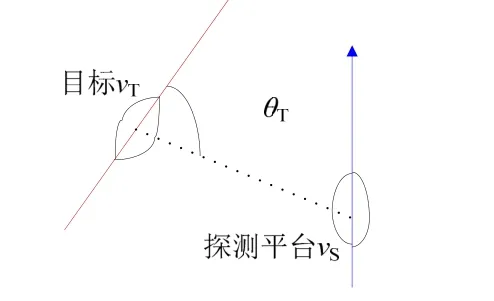
图4 运动模型

多普勒速度v反映了匀速直线模型下一段时间内目标的多普勒估计值，切向角速度ω反映目标相对探测平台舷角变化。

2.2 多普勒时延补偿

相关处理中拷贝信号与回波多普勒速度失配会导致多普勒时延。本文通过模糊函数估计不同多普勒速度下，相关峰值的多普勒时延τ△ ，对目标时延τ进行补偿[12]。LFM 波形的二维相关函数为[9]

因此通过改变拷贝信号多普勒速度可以改变多普勒时延τ△ 。

绘制参数同图1 所示连续波LFM 信号单周期模糊函数，如图5 所示，中心频率1.5 kHz。图中红点位置为多普勒速度2 m/s 假设条件下的相关峰，多普勒时延τ△ ≈0.52 s。将拷贝信号多普勒速度改为0 m/s 假设条件，图中红点将移动至模糊函数原点处。

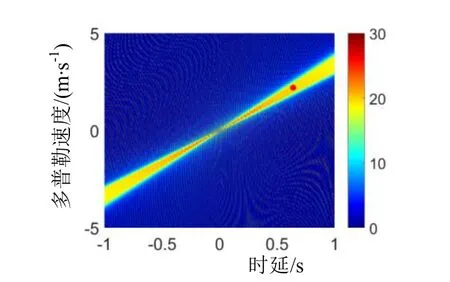
图5 LFM 单周期模糊函数

常规处理通过构建一系列假设多普勒通道，补偿拷贝信号多普勒[13]。在特定的多普勒通道中，拷贝信号与回波信号匹配，获得最大相关峰值，这一通道补偿的多普勒速度μ即为多普勒测量值，测量精度与通道间距V相关。为了获得统一参考系下的回波时延τ，分析频移φ与多普勒时延补偿τ△ 的关系，取模糊函数中峰刃部分[9]，则有

式中，线性调频指数M=B/T。通过多普勒时延τ△ 补偿，修正回波时延τ，减小目标测距误差。

2.3 常规LFM 连续波多普勒估计

常规LFM 连续波信号处理中[14]，多普勒通道设置应全覆盖潜在目标多普勒。其中探测船航速vS与目标估计速度vT是多普勒通道分布宽度主要影响因素。常规处理中，多普勒通道分布宽度|H|∈[vT+vS]，通道固定间距为η。为了维持远离通道分布情况下目标可检测信噪比，根据宽带多普勒容限βk[9]，理论最大通道间距ηmax＜Vk。假设潜在目标多普勒分布为Vmin～Vmax，通道间距为Vk，则最小多普勒通道数为

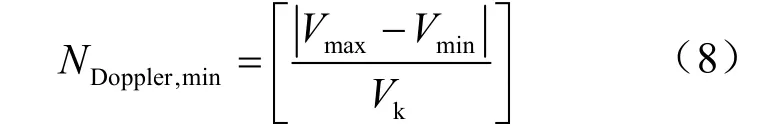
常规连续波处理中，当检测到疑似目标时，首先输出最大目标信噪比所在波束通道beammax，然后选择最大目标信噪比所在多普勒通道。利用提取的疑似目标方位和距离，构建目标运动模型，估计目标多普勒均值。该方法的优点是覆盖多普勒范围广，输出结果较为平稳；不足之处在于高精度的多普勒观测计算量大，输出结果不实时。

2.4 耦合改进算法

本文提出一种耦合改进算法，利用疑似目标先验信息，对目标多普勒进行精细化处理。通过该算法选择部分波束通道与多普勒通道进行计算与观测。将目标运动模型的多普勒估计结果v与多普勒速度测量值μ耦合处理，减小计算存储规模，提升多普勒测量精度与实时性。耦合改进算法分为测量阶段以及目标多普勒跟随阶段、目标波束跟随、耦合处理3 个步骤，利用状态跟随指数ξ评价收敛过程，更新多普勒通道分布宽度与间距。耦合改进处理如图6 所示。

图6 耦合改进处理流程

测量阶段，根据目标发现波束beam0，选取以beam0为中心的N个波束，起始波束beams，终止波束beame，抽取所需目标出现时刻t0所处扫描周期中时长T的数据。选取先验目标多普勒v0为中心的N个多普勒通道。其中起始多普勒通道宽度H0=βkc，多普勒通道边界分别为v1和v2，起始通道间距η0=βkc/(23+1)。在多普勒通道中进行NB个脉宽TB的子带匹配滤波处理，测量目标峰值。提取最大峰值的波束通道，提取多普勒速度测量值vmax，输出目标时延τ。

第1 步 目标多普勒跟随更新跟随状态nζ、多普勒通道宽度H、通道间距η，其中

重复步骤1～3，输出多普勒实时估计结果vD，直至目标跟踪结束。

本文通过耦合改进处理，优化目标观测多普勒通道与波束通道，以减少无效观测，获得更加平稳、精确的多普勒估计结果。

3 仿真分析

多普勒时延估计的精确程度将直接影响多普勒速度的测量值误差与时延补偿后目标距离误差，本文通过多普勒时延仿真，分析理论时延与实际检测误差。通过耦合改进算法仿真，模拟通道收敛过程。

3.1 多普勒时延仿真分析

通过仿真研究不同多普勒速度下目标峰值时延与理论值的误差。以v=2 m/s 的回波信号为例，测量时延Av=2=0.52 s，通过推导可以得到时延理论值

约为0.516 s，同理可得任意多普勒速度条件下的测量时延Av=v1，Av=v2…Av=vn以及理论时延av=v1，av=v2…av=vn。通过仿真与统计多普勒与时延统计结果如表1 所示。

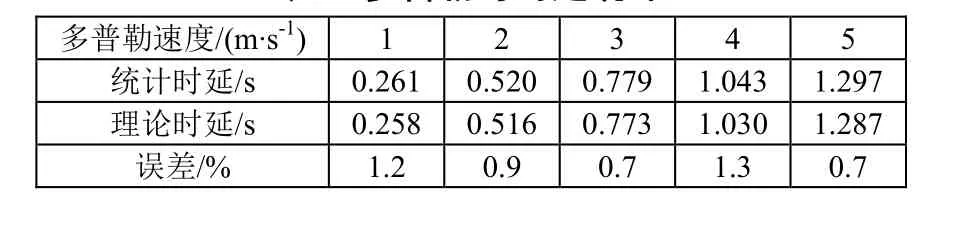
表1 多普勒与时延统计

通过计算，统计值与理论值平均误差为1.0%，最大误差1.3%，最大时延误差0.013 s。时延误差直接反映了拷贝信号理论与实际多普勒补偿的差异。仿真结果证明，多普勒补偿输出值与理论值误差小，可有效减小时延误差。

3.2 耦合算法仿真

耦合算法仿真通过蒙特卡洛实验，模拟收敛系数分别为λ=1～4 条件下的多普勒通道收敛过程，研究收敛速度对通道跟踪结果的影响。仿真中信号参数同图1 信号，仿真时长600 s，进行蒙特卡洛实验10 000 次。仿真中随机速度曲线由正弦函数叠加随机噪声组成。

不同收敛系数结果如图7 所示，以正弦函数曲线为真值测量不同收敛系数条件下误差，随机速度曲线为通道0。λ=1 条件下，通道宽度H与间距η下降速度过快，算法无法收敛。λ=[2,3,4]在图中分别为通道 1～3，蒙特卡洛实验误差均值为E(X)≈[0.06,0.02,0.01]，平 均 误 差 方 差 为D(X)≈[4.5,4.3,3.8]，随着λ增大，收敛速度变慢，误差均值、方差减小，收敛结果更加贴近正弦曲线，受噪声影响更小。

图7 不同收敛系数多普勒通道跟踪结果

进一步提高λ精度的蒙特卡洛仿真实验表明，耦合改进算法在λ＞1.4 时稳定收敛，收敛速度减小，有利于减小误差，λ＞3.7 时误差不再显著变化。为兼顾通道收敛平稳性与收敛速度，实验数据处理中λ=3.6。蒙特卡洛仿真实验表明，算法有效，耦合改进算法重复可行。

4 实验数据处理

本文使用2021 年某水域实验数据，验证耦合改进方法估计疑似目标多普勒速度。目标船与接收端船自航速约2 m/s，多普勒速度分布为-1～7 m/s。目标船于3.5 min 时刻出现，距离7.7 km，探测时长10 min，跟踪时长约6.5 min。探测过程使用信号带宽B=500 Hz，单周期脉宽T=60 s，中心频率f0=1.6 kHz 的LFM 连续波发射。处理过程中子带脉宽TB=6 s。传播损失曲线与声梯如图8 所示。实验区域水文条件良好，水深75 m，声源与接收阵深度45 m。

图8 实验水文条件

4.1 多普勒估计结果

常规处理与耦合改进处理多普勒估计对比如图9 所示，蓝色曲线为常规处理值，红色曲线为耦合改进处理值。处理过程中，子带脉宽6 s，常规处理多普勒通道间距4.4 m/s。以态势规划值为真值，常规处理误差均值为E(X)=1.9 m/s，方差D(X)=3.9，耦合改进算法误差均值E(X′)=0.86 m/s，误差均值降低55%，D(X′)=0.94，误差方差降低76%。耦合处理过程多普勒补偿误差小，受干扰影响小，通道变化连续稳定。

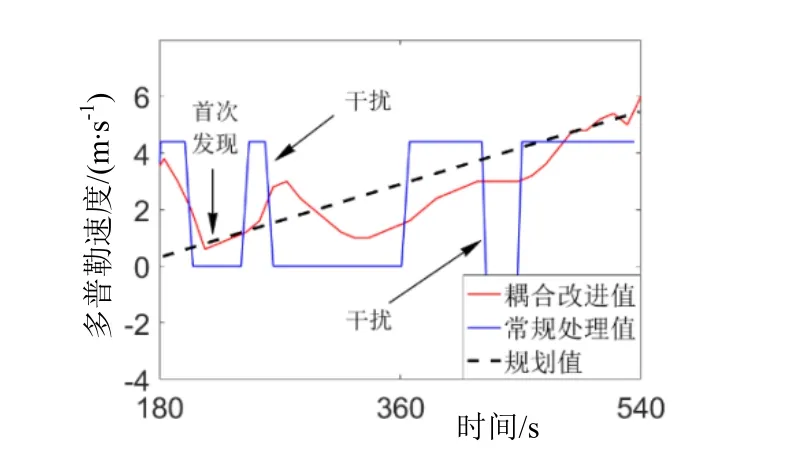
图9 常规处理与耦合改进处理多普勒估计

4.2 目标点迹结果

零多普勒、常规处理、耦合改进处理目标距离时间图与亮点提取如图10 所示。分析目标亮点信噪比，对比图（a）与（c），常规处理提取的亮点簇信噪比高于零多普勒结果。对比图（c）与（e）耦合改进处理后信噪比强度高的回波亮点由分散变为聚集，亮点连续，目标轨迹特征更加明显。

图10 耦合改进方处理前后目标距离时间图

进一步分析回波亮点簇的分布宽度、连续性，提取距离图中亮点与航迹曲线进行比较，如图10（b）、（d）、（f）所示。零多普勒提取结果中，目标点迹具有明显条纹结构，最大连续亮点轨迹约1.9 min；常规处理提取点最大连续亮点轨迹约2.2 min；耦合改进处理后最大连续亮点轨迹2.5 min。耦合改进处理结果相比零多普勒处理结果最大连续航迹时长提升31%，中断时长缩短36 s，目标点迹离散距离区间的均值由0.4 km缩短至0.28 km，缩减30%；相比常规处理最大连续航迹时长提升13.6%，中断时长缩短19 s，目标点迹离散距离区间缩减17%。根据实验结果分析，耦合处理提升了最大连续跟踪时间，使得目标亮点簇分布更加集中，目标航迹与距离变化过程更加清晰。

4.3 计算规模与估计精度

常规估计方法设置固定多普勒总通道宽度H=24 m/s，通道间距ηmax，上限多普勒12 m/s, 下限多普勒-12 m/s，单波束多普勒通道数N=7。常规估计方法单波束批数据处理量Ω=7NBfs0。

耦合处理起始多普勒通道宽度H0=8.8 m/s，起始通道间距ηmax，最大通道间距4.4 m/s，最小通道间距0.49 m/s，单波束通道N′=9；耦合改进方法单波束处理量Ω=5NBfs0。

实验表明，耦合改进处理提升平均多普勒处理测量区间精度51%，最小多普勒通道精度0.4 m/s；减少单波束处理数据量29%，减少计算规模的同时，提升了测量区间精度。

5 结束语

本文针对LFM 连续波常规多普勒估计方法观测区间精度低、计算存储规模大的问题，基于常规方法提出一种耦合改进多普勒估计方法，并通过仿真验证该方法可行性与重复性。实验数据处理表明，LFM 连续波目标多普勒估计耦合改进算法有效降低了多普勒估计误差，相比常规方法，误差均值降低55%，误差方差降低76%；提升了估计结果连续性，目标最大连续航迹时长提升13.7%，目标点迹离散区间缩减17%；提升平均测量区间精度51%，最大多普勒测量区间精度0.4 m/s，单波束处理数据量减少29%。

处理代价降低与精度提升对于无人潜航器等计算能力有限连续波探测平台具有较大应用空间。受实验条件限制，该方法有待通过更多实验数据作进一步验证与改进。