人造米热风干燥特性及干基含水率预测模型

张鹏飞，薛东晓，程 春，张 琦，陈 博，龚俊杰

（1.扬州大学 机械工程学院，江苏扬州 225127；2.江苏丰尚智能科技有限公司，江苏扬州 225012）

0 引言

人造米是一种以淀粉类物料为主要原料，添加其他营养物质、粘合剂等材料混合，通过调质、膨化等工序之后形成外形类似于大米的米制品［1］。人造米水分含量较高，易滋生细菌与发生霉变，不利于运输储存，因此需要后续干燥工艺来降低水分含量。

热风干燥的生产设备结构简单，生产力大，产生的污染与废弃物少，能够满足中小型企业的要求，因此在我国被广泛应用于农副产品加工［2］。热风干燥按照干燥方式可分为一段式干燥和分段式干燥。一段式干燥是干燥条件（温度、风速等）在干燥过程中固定不变的干燥方式；分段式干燥是指在干燥过程中基于物料的特性在不同的干燥时段，采用不同干燥条件的干燥方式［3］。2 种方式在生产中都具有广泛的应用。

在热风干燥过程中，物料含水率是干燥的关键参数之一，为干燥过程的调控和预测提供重要依据。干燥动力学模型可用于预测分析物料在干燥过程中的含水率变化过程，阐明物料含水率变化规律［4］。由于干燥是个复杂的过程，应对不同的物料选出合适的干燥模型。黄枝梅［5］研究得出Modified Henderson and Pabis 模型是描述南瓜片薄层热风干燥的最佳干燥动力学模型；罗燕等［6］研究得出Weibull 模型是描述桔梗热风干燥过程的最佳干燥动力学模型；王昊鹏等［7］研究得出单项式模型是描述籽棉热风干燥的最佳干燥动力学模型；YVAN L.等［8］建立茄子烘焙过程中的传热传质模型和结构力学模型，分析了茄子在烘焙过程中的水分损失和体积收缩的变化规律。已有大量的文章和研究对干燥的物料进行干燥动力学模型研究与干燥特性分析［9-10］，但人造米是新物料，研究较少，尚未建立相关合适的模型。

本文以人造米为研究对象，采用热风干燥技术，探究风速、温度和料厚对干燥过程的影响并计算其有效水分扩散系数（Deあ）；建立基于指数函数的新型干燥动力学模型，对干燥过程中含水率变化规律进行模拟与预测。旨在为人造米热风干燥参数优化提供理论依据。

1 试验设备材料及方法

1.1 试验平台及材料

干燥平台：自制，其设备与结构风路如图1所示；MA45 型快速水分测量仪（精度±0.001 g，德国赛多利斯公司）；人造米，由天津某公司提供，大小均匀，无裂纹、蛀虫及霉变等损坏现象。

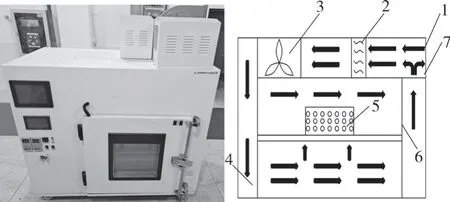
图1 试验装置与原理风路图Fig.1 Experimental device and schematic diagram of wind circuit

1.2 试验设计

设计温度变化试验、风速变化试验和料厚变化试验，具体参数如表1。试验具体操作：首先运行烘干机试验装置，开启换热器与循环风机，根据试验要求设定循环风速与烘干温度；然后等烘干机运行到设定温度后，将物料平铺在225×355×150 mm 的载物框中，框底部均布有圆心距为22.5 mm 的φ7 mm 圆形小孔，框底部铺有40 目筛网；最后将载物托盘放入烘干室内，设定试验时间为40 min，每隔8 min 取出少量物料放入塑料密封袋中保存并将料层铺平，使用快速水分仪测量物料含水率。

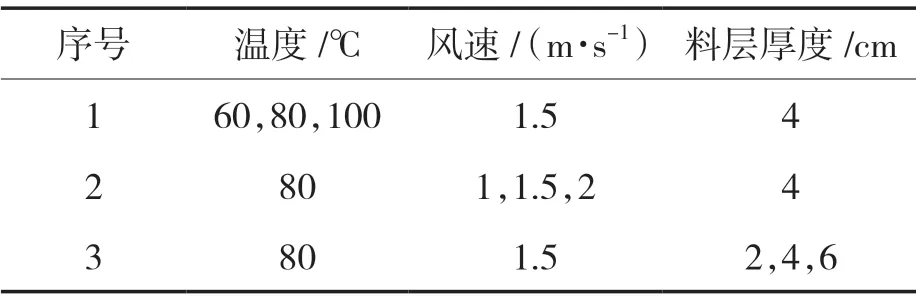
表1 试验条件参数Tab.1 Experimental condition parameters

1.3 含水率测定

参照GB5009.3-2016《食品中水分含量的测定》，采用直接干燥法测定人造米含水率，计算方法如下式所示：

式中 w——物料含水率，%；

m——物料的质量，g；

me——干燥后物料的质量，g。

1.3.1 干基含水率的测量

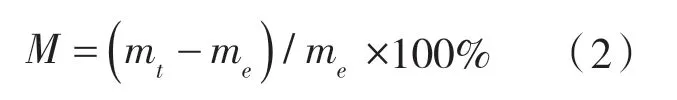
式中 M——t 时刻物料的干基含水率，%；

mt——t 时刻物料的质量，g。

1.3.2 干燥速率计算

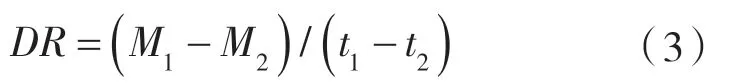
式中 DR——干燥速率，g·（g·min）-1；

M1——t1时刻物料的干基含水率，%；

M2——t2时刻物料的干基含水率，%；

t1，t2——干燥时间，min。

1.3.3 有效水分扩散系数

在干燥过程中，物料的水分扩散包括毛细管流动、水动力流动和分子扩散等，是一个复杂的过程，一般用有效水分扩散系数来表示水分在物料中扩散传递速率的大小，是一个动态量。假设物料中水分传递以扩散为主，初始水分分布均匀且水分扩散系数在干燥过程中恒定，不考虑收缩的情况下，可以使用简化的Fick 第二定律计算得到：

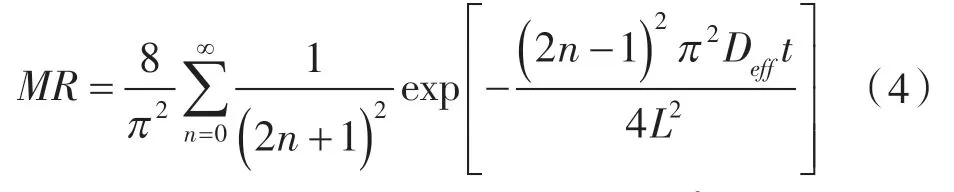
式中 Deあ——有效水分扩散系数，m2/s；

L——料厚的一半，m；

n——试验组数；

t——干燥时间，s。

当烘干时间较长时，可简化：

对式（5）两边同取自然对数：

lnMR 与干燥时间t 呈线性关系，可由直线斜率求出Deあ。

2 试验结果分析

2.1 人造米的热风干燥特性

由图2（a）所示，固定料层厚度为4 cm，风速为1.5 m/s，干燥温度分别为60，80，100 ℃，随着干燥的进行，人造米的M 由最初的25.05%，到干燥结束时分别下降到7.79%，6.37%，5.09%；且随着温度增大，人造米的最终M 逐渐降低。由图2（b）可知，人造米热风干燥主要为降速干燥阶段，存在明显的升速干燥期。在8 min 干燥速率分别达到最大值1.03，1.343，1.645 g·g-1·min-1，而后进入降速干燥段，在干燥结束时分别降至0.131，0.07，0.054 g·g-1·min-1。

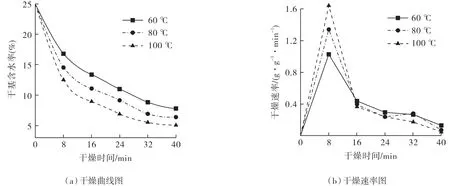
图2 人造米不同温度下干燥特性曲线Fig.2 Drying characteristic curves of artificial rice at different temperatures

由图3（a）所示，固定料层厚度为4 cm，干燥温度为80 ℃，风速分别为1，1.5，2 m/s，随着干燥的进行，人造米M 分别由最初的25.05%下降到干燥结束时的7.82%，6.37%，5.66%；且随着风速的增大，人造米的最终M 逐渐降低。由图3（b）所示，人造米在前期有明显的升速干燥期。在8 min 时分别达到最大值0.835，1.13，1.325 g·g-1·min-1，而后进入降速干燥阶段，在干燥结束时分别降至0.086，0.108，0.889 g·g-1·min-1。这可能是因为干燥前期，人造米水分含量高，干燥外部条件占据主要地位。风速越高，人造米的流动边界层越薄，增大了人造米表面与空气的热交换，前期干燥速率越快。

图3 人造米不同风速下干燥特性曲线Fig.3 Drying characteristic curves of artificial rice at different wind speeds

由图4（a）所示，固定风速为1.5 m/s，干燥温度为80 ℃，料层厚度分别为2，4，6 cm，随着干燥的进行，人造米的M 由最初的24.29%分别下降至干燥结束时的5.3%，6.12%，8.13%；随料层厚度的增加，人造米最终M 逐渐提高。且在试验中发现料层越厚，人造米在干燥过程中堆积层数越多，干燥介质由下而上穿过人造米过程中，温度逐渐降低，湿度逐渐升高，干燥驱动力逐渐减小，人造米的底层含水率低于高层含水率，人造米干燥均匀性变差。由图4（b）所示，人造米在前期有明显的升速干燥期。在8 min 时分别达到最大值1.551，1.231，0.936 g·g-1·min-1，而后进入降速干燥阶段，在干燥结束时分别降至0.103，0.095，0.2 g·g-1·min-1。随着料厚的增加，人造米的前期干燥速率逐渐减小，且随着料层的增加，在干燥后期出现一段近似匀速干燥期。这可能是由于随着料层变厚，干燥均匀性变差，在干燥中期，底层人造米在快速干燥期，穿过上层人造米时干燥介质温度降低，湿度提高，上层人造米的干燥速率降低；在底层人造米含水率下降后，底层人造米干燥速率下降，干燥介质在穿过上层人造米时温度提高，湿度降低，上层人造米的干燥速率提高，在干燥中后期呈现出一段近似的匀速干燥期。

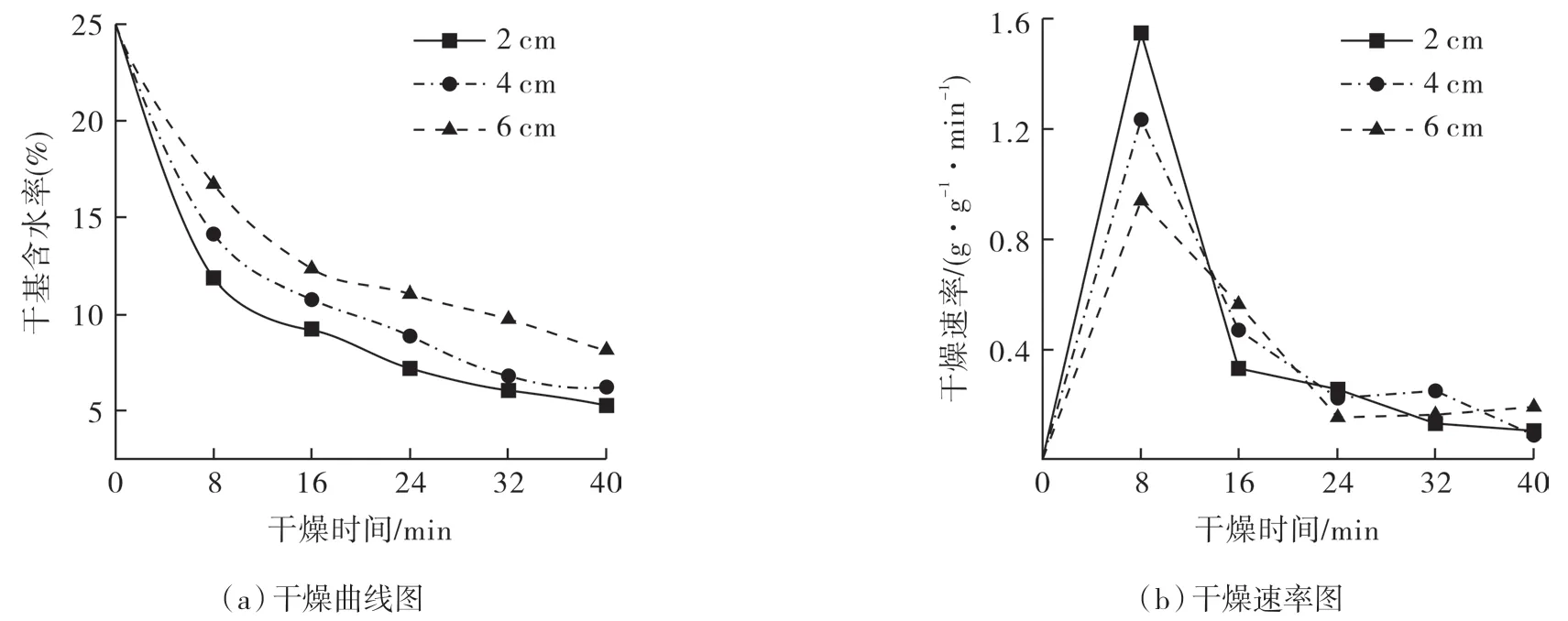
图4 人造米不同料层厚度下干燥特性曲线Fig.4 Drying characteristic curve of artificial rice under different thickness of feed layer

由图2（b），3（b），4（b）所示，不论烘干条件如何改变，人造米含水率始终在烘干初始阶段下降较快，而后含水率下降逐渐减慢。这是因为在烘干初期人造米通过内部水分向表面的转移与表面水分的汽化而干燥。在烘干初期，人造米表面含水率高，干燥速度快，含水率变化就大。随着干燥的进行，人造米的汽化面逐渐向内部转移，内部的扩散阻力较大，干燥速率下降，含水率变化变小。

2.2 人造米有效水分扩散系数

不同干燥条件下有效水分扩散系数由表2所示。热风温度从60 ℃增至80 ℃，风速从1 m/s 增至2 m/s，料层厚度从2 cm 增至6 cm，相应的Deあ分别增加了1.424，1.177，8.395 倍。由此可得，对于人造米Deあ的影响排序：料层厚度>干燥温度>风速。

表2 不同干燥条件下人造米有效水分扩散系数Tab.2 Effective water diffusion coefficient of artificial rice under different drying conditions

3 干燥模型的建立与验证

3.1 干燥模型的建立

在烘干过程中，物料失水是一个复杂的传质传热过程。烘干机内部温度越高，风速越大，物料失水的速度也相应越高。由于料层厚度在烘干过程中影响相对湿度、风速等诸多因素，无法准确地确定其变化原因，因而只针对干燥温度与干燥风速，建立干燥动力学模型，用于预测烘干过程中物料含水率的变化：

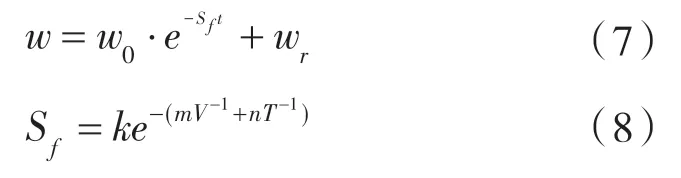
式中 w——物料的实时含水率，g/g；

T——温度，℃；

w0——初始含水率，g/g；

wr——不可干燥含水率，g/g；

V——风速，m/s；

k、m、n—— 模型参数，其中，n 反应温度对物料失水率的影响效果，m 反应风速对物料失水率的影响效果。

3.2 干燥模型的参数求解

通常物料的初始含水率不为w0，而为当下含水率ws，因此模型干燥时间为实际干燥时间与假想干燥时间ts的和。由式（7）得：

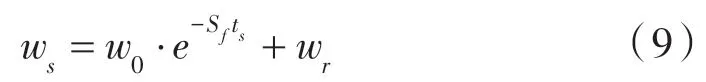
化解得：

以试验数据为基础，采用最小二乘法，使模拟数据无限逼近试验数据，从而确定模型参数。最小二乘法表达式如下：

式中 d（k）——试验模拟数据；

此方法原理在于对于每个参数在给定范围内，都能找到一个参数值，求得f（k）最小值，使模拟数据无限逼近于试验数据。数学模型参数所求值如表3所示。

表3 数学模型参数值Tab.3 Parameter values of mathematical model

3.3 干燥模型评价

对于此类数据拟合模型，通常使用模型相关系数（R2）与均方根误差（RSEM）来评价模型拟合程度的好坏，R2值越接近于1，RSEM 越小，则模型拟合程度越好。由表4可得R2均大于0.983，RSEM 均小于0.007，表明模型拟合度程度好，能够准确预测人造米在干燥过程中含水率的变化情况。

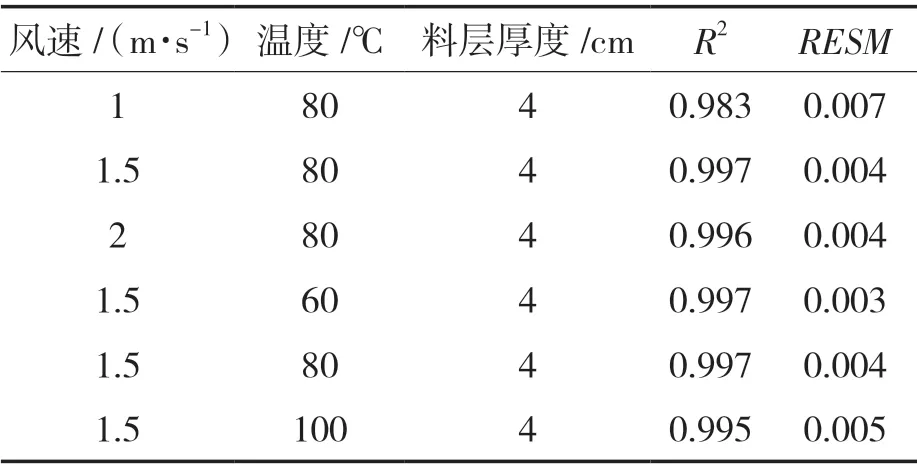
表4 不同干燥条件下模型决定系数Tab.4 Model determination coefficient under different drying conditions

4 结语

（1）不同风速、干燥温度、料厚条件，人造米开始为升速干燥阶段，而后进入降速干燥阶段，无明显匀速干燥期。

（2）以干燥温度、风速、料厚为变量，进行多组人造米干燥试验，对试验数据进行拟合，得出3个变量对人造米有效水分扩散系数影响关系：料层厚度>干燥温度>风速。

（3）为预测人造米干燥过程水分变化规律，建立一种人造米干燥动力学模型。以热风温度与风速为变量，进行多组试验，对试验数据进行拟合，发现模型决定系数均大于0.983，均方根误差均小于0.007，模型拟合度较好，能够准确预测干燥过程中人造米的水分变化。