类矩形盾构隧道下穿引起既有隧道竖向位移计算方法研究
魏 纲, 赵得乾麟, 齐永洁
(1. 浙大城市学院土木工程系, 浙江 杭州 310015; 2. 浙江省城市盾构隧道安全建造与智能养护重点实验室, 浙江 杭州 310015; 3. 城市基础设施智能化浙江省工程研究中心, 浙江 杭州 310015;4. 广州南沙资产经营集团有限公司, 广东 广州 511466; 5. 浙江大学建筑工程学院, 浙江 杭州 310058)
0 引言
近年来随着城市的高速发展,城市地铁线路越来越密集,新建隧道周边难免存在已建隧道。类矩形盾构隧道具有空间大、稳定性高的优点,成为城市隧道建设的新选择。新建类矩形盾构隧道从既有隧道周边穿越会对既有隧道结构造成影响,甚至破坏既有隧道稳定性,造成严重的安全事故。因此,针对类矩形盾构隧道施工对邻近既有隧道造成的影响开展研究具有重要意义。
针对现有盾构隧道施工对既有隧道造成影响的研究方法,可分为以下几类。1) 理论分析法[1-4]。例如: 魏纲等[1]基于Mindlin位移解和随机介质理论,考虑多因素的影响,提出了类矩形盾构隧道施工引起土体竖向位移计算公式;张治国等[2]基于镜像法和Winkler 地基模型,提出了类矩形盾构隧道施工造成邻近既有管线变形计算方法。2) 现场实测法[5-6]。例如: 司金标等[5]对宁波轨道交通3号线地表变形、土体分层沉降进行了现场实测;王东方等[6]对管片受力变形进行了现场实测。3) 数值模拟法[7-9]。例如: 季昌等[7]通过对类矩形盾构隧道施工进行模拟,研究了土体与盾壳摩擦作用下周边土体的变形情况。4) 模型试验法[10-12]。例如: 魏纲等[10-11]依托宁波轨道交通3号线开展缩尺比为1∶20的室内模型试验,研究了类矩形盾构施工对邻近管线造成的影响;张治国等[12]采用排液法模拟类矩形盾构隧道施工,研究了隧道施工对邻近管线造成的影响。目前的研究对象主要为圆形盾构隧道,针对类矩形盾构隧道的研究较少,且主要围绕隧道对土体以及周边管线和建筑物的影响,对周边既有隧道造成影响的研究尚未发现。因此,有必要开展类矩形盾构隧道施工对邻近既有隧道造成影响的研究。
本文基于随机介质理论并结合累积概率曲线,将圆形隧道计算方法拓展到计算类矩形盾构隧道施工由于土体损失造成的土体竖向位移中,再通过转动错台协同变形模型计算既有隧道竖向位移。随后,针对类矩形盾构隧道下穿既有隧道开展室内缩尺模型试验,对既有隧道拱顶位移进行测量。最后,将本文方法与模型试验测量结果进行对比,验证本文方法的可靠性。
1 研究现状
1.1 随机介质理论
Litwiniszyn[13]基于砂箱模型试验研究,建立了随机介质理论。该理论将土体视为“随机介质”,认为开挖造成土体下沉是一种随机的过程,并从统计的观点,把隧道开挖造成土体沉降看作无数个小开挖对土体造成的沉降总和。阳军生等[14]将该理论拓展到预测隧道施工引起的地表位移计算,但没有考虑盾构施工中多种复杂因素对土体造成的影响。魏纲等[15]对该理论进行了修正,得到双线平行盾构施工地表沉降计算方法; 随后,在此基础上进行了公式拓展,提出了考虑多因素的类矩形盾构隧道施工地表沉降计算方法[1],效果良好。
1.2 累积概率曲线
Attewell等[16]采用累积概率曲线公式计算土体损失引起的隧道轴线上方纵向地面沉降,
(1)
式中:S(x)为沿隧道掘进方向坐标x处的纵向地面沉降量;Smax为最大沉降量;x为地面计算点沿隧道掘进方向的坐标;xi为隧道开挖面推进起始点;xf为当前隧道开挖面的位置;i为地面沉降槽宽度系数,i=kH(k为沉降槽宽度参数,H为开挖隧道埋深,详细介绍参考文献[17]);Φ函数可由标准正态分布函数表查得。
魏纲等[18]将累积概率曲线的方法运用到顶管施工土体沉降计算中,效果良好。
1.3 转动错台协同变形模型
魏新江等[19]采用Boussinesq 解计算地面堆载对临近地铁盾构隧道的附加应力,建立了综合考虑剪切错台变形和刚体转动变形的隧道变形计算模型,采用最小势能法建立了隧道变形的变分控制方程,推导出隧道的纵向变形量、环间剪切力、错台量和环间转角的计算公式。
魏纲等[20]将转动错台协同变形模型,用于基坑开挖引起邻近旁侧盾构隧道的转动与错台变形计算。随后,考虑施工因素的附加荷载作用下,运用转动错台协同变形模型,对既有盾构隧道在新建隧道穿越时的结构变形进行了分析预测[21]。
但目前上述方法未运用在类矩形盾构隧道穿越既有隧道的研究中,可行性有待验证。
2 本文计算方法
2.1 计算模型及假设
本文主要研究类矩形盾构隧道施工中土体损失引起的土体及既有隧道竖向位移。假设土体为均质的线弹性半无限体,盾构在施工过程中不发生偏移。本文计算分为2个阶段,先基于随机介质理论并结合累积概率曲线计算类矩形盾构开挖土体损失造成的土体竖向位移,再通过转动错台协同变形模型计算圆形既有隧道的竖向位移。
本文计算模型见图1和图2。从图2可知,类矩形盾构隧道截面可近似看成2个半圆与1个矩形组合而成,因此,截面面积A=πR12+4R1d(R1为圆形半径,2d为矩形边长)。
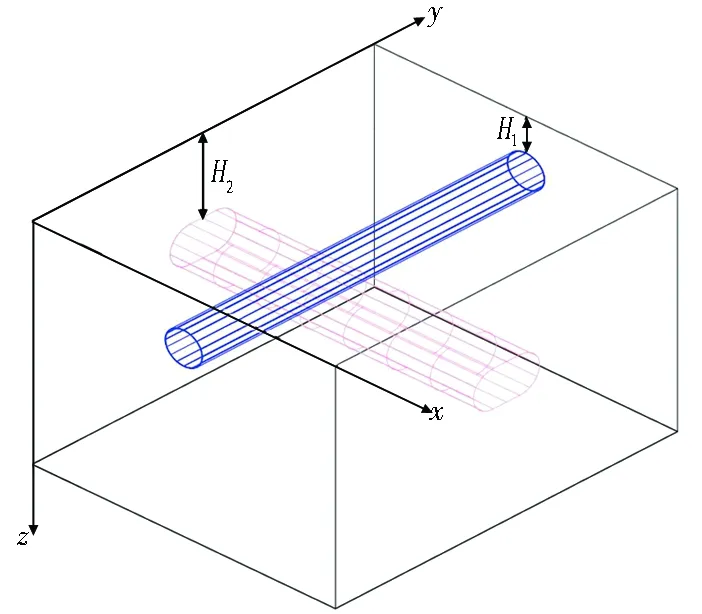
H1、H2分别为上线、下线隧道顶部覆土埋深; x轴为新建隧道开挖方向; 蓝色为既有隧道,红色为新建隧道。

图2 类矩形盾构隧道断面图
2.2 土体损失引起的土体竖向位移计算
魏纲等[1]基于随机介质理论推导出类矩形盾构隧道施工由于土体损失造成的土体竖向位移计算公式。地面以下点(ξ,η)处无限小微元开挖,当开挖单元完全塌落时引起(y,z)坐标处土体沉降,
(2)
其中,
(3)
式中h1为隧道开挖面轴线埋深。
断面上土体损失引起的土体沉降
(4)
式中:E为类矩形盾构隧道施工开挖区域;C为开挖面收敛后的形状区域;开挖面区域形心坐标为(0,h1),开挖面收敛后区域形心坐标为(0,h2)。
若要得到三维土体沉降公式,需要在既定工况下得到沿隧道掘进方向(x方向)的每一个横断面的土体损失率ε(x),进而计算出每一个横断面的土体沉降,再将其组合,土体沉降就可以沿纵向得以延拓。
结合文献[22],由Peck公式可知,既有隧道最大土体损失率εmax与隧道轴线上方的地面最大沉降量Smax成正比,即满足:
(5)
即
(6)
将式(6)代入式(1)可得:
(7)
根据文献[1]可知,等效土体损失参数g与土体损失率ε的关系式为:
(8)
通过式(7)和式(8)可得到:
(9)
将g(x)代替式(4)中所有用到的等效土体损失参数g,则土体沉降公式沿纵向得以延拓,得到三维土体沉降计算公式:
(10)
2.3 既有隧道竖向位移计算
根据隧道位移的2阶段求解方法,第1步求得隧道沿纵向所受的附加应力值,第2步利用相应隧道模型求解隧道产生的位移值。
在2.2节的基础上,可求得土中一点(x,y,z)所受的竖向附加应力值
σz=Kw(x,y,z)。
(11)
式中K为土的基床系数。
将求解点(x,y,z)布置在既有隧道轴线上,即可求得既有隧道沿轴线所受的附加应力分布。
在第2步计算中,本文通过文献[21]中提出的剪切错台和刚体转动协同变形模型对既有隧道的竖向位移进行计算。该模型基于能量变分法,由周顺华等[23]提出的剪切错台模型进一步发展而来,认为隧道的纵向变形形式包括管片环转动和错台变形。该模型已在文献[19-21]中进行了详细的介绍,本文不再对公式推导过程进行赘述。
既有隧道的竖向位移w最终计算公式为:
w={Tn(l)}AT。
(12)

3 可靠性验证
3.1 试验介绍
本文以宁波轨道交通3号线1期出入段为工程背景,采用1∶20相似比进行缩尺模型试验,模拟了新建类矩形盾构隧道90°下穿圆形既有隧道工况,如图3和图4所示。
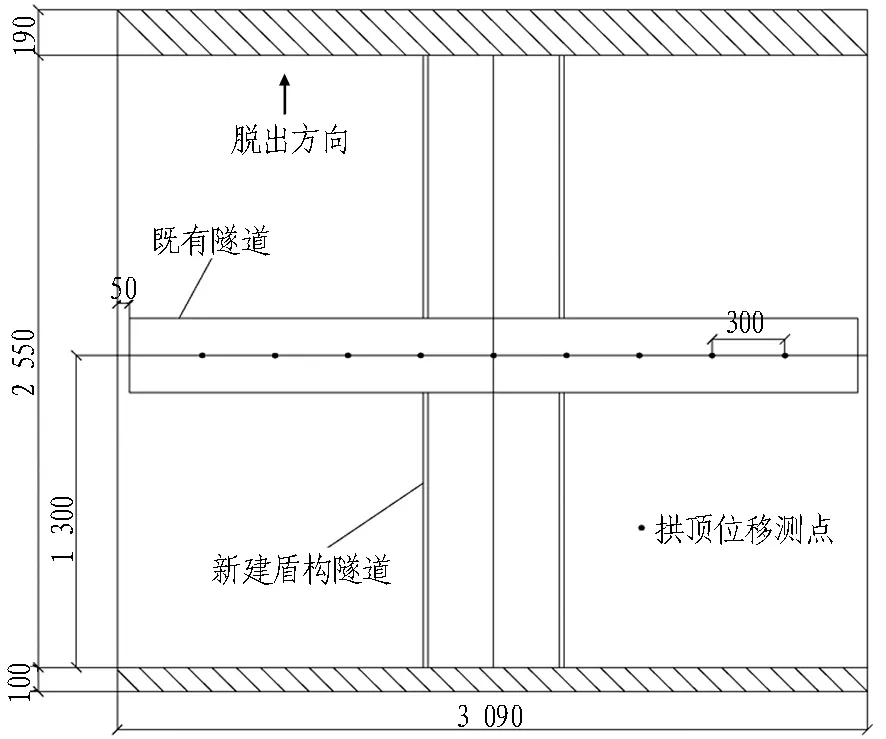
(a) 俯视图

(b) 正视图
模型箱尺寸为3 m×2.5 m×2.1 m(长×宽×高),既有隧道埋深H1为310 mm,新建类矩形盾构隧道埋深H2为720 mm,隧道间距100 mm;土体损失率为5%,采用干砂模拟,干砂压缩模量为6.28 MPa。为确保新建隧道不会因为自身变形导致既有隧道及周边土体受到影响,类矩形盾构选用2.5 mm厚的钢结构制作而成;既有隧道则根据实际隧道的结构物理参数,以1∶20的缩尺比进行选材,选用聚乙烯PE圆管。二者之间选材不同的原因,一方面是确保新建隧道不对试验结果产生额外影响,另一方面是让既有隧道尽可能还原实际工程中的隧道。本试验在既有隧道拱顶设置9个位移测点,以隧道中心对称布置,每300 mm布置1个。试验相关参数见表1。
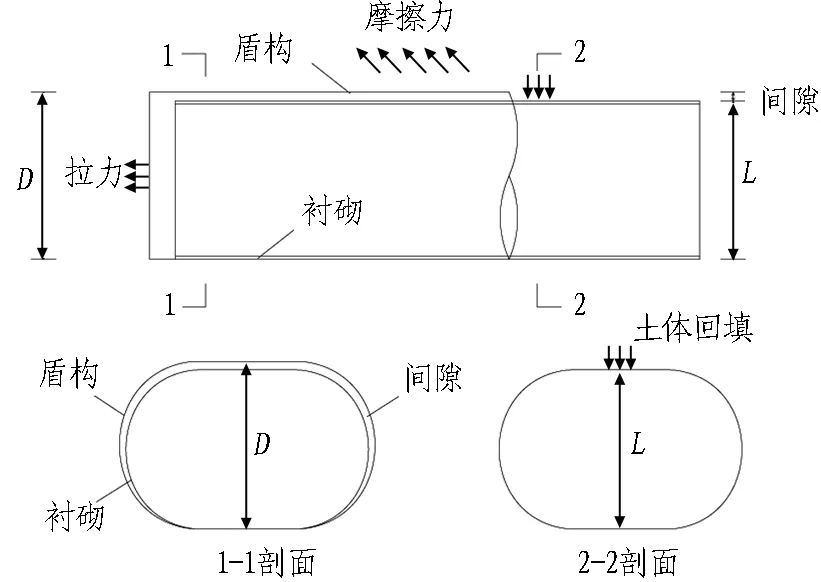
D为外筒竖向直径,长度为35 cm; L为内筒竖向直径,长度为34 cm。

(b) 模型箱实物图

表1 试验相关参数
本试验采用外筒套内筒并抽出外筒的方法模拟土体损失。外筒代表盾构,内筒代表隧道衬砌,内外筒之间的间隙即为盾构开挖造成的土体损失。由于外筒抽出过程中与土体存在摩擦力,因此,试验结果受到一定的影响。
试验步骤为: 1)将内筒嵌套入外筒中模拟盾构,推入嵌套好的盾构模型到模型箱内并固定住内筒; 2)密封好空隙后均匀地覆砂至既有隧道设计埋深处,并安放既有隧道; 3)检测既有隧道上的测量设备运作情况后,继续覆砂至设计高度,期间每10 cm夯实1次砂土; 4)静置24 h后进行试验前测量设备检查工作; 5)利用卷扬机抽出外筒模拟盾构开挖,同时记录外筒抽出过程中的全部试验数据。
3.2 理论计算与结果分析
参考文献[17],砂土k值取0.2。将本文试验结果放大20倍进行计算以模拟实际工程情况。由于试验中新建隧道未通过既有隧道轴线时,外筒与土体存在摩擦力会影响计算结果,因此,分别计算新建隧道通过既有隧道0.6、0.9、1.2 m(实际工程为12、18、24 m)时对应的拱顶位移并与实测值进行比较,见图5—7。不同阶段拱顶位移实测值见图8。
对比图5—8可发现,既有隧道拱顶沉降随着开挖面的离开逐渐增大。同时,随着开挖面离开,本文计算结果与实测结果的贴合程度越来越高,究其原因是随着开挖面的离开,拱顶沉降逐渐稳定,实测数据不受其他因素影响,因此理论值与实测值逐渐吻合,说明本文计算土体损失引起隧道拱顶沉降的方法可行。

图5 x=12 m时拱顶位移对比

图6 x=18 m时拱顶位移对比

图7 x=24 m时拱顶位移对比
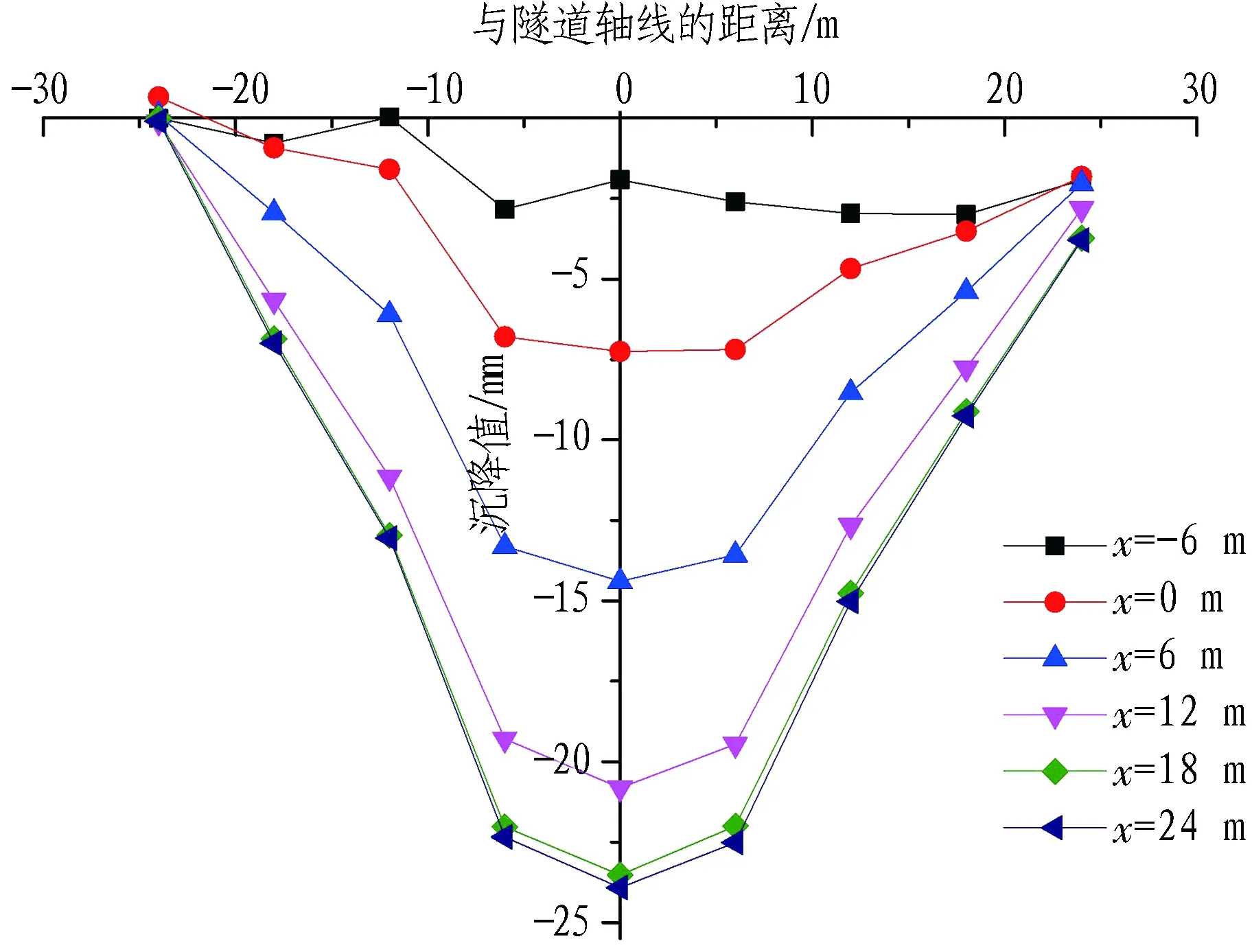
图8 不同阶段拱顶位移实测值
4 影响因素分析
下文基于本文方法开展既有隧道拱顶变形的影响因素分析。通过理论计算,分析新旧隧道间距为0.6D(D为隧道外直径)、正交下穿既有隧道时,随着隧道开挖面的掘进,既有隧道拱顶产生的位移变化如图9所示。
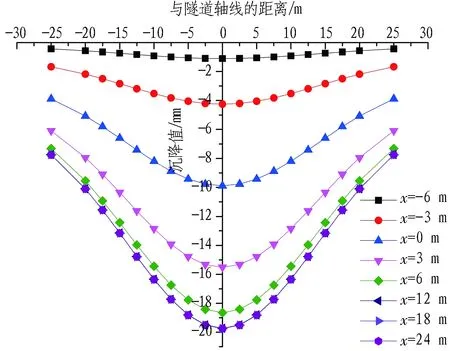
图9 不同阶段拱顶位移理论计算结果
从图9可知,新建隧道未开挖到既有隧道轴线时,既有隧道拱顶已开始发生变形,随着隧道开挖面向前掘进,既有隧道拱顶变形逐渐增大,并且在既有隧道轴线附近的变形增长幅度最大;当开挖面离开一段距离后(x=12 m)拱顶变形基本稳定。因此,新建隧道穿越既有隧道时由于土体损失的影响会存在一段快速变形的过程,该阶段对既有隧道的结构安全会造成一定的威胁,后续可针对该阶段进行深入研究和分析。通过对比图8和图9可以发现,实测数据与本文计算结果规律一致,进一步证明了本文方法的可靠性。
与前文隧道间距0.6D的理论计算结果进行对比,分析隧道间距不同时既有隧道拱顶变形情况,结果见图10。由图可知,随着隧道间距的增大,既有隧道拱顶变形减小,表明隧道间距与既有隧道拱顶变形大小成反比;隧道间距不同时,既有隧道拱顶变形整体趋势基本一致;靠近新旧隧道相交位置的拱顶变形存在一定差别,表明正交工况下隧道间距的不同对新旧隧道交汇处的拱顶变形影响较大。
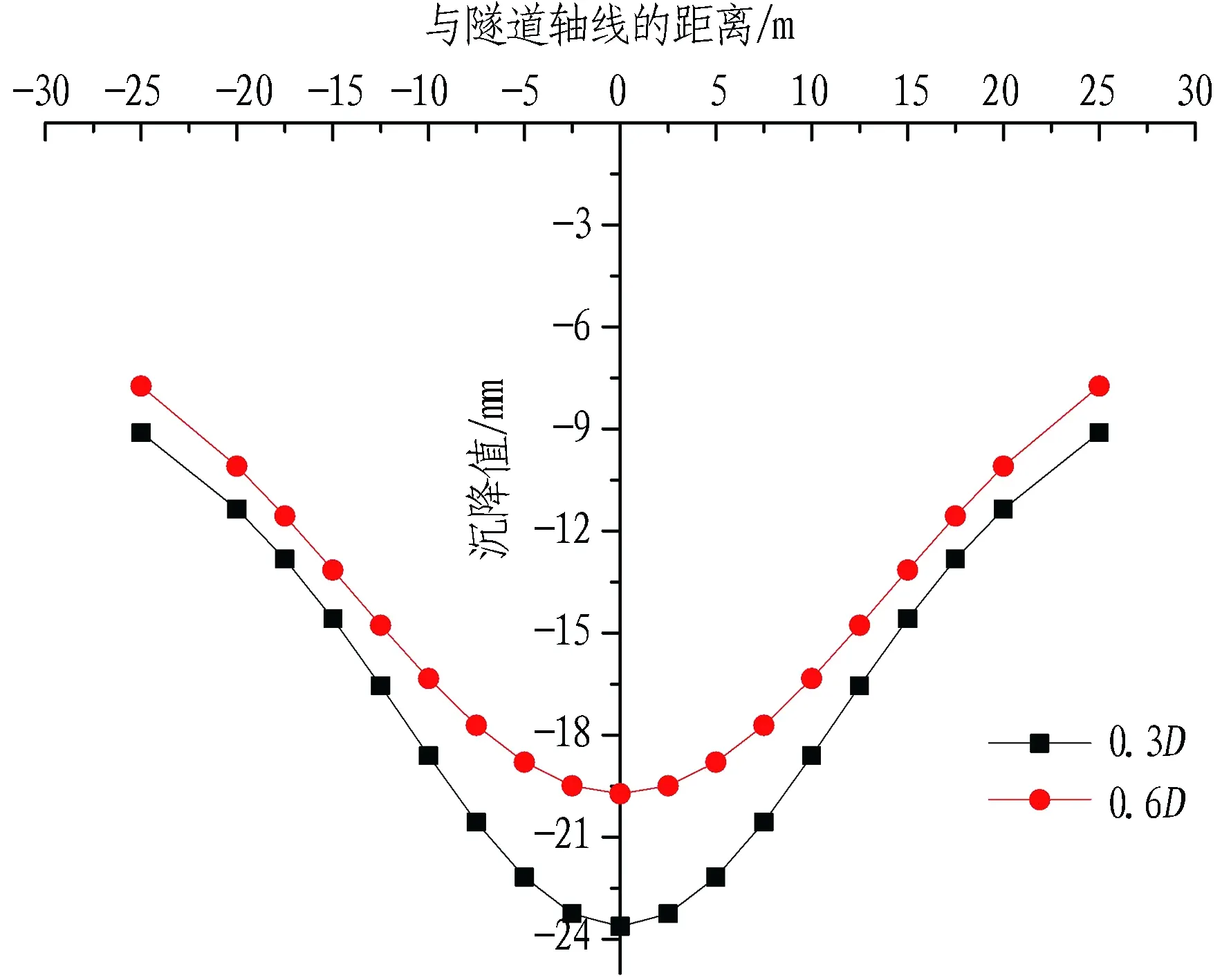
图10 x=12 m时不同隧道间距对应的拱顶位移
5 结论与讨论
1)本文基于随机介质理论并结合累积概率曲线计算土体损失造成的土体竖向位移,再通过转动错台协同变形模型计算既有隧道竖向位移。将本文计算结果与室内模型试验测量结果进行对比,证明本文方法可行。
2)针对类矩形盾构隧道施工对邻近既有隧道造成的影响开展室内模型试验,研究了随着新建类矩形盾构隧道开挖,上方既有隧道拱顶在土体损失作用下发生的竖向变形情况。研究表明: 不同隧道间距穿越既有隧道时,既有隧道拱顶变形规律基本一致,新旧隧道交汇处的拱顶变形受影响较大。
3)随着新建类矩形盾构隧道的开挖,上方既有隧道的拱顶变形逐渐增大,并存在一个快速变形的阶段,当开挖面远离后拱顶变形幅度逐渐减缓。
4)盾壳-土体之间的摩擦力对既有隧道拱顶位移的影响,主要存在于新建隧道开挖面附近,当开挖面离开后,对既有隧道造成影响的主要因素为土体损失。
本文在研究过程中存在一些简化,因为新建隧道与土体之间存在摩擦力,而摩擦力不在本次研究的范围内,所以未采用前期的试验数据(x=-6 m)进行分析。实际工程中盾构隧道开挖还涉及到刀盘推力、注浆压力等多因素的影响。此外,既有隧道模型选用聚乙烯PE圆管,与实际隧道结构模型相比存在一定简化,后续可在本文基础上进一步开展精细化研究。

