隧道穿越富水断层隔水岩体冲切剪切破坏研究

孙希波， 刘宏翔， 李鹏飞， *， 郭彩霞

(1. 北京市轨道交通建设管理有限公司， 北京 100068；2. 北京工业大学 城市与工程安全减灾教育部重点实验室， 北京 100124)

0 引言

随着我国隧道工程建设的迅猛发展，所面临的工程地质和水文地质环境日趋复杂，在修建过程中不可避免会遇到富水断层等不良地质情况。由于富水断层内岩体松散破碎，且通常具有高应力、高水压等特征，再加上施工管理不当等因素，施工过程中极易发生突水突泥灾害，对隧道建设及人员安全造成极大威胁[1]。为避免发生突水突泥灾害并为防突水措施的制定提供参考，研究隧道穿越富水断层时隔水岩体的最小安全厚度具有一定的工程应用价值。

国内外学者对隔水岩体最小安全厚度进行了相关研究，研究手段主要有理论分析和数值模拟。在理论分析方面： 1)有学者将极限平衡法应用于隔水岩体最小安全厚度的研究中，建立相应的力学模型，并针对力学模型进行受力分析得到力学平衡关系式，最后经过计算及化简得到隔水岩体最小安全厚度；此时，隔水岩体破坏形状为类长方体，在致灾构造的水、岩作用力下整体被冲进隧道临空面，为直接剪切破坏[2-7]。2)有学者则采用极限分析法，建立合理的、满足速度相容条件的破坏模式，根据几何关系确定隧道掌子面与致灾构造之间的隔水岩体破坏瞬时的内能耗散功率与各外力功率，令内能耗散功率等于各外力功率求解隔水岩体最小安全厚度；此时，隔水岩体破坏形状大多假定为圆锥墩台形，为冲切剪切破坏[8-15]。在数值模拟方面： 有限元法、有限差分法、离散元法等在隔水岩体最小安全厚度的研究中得到大量应用，在模拟过程中通常选取掌子面挤出变形、掌子面拱顶沉降、围岩纵向变形、塑性区分布作为指标来确定最小安全厚度的模拟解[16-22]。

上述研究中，对于隔水岩体最小安全厚度的理论分析方法大多以岩溶隧道为背景，以隧道穿越富水断层为背景的研究鲜有涉及；而针对隧道穿越富水断层时隔水岩体发生冲切剪切破坏的最小安全厚度研究更为少见。文献[7]与本文主题同为隧道穿越富水断层隔水岩体最小安全厚度问题，但其侧重点在于提出隔水岩体的直接剪切破坏模型，并未对隔水岩体发生冲切剪切破坏进行研究，且未进行相关的模拟分析。鉴于此，当隧道穿越富水断层时，本文提出隔水岩体冲切剪切破坏模式的力学模型，得到最小安全厚度的计算公式并进行影响因素分析，通过建立三维数值模型，确定最小安全厚度的模拟解，以验证理论解的合理性，最后将计算公式应用于实际工程以讨论其适用性。

1 隔水岩体冲切剪切破坏模式的力学模型及最小安全厚度推导计算

1.1 模型提出

既有研究针对隧道前方存在富水溶腔的情况提出了相对应的冲切剪切破坏模式的力学模型，其破坏形状大多为圆锥墩台形，如夏沅谱等[13]和王志杰等[14]的研究(分别见图1和图2)。笔者认为富水断层可看成具有倾角的大型富水溶腔，因此，隧道穿越断层的冲切剪切破坏模式可从隧道穿越富水溶腔的研究中得到参考。

图1 夏沅谱力学模型[13]

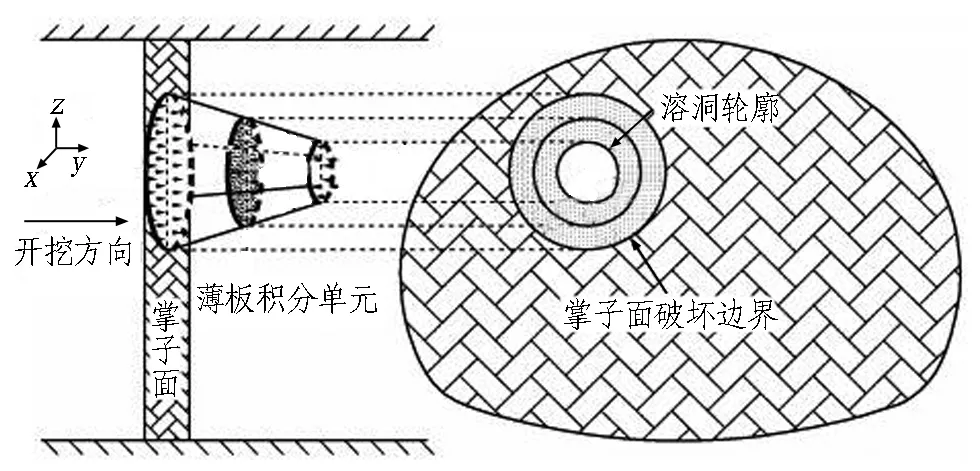
图2 王志杰力学模型[14]

当隧道前方存在富水断层时，建立隔水岩体冲切剪切破坏模式的力学模型，如图3所示。隔水岩体的破坏形状为锥底被部分截断的圆锥墩台形，其包含假设如下：

1)被截断的圆锥底面平行于断层倾角线，即当断层倾角发生变化时，隔水岩体破坏形状的轴线会随之变化；

2)圆锥体下侧的母线端点为掌子面底点，另一侧的母线过掌子面顶点，即圆锥体与掌子面的相交面为椭圆，且椭圆长轴上的2个端点分别为掌子面的顶点与底点；

3)圆锥轴线与母线的夹角为隔水岩体的内摩擦角φ；

4)断层及正常围岩岩体为理想弹塑性材料，满足摩尔-库仑屈服准则；

5)断层处作用力为均布压力，且不考虑断层水的劈裂作用。

隔水岩体最小安全厚度s为隧道掌子面中心点与正前方接触到断层时的直线距离。当隧道不断开挖掘进，直至掌子面与断层间的距离小于隔水岩体最小安全厚度时，即发生突水突泥，隔水岩体发生冲切剪切破坏，破坏体沿着冲切滑移面向隧道内运动，其速度方向与圆锥体轴线共线。

隔水岩体的冲切剪切破坏体为截圆锥墩台ABDE部分； d为圆锥体OCD的底面半径； L为被断层倾斜面所截的小圆锥体OAB的底面半径； R为隧道半径； θ为断层倾角； φ为隔水岩体的内摩擦角； s为最小安全厚度； σh+Q+G为断层作用力； σ、τ分别为冲切滑移面上的正应力及剪应力； GABDE为破坏体重力； v为破坏体的滑移速度。

1.2 最小安全厚度推导计算

1.2.1 面积和体积参数

如图3所示，根据几何关系，可得

(1)

圆锥体OCD与隧道掌子面相交面的面积

(2)

截圆锥体ODE的高

(3)

截圆锥体ODE的面积及体积为：

(4)

小圆锥体OAB的面积及体积为：

(5)

破坏体的面积

(6)

破坏体的体积

VABDE=VODE-VOAB=

(7)

1.2.2 力参数

在隔水岩体冲切剪切破坏模式的力学模型中，破坏体受到的外力为断层作用力(包括断层侧向地应力、水压力及断层处自重)及自身的重力，破坏体受到的内力为冲切滑移面上的正应力及剪应力。

断层作用力中侧向地应力的计算按照文献[7]的方法进行，由于本文提出的冲切剪切破坏模式的力学模型不考虑断层走向角，因此计算断层作用力时，走向角取0°代入，可得：

(8)

Q=ρwgh；

(9)

G=ρ1gbcosθ。

(10)

破坏体的重力为破坏体的密度ρ2、重力加速度g与破坏体体积的乘积，可得

GABDE=ρ2gVABDE。

(11)

因研究对象为深埋隧道，笔者认为隔水岩体的破坏体上方围岩能够形成稳定的普氏压力拱，故冲切滑移面上的正应力及剪应力采用普氏理论计算，由此可得：

(12)

τ=c+σtanφ。

(13)

式(12)—(13)中：σ为冲切面上的正应力，kPa；f为坚固因数，量纲为1，取f=Rc/10(Rc为岩体的单轴抗压强度，MPa)；τ为冲切面上的剪应力，kPa；ρ2为隔水岩体即正常围岩段的密度，t/m3；R为隧道半径，m；φ为隔水岩体的内摩擦角，(°)；c为隔水岩体的黏聚力，kPa。

1.2.3 隔水岩体最小安全厚度求解

本节基于极限分析法上限定理推导隔水岩体最小安全厚度的计算公式。

1)计算外力功率。在提出的力学模型中，外力包括断层作用力和破坏体重力。其中，断层作用力按假设为均布压力，属于面积力，且作用力方向与速度方向一致，均为圆锥体轴线方向，其功率可表示为

Wp=(σh+Q+G)πL2v。

(14)

破坏体重力属于体积力，且重力方向与速度方向存在夹角θ，重力做功功率

Wγ=ρ2gVABDEvcosθ。

(15)

总外力做功功率

We=Wp+Wγ。

(16)

破坏区域内能耗散率

Wv=(τvcosφ+σvsinφ)SABDE。

(17)

2)根据极限分析法上限定理，隔水岩体不发生破坏的条件是：

We≤Wv。

(18)

将式(6)—(17)代入式(18)中，经过化简可以得到基于极限分析法上限定理的关于参数L的一元三次方程：

iL3+jL2+k=0。

(19)

其中：

(20)

采用Matlab软件，并结合式(19)、(20)，可求解出关于参数L的一元三次方程，从而得到参数L的值。

3)根据力学模型中的几何关系，可得到隔水岩体最小安全厚度的计算表达式为：

(21)

2 最小安全厚度影响因素分析

由式(21)可知，隔水岩体发生冲切剪切破坏的最小安全厚度的影响因素为断层长度、宽度、倾角，隧道半径，水头高度和隔水岩体的内摩擦角、黏聚力等参数。为探究这些因素对最小安全厚度产生的影响，本节给出了冲切剪切破坏模式的隔水岩体最小安全厚度与各因素的变化关系曲线。

进行影响因素分析时，采用控制变量法，具体取值如下： 断层长度为500 m，宽度为60 m，倾角为60°，埋深为300 m，水头高度为180 m，隧道半径为6 m，隔水岩体内摩擦角为28°，黏聚力为300 kPa。其余参数如下： 断层处岩体取Ⅴ级围岩，根据《铁路隧道设计规范》确定，密度取1.84×103kg/m3；断层两侧正常围岩取Ⅳ级围岩，密度取2.14×103kg/m3；断层岩体与正常围岩接触面摩擦因数μ取0.1；侧压力系数K取1.2。

2.1 断层规模

断层规模包括断层的长度和宽度。当断层长度l=400～1 100 m、断层宽度b=50～120 m时，利用式(21)计算冲切剪切破坏模式隔水岩体最小安全厚度的理论值，并得到最小安全厚度与断层规模的关系曲线，如图4所示。可以看出，随着断层长度的增大，最小安全厚度增大幅度很小，几乎可以忽略；在断层宽度因素影响下，最小安全厚度呈现出随断层宽度的增大而不断增大、增大幅度越来越小的趋势。

(a) 断层长度影响曲线

(b) 断层宽度影响曲线

2.2 断层倾角

当断层倾角θ=30°～80°时，利用式(21)计算冲切剪切破坏模式隔水岩体最小安全厚度的理论值，并得到最小安全厚度与断层倾角的关系曲线，如图5所示。可以看出，随着断层倾角的增大，最小安全厚度刚开始呈现出较为明显的减小趋势，而当倾角大于40°以后，最小安全厚度的减小幅度很小，几乎可忽略。

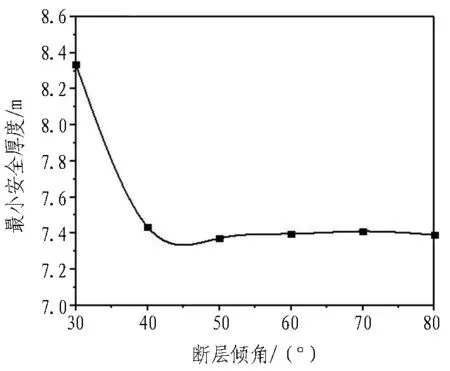
图5 最小安全厚度与断层倾角关系曲线

2.3 隧道半径及水头高度

当隧道半径R=5～12 m、水头高度h=140～280 m时，利用式(21)计算冲切剪切破坏模式隔水岩体最小安全厚度的理论值，并得到最小安全厚度与隧道半径及水头高度的关系曲线，分别如图6和图7所示。可以看出，最小安全厚度与隧道半径、水头高度均表现出明显的正相关性，且最小安全厚度受隧道半径影响的敏感性更强。

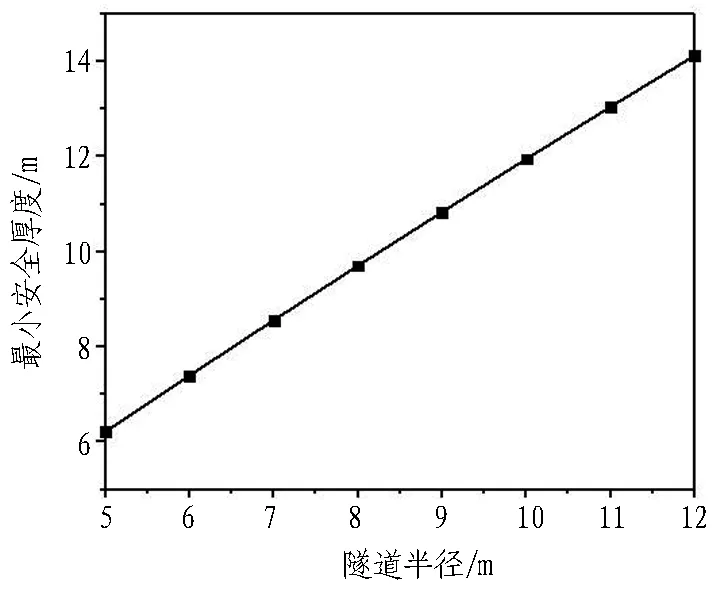
图6 最小安全厚度与隧道半径关系曲线

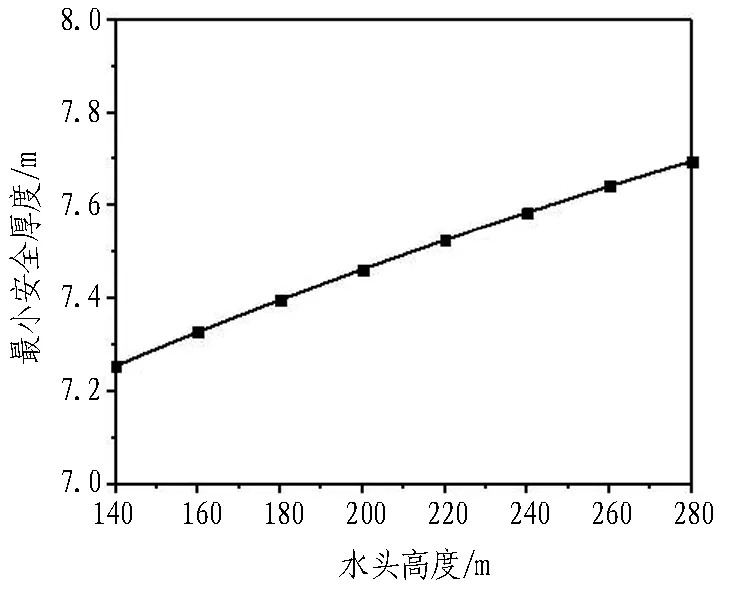
图7 最小安全厚度与水头高度关系曲线

2.4 隔水岩体的抗剪强度参数

隔水岩体抗剪强度参数包括隔水岩体的内摩擦角和黏聚力。当隔水岩体内摩擦角φ=20°～55°、黏聚力c=200～1 600 kPa时，利用式(21)计算冲切剪切破坏模式隔水岩体最小安全厚度的理论值，并得到最小安全厚度与隔水岩体抗剪强度参数的关系曲线，如图8所示。可以看出，随着隔水岩体内摩擦角和黏聚力的增大，最小安全厚度不断减小，且减小幅度越来越小。

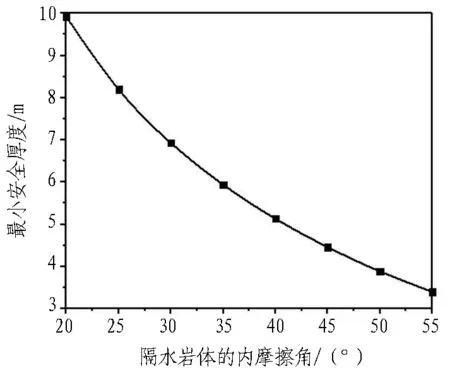
(a) 内摩擦角影响曲线

(b) 黏聚力影响曲线

3 最小安全厚度数值模拟研究

3.1 模型参数

采用有限差分软件FLAC3D建立隧道穿越富水断层的三维数值模型，如图9所示。隧道与断层的相对位置关系如图10所示。模型在X轴方向取100 m，Y轴方向取150 m，Z轴方向取152 m。隧道为马蹄形断开，横截面宽15 m、高12 m，隧道由左向右开挖；断层为富水断层，宽度为60 m，倾角为60°，倾向与隧道掘进方向同向。模型四周及下部边界为法向约束，上部边界为自由边界。

本次模拟中，隧道穿越断层处的隧道埋深约为150 m，隧道上方水头高度约为120 m。断层为富水断层，在模拟时认为水只存在于断层内部，断层两侧的正常围岩处于无水环境。断层处岩体取Ⅴ级围岩，断层两侧正常围岩取Ⅳ级围岩，具体的物理力学指标如表1所示。

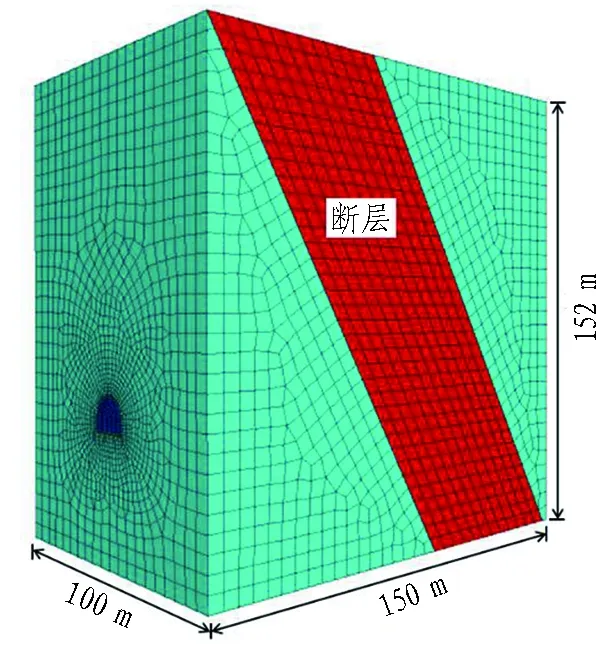
图9 三维数值模型

图10 隧道与断层的相对位置关系

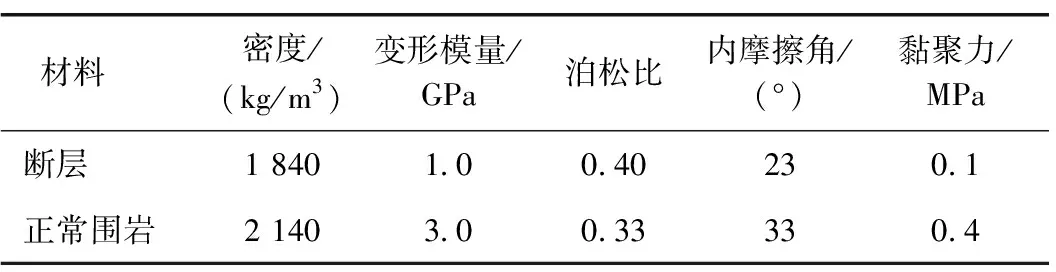
表1 物理力学指标

3.2 最小安全厚度模拟解的确定

模拟采用全断面开挖，且隧道朝断层掘进时采取不同的开挖进尺： 当隧道掌子面距断层较远时，每步开挖2 m；当隧道开挖至距断层10 m处时，每步开挖1 m，并以掌子面拱顶触及到断层为最终开挖步。根据既有数值模拟研究方法，选取掌子面挤出变形和塑性区分布作为指标来确定隧道穿越富水断层的隔水岩体最小安全厚度。

3.2.1 掌子面挤出变形

记录模型在不同开挖步下的掌子面挤出变形值，得到掌子面挤出变形随开挖步的变化曲线，如图11所示。可以看出： 当掌子面距断层位置较远时，挤出变形的变化较为稳定；而随着隧道不断开挖掘进，掌子面向断层靠近，挤出变形明显增大。

横坐标距断层0 m表示隧道已揭露断层。

表2示出不同开挖步下掌子面挤出变形的具体数值以及2个连续开挖步间的割线斜率。当某开挖步的割线斜率较先前有显著提高时，说明该开挖步下的挤出变形较先前显著增大，从而确定出隔水岩体的最小安全厚度。以掌子面距断层9 m处的割线斜率0.30为基准，当掌子面距断层4 m时，割线斜率为2.01，较基准提高了570%；而当掌子面距断层3 m时，割线斜率为3.17，较基准提高了960%。由此说明，掌子面距断层3 m时，割线斜率有较为显著的增大，认为在该开挖步下隔水岩体将抵挡不住断层处的作用力，容易发生突水突泥灾害。由于本文所定义的隔水岩体最小安全厚度是隧道掌子面中心点与正前方接触到断层时的直线距离，而本模拟中隧道揭露断层是掌子面拱顶处触及断层，按照定义，隔水岩体最小安全厚度应为模拟值3 m再加上受断层倾角影响的岩体距离l′=R/tanθ=[(15+12)/4]/tan 60°=3.90 m，最终确定隔水岩体最小安全厚度为6.90 m。

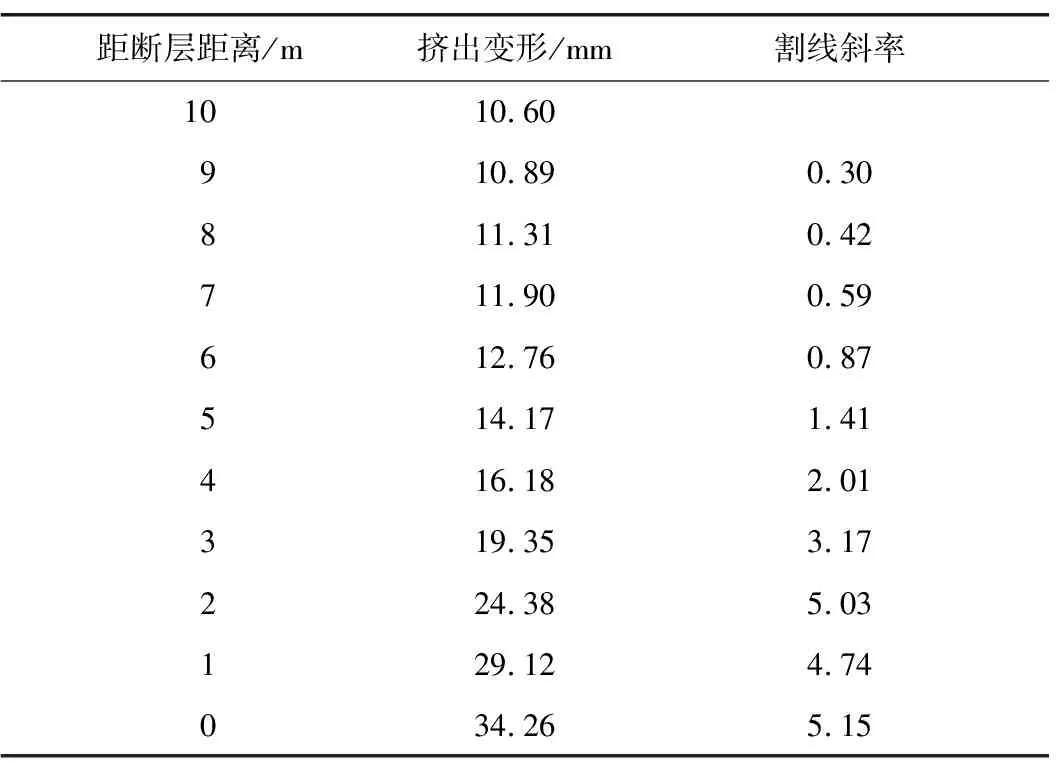
表2 掌子面挤出变形及割线斜率

图12为掌子面开挖临近断层处的位移矢量图。可以看出，当隧道开挖临近断层时，掌子面附近围岩的移动态势是朝向掌子面内侧运动，且移动态势较强的围岩主要位于隧道掌子面的斜前方。结合本文提出的隔水岩体冲切剪切破坏模型，模拟结果与理论模型所假定的破坏体位于隧道掌子面斜前方且向隧道内运动取得了较好的一致性，证明了冲切剪切理论模型具有一定的合理性。

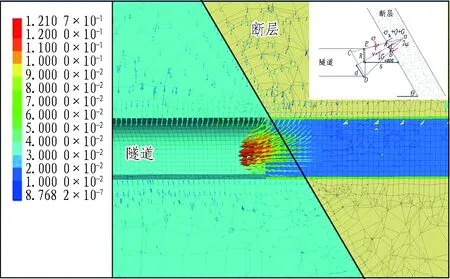
图12 掌子面开挖临近断层处的位移矢量图(单位: m)

3.2.2 塑性区分布

记录模型在不同开挖步下的塑性区分布云图，如图13所示。图中黑色倾斜线代表断层的倾斜面，以该线为界，左侧为正常围岩，右侧为断层。当开挖步进行到距断层3 m时，掌子面前方塑性区与断层相连，极可能诱发突水灾害，此时隔水岩体最小安全厚度为模拟值再加上受断层倾角影响的岩体距离，最终确定为6.90 m。

3.3 模拟解与理论解对比

根据掌子面挤出变形和塑性区分布指标，最终确定隔水岩体最小安全厚度的模拟解为6.90 m。为进行模拟解与理论解的对比，将模拟采用工程信息的相关参数(正常围岩的内摩擦角φ为33°，黏聚力c为400 kPa；隧道断面简化为圆形，半径R取6.75 m)代入式(21)，得到隔水岩体最小安全厚度的理论解为6.15 m。可以得知： 模拟解6.90 m与冲切剪切破坏计算模型的理论解6.15 m较为接近，模拟解与理论解吻合程度较高。

(a) 距断层5 m

(b) 距断层4 m

(c) 距断层3 m

(d) 距断层2 m

4 工程应用

永莲隧道是吉莲高速公路的控制性工程，隧址区地质构造发育，隧道出口段以砂岩、页岩及灰岩为主，次生构造较为发育。隧道左侧200 m左右发育1条大断裂，基本与隧道轴线平行。受该断裂影响，隧道发育有F1—F4共4条次生断裂带，其中，F2断层破碎带对隧道影响最显著。永莲隧道地质剖面图见图14。F2断层倾向E，倾角为84°，宽度为15～35 m，查明延伸长度为520 m，断层破碎带物质泥化后主要呈流塑状态，可看成Ⅵ级围岩。永莲隧道为双向分离式隧道，隧道开挖断面高度为9.06 m，宽度为12.6 m，隧道平均埋深180 m，地下水位距离隧道拱顶约150 m，隧道进口施工至揭露F2断层时发生大规模突水突泥灾害。

根据永莲隧道的工程信息，将其计算参数和隧道几何尺寸进行整理，如表3所示。此外，隧道断面简化为圆形，隧道半径R为5.4 m；摩擦因数μ取0.1，侧压力系数K取1.2。

图14 永莲隧道地质剖面图

表3 计算参数

将上述参数分别代入式(21)，可以得到冲切剪切破坏模式隔水岩体最小安全厚度值，并与既有研究的计算结果进行对比，如表4所示。

表4 隔水岩体最小安全厚度计算结果对比

由表4可以看出，在永莲隧道工程背景下，本文提出的冲切剪切破坏模型所得到的计算结果与既有研究处于同一量级；而且，本文计算方法得到的最小安全厚度较大，安全富余度更高。在永莲隧道的实际施工中，当隧道开挖临近F2断层时，由于未采取相关措施而导致了突水突泥灾害的发生。今后若有类似工程，可采用本文计算方法确定最小安全厚度，从而提前采取措施以避免突水突泥灾害。

5 结论与展望

本文提出了隧道穿越富水断层时隔水岩体冲切剪切破坏的力学计算模型，分析了断层规模、断层倾角、隧道半径、水头高度、隔水岩体抗剪强度参数等因素对理论解的影响，通过掌子面挤出变形和塑性区分布指标确定了最小安全厚度的模拟解，并与理论解进行对比，最后将计算公式应用于永莲隧道工程，取得的主要结论如下：

1)隔水岩体最小安全厚度随断层宽度、隧道半径、水头高度的增大而增大，随断层倾角、隔水岩体内摩擦角及黏聚力的增大而减小，随断层长度的变化则不明显。

2)最小安全厚度的模拟解与理论解较为吻合，且模拟得到，开挖临近断层时具有较强运动态势的围岩主要位于掌子面斜前方且朝向隧道内侧运动，与理论模型的假定一致。

3)经工程案例应用表明，冲切剪切破坏模型计算公式可作为预测隧道穿越富水断层时隔水岩体最小安全厚度的有效方法之一。

4)本文假定隔水岩体的冲切剪切破坏形状仅通过数值模拟进行了验证，下一步可通过模型试验及实际工程现场监测对隔水岩体的破坏形状进行修正。